Der Hauptsatz der Mineralogie

0.1
E: Der Haupsatz der Mineralogie
Satz: In einem Kristall gibt es nur 1,2,3,4 und 6-zählige Symmetrien.
Definition: Seien ~u, ~v 6= ~0 zwei Vektoren, die nicht auf einer Geraden liegen. Die Menge
G := { p · ~u + q · ~v | p, q ∈ Z}
heißt Gitter.
Satz: Die Vektoren ~u =
u1
u2
und ~v =
v1
v2
liegen genau dann nicht auf einer Geragen,
wenn gilt:
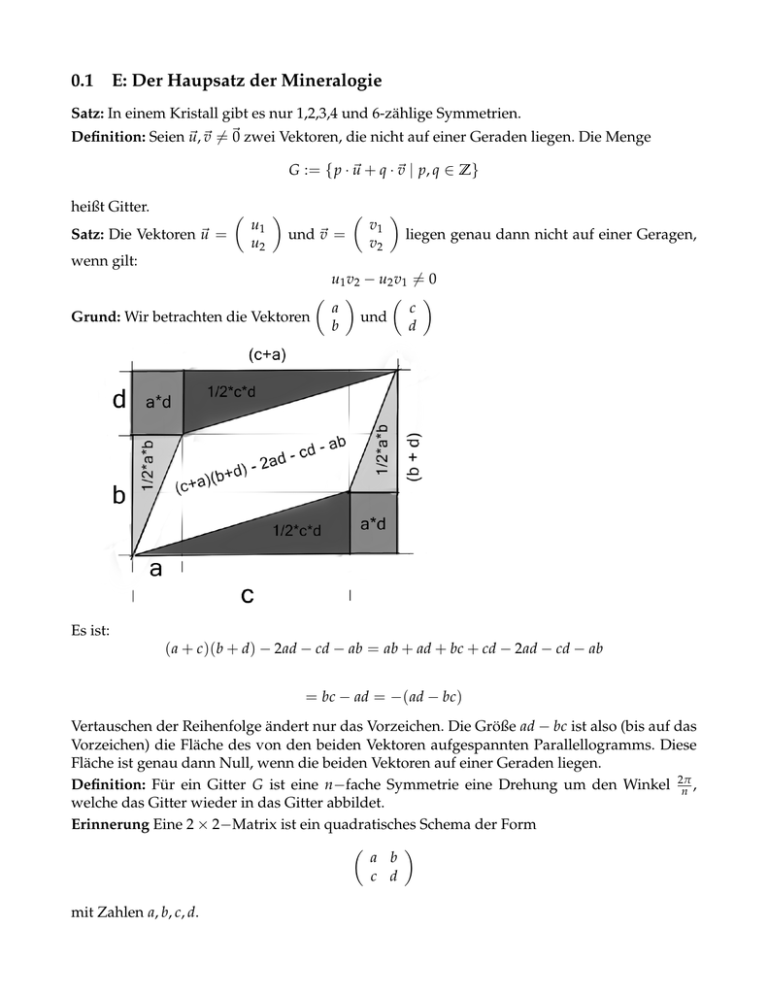
Grund: Wir betrachten die Vektoren
u1 v2 − u2 v1 6 = 0
a
c
und
b
d
Es ist:
( a + c)(b + d) − 2ad − cd − ab = ab + ad + bc + cd − 2ad − cd − ab
= bc − ad = −( ad − bc)
Vertauschen der Reihenfolge ändert nur das Vorzeichen. Die Größe ad − bc ist also (bis auf das
Vorzeichen) die Fläche des von den beiden Vektoren aufgespannten Parallellogramms. Diese
Fläche ist genau dann Null, wenn die beiden Vektoren auf einer Geraden liegen.
Definition: Für ein Gitter G ist eine n−fache Symmetrie eine Drehung um den Winkel 2π
n ,
welche das Gitter wieder in das Gitter abbildet.
Erinnerung Eine 2 × 2−Matrix ist ein quadratisches Schema der Form
a b
c d
mit Zahlen a, b, c, d.
Die Matrix-Vektor-Multiplikation is definiert durch:
a b
x
ax + by
·
=
c d
y
cx + dy
Ist B = (~b1 |~b2 ) die Matrix, die aus den Spalten ~b1 und ~b2 besteht, so ist die Matrix-MatrixMultiplikation definiert als:
A · B = A · (~b1 |~b2 ) := ( A · ~b1 | A · ~b2 )
Die Matrix-Matrix-Multiplikation ist assoziativ und das Neutralement der Matrix-Matrix-Multiplikation
ist
E2 =
1 0
0 1
Das Inverse einer Matrix A (bzgl. Matrix-Matrix-Multiplikation) wird (falls es existiert) mit A−1
bezeichnet. Es ist
−1
1
d −b
a b
=
c d
ad − bc −c a
falls ad − bc 6= 0.
Erinnerung: Die folgende Matrix D ϕ dreht einen Vektor ~x =
x
y
um den Winkel ϕ gegen
den Uhrzeigersinn
Dϕ =
Grund: Sei ~x =
Dann ist:
x
y
=r
cos(ψ)
sin(ψ)
cos( ϕ) − sin( ϕ)
sin( ϕ) cos( ϕ)
(Polarkoordinaten)
cos(ψ)
D ϕ · ~x = r
·
sin(ψ)
cos( ϕ) cos(ψ) − sin( ϕ) sin(ψ)
cos( ϕ + ψ)
=r
=r
sin( ϕ) cos(ψ) + cos( ϕ) sin(ψ)
sin( ϕ + ψ)
cos( ϕ) − sin( ϕ)
sin( ϕ) cos( ϕ)
(die letzte Gleichung sind die Additionstheoreme für sin und cos)
1
Offenbar gilt: D− ϕ = D −
ϕ .
Die Spur eine Matrix ist definiert als:
a b
Spur(
) = a+d
c d
Es gilt : Spur( AB) =Spur( BA), denn
Spur(
a b
c d
e f
·
) = ae + bg + c f + dh
g h
Spur(
e f
g h
a b
·
) = ea + f c + gb + hd
c d
Beispiel:
1 0
0 2
1 1
0 1
1 1
0 1
1 0
0 2
1 1
0 2
1 2
0 2
=
=
aber die Spuren der beiden Matrizen sind gleich.
Definition Eine Drehsymmetrie eines Gitters ist eine Drehung, die Gitterpunkte wieder auf das
Gitter abbildet.
Es muß also für eine Drehsymmetrie des Gitters gelten: Für alle p, q ∈ Z gibt es r, s ∈ Z, mit:
D ϕ ( p~u + q~v) = r~u + s~v
Ist ~u =
u1
u2
und ~v =
v1
v2
, so muß es ri , si ∈ Z geben, mit
D ϕ~u = r1~u + s1~v
D ϕ~v = r2~u + s2~v
Für zwei Vektoren ~a und ~b sei (~a|~b) die Matrix mit den Spalten ~a und ~b.
Das obige ist gleichbedeutend mit:
r1 u1 + s1 v1 r2 u1 + s2 v1
u1 v1
r1 r2
D ϕ (~u|~v) = (r1~u + s1~v|r2~u + s2~v) =
=
r1 u2 + s1 v2 r2 u2 + s2 v2
u2 v2
s1 s2
also
Dϕ
u1 v1
u2 v2
=
u1 v1
u2 v2
r1 r2
s1 s2
Multiplizieren wir den ersten und den letzten Ausdruck von links mit
u1 v1
u2 v2
−1
ten wir:
1
u1 v2 − v1 u2
Nun gilt mit A :=
v2 − v1
− u2 u1
u1 v1
u1 v2
cos ϕ − sin ϕ
u1 v1
r1 r2
·
=
sin ϕ cos ϕ
u2 v2
s1 s2
:
Spur A−1 · D ϕ · A
= Spur D ϕ · A · A−1
, so erhal-
= Spur
Aber die Spur der Matrix
r1 r2
s1 s2
cos ϕ
sin ϕ
− sin ϕ
cos ϕ
= 2 cos ϕ
ist r1 + s2 ∈ Z, also ganzzahlig. Die Frage ist also, wann
2 cos ϕ ganzzahlig ist.
Da gilt
−1 ≤ cos φ ≤ 1
ist
−2 ≤ 2 cos φ ≤ 2
Die ganzen Zahlen in diesem Bereich sind:
2 cos ϕ ∈ {−2, −1, 0, 1, 2}
Wir benötigen also die Winkel für cos φ ∈ {0, ± 21 , ±1}. Dabei interessieren wir uns nur für die
Winkel ϕ ∈ [0, π ].
π
Für n > 6 ist 2π
n < 3 . Da der Kosinus im Bereich [0, π ] streng monoton fallend ist, gilt:
cos(
π
2π
1
) > cos
=
n
3
2
insgesamt also:
1
< cos
2
2π
n
<1
Tabellarisch gilt für n:
360
n
cos 2π
n
n
1
360
1
2
180
−1
3
120
− 12
4
90
0
5
73
≈ 0.31
1
6
60
2
n > 6 < 60
> 21
Bemerkung zur genauen Konstruktion der Winkel:
Zum Punkt (1, 0) gibt es genau einen Punkt ( x0 , y0 ). der auf dem Einheitskreis oberhalb der
x −Achse liegt und vom Punkt (1, 0) den Abstand 1 hat. Diese beiden Punkte bilden, zusammen
mit dem Ursprung ein gleichseitiges Dreieck der Seitenlänge 1. Also halbiert die Projektion des
Punktes auf die x −Achse das Intervall [0, 1]. Somit gilt x0 = cos(φ) = 12 .
Der Punkt (− 12 , y0 ) hat vom Punkt ( x0 , y0 ) ebenfalls den Abstand 1. Es gilt (− 21 − 12 )2 + (y0 −
y0 )2 = 1. Wir haben also in den oberen Halbkreis drei solche Dreiecken eingeschrieben, was für
π
den Vollkreis sechs Dreiecke bedeutet. Der Winkel ϕ ist also 2π
6 = 3 (6-fache Symmetrie) .
Eine ähnlich Konstruktion vom Punkt (−1, 0) aus liefert für cos ϕ = − 21 den Winkel ϕ =
(3-fache Symmetrie) .
2π
3
3π
cos( ϕ) = 0 liefert die Winkel π2 = 2π
4 (4-fache Symmetrie) und φ = 2 (zu groß).
cos(φ) = ±1 gibt noch die Winkel φ = 0 und φ = π (2-fache Symmetrie).
Die Unmöglichkeit für n = 5 erhalt man aus
2π
2π
2π
<
<
6
5
4
und der Monotonie des Kosinus:
π
π
1
2π
cos
= > cos
> cos
=0
3
2
5
2