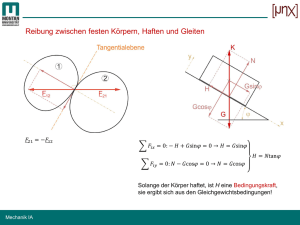
Ballon Von einem Freiballon aus werden die Orte A und B, die

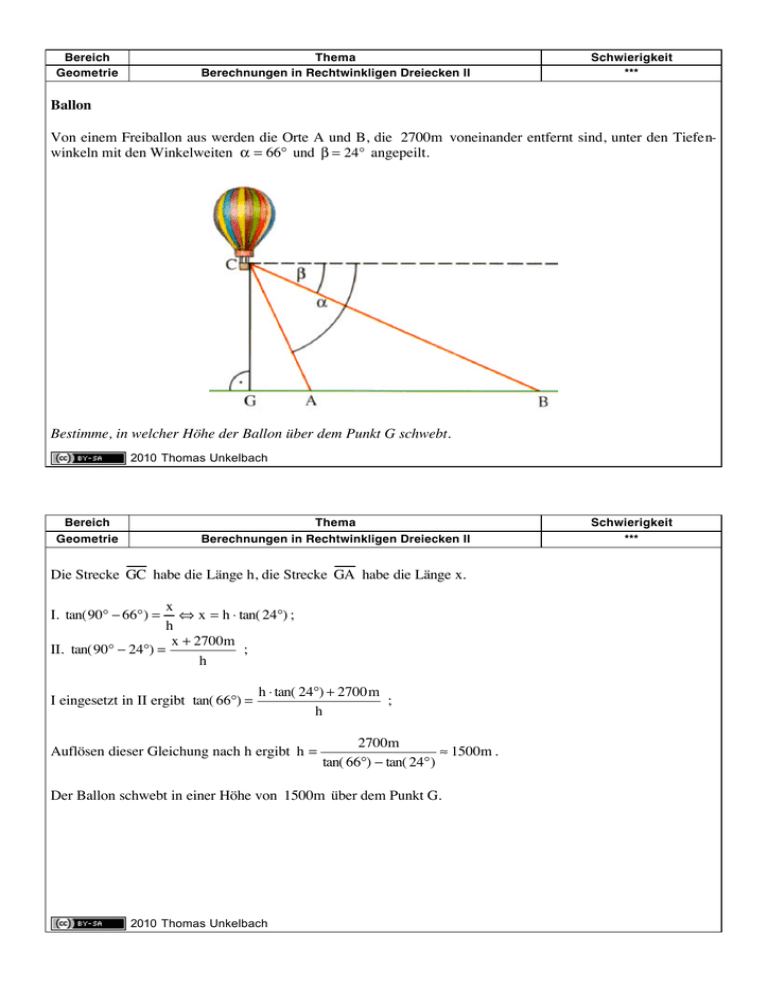
Bereich
Geometrie
Thema
Berechnungen in Rechtwinkligen Dreiecken II
Schwierigkeit
***
Ballon
Von einem Freiballon aus werden die Orte A und B, die 2700m voneinander entfernt sind, unter den Tiefenwinkeln mit den Winkelweiten α = 66° und β = 24° angepeilt.
Bestimme, in welcher Höhe der Ballon über dem Punkt G schwebt.
2010 Thomas Unkelbach
Bereich
Geometrie
Thema
Berechnungen in Rechtwinkligen Dreiecken II
Die Strecke GC habe die Länge h, die Strecke GA habe die Länge x.
x
⇔ x = h ⋅ tan( 24°) ;
h
x + 2700m
II. tan( 90° − 24°) =
;
h
I. tan( 90° − 66° ) =
I eingesetzt in II ergibt tan( 66°) =
h ⋅ tan( 24°) + 2700 m
;
h
Auflösen dieser Gleichung nach h ergibt h =
2700m
≈ 1500m .
tan( 66°) − tan( 24° )
Der Ballon schwebt in einer Höhe von 1500m über dem Punkt G.
2010 Thomas Unkelbach
Schwierigkeit
***
Bereich
Geometrie
Thema
Berechnungen in Rechtwinkligen Dreiecken II
Schwierigkeit
**
Baum
Treffen die Sonnenstrahlen unter einem
Winkel von 30° auf den Boden, so wirft ein
Baum einen 45m langen Schatten.
Bestimme, wie hoch der Baum ist.
2010 Thomas Unkelbach
Bereich
Geometrie
Thema
Berechnungen in Rechtwinkligen Dreiecken II
Die Höhe des Baums sei h.
tan( 30° ) =
h
⇔ h = 45m ⋅ tan( 30°) ; h ≈ 26m .
45m
Der Baum ist ungefähr 26m hoch.
2010 Thomas Unkelbach
Schwierigkeit
**
Bereich
Geometrie
Thema
Berechnungen in Rechtwinkligen Dreiecken II
Schwierigkeit
*
Baustelle 1
Die Handwerkskammer schreibt für Leitern einen Anstellwinkel von ca. 70° vor. Leitern über 7 m Länge müssen zusätzlich abgestützt werden.
Bestimme, wie hoch eine ordnungsgemäß aufgestellte Leiter, die 6m lang ist, an einer Wand hoch reicht.
2010 Thomas Unkelbach
Bereich
Geometrie
Thema
Berechnungen in Rechtwinkligen Dreiecken II
Die Höhe, die die Leiter an der Wand hoch reicht, sei h.
sin( 70° ) =
h
⇔ h = 6m ⋅ sin( 70°) ; h ≈ 5,64m .
6m
Die Leiter reicht 5,64m an der Wand hoch.
2010 Thomas Unkelbach
Schwierigkeit
*
Bereich
Geometrie
Thema
Berechnungen in Rechtwinkligen Dreiecken II
Schwierigkeit
*
Baustelle 2
Die Handwerkskammer schreibt für Leitern einen Anstellwinkel von ca. 70° vor. Leitern über 7 m Länge müssen zusätzlich abgestützt werden.
Bestimme, wie weit eine ordnungsgemäß aufgestellte Leiter, die 6m lang ist, von der Wand entfernt auf dem
Boden steht.
2010 Thomas Unkelbach
Bereich
Geometrie
Thema
Berechnungen in Rechtwinkligen Dreiecken II
Die Strecke, die die Leiter von der Wand entfernt auf dem Boden steht, sei s.
cos( 70°) =
s
⇔ s = 6 m ⋅ cos( 70°) ; s ≈ 2,05m .
6m
Die Leiter steht 2,05m von der Wand entfernt auf dem Boden.
2010 Thomas Unkelbach
Schwierigkeit
*
Bereich
Geometrie
Thema
Berechnungen in Rechtwinkligen Dreiecken II
Schwierigkeit
*
Baustelle 3
Die Handwerkskammer schreibt für Leitern einen Anstellwinkel von ca. 70° vor. Leitern über 7 m Länge müssen zusätzlich abgestützt werden.
Bestimme, wie lang eine ordnungsgemäß aufgestellte Leiter sein muss, um 15m an einer Wand hoch zu reichen.
2010 Thomas Unkelbach
Bereich
Geometrie
Thema
Berechnungen in Rechtwinkligen Dreiecken II
Die Länge der Leiter sei l .
sin( 70°) =
15m
15m
⇔l=
; l ≈ 16 m .
l
sin( 70°)
Die Leiter muss 16m lang sein.
2010 Thomas Unkelbach
Schwierigkeit
*
Bereich
Geometrie
Thema
Berechnungen in Rechtwinkligen Dreiecken II
Schwierigkeit
*
Brückenrampe
Geplant ist der Bau einer Brücke, die in 50m Höhe über einen Fluss führen soll. Die Zufahrt muss in Uferhöhe
liegen und darf höchstens unter einem Winkel von 3° ansteigen.
Bestimme, wie lang die Zufahrt mindestens sein muss.
2010 Thomas Unkelbach
Bereich
Geometrie
Thema
Berechnungen in Rechtwinkligen Dreiecken II
Die Länge der Zufahrt sei l .
sin( 3°) =
50m
50m
⇔l=
; l ≈ 955m .
l
sin( 3°)
Die Zufahrt muss 955m lang sein.
2010 Thomas Unkelbach
Schwierigkeit
*
Bereich
Geometrie
Thema
Berechnungen in Rechtwinkligen Dreiecken II
Schwierigkeit
***
Fabrik
Von einer 40 m langen ‚Standlinie’ AB , die auf einen Fabrikschornstein zuläuft, wird dessen Spitze mit einem
Thodoliten angepeilt. Die Höhenwinkel bei A und B haben die Winkelweiten α = 38° und β = 56° .
Bestimme die Höhe des Schornsteins.
2010 Thomas Unkelbach
Bereich
Geometrie
Thema
Berechnungen in Rechtwinkligen Dreiecken II
Schwierigkeit
***
Die Höhe des Schornsteins sei h, die Strecke vom Punkt B zum Lotfußpunkt der Schornsteinspitze habe die
Länge x.
h
;
40m + x
h
h
II. tan( 56° ) = ⇔ x =
;
x
tan( 56°)
I. tan( 38°) =
II eingesetzt in I ergibt tan( 38° ) =
h
h
40 m +
tan( 56°)
Auflösen dieser Gleichung nach h ergibt h =
Der Schornstein ist 66m hoch.
2010 Thomas Unkelbach
;
40 m ⋅ tan( 38°)
≈ 66m .
tan( 38°)
1−
tan( 56°)
Bereich
Geometrie
Thema
Berechnungen in Rechtwinkligen Dreiecken II
Schwierigkeit
**
Flugrichtung 1
Geschwindigkeiten stellt man in der Physik
durch Pfeile dar, Geschwindigkeiten mit verschiedenen Richtungen setzt man zusammen,
indem man aus den Geschwindigkeitspfeilen
Dreiecke bildet. Das nebenstehende Bild zeigt,
wie die Eigengeschwindigkeit des Flugzeuges


v e und die Windgeschwindigkeit v W sich zur

Geschwindigkeit v B überlagern, die die Bewegung des Flugzeuges über den Boden angibt. α
ist der „Kompasskurs“ des Flugzeuges.
Ein Pilot steuert den Kompasskurs 90° , das
Flugzeug hat die Eigengeschwindigkeit
360km / h , die Windgeschwindigkeit beträgt
60km / h .
Bestimme, um welchen Winkel das Flugzeug
von seinem Kurs abgelenkt wird.
2010 Thomas Unkelbach
Bereich
Geometrie
Thema
Berechnungen in Rechtwinkligen Dreiecken II
Die Weite des gesuchten Winkels sei ϕ .
tan(ϕ ) =
60km / h 1
= ⇒ ϕ ≈ 9,5° .
360km / h 6
Das Flugzeug wird um einen Winkel der Weite 9,5° von seinem Kurs abgelenkt.
2010 Thomas Unkelbach
Schwierigkeit
**
Bereich
Geometrie
Thema
Berechnungen in Rechtwinkligen Dreiecken II
Schwierigkeit
***
Flugrichtung 2
Geschwindigkeiten stellt man in der Physik
durch Pfeile dar, Geschwindigkeiten mit verschiedenen Richtungen setzt man zusammen,
indem man aus den Geschwindigkeitspfeilen
Dreiecke bildet. Das nebenstehende Bild zeigt,
wie die Eigengeschwindigkeit des Flugzeuges
r
r
v e und die Windgeschwindigkeit v W sich zur
r
Geschwindigkeit v B überlagern, die die Bewegung des Flugzeuges über den Boden angibt. α
ist der „Kompasskurs“ des Flugzeuges.
Ein Pilot möchte genau Richtung Osten fliegen
und steuert den Kompasskurs 80° . Die Windgeschwindigkeit beträgt 60km / h .
Bestimme, mit welcher Eigengeschwindigkeit
das Flugzeug fliegt, wenn es genau Richtung
Osten fliegt.
2010 Thomas Unkelbach
Bereich
Geometrie
Thema
Berechnungen in Rechtwinkligen Dreiecken II
Die Eigengeschwindigkeit des Flugzeugs sei v e .
sin( 90° − 80°) =
60 km / h
60km / h
⇒ ve =
; v e = 346 km / h .
ve
sin( 10°)
Das Flugzeug fliegt mit einer Eigengeschwindigkeit von 346km / h .
2010 Thomas Unkelbach
Schwierigkeit
***
Bereich
Geometrie
Thema
Berechnungen in Rechtwinkligen Dreiecken II
Schwierigkeit
***
Flugrichtung 3
Geschwindigkeiten stellt man in der Physik
durch Pfeile dar, Geschwindigkeiten mit verschiedenen Richtungen setzt man zusammen,
indem man aus den Geschwindigkeitspfeilen
Dreiecke bildet. Das nebenstehende Bild zeigt,
wie die Eigengeschwindigkeit des Flugzeuges
r
r
v e und die Wind geschwindigkeit v W sich zur
r
Geschwindigkeit v B überlagern, die die Bewegung des Flugzeuges über den Boden angibt. α
ist der „Kompasskurs“ des Flugzeuges.
Ein Flugzeug hat die Eigengeschwindigkeit
420 km / h , die Windgeschwindigkeit beträgt
40 km / h .
Bestimme, welchen Kompasskurs der Pilot
steuern muss, damit das Flugzeug genau Richtung Osten fliegt.
2010 Thomas Unkelbach
Bereich
Geometrie
Thema
Berechnungen in Rechtwinkligen Dreiecken II
Der Kompasskurs des Flugzeuges habe die Weite α .
sin( 90° − α) =
40 km / h
⇒ 90° − α ≈ 5,5° ⇒ α ≈ 84,5° .
420 km / h
Der Pilot muss den Kompasskurs 84,5° steuern.
2010 Thomas Unkelbach
Schwierigkeit
***
Bereich
Geometrie
Thema
Berechnungen in Rechtwinkligen Dreiecken II
Schwierigkeit
**
Flugzeugstart
Ein Flugzeug hebt mit einer Geschwindigkeit von 55m/s (Meter pro Sekunde) und einem Winkel von 34° vom
Boden ab.
Bestimme, in welcher Höhe sich das
Flugzeug nach 6 Sekunden befindet,
wenn es weiterhin mit der oben angegebenen Geschwindigkeit fliegt und
welche Strecke es in dieser Zeit über
den Boden überflogen hat.
2010 Thomas Unkelbach
Bereich
Geometrie
Thema
Berechnungen in Rechtwinkligen Dreiecken II
Schwierigkeit
**
Die Höhe des Flugzeugs nach 6 Sekunden sei h, die dabei über den Boden zurückgelegte Strecke habe die Lä nge s.
sin( 34°) =
h
⇔ h = 330 m ⋅ sin( 34°) ; h ≈ 185m .
6s ⋅ 55m / s
cos( 34°) =
s
⇔ s = 330 m ⋅ cos(34° ) ; s ≈ 275m .
6s ⋅ 55m / s
Das Flugzeug ist nach 6 s in einer Höhe von 185m und hat in dieser Zeit über den Boden 275m überflogen.
2010 Thomas Unkelbach
Bereich
Geometrie
Thema
Berechnungen in Rechtwinkligen Dreiecken II
Schwierigkeit
***
Flussbreite
Um die Breite eines Flusses zu bestimmen werden von einem Turm aus die beiden Flussufer unter den Tiefe nwinkeln mit den Weiten α = 42° und β = 29° angepeilt.
Bestimme die Breite des Flusses.
2010 Thomas Unkelbach
Bereich
Geometrie
Thema
Berechnungen in Rechtwinkligen Dreiecken II
Schwierigkeit
***
Die Breite des Flusses sei b, die Strecke vom Lotfußpunkt der rechten Turmspitze zum linken Flussufer habe
die Länge x.
x+b
;
46m
x
II. tan( 90° − 42°) =
⇔ x = 46m ⋅ tan( 48°) ;
46m
I. tan( 90° − 29°) =
II eingesetzt in I ergibt tan( 61°) =
46m ⋅ tan( 48°) + b
;
46 m
Auflösen dieser Gleichung nach b ergibt b = 46m ⋅ (tan(61 °) - tan(48 °)) ≈ 32m .
Der Fluss ist 32m breit.
2010 Thomas Unkelbach
Bereich
Geometrie
Thema
Berechnungen in Rechtwinkligen Dreiecken II
Schwierigkeit
**
Flussüberquerung 1
Geschwindigkeiten stellt man in der Physik durch
Pfeile dar, Geschwindigkeiten mit verschiedenen
Richtungen setzt man zusammen, indem man aus
den Geschwindigkeitspfeilen Dreiecke bildet.
Das nebenstehende Bild zeigt, wie die Eigenger
schwindigkeit des Bootes v e und die Strömungsr
geschwindigkeit v W sich zur Geschwindigkeit
r
v B überlagern, die die Bewegung des Bootes
über den Boden angibt. α ist der „Kompasskurs“
des Bootes.
Ein Kapitän steuert den Kompasskurs 90° , das
Boot hat die Eigengeschwindigkeit 36km / h , die
Strömungsgeschwindigkeit des Wassers beträgt
12km / h .
Bestimme, um welchen Winkel das Boot von seinem Kurs abgelenkt wird.
2010 Thomas Unkelbach
Bereich
Geometrie
Thema
Berechnungen in Rechtwinkligen Dreiecken II
Die Weite des gesuchten Winkels sei ϕ .
tan( ϕ) =
12km / h
⇒ ϕ ≈ 18, 4° .
36 km / h
Das Boot wird um einen Winkel der Weite 18,4° von seinem Kurs abgelenkt.
2010 Thomas Unkelbach
Schwierigkeit
**
Bereich
Geometrie
Thema
Berechnungen in Rechtwinkligen Dreiecken II
Schwierigkeit
***
Flussüberquerung 2
Geschwindigkeiten stellt man in der Physik
durch Pfeile dar, Geschwindigkeiten mit verschiedenen Richtungen setzt man zusammen,
indem man aus den Geschwindigkeitspfeilen
Dreiecke bildet. Das nebenstehende Bild zeigt,
r
wie die Eigengeschwindigkeit des Bootes v e und
r
die Strömungsgeschwindigkeit v W sich zur Ger
schwindigkeit v B überlagern, die die Bewegung
des Bootes über den Boden angibt. α ist der
„Kompasskurs“ des Bootes.
Ein Kapitän möchte das gegenüberliegende Ufer
im Punkt B erreichen und steuert den Kompasskurs 60° . Die Strömungsgeschwindigkeit des
Wassers beträgt 12km / h .
Bestimme, mit welcher Eigengeschwindigkeit das
Boot fahren muss, damit es das gegenüberliegende Ufer im Punkt B erreicht.
2010 Thomas Unkelbach
Bereich
Geometrie
Thema
Berechnungen in Rechtwinkligen Dreiecken II
Die Eigengeschwindigkeit des Bootes sei v e .
sin( 90° − 60°) =
12km / h
12km / h
⇒ ve =
; v e = 24km / h .
ve
sin( 30°)
Das Boot muss mit einer Eigengeschwindigkeit von 24 km / h fahren.
2010 Thomas Unkelbach
Schwierigkeit
***
Bereich
Geometrie
Thema
Berechnungen in Rechtwinkligen Dreiecken II
Schwierigkeit
***
Flussüberquerung 3
Geschwindigkeiten stellt man in der Physik durch
Pfeile dar, Geschwindigkeiten mit verschiedenen
Richtungen setzt man zusammen, indem man aus den
Geschwindigkeitspfeilen Dreiecke bildet. Das nebenstehende Bild zeigt, wie die Eigengeschwindigkeit
r
des Bootes v e und die Strömungsgeschwindigkeit
r
r
v W sich zur Geschwindigkeit v B überlagern, die die
Bewegung des Bootes über den Boden angibt. α ist
der „Kompasskurs“ des Bootes.
Ein Boot hat die Eigengeschwindigkeit 14km / h , die
Strömungsgeschwindigkeit des Wassers beträgt
12km / h .
Bestimme, welchen Kompasskurs der Kapitän steuern muss, damit das Boot das gegenüberliegende
Ufer im Punkt B erreicht.
2010 Thomas Unkelbach
Bereich
Geometrie
Thema
Berechnungen in Rechtwinkligen Dreiecken II
Der Kompasskurs des Bootes habe die Weite α .
sin( 90° − α) =
12km / h
⇒ 90° − α ≈ 59° ⇒ α ≈ 31° .
14km / h
Das Boot muss mit dem Kompasskurs 31° fahren.
2010 Thomas Unkelbach
Schwierigkeit
***
Bereich
Geometrie
Thema
Berechnungen in Rechtwinkligen Dreiecken II
Schwierigkeit
*
Gleichschenkliges Dreieck 1
In dem Gleichschenkligen Dreieck ABC ist b = 58,6m und
α = 62° .
Bestimme die Länge h der Höhe des Dreiecks.
2010 Thomas Unkelbach
Bereich
Geometrie
sin( 62°) =
Thema
Berechnungen in Rechtwinkligen Dreiecken II
h
⇔ h = 58,6m ⋅ sin( 62°) ; h ≈ 51,7 m .
58,6 m
2010 Thomas Unkelbach
Schwierigkeit
*
Bereich
Geometrie
Thema
Berechnungen in Rechtwinkligen Dreiecken II
Schwierigkeit
*
Gleichschenkliges Dreieck 2
In dem Gleichschenkligen Dreieck ABC ist a = 45,2m und
γ = 98° .
Bestimme die Länge h der Höhe des Dreiecks.
2010 Thomas Unkelbach
Bereich
Geometrie
cos( 12 ⋅ 98°) =
Thema
Berechnungen in Rechtwinkligen Dreiecken II
h
⇔ h = 45,2m ⋅ cos( 49° ) ; h ≈ 29,7 m .
45,2m
2010 Thomas Unkelbach
Schwierigkeit
*
Bereich
Geometrie
Thema
Berechnungen in Rechtwinkligen Dreiecken II
Schwierigkeit
*
Gleichschenkliges Dreieck 3
In dem Gleichschenkligen Dreieck ABC ist c = 124,8m und
β = 36° .
Bestimme die Länge h der Höhe des Dreiecks.
2010 Thomas Unkelbach
Bereich
Geometrie
tan( 36° ) =
Thema
Berechnungen in Rechtwinkligen Dreiecken II
1
2
h
⇔ h = 62, 4m ⋅ tan( 36° ) ; h ≈ 45,3m .
⋅124,8m
2010 Thomas Unkelbach
Schwierigkeit
*
Bereich
Geometrie
Thema
Berechnungen in Rechtwinkligen Dreiecken II
Schwierigkeit
*
Gleichschenkliges Dreieck 4
In dem Gleichschenkligen Dreieck ABC ist c = 9,76m und
γ = 79,5° .
Bestimme die Länge h der Höhe des Dreiecks.
2011 Thomas Unkelbach
Bereich
Geometrie
Thema
Berechnungen in Rechtwinkligen Dreiecken II
tan( 12 ⋅ 79,5°) =
1
2
⋅ 9,76 m
h
⇔h=
4,88m
; h ≈ 5,87 m .
tan( 39,75°)
2011 Thomas Unkelbach
Schwierigkeit
*
Bereich
Geometrie
Thema
Berechnungen in Rechtwinkligen Dreiecken II
Schwierigkeit
*
Gleichschenkliges Dreieck 5
In dem Gleichschenkligen Dreieck ABC ist a = 65,4m und
c = 54,7 m .
Bestimme die Winkelweite β und die Länge h der Höhe des
Dreiecks.
2010 Thomas Unkelbach
Bereich
Geometrie
cos(β) =
1
2
Thema
Berechnungen in Rechtwinkligen Dreiecken II
⋅ 54,7m
65,4m
sin( 65,3° ) =
⇒ β ≈ 65,3°
h
⇔ h = 65,4m ⋅ sin( 65,3°) ; h ≈ 59,4m .
65,4m
2010 Thomas Unkelbach
Schwierigkeit
*
Bereich
Geometrie
Thema
Berechnungen in Rechtwinkligen Dreiecken II
Schwierigkeit
*
Haus
Ein Haus erscheint aus der Entfernung 115m unter dem Höhenwinkel 32° .
Bestimme, wie hoch das Haus ist.
2010 Thomas Unkelbach
Bereich
Geometrie
Thema
Berechnungen in Rechtwinkligen Dreiecken II
Die Höhe des Hauses sei h.
tan( 32° ) =
h
⇔ h = 115m ⋅ tan( 32° ) ; h ≈ 72m .
115m
Das Haus ist 72m hoch.
2010 Thomas Unkelbach
Schwierigkeit
*
Bereich
Geometrie
Thema
Berechnungen in Rechtwinkligen Dreiecken II
Schwierigkeit
**
Höhe der Cheopspyramide
Die Cheopspyramide in Ägypten hat eine Seitenlänge von 230m. Wenn ein Be trachter 500m von der Pyramide
entfernt steht, sieht er die Spitze unter einem Winkel von 16° . Die Größe des Betrachters wird vernachlässigt.
Bestimme die Höhe der Cheopspyramide.
2010 Thomas Unkelbach
Bereich
Geometrie
Thema
Berechnungen in Rechtwinkligen Dreiecken II
Die Höhe der Cheopspyramide sei h.
tan(16°) =
h
⇔ h = 615m ⋅ tan( 16°) ; h ≈ 176m .
500m + 115m
Die Cheopspyramide ist 176m hoch.
2010 Thomas Unkelbach
Schwierigkeit
**
Bereich
Geometrie
Thema
Berechnungen in Rechtwinkligen Dreiecken II
Schwierigkeit
***
Kabel zur Insel
Vom Ufer aus soll
zum Punkt C auf einer
Insel in einem See ein
Kabel verlegt werden.
Dazu wurde am Ufer
eine
Strecke
von
100m abgemessen und
mit einem Vermessungsgerät der Punkt
C auf der Insel jeweils
von den Punkten A
und B angepeilt.
Bestimme den Abstand
des Punktes C vom
Ufer.
2010 Thomas Unkelbach
Bereich
Geometrie
Thema
Berechnungen in Rechtwinkligen Dreiecken II
Schwierigkeit
***
Zu berechnen ist der Abstand des Punktes C zur Strecke AB , d.h. die Höhe h des Dreiecks auf der Seite AB .
Seien p und q die beiden Teilstücke der Seite AB bis zum Lotfußpunkt der Höhe h.
h
h
⇔p=
;
p
tan( 66°)
h
h
II. tan( 45°) = ⇔ q =
;
q
tan( 45°)
I. tan( 66°) =
Wegen c = p + q gilt
100m =
h
h
1
1
+
= h ⋅(
+
)⇔h=
tan( 66° ) tan( 45° )
tan( 66°) tan( 45° )
Der Abstand des Punktes C vom Ufer beträgt 69m .
2010 Thomas Unkelbach
100 m
1
1
+
tan( 66°) tan( 45°)
; h ≈ 69m .
Bereich
Geometrie
Thema
Berechnungen in Rechtwinkligen Dreiecken II
Schwierigkeit
***
Kirchturm
Der Turmkopf einer Kirche
soll als Vermessungspunkt
dienen. Hierzu muss die Höhe
h bestimmt werden. Von den
Endpunkten einer auf den
Turmkopf
zulaufenden
‚Standlinie’
AB
mit
| AB | = 79,94m werden
die
Winkelweiten α = 25,24° und
β = 62,17° gemessen.
Bestimme die Höhe h.
2010 Thomas Unkelbach
Bereich
Geometrie
Thema
Berechnungen in Rechtwinkligen Dreiecken II
Die Strecke vom Punkt B zum Lotfußpunkt der Kirchturmspitze habe die Länge x.
h
;
79,94 m + x
h
h
II. tan( 62,17°) = ⇔ x =
;
x
tan( 62,17°)
I. tan( 25,24°) =
II eingesetzt in I ergibt tan( 25,24°) =
h
h
79,94m +
tan( 62,17° )
Auflösen dieser Gleichung nach h ergibt h =
Der Kirchturm ist 50,17m hoch.
2010 Thomas Unkelbach
;
79,94m ⋅ tan( 25,24°)
≈ 50,17m .
tan( 25,24° )
1−
tan( 62,17° )
Schwierigkeit
***
Bereich
Geometrie
Thema
Berechnungen in Rechtwinkligen Dreiecken II
Schwierigkeit
**
Kölner Dom
Die Türme des Kölner Doms sind 160m hoch. An einem
schönen Sommertag treffen die Sonnenstrahlen unter
einem Winkel der Weite 35° auf den Vorplatz.
Bestimme die Länge des Schattens, den die Türme des
Doms werfen.
2010 Thomas Unkelbach
Bereich
Geometrie
Thema
Berechnungen in Rechtwinkligen Dreiecken II
Die Länge des Schattens sei s.
tan( 35° ) =
160m
160m
⇔s=
; s ≈ 229m .
s
tan( 35°)
Die Türme werfen einen Schatten der Länge 229m.
2010 Thomas Unkelbach
Schwierigkeit
**
Klasse
10
Thema
Berechnung von rechtwinkligen Dreiecken
Schwierigkeit
*
Leiter
Eine 7,10m lange Leiter ist an einer hohen Wand so angelehnt, dass sie
am Boden 3,30m von der Wand entfernt ist.
Bestimme, wie hoch die Leiter an der Mauer reicht und wie der Winkel
zwischen der Leiter und dem Boden ist.
© 2007 Thomas Unkelbach; Quelle: unbekannt
Klasse
10
Thema
Berechnung von rechtwinkligen Dreiecken
Schwierigkeit
*
Die Höhe der Leiter an der Wand sei h.
<P>: h = (7,10m ) 2 − (3,30 m) 2 ≈ 6,30m .
cos( α) =
3,30 m
⇒ α ≈ 62° .
7,10m
Die Leiter steht 6,30m an der Hausmauer hoch. Der Winkel zwischen Leiter und Boden beträgt 62° .
© 2007 Thomas Unkelbach; Quelle: unbekannt
Bereich
Geometrie
Thema
Berechnungen in Rechtwinkligen Dreiecken II
Schwierigkeit
**
Leitungsmast
An einem schönen Sommertag treffen die Sonnenstrahlen unter einem
Winkel der Weite 75º auf den ebenen Boden auf. Ein Le itungsmast
wirft einen Schatten von 6m Länge.
Bestimme die Höhe des Leitungsmastes.
2010 Thomas Unkelbach
Bereich
Geometrie
Thema
Berechnungen in Rechtwinkligen Dreiecken II
Die Höhe des Leitungsmastes sei h.
tan( 75°) =
h
⇔ h = 6m ⋅ tan( 75°) ; h ≈ 22,4m .
6m
Die Höhe des Leitungsmastes beträgt 22,4m .
2010 Thomas Unkelbach
Schwierigkeit
**
Bereich
Geometrie
Thema
Berechnungen in Rechtwinkligen Dreiecken II
Schwierigkeit
***
Leuchttürme
Von zwei Leuchttürmen L1 und L2 ,
die 7km voneinander entfernt sind,
wird ein Schiff S angepeilt. Man
misst die Winkelweiten α 1 = 42°
und α 2 = 55 ° .
Bestimme die Entfernung des Schiffes
von der Küste.
2010 Thomas Unkelbach
Bereich
Geometrie
Thema
Berechnungen in Rechtwinkligen Dreiecken II
Schwierigkeit
***
Zu berechnen ist der Abstand des Punktes S zur Strecke L 1L 2 , d.h. die Höhe h des Dreiecks auf der Seite
L 1L 2 .
Seien p und q die beiden Teilstücke der Seite L 1L 2 bis zum Lotfußpunkt der Höhe h.
h
h
⇔p=
;
p
tan( 42°)
h
h
II. tan( 55° ) = ⇔ q =
;
q
tan( 55° )
I. tan( 42°) =
Wegen c = p + q gilt
7 km =
h
h
1
1
+
= h ⋅(
+
)⇔h =
tan( 42° ) tan( 55°)
tan( 42°) tan( 55°)
Das Schiff ist 3,87km von der Küste entfernt.
2010 Thomas Unkelbach
7 km
1
1
+
tan( 42° ) tan( 55°)
; h ≈ 3,87 km .
Bereich
Geometrie
Thema
Berechnungen in Rechtwinkligen Dreiecken II
Schwierigkeit
**
Lilienthal
Otto LILIENTHAL (1840-1896) war der erste fliegende Mensch. Er flog zum Beispiel mit einem Drachenflieger aus 25m Höhe ca. 185m weit.
Bestimme, in welchem Gleitwinkel LILIENTHAL geflogen ist.
2010 Thomas Unkelbach
Bereich
Geometrie
Thema
Berechnungen in Rechtwinkligen Dreiecken II
Der Gleitwinkel habe die Winkelweite α .
tan( α°) =
25m
⇒ α ≈ 7 ,7 ° .
185m
Der Gleitwinkel betrug 7,7° .
2010 Thomas Unkelbach
Schwierigkeit
**
Bereich
Geometrie
Thema
Berechnungen in Rechtwinkligen Dreiecken II
Schwierigkeit
***
Loreley
Von der Loreley, einem 132m über dem
Rhein liegenden Felsen, sieht man die
beiden Flussufer unter den Tiefenwinkeln
mit den Weiten α = 41,4° und β = 65,6° .
Bestimme die Breite des Rheins an dieser
Stelle.
2010 Thomas Unkelbach
Bereich
Geometrie
Thema
Berechnungen in Rechtwinkligen Dreiecken II
Schwierigkeit
***
Die Breite des Rheins sei b, die Strecke vom Lotfußpunkt der Loreley am Boden zum rechten Flussufer habe
die Länge x.
x+b
;
132m
x
II. tan( 90° − 65,6°) =
⇔ x = 132m ⋅ tan( 24,4°) ;
132m
I. tan( 90° − 41,4° ) =
II eingesetzt in I ergibt tan( 48,6°) =
132m ⋅ tan( 24,4° ) + b
;
132m
Auflösen dieser Gleichung nach b ergibt b = 132m ⋅ (tan(48,6 °) - tan(24,4 °)) ≈ 90m .
Der Rhein ist an dieser Stelle 90m breit.
2010 Thomas Unkelbach
Bereich
Geometrie
Thema
Berechnungen in Rechtwinkligen Dreiecken II
Schwierigkeit
*
Parallelogramm 1
In dem Parallelogramm
d = 10,0cm und α = 60° .
ABCD
ist
a = 8,0cm ,
Bestimme die Länge h a der Höhe des Parallelogramms
und dessen Flächeninhalt A .
2010 Thomas Unkelbach
Bereich
Geometrie
sin( 60°) =
Thema
Berechnungen in Rechtwinkligen Dreiecken II
ha
⇔ h a = 10,0cm ⋅ sin( 60°) ; h a ≈ 8,7 cm
10,0cm
A = a ⋅ h a = 8,0cm ⋅ 8,7cm = 69,6cm 2
2010 Thomas Unkelbach
Schwierigkeit
*
Bereich
Geometrie
Thema
Berechnungen in Rechtwinkligen Dreiecken II
Schwierigkeit
**
Parallelogramm 2
In dem Parallelogramm
b = 7,5cm und β = 125° .
ABCD
ist
a = 12,0cm ,
Bestimme die Länge h a der Höhe des Parallelogramms
und dessen Flächeninhalt A .
2010 Thomas Unkelbach
Bereich
Geometrie
Thema
Berechnungen in Rechtwinkligen Dreiecken II
sin( 180° − 125°) =
ha
⇔ h a = 7,5cm ⋅ sin( 55° ) ; h a ≈ 6,1cm
7,5cm
A = a ⋅ h a = 12,0cm ⋅ 6,1cm = 73, 2cm 2
2010 Thomas Unkelbach
Schwierigkeit
**
Bereich
Geometrie
Thema
Berechnungen in Rechtwinkligen Dreiecken II
Schwierigkeit
*
Prinzessin
Um die Prinzessin zu entführen, hat der Ritter die
4,50m lange Leiter unter einem ‚Höhenwinkel’
von 65° an die Burgmauer gelehnt.
Bestimme, wie hoch die Leiter an der Burgmauer
reicht.
2010 Thomas Unkelbach
Bereich
Geometrie
Thema
Berechnungen in Rechtwinkligen Dreiecken II
Die Höhe der Leiter an der Burgmauer sei h.
sin( 65°) =
h
⇔ h = 4,50m ⋅ sin( 65° ) ; h ≈ 4,08m .
4,50m
Die Leiter reicht 4,08m hoch.
2010 Thomas Unkelbach
Schwierigkeit
*
Bereich
Geometrie
Thema
Berechnungen in Rechtwinkligen Dreiecken II
Schwierigkeit
***
Pultdach
In der nebenstehenden Abbildung ist
ein sogenanntes ‚Pultdach’ gezeigt.
Die Bauordnung schreibt für die
Winkelweiten α und β folgende
Wertebereiche
vor:
0
0
0
0
65 ≤ α ≤ 80 und 35 ≤ β ≤ 45 .
Bestimme, wie hoch das Dach
mindestens und höchstens wird.
2010 Thomas Unkelbach
Bereich
Geometrie
Thema
Berechnungen in Rechtwinkligen Dreiecken II
Schwierigkeit
***
Zu berechnen ist der Abstand der Dachspitze zur Strecke AB , d.h. die Höhe h des Dreiecks auf der Seite AB .
Seien p und q die beiden Teilstücke der Seite AB bis zum Lotfußpunkt der Höhe h.
h
h
⇔p=
;
p
tan( 65°)
h
h
II. tan( 35° ) = ⇔ q =
;
q
tan( 35° )
I. tan( 65°) =
Wegen c = p + q gilt
6,50m =
h
h
1
1
+
= h ⋅(
+
)⇔h=
tan( 65°) tan( 35°)
tan( 65° ) tan( 35°)
Analog ergibt sich mit den beiden anderen Winkeln h ≈ 5,53m .
Das Dach wird mindestens 3,43m und höchstens 5,53m hoch.
2010 Thomas Unkelbach
6,50m
1
1
+
tan( 65° ) tan( 35°)
; h ≈ 3, 43m .
Bereich
Geometrie
Thema
Berechnungen in Rechtwinkligen Dreiecken II
Schwierigkeit
***
Rakete
Beim Start einer Rakete von Cap Canaveral konnte man von der Zuschauertribüne aus die 10m hohe Spitze der
Rakete unter den Höhenwinkeln mit den Winkelweiten α = 4,3° und β = 4,6° beobachten.
Bestimme die Höhe der Rakete und die Entfernung der Rakete von der Zuschauertribüne.
2010 Thomas Unkelbach
Bereich
Geometrie
Thema
Berechnungen in Rechtwinkligen Dreiecken II
Schwierigkeit
***
Die Höhe der Rakete sei h, die Strecke von der Zuschauertribüne zum Lotfußpunkt der Spitze der Rakete auf
den Boden habe die Länge s.
h − 10m
;
s
h
h
II. tan( 4,6°) = ⇔ s =
;
s
tan( 4,6°)
I. tan( 4,3° ) =
II eingesetzt in I ergibt tan( 4,3°) =
h − 10m
;
h
tan( 4,6° )
Auflösen dieser Gleichung nach h ergibt h =
Aus II folgt s =
10m
≈ 153m .
tan( 4,3°)
1−
tan( 4,6°)
h
≈ 1900 m .
tan( 4,6°)
Die Rakete ist 153m hoch und steht von der Zuschauertribüne 1900m entfernt.
2010 Thomas Unkelbach
Bereich
Geometrie
Thema
Berechnungen in Rechtwinkligen Dreiecken II
Schwierigkeit
***
Ruine
Von zwei Peilstäben in der Ebene aus wird die Spitze der Ruine auf dem Berg angepeilt.
Bestimme den Höhenunterschied zwischen der Ebene und der Spitze der Ruine.
2010 Thomas Unkelbach
Bereich
Geometrie
Thema
Berechnungen in Rechtwinkligen Dreiecken II
Schwierigkeit
***
Die Strecke von der Oberkante des rechten Peilstabs zum Lotfußpunkt der Ruine auf die Höhe 1,50m habe die
Länge x, der Höhenunterschied zwischen der Oberkante der Peilstäbe und der Spitze der Ruine sei h ' .
h'
;
80m + x
h'
h'
II. tan( 50 °) = ⇔ x =
;
x
tan( 50°)
I. tan( 30° ) =
II eingesetzt in I ergibt tan( 30° ) =
h'
h'
80m +
tan( 50° )
Auflösen dieser Gleichung nach h ' ergibt h ' =
;
80 m ⋅ tan( 30°)
≈ 89,60m .
tan( 30°)
1−
tan( 50°)
Damit liegt die Spitze der Ruine h = h '+1,50m ≈ 91,10m höher als die Ebene.
2010 Thomas Unkelbach
Bereich
Geometrie
Thema
Berechnungen in Rechtwinkligen Dreiecken II
Schwierigkeit
*
Schornstein
Ein Schornstein, der 75m hoch ist,
wirft einen 70m langen Schatten.
Bestimme die Weite des Winkels,
unter dem die Sonnenstrahlen auf den
ebenen Boden treffen.
2010 Thomas Unkelbach
Bereich
Geometrie
tan( β) =
Thema
Berechnungen in Rechtwinkligen Dreiecken II
75m
⇒ β ≈ 47° .
70m
Die Sonnenstrahlen treffen unter einem Winkel der Weite 47 ° auf den ebenen Boden.
2010 Thomas Unkelbach
Schwierigkeit
*
Bereich
Geometrie
Thema
Berechnungen in Rechtwinkligen Dreiecken II
Schwierigkeit
**
Schüttkegel
Beim Aufschütten von Salz, Getreide, Sand usw. entsteht ein Schüttkegel. Der Böschungswinkel (im Bild siehst
du den Böschungswinkel für Salz) ist bei den einzelnen Materialien verschieden.
Bestimme den Durchmesser eines 3m hohen Schüttkegel aus Salz.
2010 Thomas Unkelbach
Bereich
Geometrie
Thema
Berechnungen in Rechtwinkligen Dreiecken II
Der Durchmesser des Schüttkegels sei d.
tan( 34° ) =
3m
3m
⇔ d = 2⋅
; d ≈ 8,80m .
d/2
tan( 34°)
Der Durchmesser des Schüttkegels beträgt 8,80m .
2010 Thomas Unkelbach
Schwierigkeit
**
Bereich
Geometrie
Thema
Berechnungen in Rechtwinkligen Dreiecken II
Schwierigkeit
*
Segelflugzeug 1
Ein Segelflugzeug befindet sich in 1250m Höhe und ist noch 42 km von seinem Ziel entfernt.
Bestimme, wie groß der Gleitwinkel höchstens sein darf, damit das Segelflugzeug sein Ziel ohne Unterstützung
durch zusätzlichen Aufwind erreicht.
2010 Thomas Unkelbach
Bereich
Geometrie
tan( α°) =
Thema
Berechnungen in Rechtwinkligen Dreiecken II
1250 m
⇒ α ≈ 1,7° .
42000m
Der Gleitwinkel darf höchstens 1,7° betragen.
2010 Thomas Unkelbach
Schwierigkeit
*
Bereich
Geometrie
Thema
Berechnungen in Rechtwinkligen Dreiecken II
Schwierigkeit
*
Segelflugzeug 2
Ein Segelflugzeug befindet sich in 1250m Höhe, ist noch 42 km von seinem Ziel entfernt und fliegt mit einem
Gleitwinkel von 1,5° .
Bestimme, in welcher Höhe das Segelflugzeug das Ziel überfliegt, wenn es das Ziel ohne Unterstützung durch
zusätzlichen Aufwind erreicht.
2010 Thomas Unkelbach
Bereich
Geometrie
Thema
Berechnungen in Rechtwinkligen Dreiecken II
Die Höhe des Segelflugzeugs über dem Zielpunkt sei h.
tan(1,5° ) =
1250m − h
; h = 1250m − tan( 1,5°) ⋅ 42000m ; h ≈ 150m .
42000 m
Das Segelflugzeug überfliegt das Ziel in einer Höhe von 150m .
2010 Thomas Unkelbach
Schwierigkeit
*
Bereich
Geometrie
Thema
Berechnungen in Rechtwinkligen Dreiecken II
Schwierigkeit
**
Tanne
Eine Tanne ist 25m hoch und wirft einen Schatten von 30m Länge.
Bestimme die Weite des Winkels, unter dem die Sonnenstrahlen auf den ebenen Boden treffen.
2010 Thomas Unkelbach
Bereich
Geometrie
Thema
Berechnungen in Rechtwinkligen Dreiecken II
Die Weite des gesuchten Winkels sei α .
tan( α) =
25m
⇒ α ≈ 40° .
30m
Die Sonnenstrahlen treffen unter einem Winkel der Weite 40 ° auf den ebenen Boden.
2010 Thomas Unkelbach
Schwierigkeit
**
Bereich
Geometrie
Thema
Berechnungen in Rechtwinkligen Dreiecken II
Schwierigkeit
*
Turm
Die Höhe eines Turmes soll bestimmt werden. Dazu hat ein Vermessungsingenieur mit Hilfe eines Thodoliten
den Winkel bestimmt, unter dem ein Betrachter den Turm sieht.
Bestimme die Höhe des Turmes.
2010 Thomas Unkelbach
Bereich
Geometrie
Thema
Berechnungen in Rechtwinkligen Dreiecken II
Die Höhe des Turms sei h.
tan( 32° ) =
h − 1,8m
⇔ h = 50m ⋅ tan( 32°) + 1,8m ; h ≈ 33m .
50m
Der Turm ist 33m hoch.
2010 Thomas Unkelbach
Schwierigkeit
*
Bereich
Geometrie
Thema
Berechnungen in Rechtwinkligen Dreiecken II
Schwierigkeit
***
Turm am Fluss
Von der Spitze eines Turms aus werden zwei Punkte an den beiden Ufern eines Flusses, der 40m breit ist, unter den Tiefenwinkeln mit den Winkelweiten 65° und 28 ° angepeilt.
Bestimme, welche Höhe der Turm hat.
2010 Thomas Unkelbach
Bereich
Geometrie
Thema
Berechnungen in Rechtwinkligen Dreiecken II
Schwierigkeit
***
Der Turm habe die Höhe h, die Strecke vom Lotfußpunkt der Spitze des Turms zum linken Flussufer habe die
Länge x.
x
⇔ x = h ⋅ tan( 25°) ;
h
x + 40m
II. tan( 90° − 28°) =
;
h
I. tan( 90° − 65° ) =
I eingesetzt in II ergibt tan( 62°) =
h ⋅ tan( 25°) + 40 m
;
h
Auflösen dieser Gleichung nach h ergibt h =
Der Turm ist 28m hoch.
2010 Thomas Unkelbach
40m
≈ 28m .
tan( 62°) − tan( 25°)
Bereich
Geometrie
Thema
Berechnungen in Rechtwinkligen Dreiecken II
Schwierigkeit
***
Turm am See
Von der Spitze eines Turms aus werden zwei Punkte an den beiden Ufern eines Sees, der 40m breit ist, unter
den Tiefenwinkeln mit den Winkelweiten α = 65° und β = 28° angepeilt.
Bestimme, welche Höhe der Turm hat.
2010 Thomas Unkelbach
Bereich
Geometrie
Thema
Berechnungen in Rechtwinkligen Dreiecken II
Schwierigkeit
***
Der Turm habe die Höhe h, die Strecke vom Lotfußpunkt der Spitze des Turms zum linken Flussufer habe die
Länge x.
x
⇔ x = h ⋅ tan( 25°) ;
h
x + 40m
II. tan( 90° − 28°) =
;
h
I. tan( 90° − 65° ) =
I eingesetzt in II ergibt tan( 62°) =
h ⋅ tan( 25°) + 40 m
;
h
Auflösen dieser Gleichung nach h ergibt h =
Der Turm ist 28m hoch.
2010 Thomas Unkelbach
40m
≈ 28m .
tan( 62°) − tan( 25°)
Bereich
Geometrie
Thema
Berechnungen in Rechtwinkligen Dreiecken II
Schwierigkeit
***
Vermessung am Fluss
Um die Breite eines
Flusses zu bestimmen,
hat man an einem Ufer
eine Strecke S1S2 von
400m Länge abgesteckt und am anderen
Ufer einen Punkt P
durch
einen
Vermessungsstab
markiert. Man ermittelt
59° als Weite des
Winkels
S2 S1 P und
71° als Weite des
Winkels PS2 S1 .
Bestimme die Breite
des Flusses.
2010 Thomas Unkelbach
Bereich
Geometrie
Thema
Berechnungen in Rechtwinkligen Dreiecken II
Schwierigkeit
***
Zu berechnen ist der Abstand des Punktes P zur Strecke S1S2 , d.h. die Höhe h des Dreiecks auf der Seite S1S2 .
Seien p und q die beiden Teilstücke der Seite S1S2 bis zum Lotfußpunkt der Höhe h.
h
h
⇔p=
;
p
tan( 59° )
h
h
II. tan( 71°) = ⇔ q =
;
q
tan( 71°)
I. tan( 59° ) =
Wegen c = p + q gilt
400 m =
h
h
1
1
+
= h ⋅(
+
)⇔h=
tan( 59°) tan( 71°)
tan( 59°) tan( 71°)
Die Breite des Flusse beträgt 423m .
2010 Thomas Unkelbach
400m
1
1
+
tan( 59° ) tan( 71° )
; h ≈ 423m .