Vorkurs Mathematik 2016

Vorkurs Mathematik 2016
3. Potenzen und Potenzgesetze
Die einfachsten Potenzfunktionen ergeben sich für natürliche Exponenten:
f (x) = x n ,
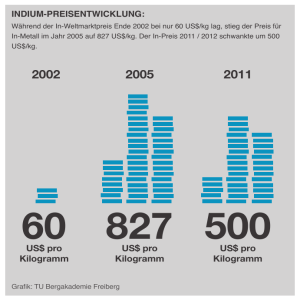
Abb. 1: Ungerade Exponenten
n 2 N.
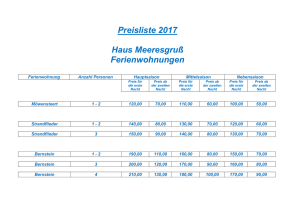
Abb. 2: Gerade Exponenten
Die Funktionen für die Exponenten n1 sind die Umkehrfunktionen zu x n .
TU Bergakademie Freiberg | Fakultät 1 | S. Bernstein, M. Helm, S. Dempe et al | Vorkurs Mathematik | 2016
1
3. Potenzen und Potenzgesetze
Definition 1.
Seien A und B Mengen. Eine Funktion f : A ! B ist eine Vorschrift, durch
die jedem x 2 A genau ein y = f (x) 2 B zugeordnet wird.
A heißt Definitionsbereich von f , B heißt Zielmenge von f , und
f (A) := {f (x) : x 2 A} µ B heißt Wertebereich oder Bild von f .
Zu einer gegebenen Menge A0 µ A heißt
f (A0 ) := {f (x) : x 2 A0 } µ B
das Bild von A0 unter f . Zu einer gegebenen Menge B 0 µ B heißt
f °1 (B 0 ) := {x 2 A : f (x) 2 B 0 }
das Urbild von B 0 unter f .
TU Bergakademie Freiberg | Fakultät 1 | S. Bernstein, M. Helm, S. Dempe et al | Vorkurs Mathematik | 2016
2
3. Potenzen und Potenzgesetze
Definition 2.
Eine Funktion f : A ! B heißt
injektiv (eineindeutig), wenn für alle x1 ,x2 2 A mit x1 6= x2 stets
f (x1 ) 6= f (x2 ) gilt,
surjektiv, wenn es zu jedem y 2 B ein x 2 A gibt mit y = f (x),
bijektiv, wenn f injektiv und surjektiv ist.
Ist f bijektiv, so existiert die Umkehrfunktion
f °1 : B ! A,
f °1 (y) = x :, y = f (x).
TU Bergakademie Freiberg | Fakultät 1 | S. Bernstein, M. Helm, S. Dempe et al | Vorkurs Mathematik | 2016
3
3. Potenzen und Potenzgesetze
Der Graph der Umkehrfunktion f °1 ergibt sich aus dem Graphen der
Funktion f durch Spiegeln an der Geraden y = x.
y = f (x) () f °1 (y) = f °1 (f (x)) = x
TU Bergakademie Freiberg | Fakultät 1 | S. Bernstein, M. Helm, S. Dempe et al | Vorkurs Mathematik | 2016
4
3. Potenzen und Potenzgesetze
p
p
3
Die gezeigten Wurzelfunktionen x 7! x und x 7! x sind die
Umkehrfunktionen von f (x) = x 2 und f (x) = x 3 mit den nichtnegativen
Zahlen als Definitionsbereich.
TU Bergakademie Freiberg | Fakultät 1 | S. Bernstein, M. Helm, S. Dempe et al | Vorkurs Mathematik | 2016
5
3. Potenzen und Potenzgesetze
Definition 3 (Wurzel).
Die n-te Wurzel, n 2 N, aus einer reellen Zahl a ∏ 0, ist diejenige p
nichtnegative reelle Zahl b, für die bn = a gilt. Man schreibt b = n a.
Die n-te Wurzel bzw. die Wurzelfunktion f (x) =
x ∏ 0 definiert.
p
n
x ist nur für nichtnegative
TU Bergakademie Freiberg | Fakultät 1 | S. Bernstein, M. Helm, S. Dempe et al | Vorkurs Mathematik | 2016
6
3. Potenzen und Potenzgesetze
Wurzel und Quadrat
Für beliebige reellen Zahlen x gilt
Somit hat die Gleichung x 2 = a
p
p
x2 =
q
x 2 = |x |.
im Fall a < 0 keine reelle Lösung,
(°x)2 =
q
im Fall a ∏ 0 zwei reelle Lösungen, nämlich x =
p
|x |2 und somit
p
p
a und x = ° a.
Achtung: Die Lösung x = ° a im zweiten Fall wird häufig vergessen!
TU Bergakademie Freiberg | Fakultät 1 | S. Bernstein, M. Helm, S. Dempe et al | Vorkurs Mathematik | 2016
7
3. Potenzen und Potenzgesetze
WO STECKT DER FEHLER?
p
8x 2 ° 4 ° 2x = 0.
Man bestimme alle Lösungen von
p
8x 2 ° 4 ° 2x = 0
(1)
p
8x 2 ° 4 = 2x
(2)
8x 2 ° 4 = 4x 2
(3)
4x 2 = 4
x2 = 1
Folglich sind 1 und °1 Lösungen der Gleichung
(4)
(5)
p
p
7x
= 0.= 0.
8x22° 3 °4 2x 2x
Art des Fehlers: (A) beide Lösungen sind falsch, (B) x = °1 ist keine Lösung,
(C) x = 1 ist keine Lösung, (D) es gibt keine Lösungen.
TU Bergakademie Freiberg | Fakultät 1 | S. Bernstein, M. Helm, S. Dempe et al | Vorkurs Mathematik | 2016
8
3. Potenzen und Potenzgesetze
Der lange Weg zu den Potenzgesetzen:
1. Schritt: x n , n 2 N, also eine natürliche Zahl (ungleich Null). Wie jeder
weiß, gilt:
106 · 103 = 10
· 10 · 10 · 10} · 10
| · 10 · 10{z
| · 10
{z · 10}
9
= 10
·
10
·
10
·
10
·
10
·
10
·
10
·
10
·
10
=
10
|
{z
}
6+3 = 9 Faktoren
Das gilt deshalb auch allgemein für jede reelle Zahl x 2 R und natürliche
Zahlen m,n 2 N
n+m
x n · x m = x| · x ...x
·
x
·
x
·
x
...x
·
x
=
x
·
x
...x
·
x
·
x
...x
·
x
=
x
{z } | {z } |
{z
}
n Faktoren
m Faktoren
n+m Faktoren
m
x
m
n
(mn)
sowie analog (x ) = x
und x n = x m°n , falls m > n.
TU Bergakademie Freiberg | Fakultät 1 | S. Bernstein, M. Helm, S. Dempe et al | Vorkurs Mathematik | 2016
9
3. Potenzen und Potenzgesetze
Rationale und reelle Exponenten
2. Schritt: Wir definieren zunächst x
1
n.
p
1
n
Die Umkehrfunktion zu x (x > 0) ist x n := n x. Sie erfüllt die Gleichung
≥ 1 ¥n
xn
= x.
Wegen der diskutierten Probleme mit der Umkehrfunktion bei geradem
Exponenten n definiert man x
1
n
nur für nichtnegative x.
Für positive rationale Exponenten definieren wir
x
m
n
≥
= x
1 ¥m
n
p
n
= ( x)m ,
x ∏ 0,
n,m 2 N.
3. Schritt: Per Definition ist x 0 = 1 für alle x 2 R.
TU Bergakademie Freiberg | Fakultät 1 | S. Bernstein, M. Helm, S. Dempe et al | Vorkurs Mathematik | 2016
10
3. Potenzen und Potenzgesetze
4. Schritt: Negative ganze Zahlen °n, n 2 N.
Für x 6= 0 gilt x · x1 = 1 und damit auch
µ ∂n
1
n
x ·
x
xn
1
n
=1= n =x n.
x
x
Deshalb definiert man x °n := x1n , und es gilt
m
x
x m · x °n = n = x m°n .
x
Ergebnis: Für rationale Zahlen r = m
n ist
x
m
n
p
n
= ( x)m .
Für irrationale Æ 2 R wird x Æ mittels Stetigkeitsargument definiert: Zu jeder
irrationalen Zahl Æ gibt es eine Folge rationaler Zahlen mit lim rn = Æ,
und wir definieren:
n!1
x Æ := lim x rn .
n!1
TU Bergakademie Freiberg | Fakultät 1 | S. Bernstein, M. Helm, S. Dempe et al | Vorkurs Mathematik | 2016
11
3. Potenzen und Potenzgesetze
Potenzgesetze
Für beliebige reelle Zahlen a, b, c 2 R und natürliche Zahlen n 2 N sowie
m 2 Z gelten die folgenden Potenzgesetze:
(ab )c = a(bc) ,
a > 0,
(ab)c = ac bc ,
a, b > 0,
ab+c = ab ac ,
a
°b
=
1
,
ab
b
a
ab°c = c ,
a
1
an
m
an
=
=
p
n
a,
p
n
a > 0,
a>0
a>0
a ∏ 0.
p
am = ( n a)m ,
a ∏ 0.
TU Bergakademie Freiberg | Fakultät 1 | S. Bernstein, M. Helm, S. Dempe et al | Vorkurs Mathematik | 2016
12
3. Potenzen und Potenzgesetze
Quadrieren und Potenzieren mit geradem Exponenten
Beispiel: Aus x = °3 folgt x 2 = (°3)2 = 9. Wenden wir das Wurzelziehen
als Umkehroperation an, so folgt
p
x 2 = |x | =
p
9 = 3,
und wir erhalten 2 Lösungen x1 = °3 und x2 = 3.
Merke: Quadrieren ist keine äquivalente Umformung!
Trotzdem wird man in vielen Fällen quadrieren, um eine Lösung zu
erhalten. In diesem Fall muss man eine Probe machen, um beim
Quadrieren entstandene Scheinlösungen zu identifizieren.
Das Phänomen tritt analog bei sämtlichen Potenzen mit geradem
Exponenten auf.
TU Bergakademie Freiberg | Fakultät 1 | S. Bernstein, M. Helm, S. Dempe et al | Vorkurs Mathematik | 2016
13
3. Potenzen und Potenzgesetze
Potenzieren mit ungeradem Exponenten
Beispiel: Die Gleichung x 3 = °8 besitzt
die einzige Lösung x = °2.
p
3
Allerdings darf diese nicht als x = °8 geschrieben werden, denn Wurzeln
sind nur für nichtnegative Zahlen definiert!
Die korrekten Schritte beim äquivalenten Umformen lauten hier
x 3 = °8 () °x 3 = 8 () (°x)3 = 8
() °x =
p
3
8 = 2 () x = °2.
Eine Probe ist entbehrlich, da äquivalent umgeformt wurde. Sie schadet
aber auch nicht.
TU Bergakademie Freiberg | Fakultät 1 | S. Bernstein, M. Helm, S. Dempe et al | Vorkurs Mathematik | 2016
14
3. Potenzen und Potenzgesetze
p
3
Exkurs: Warum nicht einfach °8 = °2?
Ein Grund wäre die Allgemeingültigkeit der Potenzgesetze: Es gilt für
m 2 Z, n, k 2 N:
x
m
n
=x
m ·k
n ·k
.
p
3
Würde man fälschlicherweise mit °2 = °8 rechnen, so folgt daraus ein
Widerspruch:
°2 =
p
3
1
°8 = (°8) 3
2
= (°8) 6
=
q
6
1· 2
= (°8) 3·2
(°8)2 =
p
6
64 = 2.
Eine weitere Begründung lernen Sie in HM 1 kennen: in den komplexen
Zahlen hat die Gleichung x 3 = °8 drei verschiedene Lösungen!
TU Bergakademie Freiberg | Fakultät 1 | S. Bernstein, M. Helm, S. Dempe et al | Vorkurs Mathematik | 2016
15
3. Potenzen und Potenzgesetze
Lösen von Potenzgleichungen
Die Gleichung x n = a mit geradem Exponenten n 2 N besitzt:
p
n
genau die beiden Lösungen x1/2 = ± a, falls a ∏ 0,
keine Lösung, falls a < 0.
Die Gleichung x n = a mit ungeradem Exponenten n 2 N besitzt:
die eindeutige Lösung x =
p
n
a, falls a ∏ 0,
p
p
n
die eindeutige Lösung x = ° |a| = ° n °a, falls a < 0.
TU Bergakademie Freiberg | Fakultät 1 | S. Bernstein, M. Helm, S. Dempe et al | Vorkurs Mathematik | 2016
16
3. Potenzen und Potenzgesetze
Lösungsverfahren für Wurzelgleichungen
1. Den maximalen Definitionsbereich bestimmen.
2. Quadrieren bzw. Potenzieren bis keine Wurzeln mehr auftreten.
3. Resultierende Gleichung lösen.
4. Abgleich der erhaltenen Lösungen mit dem Definitionsbereich.
5. Probe.
Lösen Sie die beiden Wurzelgleichungen
p
p
x °1+ x +2 = 1
und
p
4
p
x3 +4 = x +2
TU Bergakademie Freiberg | Fakultät 1 | S. Bernstein, M. Helm, S. Dempe et al | Vorkurs Mathematik | 2016
17
3. Potenzen und Potenzgesetze
Die Gleichung
besitzt keine Lösung.
p
p
x °1+ x +2 = 1
TU Bergakademie Freiberg | Fakultät 1 | S. Bernstein, M. Helm, S. Dempe et al | Vorkurs Mathematik | 2016
18
3. Potenzen und Potenzgesetze
Die Gleichung
p
4
x3 +4 =
besitzt die Lösungen x0 = 0, x1 =
p
1° 17
2
p
x +2
und x2 =
p
1+ 17
2
.
TU Bergakademie Freiberg | Fakultät 1 | S. Bernstein, M. Helm, S. Dempe et al | Vorkurs Mathematik | 2016
19
3. Potenzen und Potenzgesetze
Die Exponentialfunktion x 7! ax ist für a > 0 und alle x 2 R definiert.
Gebräuchliche Werte für die Basis sind die Zahlen 10, 2 und e º 2.71828.
TU Bergakademie Freiberg | Fakultät 1 | S. Bernstein, M. Helm, S. Dempe et al | Vorkurs Mathematik | 2016
20
3. Potenzen und Potenzgesetze
Plot von Exponentialfunktionen zu verschiedenen Basen:
TU Bergakademie Freiberg | Fakultät 1 | S. Bernstein, M. Helm, S. Dempe et al | Vorkurs Mathematik | 2016
21
3. Potenzen und Potenzgesetze
Die Eulersche Zahl e
Ein Startkapital von 1e werde jeweils für ein Jahr angelegt. Auf Leonhard
Euler (1707-1783) geht folgende Überlegung zum Zinseszins zurück:
Bei jährlicher Verzinsung mit 100% sind am Jahresende 2e fällig.
Bei halbjährlicher Verzinsung mit 50% sind am Jahresende (1 + 12 )2 e
= 2.25e zu zahlen.
Bei vierteljährlicher Verzinsung mit 25% sind am Jahresende (1 + 14 )4 e
º 2.44e zu zahlen.
1 -tel des
Frage: Wie wächst die zu zahlende Summe, wenn 100
%
pro
n
n
Jahres zu zahlen sind? Wird diese Zahl beliebig groß?
Euler: Nein, denn
µ
1
e := lim 1 +
n!1
n
∂n
º 2.71828.
TU Bergakademie Freiberg | Fakultät 1 | S. Bernstein, M. Helm, S. Dempe et al | Vorkurs Mathematik | 2016
22
3. Potenzen und Potenzgesetze
Exponential- und Logarithmusfunktion
Die Logarithmusfunktion ist die Umkehrfunktion der Eponentialfunktion.
Der Definitionsbereich der Logarithmusfunktion ist das offene Intervall
(0; 1). Der Logarithmus ist folglich nur für positive Argumente x definiert.
Für die Basis a gilt a > 0.
TU Bergakademie Freiberg | Fakultät 1 | S. Bernstein, M. Helm, S. Dempe et al | Vorkurs Mathematik | 2016
23
3. Potenzen und Potenzgesetze
Wozu braucht man den Logarithmus?
Schallpegel
(dB)
120
90
60
30
0
Schallintensität
(W/m2)
Düsenjet in 500m Entfernung
Rock-Konzert
U-Bahn
PKW
leise Unterhaltung
ruhiges Zimmer
Blätterrauschen
Hörbarkeitsgrenze
1
10-3
Wie laut ist laut?
10-6
10-9
10-12
Die Schallintensität I läuft von I0 = 10°12 W2 bis über 100 = 1 W2 , deshalb
m
m
ist eine logarithmische Darstellung als Schallpegel P besser:
I
P = 10log10 .
I0
TU Bergakademie Freiberg | Fakultät 1 | S. Bernstein, M. Helm, S. Dempe et al | Vorkurs Mathematik | 2016
24
3. Potenzen und Potenzgesetze
Rechnen mit Logarithmen
Alle Logarithmengesetze ergeben sich aus den Potenzgesetzen.
Für x,y > 0 und a > 0, a 6= 1 sowie r ,b > 0 gilt
b = loga c () ab = c,
ab = eb lna ,
loga (xy) = loga x + loga y,
loga x r = r loga x,
≥ ¥
loga yx = loga x ° loga y ,
loga x °r = loga x1r = ° loga x r = °r loga x,
wichtige Beziehungen: loga 1 = ln1 = 0,loga a = lne = 1.
log x
Umrechnungsformel: loga x = logb a und loga x = lnx
.
lna
b
TU Bergakademie Freiberg | Fakultät 1 | S. Bernstein, M. Helm, S. Dempe et al | Vorkurs Mathematik | 2016
25
3. Potenzen und Potenzgesetze
Logarithmen- und Exponentialgleichungen
Maximalen Definitionsbereich bestimmen.
Logarithmen- und Potenzgesetze anwenden und Gleichung lösen.
Liegt die Lösung im Definitionsbereich? (Betrifft vor allem
Logarithmen.)
Beispiel:
log10 (x ° 2) = 1
( () log10 (x ° 2) = log10 10)
=) x ° 2 = 10
() x = 12
Da x = 12 im Definitionsbereich liegt, ist x = 12 Lösung der Gleichung.
TU Bergakademie Freiberg | Fakultät 1 | S. Bernstein, M. Helm, S. Dempe et al | Vorkurs Mathematik | 2016
26
3. Potenzen und Potenzgesetze
Bestimmen Sie alle reellen Lösungen der Gleichung
1
lnx ° ln(3x ° 2) = 0.
2
TU Bergakademie Freiberg | Fakultät 1 | S. Bernstein, M. Helm, S. Dempe et al | Vorkurs Mathematik | 2016
27
3. Potenzen und Potenzgesetze
Beispiel zur Exponentialgleichung:
9x °1 = 36 · 3x
Maximaler Definitionsbereich: x 2 R.
Anwenden von Potenzgesetzen:
9x °1 = (32 )x °1 = 32(x °1)
und 36 · 3x = 36+x
ergibt
32(x °1) = 36+x
() 2(x ° 1) = 6 + x
| log3
() x = 8.
TU Bergakademie Freiberg | Fakultät 1 | S. Bernstein, M. Helm, S. Dempe et al | Vorkurs Mathematik | 2016
28
3. Potenzen und Potenzgesetze
Plot zum Beispiel 9x °1 = 36 · 3x mit x = 8 als Lösung:
TU Bergakademie Freiberg | Fakultät 1 | S. Bernstein, M. Helm, S. Dempe et al | Vorkurs Mathematik | 2016
29
3. Potenzen und Potenzgesetze
Bestimmen Sie alle reellen Lösungen der Gleichung
3x +3 ° 2 · 5x = 5x +1 + 2(3x + 5x ).
TU Bergakademie Freiberg | Fakultät 1 | S. Bernstein, M. Helm, S. Dempe et al | Vorkurs Mathematik | 2016
30