Aufgabe mit Lösung - Gottfried K. Weitbrecht

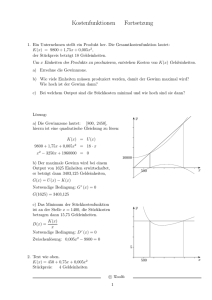
PRÜFUNG DER FACHHOCHSCHULREIFE
Nachprüfung
an Berufskollegs zum Erwerb der Fachhochschulreife u.a.
2007
Fach : M a t h e m a t i k
Aufgabe 7
Punkte
7.1
7.2
Der Betrieb A möchte für sein Produkt bei vollständiger Konkurrenz die
Gesamtkostenfunktion K in Abhängigkeit von der Ausbringungsmenge (in ME)
durch eine ganzrationale Funktion 3. Grades ermitteln.
Bekannt ist, dass sich die fixen Kosten auf 20 GE belaufen. Das Produkt wird
zu einem Stückpreis von 29 GE verkauft.
Bei einer Ausbringungsmenge von 2 ME besteht Kostendeckung. Minimale
variable Stückkosten entstehen bei einer Produktion von 5 ME und betragen
10 GE.
Bestimmen Sie die Gesamtkostenfunktion.
7
Gegeben sind die Gesamtkostenfunktion K und die Erlösfunktion E durch
K ( x ) = x 3 − 10 x 2 + 35 x + 20
E ( x ) = 29 x .
7.2.1 Zeichnen Sie die Graphen von K und E in ein geeignetes Koordinatensystem.
4
7.2.2 Markieren Sie die Gewinnzone. Geben Sie Nutzenschwelle und Nutzengrenze
an und erläutern Sie deren Bedeutung.
4
7.2.3 Welcher Mindestpreis muss gefordert werden, damit der Betrieb A seine
variablen Kosten decken kann?
4
Der Betrieb B bietet seine produzierte Ware als einzige Firma auf dem Markt an.
7.3.1 Die Gesamtkostenfunktion K und die Preis-Absatz-Funktion p von Betrieb B
sind angegeben durch
K ( x ) = x 3 − 10 x 2 + 35 x + 20
p( x ) = − 4 x + 40
0 ≤ x ≤ 10 .
Berechnen Sie den maximalen Gewinn und geben Sie den Cournotschen
Punkt an.
Wie lässt sich der Cournotsche Punkt zeichnerisch ermitteln?
8
7.3.2 Die Marktsituation führt zu einer Veränderung der Preis-Absatz-Funktion. Sie
wird wie folgt festgestellt:
p * ( x ) = − 4 x + 31,5
Prüfen Sie, ob der Betrieb B noch verlustfrei produzieren kann.
3
_____
30
PRÜFUNG DER FACHHOCHSCHULREIFE
Nachprüfung
an Berufskollegs zum Erwerb der Fachhochschulreife u.a.
2007
Fach : M a t h e m a t i k
Aufgabe 7 (Seite 1/2)
LÖSUNGSVORSCHLAG
7.1
Ansatz:
K ( x ) = ax 3 + bx 2 + cx + d und
kv ( x ) = ax 2 + bx + c ,
Bedingungen:
Punkte
E ( x ) = 29 x
2
kv ′ ( x ) = 2ax + b
(1)
(2)
(3)
K (0) = 20
⇔
d = 20
K (2) = E (2) ⇔ 8a + 4b + 2c + d = 58
⇔ 25a + 5b + c
= 10
kv (5) = 10
(4)
kv ′ (5) = 0
Lösen des LGS ergibt:
⇔ 10a + b
= 0
K ( x ) = x 3 − 10 x 2 + 35 x + 20
7.2.1
5
K
E
Gewinnzone
4
7.2.2 Gewinnzone siehe Zeichnung.
Die Nutzenschwelle gibt die Produktionsmenge an, ab der ein Betrieb einen
Gewinn erwirtschaften kann. Die beträgt hier xNS = 2 .
Die Nutzengrenze markiert diejenige Produktionsmenge, bis zu der ein Betrieb
gewinnbringend arbeitet. Die liegt hier bei xNG = 9,1 .
7.2.3 Gesucht:
Ansatz:
4
kurzfristige Preisuntergrenze kv ( xmin )
bei xmin ist das Minimum der variablen Stückkostenfunktion kv
kv ( x ) = x 2 − 10 x + 35
xmin = 5
damit ist:
und
kv ( xmin ) = 10
4
PRÜFUNG DER FACHHOCHSCHULREIFE
Nachprüfung
an Berufskollegs zum Erwerb der Fachhochschulreife u.a.
2007
Fach : M a t h e m a t i k
Aufgabe 7 (Seite 2/2)
LÖSUNGSVORSCHLAG
7.3.1
Punkte
G( x ) = E ( x ) − K ( x )
= ( −4 x + 40)x − x 3 + 10 x 2 − 35 x − 20
damit sind:
xG max ≈ 4,38
G( xG max ) ≈ 32,98
(gewinnmaximale Produktionsmenge)
(maximaler Gewinn)
3
p( xG max ) ≈ 22,48
C(4,38 | 22,48)
(gewinnmaximaler Preis)
(Cournotscher Punkt)
2
Zeichnet man die Gewinn- und die Preis-Absatz-Kurve in ein gemeinsames
Schaubild, schneidet die Senkrechte durch den Hochpunkt der Gewinnkurve
die Preis-Absatz-Kurve im Cournotschen Punkt.
3
7.3.2 Zeichnung von K und E*:
wobei
E * ( x ) = − 4 x 2 + 31,5 x
K
E*
Im Schaubild ist erkennbar, dass es keine Gewinnzone gibt. Der Betrieb B
kann also nicht verlustfrei arbeiten.
3
_____
30