Aufgaben zur Kostentheorie

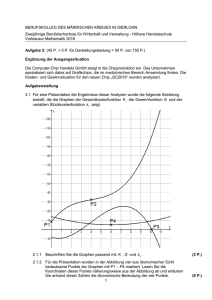
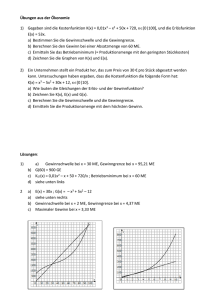
Aufgaben zur Kostentheorie
Aufgabe 1
Die Gesamtkosten K eines Unternehmens hängen von der Produktionsmenge x ab und werden
durch eine ganzrationale Funktion dritten Grades beschrieben. Innerhalb des Unternehmens
sind folgende Informationen bekannt:

Die variablen Kosten ergeben sich durch die Funktionsgleichung:
Kv(x) = x³ - 4x² + 9x

Das Unternehmen befindet sich auf dem Markt in vollständiger Konkurrenz und kann
den Preis nicht selbst festlegen. Der Marktpreis je ME beträgt 85 GE.

Bei einer Produktionsmenge von 2 ME betragen die Gesamtkosten 170 GE.

Die Gewinngrenze des Unternehmens liegt bei 10 ME.

Die Kapazitätsgrenze des Unternehmens liegt bei 11 ME
1.
Stellen Sie die Funktionsgleichungen der Gesamtkosten-, Erlös- und Gewinnfunktion
auf.
2.
Zeigen Sie, dass das Unternehmen bei einer Produktionsmenge von 1 ME einen Verlust
erzielt.
3.
Bestimmen Sie die Gewinn- und Verlustzonen des Unternehmens.
4.
Berechnen Sie die gewinnmaximale Menge und den maximalen Gewinn, den das
Unternehmen erzielen kann.
5.
Nehmen Sie an, dass der Verkaufspreis des Produktes um 5 GE fällt, aber das
Unternehmen gleichzeitig die Fixkosten um 5 GE senken kann. Untersuchen Sie, ob
sich dadurch die Gewinnzone des Unternehmens ändert.
6.
Untersuchen Sie das Steigungsverhalten der Gesamtkostenfunktion. Berechnen Sie
dazu die Steigungen an den Stellen x=0, x=2, x=4, x=6, x=8 und x=10. Beschreiben Sie
anhand der berechneten Werte das Steigungsverhalten verbal.
7.
Berechnen Sie die Steigung der Gewinnfunktion an der Stelle 9. Welche Information
können Sie aus dieser Rechnung über den Verlauf der Gewinnfunktion an dieser Stelle
ziehen?
8.
Skizzieren Sie den Verlauf der Gewinn-, Erlös- und Gesamtkostenfunktion qualitativ
und beschriften Sie die Skizze mit allen ökonomisch relevanten Daten.
Aufgabe 2
Der Produzent eines klinischen Gerätes bietet als einziger auf dem Markt die Ware an.
Dadurch gibt es einen Zusammenhang zwischen Preis und Menge, der über die PreisAbsatz-Funktion p mit der Funktionsgleichung p(x) = -5x + 40 gegeben ist.
Bei der Produktion der Ware ist der Verlauf der Grenzkosten (Steigung der Gesamtkosten)
gegeben durch die Gleichung:
K ( x)  3x 2  16 x  28
Die Fixkosten betragen 10 GE.
1.
Stellen Sie die Gleichung der Gesamtkostenfunktion K auf.
2.
Stellen Sie die Gleichung der Erlös- und Gewinnfunktion auf.
(Kontrollergebnisse: K(x) = x³ - 8x² + 28x +10, E(x) = -5x² + 40x und G(x) = -x³ + 3x²
+ 12x -10)
3.
Berechnen Sie Höchstpreis und Sättigungsmenge für das Produkt.
4.
Bestimmen Sie diejenigen Produktionsmengen, für die der Erlös des Unternehmens
genau 60 GE beträgt.
5.
Zeigen Sie, dass bei einer Produktionsmenge von 5 ME Kosten und Erlöse gleich hoch
sind. Bestimmen anschließend die Gewinnzone des Unternehmens.
6.
Untersuchen Sie, ob der Verlauf der Gewinnfunktion an der Stelle 4 steigend oder
fallend ist. Wenn das Unternehmen die Produktionsmenge ausgehend von 4 ME
steigert, wie verändert sich dann der Gewinn des Unternehmens?
7.
Berechnen Sie den maximalen Gewinn, den das Unternehmen erzielen kann.
8.
Zeichnen Sie den Verlauf der Gesamtkosten-, Erlös- und Gewinnfunktion gemeinsam
in ein Koordinatensystem. Erstellen Sie dazu zunächst eine Wertetabelle und erstellen
Sie das Koordinatensystem in folgenden Bereichen:
x-Achse von 0 bis 6 ME
x
E(x)
K(x)
G(X)
0
1
y-Achse von 0 bis 100 ME
2
3
4
5
6
Beschriften Sie das Koordinatensystem mit folgenden ökonomsch relevanten Daten




Fixkosten
Sättigungsmenge
Gewinnschwelle und Gewinngrenze
erlösmaximale Menge und maximaler Erlös
y
100
90
80
70
60
50
40
30
20
10
x
-1
1
-10
2
3
4
5
6
7
8
Lösungen der Aufgaben zur Vorbereitung auf die Klausur
Aufgabe 1
1.
Fixkosten: Kfix= 160 GE
K(x) = x³ - 4x² + 9x + 160
E(X) = 85x
G(x) = -x³ + 4x² + 76x -160
2.
G(1) = - 81 , also Verlust
3.
Gewinnzone von 2 bis 10 ME
Verlustzonen von 0 bis 2 und von 10 bis 11 ME.
4.
gewinnmaximale Menge: 6,54 ME
maximaler Gewinn: 228 GE
5.
Die Gewinnzone ändert sich. Die Gewinnschwelle liegt nicht mehr bei 2 ME und die
Gewinngrenze nicht mehr bei 10 ME, denn
G(2) = -5 und G(10) = -45
6.
K’(0)= 9
K’(2) = 5
K’(4) = 25
K’(6) = 69
K’(8) = 137
K’(10) = 229
Die Steigungswerte werden zunächst kleiner, steigen jedoch ab x = 4 wieder an.
7.
G’(9) = - 95
Die Gewinnfunktion ist an dieser Stelle fallend.
8.
900
y
800
700
600
500
400
300
200
100
x
-4
-3
-2
-1
1
2
3
4
5
6
7
8
9
10
11
12
13
-100
-200
Aufgabe 2
1.
Zur Bestimmung der Gesamtkostenfunktion muss aus der Ableitung K’(x) die Funktion
K gebildet werden, d.h. die Ableitung muss „rückgängig“ gemacht werden.
Wenn K’ die Funktionsgleichung K’(x) = 3x² - 16x + 28 besitzt, dann muss die
Funktion K wie folgt aussehen:
K(x) = x³ - 8x² + 28x + Fixkosten
Da die Fixkosten lt. Aufgabenstellung 10 GE betragen gilt insgesamt:
K(x) = x³ - 8x² + 28x + 10
2.
vgl. Kontrollergebnisse
3.
Höchstpreis: 40 GE
Sättigungsmenge: 8 ME
4.
E(x) = 60 ergibt die Werte x = 6 (ME) und x = 2 (ME).
5.
G(5) = 0 (bei 5 ME liegt also die Gewinnschwelle oder die Gewinngrenze)
Die Gewinnzone geht von 0,73 ME bis 5 ME
14
6.
G’(4) = -12
Die Gewinnfunktion ist also an der Stelle x = 4 fallend. Würde das Unternehmen die
Produktionsmenge ausgehend von 4 ME steigern, so würde der Gewinn geringer
werden.
7.
Der maximale Gewinn des Unternehmens beträgt 26,36 GE.
y
8.
180
140
100
60
20
x
1
-20
-60
-100
2
3
4
5
6
7
8