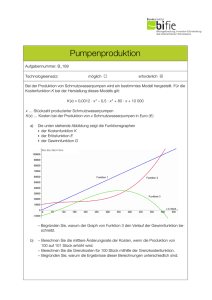
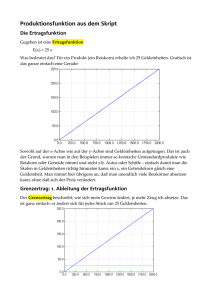
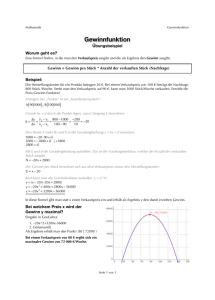
Die Anfrage umfasst Aufgaben zu: Ableiten von Funktionen mit zwei

Die Anfrage umfasst Aufgaben zu:
-
Ableiten von Funktionen mit zwei Variablen
Nullstellenberechnung von Wirtschaftsfunktionen mit einer Variablen
Wendepunktbestimmung und Stellungnahme zum Krümmungsverhalten der Funktion
Die ersten zwei Aufgaben sind nur mit Lösungen. Die dritte Aufgabe beinhaltet Lösungswege. Es sind
keine Angaben darüber zu machen, zu welchem Thema die Aufgaben gehören. Die Themen werden
durcheinander abgefragt. Der Schwierigkeitsgrad der Aufgaben ist mittelschwer.
Aufgabe 1
Folgende Funktionen f in Abhängigkeit der Variablen x und y sind Ihnen gegeben:
𝑦
3
(1) 𝑓(𝑥, 𝑦) = 3 ∗ 𝑥 ∗ 2 − 2𝑥 2 − 𝑦2
1
2
(2) 𝑓(𝑥, 𝑦) = 𝑥 2 −
(3) 𝑓(𝑥, 𝑦) = 𝑎𝑥 2 +
5
3
− √4𝑥𝑦
𝑥𝑦
𝑏
∗ 𝑦 − 𝑐2
6
3
8
(4) 𝑓(𝑥, 𝑦) = 𝑦 ∗ 2𝑥 − √𝑥 6
Bestimmen Sie die ersten Ableitungen nach x sowie y!
Lösungen: zu (1):
𝜕𝑓
𝜕𝑥
𝑦
2
= 3 ∗ − 4𝑥 = 1,5𝑦 − 4𝑥;
3𝑦
𝜕𝑓
− 2𝑦 ∗ (4𝑥𝑦)−0,5; 𝜕𝑦
(𝑥𝑦)2
10
4 𝜕𝑓
+ 𝑥 3 ; 𝜕𝑦 = −10𝑥𝑦 −2
𝑦
=
3𝑥
(𝑥𝑦)2
𝜕𝑓
𝜕𝑦
1
2
𝜕𝑓
𝜕𝑥
6
𝜕𝑓
; zu (2): = 𝑥
𝑦3
𝜕𝑥
𝑏
1
𝜕𝑓
= 6 𝑏; zu (4): 𝜕𝑥 =
6
= 3 ∗ 𝑥 ∗ + 6𝑦 −3 = 1,5𝑥 −
− 2𝑥 ∗ (4𝑥𝑦)−0,5; zu (3):
= 2𝑎𝑥;
𝜕𝑓
)
𝜕𝑦
=
+
Aufgabe 2
Der Gewinn einer Unternehmung sei durch eine Funktion mit der Bezeichnung G definiert und steht
in Abhängigkeit der Menge an Produkten x. Die dazugehörige Funktion lautet
𝐺 = −√8𝑥 6 +
220
− 1600𝑥 − 40.000
𝑥 −2
a. Bestimmen Sie die Wendestelle x der Gewinnfunktion!
b. Nehmen Sie Stellung zum Krümmungsverhalten der Gewinnfunktion! Gehen Sie davon aus,
dass keine negativen Ergebnisse x dem Definitionsbereich zugehörig sind!
Lösung: zu a) x=36,67 (gerundet),; zu b) Die Funktion ist von x=0 bis x=36,67 linksgekrümmt und bis
ins Unendliche rechtsgekrümmt.
Aufgabe 3
Der Preis einer Unternehmung für das Gut x liegt bei konstant 100 Geldeinheiten. Die Kosten K lauten
𝐾(𝑥) = √𝑥 4 + 37,5𝑥 + 625
a. Bestimmen Sie die Gewinnfunktion 𝐺(𝑥) (𝐺(𝑥) = 𝐸(𝑥) − 𝐾(𝑥))!
b. Ermitteln Sie die Mengen an Gütern die notwendig ist, um erstmals einen Gewinn von
weniger als null Geldeinheiten zu erwirtschaften!
Lösung: zu a) Die Aufgabe gibt schon einen Hinweis für die Berechnung. Da der Preis bei 100 liegt,
lautet die Preisfunktion p=100. Die Erlösfunktion (E=Preis*Menge, d.h.𝐸(𝑥) = 𝑝(𝑥) ∗ 𝑥, lautet somit
𝐸(𝑥) = 100 ∗ 𝑥. Folglich kann die Gewinnfunktion wie folgt berechnet werden: 𝐺 = 100𝑥 −
(𝑥 2 + 37,5𝑥 + 625). Dies wird weiter zusammengefasst: 𝐺 = 100𝑥 − 𝑥 2 − 37,5𝑥 − 625
= −𝑥 2 + 62,5𝑥 − 625. Hierbei wurde der erste Ausdruck der Kostenfunktion zuvor wie folgt
4
ungeformt: 𝐾(𝑥) = √𝑥 4 = 𝑥 2 = 𝑥 2 .
Zu b: Es ist nach der Menge x gesucht, wo der Gewinn erstmalig null wird (erste Nullstelle). Also ist die
Gewinnfunktion gleich dem Wert null zu setzen. Dann ist diese aufzulösen. Da die Funktion zweiten
Grades ist (der höchste Exponent ist zwei), kann die Funktion maximal zwei Nullstellen haben. Die
Rechnung geht wie folgt:
𝐺(𝑥) = 0
−𝑥 2 + 62,5𝑥 − 625 = 0
Schon jetzt kann man sehen, dass die pq-Formel anzuwenden ist. Zuvor ist das Minus-Zeichen vor dem
𝑥 2 zu eliminieren. Danach wird die pq-Formel angewandt.
−𝑥 2 + 62,5𝑥 − 625 = 0
| ∗ (−1)
𝑥 2 − 62,5𝑥 + 625
| 𝑝𝑞 − 𝐹𝑜𝑟𝑚𝑒𝑙
𝑥1,2 = −
−62,5
−62,5 2
± √(
) − 625
2
2
𝑥1,2 = 31,25 ± √976,5625 − 625
𝑥1,2 = 31,25 ± √351,5625
𝑥1,2 = 31,25 ± 18,75
𝑥1 = 50
𝑥2 = 12,5
Der kleinere Wert von x=12,5 ist die erste Nullstelle. Folglich wird bei x=12,5 erstmalig ein Gewinn von
null erzielt. Dies nennt man auch Gewinnschwelle.