2. ¨Ubung zur Vorlesung Statistik 2

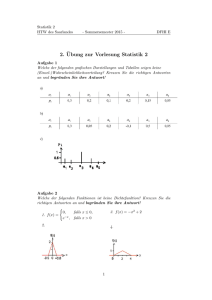
Statistik 2
HTW des Saarlandes
- Sommersemester 2012 -
DFHI E
2. Übung zur Vorlesung Statistik 2
Aufgabe 1
Welche der folgenden grafischen Darstellungen und Tabellen zeigen keine
(Einzel-)Wahrscheinlichkeitsverteilung? Kreuzen Sie die richtigen Antworten
an und begründen Sie ihre Antwort!
Aufgabe 2
Welche der folgenden Funktionen ist keine Dichtefunktion? Kreuzen Sie die
richtigen Antworten an und begründen Sie ihre Antwort!
(
3. f (x ) = −x 2 + 2
0,
falls x ≤ 0,
1. f (x ) =
e −x , falls x > 0
2.
4.
1
Statistik 2
HTW des Saarlandes
- Sommersemester 2012 -
DFHI E
Aufgabe 3
Welche der folgenden Funktionen ist keine Verteilungsfunktion? Kreuzen Sie
die richtigen Antworten an und begründen Sie ihre Antwort!
(
4. F (x ) = 1 − e −|x |
0,
falls x ≤ 0,
1. F (x ) =
(1 + e −x ), falls x > 0
5.
(
0,
falls x < 0,
2. F (x ) =
−x
(1 − e ), falls x ≥ 0
3.
Aufgabe 4
In einem Lieferung von 5 Motorteilen befinden sich 2 defekte Teile.
Zur Qualitätskontrolle werden nacheinander 3 Teile gezogen, ohne sie nach der
Ziehung wieder ins die Lieferung zurück zu legen.
Sei X die Anzahl der unter diesen 3 gezogenenen Teilen vorhandenen defekten
Teile.
1. Berechnen Sie die Wahrscheinlichkeitsverteilung der Zufallsgröße X, d.h.
po = P (X = 0), p1 = P (X = 1) und p2 = P (X = 2).
2. Berechnen Sie den Erwartungswert E (X ), die Varianz Var (X ) und das
untere Quartil x0.25 .
Aufgabe 5
Die zufällige Zeit X, die eine S-Bahn in München verspätet an einer Haltestelle
eintrifft, liegt zwischen 0 und 3 Minuten. Die Dichtefunktion ist in folgender
Skizze gegeben.
Berechnen Sie
1. die Verteilungsfunktion von X.
2
Statistik 2
HTW des Saarlandes
- Sommersemester 2012 -
DFHI E
2. den Anteil der Fällen, in denen die Verspätung eine Minute überschreitet.
Stellen Sie diesen Anteil grafisch dar!
3. die Wahrscheinlichkeit dafür, dass die S-Bahn sich mehr als 2 Minuten
verspätet, wenn man bereits eine Minute (Verspätung) auf die S-Bahn
gewartet hat. Stellen Sie diese Wahrscheinlichkeit grafisch dar.
4. Welche Verspätungszeit wird in 90% aller Fälle überschritten?
5. Wie groß ist die Verspätung im Mittel?
Aufgabe 6
Die Dichtefunktion des zufälligen Lebensdauer X in Jahren eines Bauelementes
hat folgende Gestalt:
Berechnen Sie
1. A und geben Sie f (x ) als Funktionsgleichung an.
2. die Verteilungsfunktion f(x) von X.
3. die erwartete mittlere Lebensdauer.
4. den Anteil der Bauelemente, deren Lebensdauer 11,5 Jahre überschreitet.
Stellen Sie diesen Anteil in der obigen Dichtefunktion grafisch dar.
5. die Lebensdauer, die nur 15% alle Bauelemente überschreiten.
Aufgabe 7
Gegeben ist eine stetige Zufallsvariable mit

2

−3x − 3x
f (x ) = −3x 2 + 3x


0
folgender Dichtefunktion:
, −1 ≤ x ≤ 0
,0 < x ≤ 1
, sonst
1. Berechnen Sie die Verteilungsfunktion.
2. Berechnen Sie den Erwartungswert.
3. Berechnen Sie P (−0, 5 ≤ x ≤ 0, 25).
3
Statistik 2
HTW des Saarlandes
- Sommersemester 2012 -
DFHI E
4. Berechnen Sie P (x ≤ 0, 5|x ≤ 0).
Aufgabe 8
Die Anzahl der eintreffenden Signale an einem Empfänger ist poissonverteilt
mit λ = 2/ms.
1. Wie groß ist die Wahrscheinlichkeit dafür, dass mindestens 3 Signale pro
ms am Empfänger eintreffen?
2. Wie viele Signale treffen im Durchschnitt pro ms beim Empfänger ein?
Aufgabe 9
Die Lebensdauer T von KFZ-Batterien des Typs Bleinix“ ist exponentialver”
teilt mit der erwarteten Lebensdauer E(T) = 3 Jahre.
1. Wieviel % aller Batterien haben eine Lebensdauer > 3 Jahre?
2. Welche Lebensdauer überschreiten 90% aller Batterien nicht?
Aufgabe 10
In der Fabrik eines großen Automobilunternehmens werden an einem Fließband
unter anderem 4 Werkzeugmaschinen W1 , W2 , W3 und W4 eingesetzt. Die
Ausfallwahrscheinlichkeit jeder Werkzeugmaschine pro Tag beträgt 0, 01. Die
Ausfälle an den einzelnen Werkzeugmaschinen sind stochastisch unabhängig.
Berechnen Sie folgende Wahrscheinlichkeiten:
a) genau die Werkzeugmaschine W2 fällt aus.
b) genau einer der Werkzeugmaschinen fällt aus.
c) genau die Werkzeugmaschinen W1 und W4 fallen aus.
d) genau zwei Werkzeugmaschinen fallen aus.
e) höchstens eine Werkzeugmaschine fällt aus.
Aufgabe 11
Bei der Produktion von Rohren schwankt der Normwert des Innendurchmessers
X wie folgt normalverteilt um 100mm: X ∼ N (100, (0, 1)2 ). Alle Rohre, deren Innendurchmesser nicht im Intervall [99, 85; 100, 15] mm liegen, gelten als
Ausschuß!
1. Berechnen Sie die Ausschußrate (Anteil aller Rohre, die Ausschuss sind)
der Produktion!
2. Berechnen Sie den Toleranzbereich um 100 mm herum, d.h. das , so dass
genau 1% aller Rohre außerhalb des Toleranzbereiches [100 − , 100 + ]
liegen!
4
Statistik 2
HTW des Saarlandes
- Sommersemester 2012 -
DFHI E
Aufgabe 12
Die zufällige Übertragungszeit T von Bildsignalen durch einen Kanal K sei normalverteilt mit dem Erwartungswert µ = 50 ms und der Varianz σ 2 = 4ms 2 ,
d.h. es gelte T ∼ N (50, 4).
Signal
K
Empfänger
a) Wie groß ist die Wahrscheinlichkeit dafür, dass die Übertragungszeit genau 42 ms dauert?
b) Mit welcher Wahrscheinlichkeit liegt die Übertragungszeit zwischen 42 und
53 ms?
c) Geben Sie einen symmetrischen Bereich [50−c, 50+c] ms um die mittlere
Übertragungszeit an, in dem 90 % aller Zeiten liegen!
d) Mit welcher Wahrscheinlichkeit beträgt die Übertragungszeit eines Bildsignales mehr als 50ms?
e) Wie groß ist die Wahrscheinlichkeit dafür, dass bei 5 (stochastisch unabhängigen) Übertragungen bei mindestens einer die Übertragungszeit mehr
als 50 ms beträgt?
f ) Wie viele Übertragungen, die länger als 50ms dauern, würden Sie durchschnittlich bei 100 stochastisch unabhängigen Übertragungen erwarten?
g) Angenommen, Sie schalten 2 dieser Kanäle in Reihe. Mit welcher Wahrscheinlichkeit überschreitet die Gesamt-Übertragungszeit dann 100 ms?
Signal
K1
K2
Empfänger
Aufgabe 13
Bei der Herstellung von Wellen sind alle Wellen Ausschuss, die 2mm oder mehr
vom Sollmaß von 150mm Länge abweichen. Die zufällig schwankende Länge hat
den Erwartungswert 150mm, und die Standardabweichung 0,2mm.
Wie groß ist der Aussschussanteil höchstens?
Aufgabe 14
Eine Gerät besteht aus 3 Bauelementen, wie in der Skizze dargestellt. Das Gerät
fällt aus, wenn beide Reihen ausfallen. Eine Reihe fällt aus, wenn mindestens
eines der in Reihe geschalteten Elemente ausfällt.
Die zufällige Zeit Ti bis zum Ausfall eines Bauelements Bi ist wie folgt gegeben
(alle Angaben in Stunden):
• Bauelement B1 : T1 ∼ N (100, 1)
• Bauelement B2 : Die Verteilung von T2 ist nicht vollständig bekannt.
• Bauelement B3 : T3 ∼ E (0, 01)
5
Statistik 2
HTW des Saarlandes
- Sommersemester 2012 -
DFHI E
B1 fällt unabhängig von B3 aus, gleichfalls fällt B2 unabhängig von B3 aus (d.h.
T1 und T2 sind stochastisch unabhängig von T3 ). Die Ausfallwahrscheinlichkeit
von B2 ist von der Lebensdauer von B1 abhängig; es gilt:
P (T2 < 100/T1 < 100) = 0, 99 und P (T2 < 100/T1 ≥ 100) = 0, 2.
Berechnen Sie die Wahrscheinlichkeit dafür, dass die Lebensdauer des Gerätes
100 Stunden nicht überschreitet !
6