Probabilistische Primzahltests Gliederung

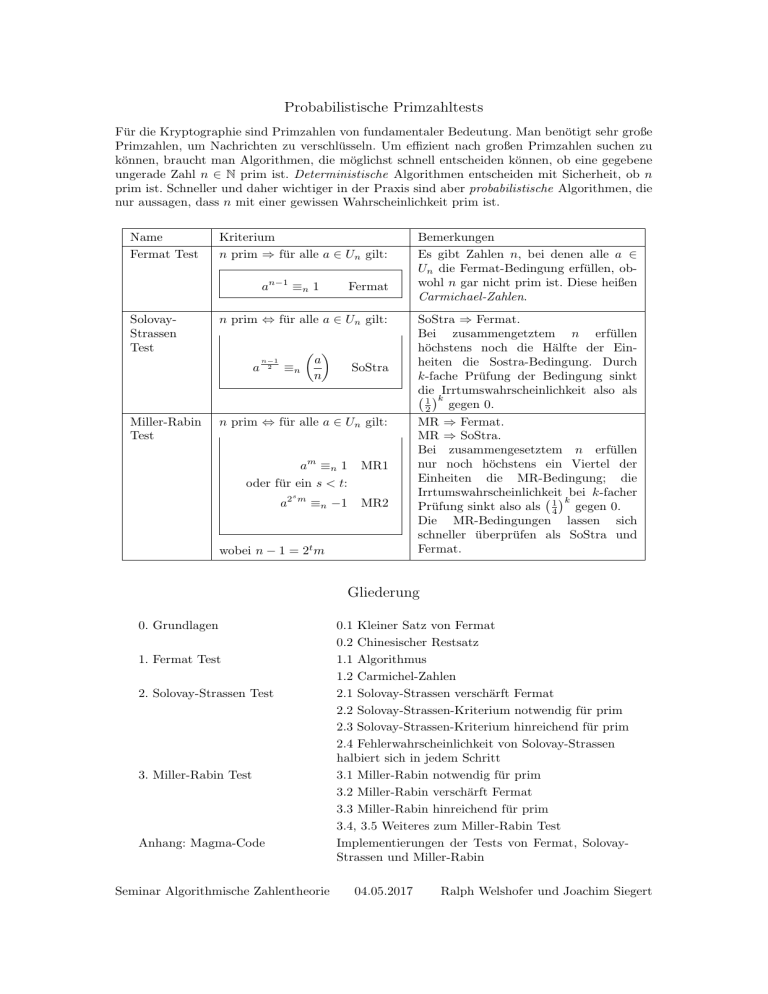
Probabilistische Primzahltests
Für die Kryptographie sind Primzahlen von fundamentaler Bedeutung. Man benötigt sehr große
Primzahlen, um Nachrichten zu verschlüsseln. Um effizient nach großen Primzahlen suchen zu
können, braucht man Algorithmen, die möglichst schnell entscheiden können, ob eine gegebene
ungerade Zahl n ∈ N prim ist. Deterministische Algorithmen entscheiden mit Sicherheit, ob n
prim ist. Schneller und daher wichtiger in der Praxis sind aber probabilistische Algorithmen, die
nur aussagen, dass n mit einer gewissen Wahrscheinlichkeit prim ist.
Name
Fermat Test
Kriterium
n prim ⇒ für alle a ∈ Un gilt:
an−1 ≡n 1
SolovayStrassen
Test
n prim ⇔ für alle a ∈ Un gilt:
a
Miller-Rabin
Test
Fermat
n−1
2
≡n
a
n
SoStra
n prim ⇔ für alle a ∈ Un gilt:
am ≡n 1
MR1
oder für ein s < t:
s
a2
m
≡n −1
MR2
wobei n − 1 = 2t m
Bemerkungen
Es gibt Zahlen n, bei denen alle a ∈
Un die Fermat-Bedingung erfüllen, obwohl n gar nicht prim ist. Diese heißen
Carmichael-Zahlen.
SoStra ⇒ Fermat.
Bei zusammengetztem n erfüllen
höchstens noch die Hälfte der Einheiten die Sostra-Bedingung. Durch
k-fache Prüfung der Bedingung sinkt
die Irrtumswahrscheinlichkeit also als
1 k
gegen 0.
2
MR ⇒ Fermat.
MR ⇒ SoStra.
Bei zusammengesetztem n erfüllen
nur noch höchstens ein Viertel der
Einheiten die MR-Bedingung; die
Irrtumswahrscheinlichkeit bei k-facher
k
Prüfung sinkt also als 41 gegen 0.
Die MR-Bedingungen lassen sich
schneller überprüfen als SoStra und
Fermat.
Gliederung
0. Grundlagen
1. Fermat Test
2. Solovay-Strassen Test
3. Miller-Rabin Test
Anhang: Magma-Code
Seminar Algorithmische Zahlentheorie
0.1 Kleiner Satz von Fermat
0.2 Chinesischer Restsatz
1.1 Algorithmus
1.2 Carmichel-Zahlen
2.1 Solovay-Strassen verschärft Fermat
2.2 Solovay-Strassen-Kriterium notwendig für prim
2.3 Solovay-Strassen-Kriterium hinreichend für prim
2.4 Fehlerwahrscheinlichkeit von Solovay-Strassen
halbiert sich in jedem Schritt
3.1 Miller-Rabin notwendig für prim
3.2 Miller-Rabin verschärft Fermat
3.3 Miller-Rabin hinreichend für prim
3.4, 3.5 Weiteres zum Miller-Rabin Test
Implementierungen der Tests von Fermat, SolovayStrassen und Miller-Rabin
04.05.2017
Ralph Welshofer und Joachim Siegert
0. Grundlagen
Die folgenden Tests beruhen auf dem chinesischen Restsatz und entwickeln den kleinen Satz von
Fermat weiter. Wir formulieren beide für Restklassen. Dabei bezeichne Un die Einheitengruppe
(engl. unit group“ ) modulo n, d. h. Un := (Z/nZ)× . Damit enthält Un genau die Restklassen
”
der Zahlen a, die zu n teilerfremd sind.
Kleiner Satz von Fermat: Sei n ∈ N. Dann gilt: n prim ⇒ an−1 ≡n 1 für alle a ∈ Un .
Beweis: Sei n prim und a ∈ Un . Da n prim ist, hat die Einheitengruppe genau n − 1 Elemente.
In endlichen Gruppen gilt stets: ElementGruppenordnung =Neutralelement. Also an−1 ≡n 1 für alle
a ∈ Un .
Chinesischer Restsatz: Sei n = m1 · . . . · mr ein Produkt teilerfremder Zahlen m1 , . . . mr .
Dann gibt es zu jedem Kongruenzgleichungssystem
x ≡m 1 c 1
x ≡m 2 c 2
...
x ≡m r c r
genau eine Lösung a in Z/nZ. Diese bijektive Zuordnung a ↔ (c1 , . . . , cr ) ist homomorph,
also ein Isomorphismus
Z/nZ ' Z/m1 Z × . . . × Z/mr Z.
Beweis und Algorithmus zur Lösung eines Kongruenzgleichungssystems: Siehe [G §4]. Wir halten
noch eine Folgerung fest:
Z/nZ ' Z/m1 Z × . . . × Z/mr Z
⇒
⇒
⇔
×
Chinesischer Restsatz
×
(Z/nZ) ' (Z/m1 Z × . . . × Z/mr Z)
×
×
(Z/nZ) ' (Z/m1 Z) × . . . × (Z/mr Z)
[G Lemma 4.6(i)]
×
Un ' Um1 × . . . × Umr
[G Lemma 4.6(ii)]
in kürzerer Notation
Insbesondere für die Einheitengruppen können wir den chinesischen Restsatz also einsetzen, und
das werden wir uns in den folgenden Beweisen mehrfach zu Nutze machen.
Seminar Algorithmische Zahlentheorie
04.05.2017
Ralph Welshofer und Joachim Siegert
1. Der Fermat Test
Ist n prim, so erfüllen alle a ∈ Un die Fermat-Bedingung an−1 ≡n 1. Damit können wir eine Zahl
n wie folgt testen:
Wähle zufälliges a ∈ {2, . . . , n − 1}.
Falls an−1 6≡n 1, so n sicher nicht prim.
Falls an−1 ≡n 1, so n vielleicht prim.
Wiederhole ggf. mit neuem a.
Beweis: Angenommen, der Algorithmus stößt auf ein 1 < a < n mit an−1 6≡n 1. Entweder ist a eine Einheit oder nicht. Falls a eine Einheit ist, so haben wir eine Einheit, die die Fermat-Bedingung
verletzt; dann kann n nicht prim sein. Falls a keine Einheit ist, so ist a nicht teilerfremd zu n,
also hat n weitere Teiler neben 1 und sich selbst und kann daher ebenfalls nicht prim sein.
Ein a, das die Bedingung des Primzahltests erfüllt, heißt Zeuge. Ist n aber gar nicht prim und
a trotzdem ein Zeuge, so heißt a spezieller ein falscher Zeuge. Ein a, das die Bedingung verletzt
und daher beweist, dass n nicht prim, nennen wir Gegenzeuge.
Die Aussage, dass n vielleicht prim“ ist, lässt sich beim Fermat Test nicht leicht mit einer Wahr”
scheinlichkeit quantifizieren. Eine Schwierigkeit ist folgende: Es gibt zusammengesetzte Zahlen
n, so dass dennoch alle a ∈ Un die Fermat-Bedingung erfüllen. Solche Zahlen, zu denen alle
Einheiten falsche Fermat-Zeugen sind, heißen Carmichael-Zahlen. Die kleinste Carmichael-Zahl
ist 561 = 3 · 11 · 17. Die folgenden Tests sollen besser mit ihnen zurechtkommen als der Fermat
Test. Dafür werden sie folgende Eigenschaft solcher Zahlen ausnutzen:
Lemma: Carmichael-Zahlen sind quadratfrei. Ist n ∈ N eine ungerade zusammengesetzte Zahl, so dass alle a ∈ Un die Fermat-Bedingung an−1 ≡n 1 erfüllen, dann lautet die
Primfaktorzerlegung n = p11 · . . . · p1r , d. h. kein Primfaktor tritt in einer Potenz größer als 1
auf (n ist Produkt paarweise verschiedener Primzahlen).
Beweis: Sei n eine ungerade zusammengesetzte Zahl mit an−1 ≡n 1 für alle a ∈ Un . Angenommen,
es gäbe eine Primpotenz pe (e > 1), die n teilt. Dann können wir n schreiben als n = pe m mit
m (Produkt der übrigen Primfaktoren) teilerfremd zu pe . Gemäß chinesischem Restsatz gilt
Un ' Upe × Um .
Sei ζ eine Primitivwurzel modulo pe , d. h. ein Erzeuger von Upe . Der chinesische Restsatz liefert
ein a ∈ Un mit der simultanen Kongruenz
a ≡p e ζ
a ≡m 1
(diese Wahl ist beliebig)
Nach Annahme gilt ferner an−1 ≡n 1. Da pe ein Teiler von n ist, gilt also erst recht an−1 ≡pe 1.
Mit obiger Kongruenz folgt ζ n−1 ≡pe an−1 ≡pe 1. Also muss ord (ζ) ein Teiler von n − 1 sein.
Wir erhalten
ord (ζ) = ϕ(pe ) = pe−1 (p − 1) | n − 1
⇒
pe−1 | n − 1
e>1
⇒
p | n − 1,
unmöglich, da p | n. Also kann es keine Primpotenz geben, die n teilt, d. h. n muss quadratfrei
sein.
Seminar Algorithmische Zahlentheorie
04.05.2017
Ralph Welshofer und Joachim Siegert
2. Der Solovay-Strassen Test
Der Solovay-Strassen Test entwickelt den Fermat Test weiter, indem er eine Bedingung testet,
die nicht nur notwendig, sondern auch hinreichend für Primzahlen ist. Wenn also für gegebenes
n alle a ∈ Un die Solovay-Strassen Bedingung erfüllen, so muss n prim sein. Wir können sogar
abschätzen: Ist n zusammengesetzt, so sind höchstens die Hälfte der a ∈ Un falsche Zeugen.
Dieser Test lässt sich daher probabilistisch nutzen: Mit jedem gefundenen Zeugen halbiert sich
die Wahrscheinlichkeit, dass n nicht prim ist.
Solovay-Strassen-Kriterium: Sei n ∈ N ungerade. Dann gilt:
n−1
a
für alle a ∈ Un
n prim ⇔ a 2 ≡n
n
wobei rechts das Jacobi-Symbol steht. Ist n nicht prim, so erfüllen höchstens noch die Hälfte
der a ∈ Un diese Gleichung.
Beweis:
(1) Solovay-Strassen verschärft Fermat Bedingung
Sei n ∈ N eine ungerade Zahl und a ∈ Un ein Element, das die Solovay-Strassen Bedingung erfüllt.
Da n ungerade ist und a teilerfremd zu n, nimmt das Jacobi-Symbol einen der Werte ±1 an. Es
gilt also:
n−1
2
a
⇒
n−1
a
≡n ±1
nach Annahme
≡n 1
durch Quadrieren
Jedes a, das die Solovay-Strassen-Bedingung erfüllt, erfüllt also erst recht die Fermat-Bedingung.
(2) Ist n prim, so erfüllen alle a ∈ Un die Solovay-Strassen Bedingung
a
n−1
2
Sei n ∈ N ungerade und eine Primzahl. Dann gilt a
≡n
für alle a ∈ Un gemäß dem
n
Lemma von Euler (vgl. Referat vom 27.4.).
(3) Ist n nicht prim, so verletzt ein a ∈ Un die Solovay-Strassen Bedingung
Sei n ∈ N eine ungerade zusammengesetzte Zahl. Angenommen, alle a ∈ Un würden die SolovayStrassen Bedingung erfüllen. Gemäß (1) erfüllen sie dann alle erst recht die Fermat Bedingung.
Somit ist n eine Carmichael-Zahl. Mit obigem Lemma ist also n = p1 ·. . . pr ein Produkt paarweise
verschiedener Primzahlen. Gemäß chinesischem Restsatz gilt die Isomorphie
Un ' Up1 × . . . × Upr
Wieder sei ζ eine Primitvwurzel modulo p1 . Der chinesische Restsatz garantiert nun ein eindeutiges a in Un , das folgende Kongruenzen erfüllt:
a ≡p1 ζ
a ≡p2 1
...
a ≡pr 1
Seminar Algorithmische Zahlentheorie
04.05.2017
Ralph Welshofer und Joachim Siegert
Damit gilt für das Jacobi-Symbol:
a
a
=
n
p1 · · · pr
a
a
a
=
...
p1
p2
pr
ζ
1
1
=
···
p1
p2
pr
= −1 · 1
···
Multiplikativität des Jacobi-Symbols
a
b
mit der Regel a ≡m b ⇒
=
m
m
1
siehe unten
= −1
denn 1 = 12 ist ein Quadrat modulo jeder Zahl, und eine Primitivwurzel modulo Primzahl (außer
2) ist niemals ein Quadrat: Wäre nämlich ζ ≡p1 b2 für ein b ∈ Up1 , so wäre, da hζi = Up1 die
ganze Gruppe erzeugt, zugleich b ≡p1 ζ k für ein k ∈ N, also ζ ≡p1 ζ 2k und daher 1 ≡p1 ζ 2k−1 ,
also ord (ζ) ein Teiler von 2k − 1, insbesondere ungerade. Aber ord (ζ) = p1 − 1 gerade (da p1
Primzahl größer als 2), unmöglich. Daher gilt
ζ
= −1.
p1
Nach Widerspruchsannahme erfüllen alle Einheiten die Solovay-Strassen-Bedingung, insbesondere das von uns konstruierte a:
n−1
a
2
≡n
a
≡n −1.
n
n−1
n−1
Wegen a 2 ≡n −1 gilt erst recht a 2 ≡p2 −1. Aber das ist unmöglich, denn a ist so konstrun−1
iert, dass a ≡p2 1, also auch a 2 ≡p2 1, und da p2 eine Primzahl größer als 2 ist, gilt 1 6≡p2 −1.
Bei einer zusammengesetzten Zahl n muss es also mindestens einen Gegenzeugen zur SolovayStrassen Bedingung geben.
(4) Ist n nicht prim, so sind höchstens die Hälfte der a ∈ Un falsche Zeugen
Sei n eine zusammengesetzte Zahl. Dann ist die Menge der falschen Solovay-Strassen-Zeugen
n−1
a
2
F = a ∈ Un | a
≡n
n
eine Untergruppe von Un , wie wir mit dem Untergruppenkriterium sehen: Seinen a, b ∈ F falsche
Zeugen. Dann gilt für ab−1 :
(ab−1 )
n−1
2
n−1
n−1
≡n a 2 (b 2 )−1
−1
a
b
≡n
n n
−1 a
b
≡n
n
n
−1 ab
≡n
n
denn
denn a, b ∈ F
b−1
b
bb−1
1
=
=
=1
n
n
n
n
Multiplikativität des Jacobi-Symbols
und damit ist auch ab−1 ∈ F , also F eine Untergruppe von Un . F muss sogar eine echte Untergruppe sein, denn in (3) haben wir gesehen, dass nicht ganz Un aus falschen Zeugen bestehen
kann. Als echte Untergruppe der endlichen Gruppe Un ist F höchstens halb so groß wie Un .
Für die Praxis bedeutet dies: Mit jedem zufälligen a ∈ Un , das die Solovay-Strassen-Bedingung
erfüllt, halbiert sich die Wahrscheinlichkeit, dass n keine Primzahl ist. Durch k-faches Testen
k
konvergiert die Fehlerwahrscheinlichkeit dieses Primzahltests als 21 rasch gegen null.
Seminar Algorithmische Zahlentheorie
04.05.2017
Ralph Welshofer und Joachim Siegert
3. Der Miller-Rabin Test
Der Miller-Rabin Test ist eine noch mächtigere Weiterentwicklung des Fermat Tests und erfreut
sich in der Praxis großer Beliebtheit. Um ihn zu verstehen, überlegen wir uns zuerst an einem
Beispiel, wie man schnell potenzieren kann. Wir wollen untersuchen, ob n = 2017 eine Primzahl ist. Dazu wählen wir zufälliges a aus U2017 . Für den Fermat Test müssten wir nun a2016
berechnen. Die definitorisch naheliegende Herangehensweise a2016 = a · a · a · . . . · a erfordert 2015
Multiplikationen. Das geht besser: Wir zerlegen n−1 = 2016 = 4·504 = 16·126 = 32·63 = 25 ·63
in seinen geraden und seinen ungeraden Anteil und Potenzieren nun durch
a2016 = a63·32 = (a63 )32
= (((((a63 )2 )2 )2 )2 )2
Notieren wir n − 1 = m · 2t , wobei m der ungerade Anteil ist (hier: m = 63 und t = 5), so lautet
t
t
dies allgemein: an−1 = am2 = (am )2 . Die ungerade Potenz a63 lässt sich übrigens ihrerseits mit
Hilfe schrittweisen Quadrierens effizient berechnen:
a63 = a32+16+8+4+2+1 = a32 a16 a8 a4 a2 a
= ((((a2 )2 )2 )2 )2 (((a2 )2 )2 )2 ((a2 )2 )2 (a2 )2 a2 a
Nun von rechts unten aus startend: Wir rechnen a mal (a mal a), merken uns letzeren Zwischenwert, rechnen erneut mal a, und so fortfahrend benötigen wir insgesamt nur elf (!) Multiplikationen, bis wir bei a2016 angekommen sind. Unterwegs, im zehnten Schritt, erhalten wir als
n−1
Zwischenergebnis a 2 , denjenigen Wert, den wir für den Solovay-Strassen Test bräuchten.
s
(1) Ist n prim, so ist am ≡n 1 oder es gibt ein s < t mit (am )2 ≡n −1
Sei n eine Primzahl. Laut kleinem Satz von Fermat ist dann an−1 ≡n 1. Wir zerlegen n−1 = m·2t
t−1
t−1
in geraden und ungeraden Anteil. Für die nächstkleinere Stufe (am )2
gilt ((am )2 )2 =
t
(am )2 = an−1 ≡n 1; sie ist eine Quadratwurzel der Eins.
t−1
Es muss also (am )2
≡n ±1 sein: n ist prim, also Z/nZ ein Körper, und über einem Körper
hat die Gleichung x2 = 1 ⇔ x2 − 1 = 0 ⇔ (x − 1)(x + 1) = 0 nur ±1 als Lösungen. ∗
s
t
(am )2 ≡n 1
t−1
(am )2
(am )2
≡n 1
t−1
≡n −1
...
1
(am )2 ≡n 1
0
(am )2 ≡n 1
0
(am )2 ≡n −1
Ist ein (am )2 ≡n 1, so folgt
s−1
wiederum (am )2
≡n ±1, und
es ergibt sich nebenstehender
Baum. Jeder Zweig entspricht
dabei einer Quadratur bzw. Radizierung.
t
Damit sich letztlich (am )2 ≡n 1
ergeben kann, muss also am ≡n
1 gelten (unteres linkes Blatt)
s
oder (am )2 ≡n −1 für ein s ∈
{0, . . . , t − 1} (rechte Blätter),
wie behauptet.
s
(2) Ist am ≡n 1 oder es gibt ein s < t mit (am )2 ≡n −1, so folgt an−1 ≡n 1
Starten wir in einem der Blätter des obigen Baumes, so ergibt sich durch (mindestens einfaches)
Quadrieren sogleich 1 als Wert und dieser ändert sich unter weiterem Quadrieren nicht mehr.
∗ Gegenbeispiel für n nicht prim: In Z/8Z ist 12 ≡ 1 und 32 ≡ 9 ≡ 1 und 52 ≡ 25 ≡ 1 und 72 ≡ 49 ≡ 1,
8
8
8
8
8
8
8
womit die Gleichung x2 ≡8 1 vier Lösungen besitzt. Dass Polynome zweiten Grades höchstens zwei Nullstellen
haben, ist nur über Körpern wahr.
Seminar Algorithmische Zahlentheorie
04.05.2017
Ralph Welshofer und Joachim Siegert
Miller-Rabin-Kriterium: Sei n ∈ N ungerade, und n − 1 = 2t m (mit m ungerade) die
Zerlegung von n − 1 in Zweierpotenz und übrigen Faktor. Es gilt:
n prim ⇔ alle a ∈ Un erfüllen mindestens eine der Bedingungen
am ≡n 1
2s m
a
(MR1)
≡n −1 für ein s ∈ {0, . . . , t − 1}
(MR2)
Beweis:
In (1) haben wir gezeigt: n prim ⇒ alle a ∈ Un erfüllen MR1 oder MR2. In (2) haben wir
gezeigt, dass jedes a ∈ Un , das MR1 oder MR2 erfüllt, erst recht die Fermat-Bedingung erfüllt.
Bleibt zu zeigen:
(3) Ist n nicht prim, so verletzt ein a ∈ Un die Miller-Rabin-Bedingung
Sei n ∈ N eine ungerade zusammengesetzte Zahl. Angenommen, alle a ∈ Un würden eine der
Bedingungen MR1 und MR2 erfüllen. Da alle a die Miller-Rabin-Bedingung erfüllen, erfüllen sie
laut (2) auch die Fermat-Bedingung. Somit ist n eine Carmichael-Zahl. Wieder nutzen wir, dass
n = p1 · . . . · pr quadratfrei,ist. Da n zusammengesetzt und quadratfrei ist, gibt es also mindestens
zwei Primfaktoren p1 und p2 . Da wir von vornherein ungerades n betrachten, sind diese beiden
Primfaktoren beide ungleich 2. Wieder setzen wir den chinesischen Restsatz ein:
Un ' Up1 × . . . × Upr
und wählen ein a ∈ Un wie folgt: Sei ζ erneut eine Primitivwurzel modulo p1 . Sei nun a dasjenige
Element von Un mit
a ≡p 1 ζ
a ≡p 2 1
Nach Annahme erfüllt a eine der Bedingungen MR1 und MR2. Falls a MR1 erfüllt, so gilt
am ≡n 1. Also erst recht am ≡p1 1. Wegen a ≡p1 ζ folgt ζ m ≡p1 am ≡p1 1. Also ist ord (ζ) ein
Teiler von m:
ord (ζ) = p1 − 1 | m,
unmöglich, da p1 − 1 gerade, m jedoch ungerade ist.
Falls a die andere Bedingung MR2 erfüllt, so a2
s
erst recht a2 m ≡p2 −1, und mit a ≡p2 1 folgt:
s
12
m
s
m
≡n −1 für ein s ∈ {0, . . . , t − 1}. Also
≡p2 −1,
unmöglich, da 1 unter Potenzieren immer 1 bleibt, und 1 ≡p −1 nur für p = 2 gilt; in allen
anderen Restklassenringen sind 1 und −1 verschieden. Es kann also nicht sein, dass bei einer
zusammengesetzten Zahl n alle a ∈ Un die Miller-Rabin-Bedingung erfüllen.
Der Miller-Rabin Test verwendet also, wie auch Solovay-Strassen, eine genau dann, wenn“”
Bedingung für Primzahlen. Er lässt sich aber deutlich schneller ausführen: Erstens genügen ihm
n−1
oft schon kleinere Potenzen als a 2 , die für die Prüfung gemäß Fermat oder Solovay-Strassen
ohnehin als Zwischenwerte nötig wären, und zweitens braucht er diese Potenzen nur mit ±1 zu
vergleichen anstatt noch ein Jacobi-Symbol berechnen zu müssen.
Seminar Algorithmische Zahlentheorie
04.05.2017
Ralph Welshofer und Joachim Siegert
Der Miller-Rabin Test ist nicht nur schneller als der Solovay-Strassen Test, sondern auch
gründlicher:
(4) Miller-Rabin verschärft Solovay-Strassen
Ohne Beweis. Siehe dazu [K 131ff]. Da jedes a ∈ Un , das die Miller-Rabin-Bedingung erfüllt, erst
recht die Solovay-Strassen-Bedingung erfüllt, ist der Miller-Rabin Test mindestens so gründlich
wie der Solovay-Strassen Test; seine Fehlerwahrscheinlichkeit muss sich in jedem Schritt also
mindestens halbieren. Tatsächlich gilt sogar:
(5) Ist n nicht prim, so sind höchstens ein Viertel der a ∈ Un falsche Zeugen
Ohne Beweis. Siehe dazu [MSP 92f]. Die Tests von Solovay-Strassen und Miller-Rabin sind also
schrittweise Weiterentwicklungen des kleinen Satzes von Fermat, die es ermöglichen, effizient zu
testen, ob eine gegebene Zahl prim ist. Die Wahrscheinlichkeit, dass eine zusammengesetzte Zahl
diese Tests besteht, kann so schnell so weit gesenkt werden, dass sie vernachlässigbar wird beispielsweise gegenüber der Wahrscheinlichkeit eines Hardware-Fehlers. Somit sind probabilistische
Primzahltests für viele kryptographische Anwendungen das Mittel der Wahl.
Literatur
[G]
[K]
Gerkmann, R.: Zahlentheorie, Vorlesungsskript aus dem WS2016/17.
Koblitz, N.: A course in number theory and cryptrography, Graduate Texts in
Mathematics 114, 2. Auflage, Springer 1994.
[MSP] Müller-Stach, S./Piontkowski, J.: Elementare und algebraische Zahlentheorie,
2. Auflage, Vieweg+Teubner 2011.
Seminar Algorithmische Zahlentheorie
04.05.2017
Ralph Welshofer und Joachim Siegert
Anhang: Magma-Code
1
2
3
// Fermat Test
n:=561;
R:=ResidueClassRing(n);
4
5
6
7
8
9
10
11
12
13
14
for i:=1 to 10 do
a:=Random(R);
print "a=",a;
if (not (a^(n-1) eq 1)) then
print "a^(n-1)=",a^(n-1), "also", n, "keine Primzahl";
break;
else
print a, "^(",n-1,")=",a^(n-1)," erfuellt die Fermat-Bedingung";
end if;
end for;
Testet die Zahl n (hier 561) höchstens zehn mal (Zeile 5/14), indem für ein zufälliges Element
von Z/nZ (Zeile 6) die Fermat-Bedingung überprüft wird. Ist diese verletzt, so bricht der Test
mit der Meldung ab, dass n keine Primzahl ist (Zeile 9, 10).
1
2
3
// Solovay-Strassen Test
n:=41041;
R:=ResidueClassRing(n);
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
for k:=1 to 10 do
a:=Random(1,n);
if (not (GCD(a,n) eq 1)) then
print a,"nicht teilerfremd zu",n,"also n sicher nicht prim";
break;
else
if (not ((R!a)^((n-1) div 2) eq JacobiSymbol(a,n))) then
print a,"^(n-1)/2=",(R!a)^((n-1) div 2),"aber Jacobi-Symbol=",
JacobiSymbol(a,n), "also",n, "sicher nicht prim";
break;
else
print a,"^(n-1)/2=",(R!a)^((n-1) div 2),"und Jacobi-Symbol=",
JacobiSymbol(a,n), "also",n, "max. mit Wkeit",(1/2)^k,"nicht prim";
end if;
end if;
end for;
Gegenüber dem Fermat Test kommt die if-Schaltung in Zeilen 7/10 hinzu: Wir prüfen erst, ob
das gezogene a < n teilerfremd zu n ist. Wenn nein, dann ist n sicher nicht prim; Ende des Tests
(Zeile 9). Wenn ja, dann ist a eine Einheit, und wir prüfen, ob die Solovay-Strassen-Bedingung
erfüllt ist. Erfüllt die Einheit sie (Zeile 15ff), dann sinkt die Wahrscheinlichkeit, dass n nicht
k
prim ist, auf 21 . Diese Prüfung auf Teilerfremdheit (Zeile 7) kostet zwar Rechenzeit, die wir
uns im Fermat Test sparen konnten, aber nur dank der Gewissheit, eine Einheit zu untersuchen,
erhalten wir dann die in 2.3 und 2.4 bewiesene Fehlerabschätzung.
Etwas Sorgfalt ist übrigens bei der Wahl der Typen geboten: Zeile 6 muss a ∈ Z als ganze Zahl
generieren, weil die Funktion JacobiSymbol (Zeile 11) nur ganze Zahlen akzeptiert. An allen
anderen Stellen wollen wir stattdessen die Restklasse [a]n ∈ Z/nZ betrachten, was wir jeweils
durch den typecast R!a erzwingen (interpretiert a als Element von R = Z/nZ).
Seminar Algorithmische Zahlentheorie
04.05.2017
Ralph Welshofer und Joachim Siegert
1
2
3
// Miller-Rabin Test
n:= 3825123056546413051;
R:=ResidueClassRing(n);
4
5
6
7
8
// Vorbereitungen für Miller-Rabin
f:=Factorization(n-1);
t:=f[1][2]; // besorgt die 2er Potenz, die in n-1=2^t*m enthalten ist
m:=(n-1) div (2^t); // besorgt den übrigen ungeraden Faktor m
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
// teste höchstens 10 mal
for k:=1 to 10 do
a:=Random(R);
// teste, ob a Einheit
if (not (GCD(a,n) eq 1)) then
print a,"nicht teilerfremd zu",n,"also n sicher nicht prim";
else
// Teste, ob MR1 erfüllt
x:=a^m;
if (x eq 1) then
print a,"^m=1, also n hoechstens mit Wkeit",(1/4)^k,"nicht prim";
// Falls MR1 nicht erfüllt, teste, ob MR2 erfüllt
else
treffer:=false;
s:=0;
while ((not treffer) and (s lt t)) do
if (x eq -1) then
treffer:=true;
print a,"^(m*2^",s,")=-1, also n hoechstens mit Wkeit",
(1/4)^k,"nicht prim";
break;
else
s:=s+1;
x:=x^2;
end if;
end while;
if (s eq t) then
print a,"erfuellt die MR-Bedingung nicht,
also n sicher keine Primzahl";
break;
end if;
end if;
end if;
end for;
Ergänzend zu den Kommentaren im Code: In Zeile 18 wird am als eigene Variable x angelegt,
n−1
damit wir dann schrittweise quadrieren können bis a 2 (das geschieht jeweils in Zeile 33).
Solution([1,1,1],[2,1,1],[3,11,17]);
Lösung eines Kongruenzgleichungssystems:
Seminar Algorithmische Zahlentheorie
04.05.2017
1·x≡2
mod 3
1·x≡1
mod 11
1·x≡1
mod 17
Ralph Welshofer und Joachim Siegert