Ubungsblatt 4 MAT121.1 Analysis 1

Übungsblatt 4
MAT121.1 Analysis 1
Herbstsemester 2016
Prof. Dr. Camillo De Lellis
Die Übungsblätter werden jeweils am Freitag auf der Homepage der Vorlesung publiziert.
Für den Leistungsnachweis müssen mindestens 8 gelöste Übungsblätter mit mindestens 12 Punkten abgegeben
und insgesamt mindestens 280 Punkte erreicht werden. Generell soll die Herleitung der Resultate übersichtlich
sein, und es wird gebeten, leserlich zu schreiben.
Abgabe : 21. Oktober 13:00 im Briefkasten “Analysis 1 Mat 121.1” im K-Stock am Institut für Mathematik
Aufgabe 1 (12 Punkte)
Schreiben Sie die folgenden komplexen Zahlen in der Form a + ib mit a, b ∈ R:
(i) z1 =
(ii) z2 =
(iii) z3 =
(iv) z4 =
(v) z5 =
3+2i
2−i .
(1+2i)3
|3−3i| .
1+2i
1−i
+ (1 + 3i).
(4−i)(4+i)
.
2−i
1−i
1+i .
(vi) z6 = ( 1i +
1 2
i3 ) .
Zeichnen Sie die folgenden Teilmengen der komplexen Zahlenebene:
1. A1 = {z ∈ C : |z − i| ≥ Im(z)}.
2. A2 = {z ∈ C : Re(z) > Im(z)}.
Lösung:
(i)
z1 =
3 + 2i
(3 + 2i)(2 + i)
6 + 3i + 4i − 2
4 + 7i
4 7
=
=
=
= + i.
2−i
4+1
5
5
5 5
(ii)
z2 =
1 + 6i − 12 − 8i
11
2
(1 + 2i)3
√
=
= − √ − √ i.
|3 − 3i|
18
3 2 3 2
(iii)
z3 =
1 + 2i
1−i
+ (1 + 3i) =
(1 + 2i)(1 + i)
1+1
1
+ (1 + 3i) =
1 + i + 2i − 2 + 2 + 6i
1 9
= + i.
2
2 2
(iv)
z4 =
(4 − i)(4 + i)
(4 − i)2
(15 − 8i)(2 + i)
30 + 15i − 16i + 8
38 1
=
=
=
=
− i.
2−i
2−i
4+1
5
5
5
(v)
z5 =
1−i
(1 − i)2
1 − 1 − 2i
=
=
= −i.
1+i
1+1
1+1
(vi)
1
1
z6 = ( + 3 )2 = (−i + i)2 = 0.
i
i
1. Wir identifizieren C mit R2 , wobei einer Zahl z = x + iy ∈ C der Punkt (x, y) ∈ R2 zugeordnet
wird (und umgekehrt). Mit dieser Identifikation ist
|z − i| ≥ Im(z) ⇐⇒
p
x2 + (y − 1)2 ≥ y.
Diese Ungleichung ist für alle (x, y) ∈ R × (−∞, 0] (die Wurzel kann nicht kleiner als Null sein)
erfüllt. Falls y ≥ 0, dann
p
x2
1
x2 + (y − 1)2 ≥ y ⇐⇒ x2 + y 2 + 1 − 2y ≥ y 2 ⇐⇒ y ≤
+ .
2
2
Somit ist die Lösungsmenge {(x, y) ∈ R2 : y ≤
x2
2
+ 12 } ⊃ R × (−∞, 0].
Im(z)
x2
2
+
1
2
Re(z)
2. Wir identifizieren C mit R2 , wobei einer Zahl z = x + iy ∈ C der Punkt (x, y) ∈ R2 zugeordnet
wird (und umgekehrt). Mit dieser Identifikation ist
Re(z) > Im(z) ⇐⇒ x > −y ⇐⇒ y > −x.
Somit ist die Lösungsmenge {(x, y) ∈ R2 : y > −x}.
2
Im(z)
3i
2i
y
-3
-2
1i
=
−
x
-1
Re(z)
0i
0
1
2
3
-1i
-2i
-3i
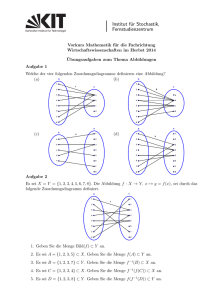
Aufgabe 2 (12 Punkte)
Beweisen Sie, ob die folgenden Funktionen injektiv, surjektiv oder bijektiv sind:
(i) f1 : x ∈ [0, 1) 7→ x ∈ [0, 1].
(ii) f2 : x ∈ R 7→ x2 ∈ R+ := {x ∈ R : x ≥ 0}.
(iii) f3 : x ∈ R 7→ x4 ∈ R.
(iv) f4 : x ∈ N 7→ x + 3 ∈ N ∩ [3, ∞).
(v) f5 : x ∈ R \ {0} 7→
1
x
∈ R.
x
(vi) f6 : x ∈ R 7→ e + 1 ∈ R+ := {x ∈ R : x ≥ 0}.
(vii) f7 : (x, y) ∈ R2 7→ (x, y, 0) ∈ R3 .
(viii) f8 : (x, y) ∈ R2 7→ x + y ∈ R.
Lösung:
(i) Falls f1 (x) = f1 (y), dann x = y. Demnach f1 ist injektiv. Da f1 (x) 6= 1 für jedes x ∈ [0, 1), ist f2
nicht surjektiv. Demnach ist f1 nicht bijektiv.
(ii) f2 (−1) = 1 = f2 (1), also ist f2 nicht injektiv. Demnach ist f2 nicht bijektiv. Für jedes a ∈ R+
√
haben wir f2 ( a) = a. Wir folgern, dass f2 surjektiv ist.
(iii) f3 (−1) = 1 = f3 (1), also ist f3 nicht injektiv. Demnach ist f3 nicht bijektiv. Für jedes a < 0
existiert kein x ∈ R, sodass f3 (x) = a. Wir folgern, dass f3 nicht surjektiv ist.
(iv) Falls n+3 = f4 (n) = f4 (m) = m+3, dann n = m. Demnach ist f4 injektiv. Für jedes n ∈ N∩[3, ∞),
haben wir n − 3 ∈ N und f4 (n − 3) = n. Demnach ist f4 surjektiv und bijektiv.
(v) Für jedes (x, y) ∈ (R \ {0})2 folgt aus x1 = f5 (x) = f5 (y) = y1 , dass x = y. Demnach ist f5 injektiv.
Für jedes x ∈ R \ {0} haben wir f5 (x) 6= 0 ∈ R. Demnach ist f4 nicht surjektiv und nicht bijektiv.
(vi) Für jedes (x, y) ∈ R2 folgt aus ex + 1 = f6 (x) = f6 (y) = ey + 1, dass x = y. Demnach ist f6
injektiv. Da ex + 1 > 1 für jedes x ∈ R, existiert für jedes a ∈ [0, 1] kein x ∈ R, sodass f6 (x) = a.
Demnach ist f6 nicht surjektiv und nicht bijektiv.
(vii) Für jedes ((x, y), (v, w)) ∈ (R2 )2 folgt aus (x, y, 0) = f7 ((x, y)) = f6 ((v, w)) = (v, w, 0), dass
(x, y) = (v, w). Demnach ist f7 injektiv. Für jedes (x, y, z) ∈ R3 mit z 6= 0 haben wir (x, y, z) 6∈
f7 (R2 ). Demnach ist f6 nicht surjektiv und nicht bijektiv.
3
(viii) f8 ((x, y)) = f8 ((y, x)) für jedes (x, y) ∈ R2 . Demanch f8 ist nicht injektiv und nicht bijektiv. Für
jedes x ∈ R haben wir f8 ((x, 0)) = x. Wir folgern, dass f8 surjektiv ist.
Aufgabe 3 (12 Punkte)
Sei Φ : Q → R, sodass
(i) Φ(1) = a > 0,
(ii) Φ(q + r) = Φ(q) · Φ(r) für jedes (q, r) ∈ Q2 .
Zeigen Sie, dass Φ(q) = aq für jedes q ∈ Q.
Lösung:
Wir bemerken, dass
a = Φ(1) = Φ(1 + 0) = Φ(1) · Φ(0) = a · Φ(0).
Da a 6= 0, dann
Φ(0) = 1 = a0 .
(1)
Demnach für jedes q ∈ Q haben wir 1 = Φ(0) = Φ(q − q) = Φ(q)Φ(−q) und
Φ(−q) =
1
.
Φ(q)
(2)
Für jedes n ∈ N \ {0} behaupten wir, dass
Φ
n
X
!
qi
=
i=1
n
Y
∀(q1 , . . . , qn ) ∈ Qn .
Φ(qi ),
(3)
i=1
Wir können die Behauptung beispielsweise per Induktion zeigen.
Induktionsanfang: Für n = 1 gilt Φ(q1 ) = Φ(q1 ).
Induktionsschritt: Nehme an, wir hätten die Ungleichung bereits für ein n ∈ N, n ≥ 1 bewiesen. Wir
rechnen
Φ
n+1
X
!
qi
=Φ
i=1
n
X
i=1
!
qi + qn+1
=Φ
n
X
!
qi
· Φ(qn+1 ) =
i=1
n
Y
!
Φ(qi )
· Φ(qn+1 ) =
i=1
n+1
Y
Φ(qi ).
i=1
Also gilt die Ungleichung offenbar auch für n + 1.
Induktionsschluss: Für jedes n ∈ N \ {0} gilt die Behauptung (3).
Mit Hilfe von (3), für jedes n ∈ N \ {0} rechnen wir
n
X
1
a = Φ(1) = Φ
n
i=1
!
n
Y
n
1
1
=
Φ
= Φ
.
n
n
i=1
Wir folgern, dass
√
1
Φ
= n a.
n
(4)
Für jedes q ∈ Q ∩ (0, ∞) existiert (m, n) ∈ N2 , n, m 6= 0, sodass q = m
n . Mit Hilfe von (3) und (4),
rechnen wir
!
m
m
m
m
X
Y
m
1
1
1
Φ(q) = Φ
=Φ
=
Φ
= Φ
= a n = aq .
(5)
n
n
n
n
i=1
i=1
4
Mit Hilfe von (2), für jedes q ∈ Q ∩ (−∞, 0), rechnen wir
Φ(q) =
1
1
= −q = aq .
Φ(−q)
a
(6)
Von (1), (5) und (6) folgern wir, dass Φ(q) = aq für jedes q ∈ Q, wie gewünscht.
Φ(q)
aq
Bemerkung: Wenn wir Ψ : q ∈ Q →
(i) Ψ(1) =
Φ(1)
a
(ii) Ψ(q + r) =
betrachten, dann
= 1,
Φ(q+r)
aq+r
=
Φ(q)·Φ(r)
aq ·ar
=
Φ(q)
aq
·
Φ(r)
ar
= Ψ(q) · Ψ(r) für jedes (q, r) ∈ Q2 .
Demnach, wäre es ausreichend gewesen, die Aufgabe für den Fall a = 1 zu lösen.
Aufgabe 4 (12 Punkte)
Seien f : X → Y eine Funktion, A, B zwei Teilmengen von X und C, D zwei Teilmengen von Y . Beweisen
Sie die folgenden Sätze:
(i) f (A ∪ B) = f (A) ∪ f (B).
(ii) f (A ∩ B) ⊆ f (A) ∩ f (B).
(iii) f (A \ B) ⊇ f (A) \ f (B).
(iv) f −1 (C ∪ D) = f −1 (C) ∪ f −1 (D).
(v) f −1 (C ∩ D) = f −1 (C) ∩ f −1 (D).
(vi) f −1 (C \ D) = f −1 (C) \ f −1 (D).
Lösung:
(i)
y ∈ f (A ∪ B) ⇐⇒ ∃x ∈ A ∪ B : f (x) = y ⇐⇒ (∃x ∈ A : f (x) = y) oder (∃z ∈ B : f (z) = y)
⇐⇒ y ∈ f (A) ∪ f (B).
Demnach f (A ∪ B) = f (A) ∪ f (B).
(ii)
y ∈ f (A ∩ B) ⇐⇒ ∃x ∈ A ∩ B : f (x) = y ⇒ (∃x ∈ A : f (x) = y) und (∃z ∈ B : f (z) = y)
⇒ y ∈ f (A) ∩ f (B).
Demnach f (A ∩ B) ⊆ f (A) ∩ f (B).
(iii)
y ∈ f (A) \ f (B) ⇐⇒ (∃x ∈ A : f (x) = y) und (@z ∈ B : f (z) = y) ⇒ ∃x ∈ A \ B : f (x) = y
⇒ y ∈ f (A \ B).
Demnach f (A \ B) ⊇ f (A) \ f (B).
(iv)
x ∈ f −1 (C ∪ D) ⇐⇒ ∃y ∈ C ∪ D : f (x) = y ⇐⇒ (∃y ∈ C : f (x) = y) oder (∃z ∈ D : f (x) = z)
⇐⇒ x ∈ f −1 (C) ∪ f −1 (D).
5
Demnach f −1 (C ∪ D) = f −1 (C) ∪ f −1 (D).
(v)
x ∈ f −1 (C ∩ D) ⇐⇒ ∃y ∈ C ∩ D : f (x) = y ⇐⇒ x ∈ f −1 (C) ∩ f −1 (D).
Demnach f −1 (C ∩ D) = f −1 (C) ∩ f −1 (D).
(vi)
x ∈ f −1 (C \ D) ⇐⇒ ∃y ∈ C \ D : f (x) = y ⇐⇒ x ∈ f −1 (C) \ f −1 (D).
Demnach f −1 (C \ D) = f −1 (C) \ f −1 (D).
Aufgabe 5 (12 Punkte)
Finden Sie ein Polynom f in zwei Variablen mit Koeffizienten, die natürliche Zahlen sind, sodass f beschränkt auf (N \ {0}) × (N \ {0}) injektiv ist.
Bemerkung: ein Polynom f in zwei Variablen mit Koeffizienten, die natürliche Zahlen sind, ist eine Funktion
f : C2 → C von der Gestalt
X
f (x, y) =
aij xi y j ,
i+j≤n
(i,j)∈N2
wobei die Koeffizienten aij für jedes (i, j) ∈ {0, . . . , n}2 natürliche Zahlen sind.
Lösung:
Betrachten Sie
f (x, y) := (x + y)2 + y.
Nehmen Sie an dass (x, y) ∈ (N \ {0}) × (N \ {0}), (v, z) ∈ (N \ {0}) × (N \ {0}) und
(x + y)2 + y = (v + z)2 + z.
Wir behaupten, dass (x, y) = (v, z). Wir führen den Beweis via Widerspruch. Falls (x, y) 6= (v, z), dann
y 6= z, anderenfalls, da x, y, v ∈ N \ {0}
(x + y)2 + y = (v + z)2 + z ⇐⇒ (x + y)2 + y = (v + y)2 + y ⇐⇒ (x + y)2 = (v + y)2 ⇐⇒ x = v.
Das gibt den Widerspruch (x, y) = (v, z).
Demnach entweder k ∈ N \ {0} existiert, sodass z = y + k, oder h ∈ N \ {0} existiert, sodass y = z + h.
Falls k ∈ N \ {0} existiert, sodass z = y + k, dann
(x + y)2 + y = (v + z)2 + z ⇐⇒ (x + y)2 + y = (v + y + k)2 + y + k ⇐⇒ (x + y)2 − (v + y + k)2 = k.
Da x, v, y, k ∈ N \ {0}, folgern wir, dass x + y > v + y + k und x + y ≥ v + y + k + 1. Demnach
k = (x + y)2 − (v + y + k)2 ≥ ((v + y + k) + 1)2 − (v + y + k)2 = 1 + 2(v + y + k),
das ein Widerspruch ist, da v, y ∈ N \ {0}. Der Fall y = z + h gibt einen Widerspruch auf die gleiche
Art und Weise. Demnach gilt (x, y) = (v, z) und f beschränkt auf (N \ {0}) × (N \ {0}) ist injektiv.
6