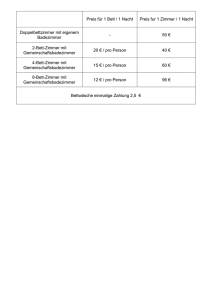
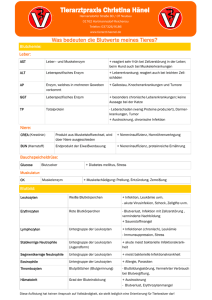
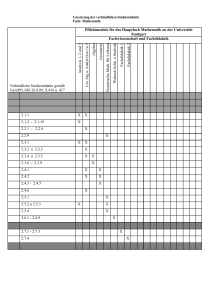
Rolf Walter und

Rolf Walter
Lineare Algebra
und
analytische Geometrie
Aus dem Programm
Mathematik
-----------...
Lineare Algebra und analytische Geometrie I und II
von E. Brieskorn
Lineare Algebra
von G. Fischer
Analytische Geometrie
von G. Fischer
EinfUhrung in die lineare Algebra
von R. Walter
Lineare Algebra und analytische Geometrie
von R. Walter
Projektive Geometrie
von A. Beutelspacher und U. Rosenbaum
Algebra
von E. Kunz
Elementare Zahlentheorie
von G. Frey
Analysis 1, 2 und 3
von O. Forster
Numerische Mathematik fUr Anfiinger
von G. Opfer
Numerische Mathematik 1 und 2
von J. Werner
Funktionentheorie
von W. Fischer und I. Lieb
DiHerentialgeometrie von Kurven und Flachen
von M. P. do Carma
Topologie
von E. Ossa
EinfUhrung in die Funktionalanalysis
von R. Meise und D. Vogt
J
Vieweg _______________~
Rolf Walter
L
Lineare Algebra
und
analytische Geometrie
Zweitel durchgesehene Aufloge
Mit 56 Bildern
II
Vl8weg
Prof. Dr. Rolf Walter
Mathematik VII - Differentialgeometrie
Universitat Dortmund
Vogelpothsweg 87
D-44221 Dortmund
1. Auflage 1985
2., durchgesehene Auflage 1993
Aile Rechte vorbehalten
© Friedr. Vieweg & Sohn Verlagsgesellschaft mbH, Braunschweig/Wicsbaden, 1993
Der Verlag Vieweg ist ein Unternehmen der Verlagsgruppe Bertelsmann International.
Das Werk einschlieBlich aller seiner Teile ist urheberrechtlich geschtitzt. Jede
Verwertung auBerhalb der engen Grenzen des Urheberrechtsgesetzes ist ohne
Zustimmung des Verlags unzulassig und strafbar. Das gilt insbesondere flir
Vervielfaltigungen, Ubersetzungen, Mikroverfilmungen und die Einspeicherung und Verarbeitung in elektronischen System en.
Umschlaggestaltung: Klaus Birk, Wiesbaden
Satz: Vieweg, Braunschweig
Gedruckt auf saurefreiem Papier
ISBN 978-3-528-18584-8
ISBN 978-3-322-91538-2 (eBook)
DOI 10.1007/978-3-322-91538-2
v
Vorwort
Dieses Buch behandelt die lineare und multilineare Algebra sowie die analytische Geometrie. Es ist entstanden aus entsprechenden Vorlesungen des ersten Studienjahres, die ich
mehrfach an den Universitaten Freiburg und Dortmund fUr Mathematiker, Physiker und
Studenten mit mathematischem Nebenfach gehalten habe.
Der Schwerpunkt dieses Buches liegt auf den weiterfi\hrenden Themen des zweiten
Semesters. Jedoch ist die Darstellung weitgehend in sich abgeschlossen, da elementare
Kenntnisse oftmals wiederholt und neu begrtindet werden. Ftir die erstmalige Aneignung
der Grundlagen sei auf meine "Einftihrung in die line are Algebra" (Vieweg) hingewiesen.
Nach algebraischen Vorbereitungen befaBt sich der erste Teil dieses Buches mit allgemeinen
Vektorraumen, Normalformen linearer Abbildungen, komplexen Vektordiumen und
multilinearer Algebra. Hervorzuheben sind die Diskussion der Codimension, der Brtickenschlag zur Analysis in Gestalt der normierten Vektorraume und die Fundierung der Hauptachsentransformation mit dem Rayleighschen Extremalprinzip. Bei den komplexen
Vektorraumen erfolgt ein elementarer Beweis des "Fundamentalsatzes der Algebra", der
im folgenden zutreffender als algebraischer Fundamentalsatz in C bezeichnet wird.
Weiter wird die reelle 10rdansche Normalform rnittels des "Durchganges durch Komplexe'gewonnen. 1m tibrigen sind die komplexen Strukturen so aufgebaut, wie es ein nahtloser
AnschluB an die komplexe Analysis auf Mannigfaltigkeiten erfordert.
Der zweite Teil entwickelt die analytische Geometrie auf der Basis der linearen Algebra,
und zwar getrennt nach den affinen, euklidischen und projektiven Gesichtspunkten,
jeweils mit den spezifischen Hilfsmitteln der betreffenden Struktur. Nach den linearen
Gebilden werden die quadratischen Hyperfhchen behandelt. Der allgemeinen Grundhaltung entsprechend, wird auch in der Geometrie die moderne, basisfreie Denkweise
bevorzugt. Dementsprechend sind die Resultate in einem starkeren AusmaB als sonst
tiblich unabhangig von der endlichen Dimension (und tibrigens auch yom Skalarenkorper).
Wo es geboten erscheint, wird aber der basisfreie Aufbau durch Koordinatenrechnungen
erganzt.
BewuBt bietet dieser Band an einigen Stellen mehr, als in einem Semester erarbeitet werden kann. So konnen die Abschnitte tiber den algebraischen Fundamentalsatz in C und
tiber lordansche Normalform, multilineare Algebra und projektive Geometrie als Wahlmoglichkeiten betrachtet werden. Denn diese Themen werden in anderen Abschnitten
nicht verwendet. Auch sonst wurde auf gegensei tige Unabhangigkei t geachtet. Eine
Sonderrolle spielt das Kapitel 0 tiber Algebra, von dem in der Folge nur einige Grundbegriffe gebraucht werden, das aber fUr die mathematische Allgemeinbildung sehr ntitzlich
ist.
VI
Vorwort
Dem Buch sind zahlreiche Dbungsaufgaben mit vielen Li:isungshinweisen beigegeben.
Die Aufgaben enthalten zum einen konkrete Rechenbeispiele zum Text. Zum anderen
werden durch sie weiterflihrende Themen erschlossen, die sich auch gut fiir ein Proseminar eignen. Dem Leser sei die Beschaftigung mit Ubungsaufgaben besonders empfohlen, urn seine Kraft zu trainieren. (Wer sich z. B. anhand der Bemerkung 2 in 7.5 das
Transformationsverhalten des Doppelverhaltnisses erarbeitet, profitiert fill sich mehr, als
wenn er eine Tabelle mit 23 Eintragen zur Kenntnis nehmen miil1te!) - 1m Text werden
die Aufgaben prinzipiell nicht verwendet.
Insgesamt war mein Ziel ein weitgehend unabhangiges Lehrbuch der linearen Algebra
und analytischen Geometrie, das sowohl der Festigung des Bekannten wie auch dem
Aufbau neuer, relevanter Bezirke dient und das nicht zuletzt als Referenz-Werk fUr
hi:ihere Vorlesungen geeignet ist.
Danken mi:ichte ich auch an dieser Stelle Frau G. Schmidt, geb. Wienke fill ihren unermiidlichen Einsatz bei der Textherstellung, den Herren Dipl.-Math. S. Peters und Dr. W.
Striibing fill Hilfe und wertvolle Ratschlage bei der Korrektur sowie Frau Dr. P. DanzerKatzarova fill ihre Unterstiitzung bei den Bildern. Mein Dank gilt aber auch dem Verlag,
vor allem Frau Schmickler-Hirzebruch, fUr die gute Betreuung des Werkes.
Dortmund, im Juni 1993
Rolf Walter
VII
Zum Gebrauch des Buches
Die acht Kapitel sind in Abschnitte mit jeweils zweistelligen Nummern gegliedert. In
jedem Abschnitt Hingt die Numerierung von Definitionen, Formeln usw. neu an, wobei
Satze und Definitionen gemeinsam mit gro~en lateinischen Buchstaben durchgezahlt
sind. Lediglich die Numerierung der Bilder und Tabellen ist im ganzen Buch durchlaufend.
Verweise erfolgen im gleichen Abschnitt ohne dessen Nennung, an anderen Stellen unter
AnfUgung des zitierten Abschnitts in eckigen Klammern; z.B. verweist "Satz E [5.1]" auf
Satz E des Abschnittes 5.1. Bei einem "Zusatz" werden stets die Voraussetzungen beibehalten. Das Ende einer Uberlegung wird durch das Zeichen D angedeutet, die Zeichen
:= und =: signalisieren eine Definitionsgleichung, wobei der Doppelpunkt auf der Seite
der neu eingefUhrten Gro~e steht. Generalvoraussetzungen, die zu Beginn eines Abschnittes gemacht werden, gelten auch fUr die zugehorigen Aufgaben.
Die Standardmengen der Mathematik sind
N
Z
Q
R
C
Menge
Menge
Menge
Menge
Menge
folgenderma~en
bezeichnet:
der natUrlichen ZaWen (ohne 0)
der ganzen Zahlen
der rationalen Zahlen
der reellen Zahlen
der komplexen Zahlen.
Das Anhangen des Indexes ,,0" bedeutet hier Hinzunahme, die Schreibart ,,\0" Wegnahme
der Null; z.B. ist No die Menge der natUrlichen Zahlen zusammen mit 0, Z\O die Menge Z
ohne 0. Die Marken" +" und ,,-" bezeichnen entsprechende Vorzeicheneinschrankungen;
z.B. ist R+ die Menge aller positiven, R~ die Menge aller nichtnegativen reellen Zahlen.
Am Ende des Buches finden sich Verzeichnisse der Literatur und der weiteren Symbole
sowie das Sachverzeichnis. Hinweise auf das Literaturverzeichnis erfolgen durch Nennung
der Autoren in Kursivschrift (gegebenenfalls mit einer Ordnungsnummer). Das Buch:
"R. Walter, EinfUhrung in die lineare Algebra" wird kurz durch ,,1" zitiert. Das Sachverzeichnis enthalt auch die Lebensdaten der erwahnten Wissenschaftler.
VIII
Inhaltsverzeichnis
o Aus der Algebra
0.1
0.2
0.3
0.4
......................................... .
Gruppen und Untergruppen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. 1
Homomorphe Abbildungen und Faktorgruppen . . . . . . . . . . . . . . . . . . .. 9
Restklassen ganzer Zahlen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16
Ringe und Knrper . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. 21
1 Vektorraume ............................................ 26
1.1
1.2
1.3
1.4
1.5
Grundlagen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ..
Cartesische Produkte und Summen . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Dualitat . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Quotientenraume und Codimension . . . . . . . . . . . . . . . . . . . . . . . . . . ..
Normierte Vektorraume . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ..
26
31
37
47
58
2 Feinstruktur spezieller Endomorphismen euklidischer Vektorraume .. 69
2.1
2.2
2.3
2.4
Hilfsmittel. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ..
Symmetrische Endomorphismen . . . . . . . . . . . . . . . . . . . . . . . . . . . . ..
Isometrische Endomorphismen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Normale Endomorphismen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ..
69
75
81
85
3 Komplexe Vektorraume . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. 89
3.1 Komplexe und reelle Struktur . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 89
3.2 Der algebraische Fundamentalsatz in C . . . . . . . . . . . . . . . . . . . . . . . . . . 101
3.3 Anwendung auf die lordansche Normalform . . . . . . . . . . . . . . . . . . . . . . 103
4 Multilineare Algebra . ...................................... 114
4.1
4.2
4.3
4.4
4.5
4.6
Multilineare Abbildungen und Multilinearformen . . . . . . . . . . . . . . . . . . . 114
Tensorprodukt endlich dimensionaler Vektorraume . . . . . . . . . . . . . . . . . 117
Tensoralgebra tiber einem endlich dimensionalen Vektorraum . . . . . . . . . . . 124
Alternierende multilineare Abbildungen und Formen . . . . . . . . . . . . . . . . 129
AuBere Algebra tiber einem endlich dimensionalen Vektorraum .......... 137
Darstellung von Untervektorraumen und Determinanten in der auBeren
Alge bra . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 148
I nhaltsverzeichn is
IX
5 Affine und euklidische Geometrie ............................ 152
5.1 Affine Geometrie . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .... 153
5.2 Affine Abbildungen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 166
5.3 Euklidische Geometrie . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 173
6 Quadratische Hyperfliichen in der affinen und euklidischen Geometrie . . 177
6.1
6.2
6.3
6.4
Definition und Darstellung von Quadriken . . . . . . . . . . . . . . . . . . . . . . . . 177
Schnitt mit Geraden . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 184
Affine Quadriktypen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 192
Euklidische Quadriktypen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 201
7 Projektive Geometrie ...................................... 211
7.1
7.2
7.3
7.4
7.5
7.6
7.7
7.8
Motivierung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ...... 211
Prazise Definitionen und grundlegende Begriffe . . . . . . . . . . . . . . . . . . . . 212
Das Dualitatsprinzip . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 216
Homogene Koordinaten und projektive Bezugssysteme . . . . . . . . . . . . . . . 219
Das DoppelverhaItnis . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 221
Projektive Abbildungen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 226
Quadriken in der Projektivgeometrie . . . . . . . . . . . . . . . . . . . . . . . . . . . 231
Zusammenhang mit der Affingeometrie . . . . . . . . . . . . . . . . . . . . . . . . . 237
Literaturhinweise ........................................... 248
Wichtige Symbole ........................................... 249
Sachverzeichnis ............................................ 258
o Aus der Algebra
-
Die Algebra, die friiher einmal die Kunst der Gleichungsauflosung war, ist heute in eine
allgemeine Theorie der Verkntipfungen eingemtindet, die zumeist abstrakt, also axiomatisch
betrieben wird. Die axiomatische Denkweise beruht auf der folgenden Grundidee: Man
stellt zunachst fest, da£ gewisse Gesetzma£igkeiten fUr unterschiedliche Objekte gleicherma£en gelten. Daraufhin lost man sich von den konkreten Gi.iltigkeitsbereichen, indem
man solche Gesetze zu defmierenden Eigenschaften einer neuen Struktur erhebt. Dieses
Vorgehen hat sich in der modernen Mathematik au£erordentlich bewiihrt. Einer seiner
Vorztige ist die geistige Okonomie, die es bewirkt: Erkenntnisse, die im abstrakten Rahmen
gewonnen wurden, besitzen eine universelle Gi.iltigkeit; sie brauchen in konkreten Fallen
nicht erneut tiberprtift zu werden. Unter den vielen algebraischen Strukturen, die so aufgebaut wurden, konzentrieren wir uns in diesem Kapitel auf die Gruppen und Korper.
0.1 Gruppen und Untergruppen
Seit der Erfmdung der Gruppenstruktur im 19. Jahrhundert hat dieser Begriff eine starke,
vereinheitlichende Kraft ausgetibt, so da£ er heute zum fundamentalen Rtistzeug des
mathematischen Denkens gehort. Wir stellen den Gruppenbegriff aber nicht nur wegen
seiner gro£en Bedeutung an den Anfang, sondern auch deshalb, well man an ihm den
axiomatischen Zugang zur Algebra in Reinkultur studieren kann. 1m Gegensatz zu den
Zahlenmengen, die man aus der Schule kennt, besitzt eine Gruppe nur eine einzige Verkntipfung, und die Rechenregeln, denen diese folgt, sind denkbar einfach. Umso erstaunlicher ist es, da£ bereits ein kurzer Einstieg handfeste, nichttriviale Erkenntnisse liefert,
z.B. den "kleinen Fermat" und den Satz von Wilson aus der Zahlentheorie, die wir gegen
Ende dieses Kapitels vorstellen.
Grundlagen
Eine Gruppe ist zunachst ein Verkniipfungsgebilde, d.h. eine nichtleere Menge G von Elementen, derart da£ nach einem bestimmten Gesetz je zweien dieser Elemente, a und b,
ein neues Element ab derselben Menge G zugeordnet ist (Abgeschlossenheit). Das Verkntipfungsergebnis von a und b, das hier einfach mit ab bezeichnet wurde, kann auch
anders geschrieben werden, z.B. als a· b (multiplikative Schreibweise) oder als a + b
(additive Schreibweise), und je nachdem wird das Verkntipfungsergebnis auch als Produkt
oder Summe bezeichnet. Will man die Verkntipfung genau speziflzieren, so schreibt man
das Verkntipfungsgebilde als Paar, also etwa (G,·) oder (G, +). 1m allgemeinen verwenden
wir die Schreibweisen ab = a· b simultan. Auf die Reihenfolge der "Faktoren" kommt es
dabei sehr wohl an, d.h. ab ist nicht unbedingt gleich ba. 1st die zugrundeliegende Menge
o Aus der Algebra
2
G endlich, so wird die Anzahl der Elemente durch IG I bezeichnet und die Ordnung von
G genannt.
Damit ein Verkniipfungsgebilde (G, .) eine Gruppe ist, miissen folgende Forderungen erftillt sein:
(G.1) Fur je drei Elemente a, b, c E G gilt das Assoziativgesetz: (ab) c = a(bc).
(G.2) Es gibt ein Neutralelement e E G, d. h. ein Element von G mit der Eigenschaft:
ae = ea = a flir aile a E G.
(G.3) Zu jedem Element a EG existiert ein inverses Element a-I EG, d.h. ein Element
von G, das die Gleichungen aa -I = a-I a = e erflillt.
Aus den ersten beiden Axiomen folgt bereits, d~ das Neutralelement eindeutig bestimmt
ist, so da~ e bei der Formulierung des dritten Axioms schon festliegt. 1m allgemeinen
wird ab =1= ba sein. Gilt jedoch zusatzlich das Axiom:
(G.4) Fur aile a, bEG besteht das Kommutativgesetz ab = ba,
so
hei~t
die Gruppe G kommutativ oder abelsch.
Einfache Folgerungen aus den Gruppenaxiomen (G.l) bis (G.3) sind folgende Tatsachen:
Ebenso wie es nur ein Neutralelement geben kann, ist auch zu jedem Element a E G das
Inverse a-I eindeutig bestimmt. Allgemeiner besitzt jede der Gleichungen ax = b bzw.
ya=b fUr gegebene a,bEG genau eine Lasung in G,niimlichx=a-Ibbzw.y=ba- I .
Ferner hat man (a-Ir l = a fUr alle a E G. Das Assoziativgesetz aus (G.l) iibertragt sich
durch vollstandige Induktion auf n ~ 3 Elemente, so d~ das mehrfache Verknupfungsergebnis al ... an unabhangig von der zunachst natigen Beklammerung ist, diese also weggelassen werden kann. Fiir die Inversenbildung gilt hierbei:
(1)
(al ... ani\-1 -_ (\-1
ani ... ()-I
al
(Reihenfolge!).
Aus demmehrfachen Verkniipfungsergebnis al ... an erhiilt man spezieil fUr al = ... = an =: a
die Potenz an, die durch aO := e und an := (a-n)-I auch fUr nichtpositive ganze Zahlen n
als Exponenten erkHirt ist.
Bei konunutativen Gruppen verwendet man haufig die additive Schreibweise, wobei das
Neutralelement durch 0 (Null), das Inverse von a durch - a (minus a) und die Potenz als
Vielfaches n· a = na bezeichnet werden. Mehrfache Summen werden haufig mit dem
La
n
Summenzeichen geschrieben (Z.B. al + ... + an als
i)
bzw. bei multiplikativer Schreib-
i =1
weise mit demProduktzeichen (z.B. al ... an als
fr
ai )'
i = 1
Wichtige Beispiele erhalt man in Gestalt der Transformationsgruppen, wovon wir den
folgenden Hauptfall hervorheben: 1st eine nichtleere Menge M gegeben, so sei 13 M die
Menge ailer bijektiven Selbstabbildungen a: M 4 M, zusammen mit der Komposition 0 als
Verkniipfung. (13 M , 0) ist dann eine Gruppe, wobei das Neutralelement die identische Abbildung L von M und das Inverse zu a die Umkehrabbildung a-I ist. Jedes a E 13 M heillt
eine Permutation von 11, und 13 M wird deswegen als die (volle) Permutationsgruppe von
0.1 Gruppen und Untergruppen
3
M bezeichnet. Wenn M mindestens drei versehiedene Elemente a, b, e enthalt, so ist eM
nicht kommutativ. Dies sieht man leieht anhand der beiden bijektiven Selbstabbildungen
a, r von M, die auf der dreielementigen Teilmenge {a, b, e} durch
(2)
a(a) := e, a(b):= a, a(c):= b
(3)
r(a) := a, r(b):= c, r(e):= b
und auf M \ {a, b, c} dureh a(x) := rex) := x erkHirt sind. Es gilt dann a o r(a) = c, aber
r 0 a( a) = b, also a 0 r =1= r 0 a. 1m Spezialfall, dafl M die Menge der ersten n natiirliehen
Zahlen -1, ... , n ist, wird eM identisch mit der symmetrischen Gruppe en'
Beispiele fUr kommutative Gruppen liefem die Standardzahlmengen Z, Q, R, mit der gewohnlichen Addition oder die Mengen Q \ 0 und R \ 0 mit der gewohnliehen Multiplikation als Verkntipfung.
1st Heine Teilmenge der (multiplikativ geschriebenen) Gruppe G, so ist fUr je zwei Elemente a, b aus H das Produkt ab definiert. Man wird Heine Untergruppe von G nennen,
wenn hierdurch eine Verkntipfung auf H definiert wird, die den Gruppenaxiomen genilgt.
Notwendig und hinreichend dafUr ist, dafl H folgende Forderungen erfUllt:
(UG.1) e EH;
(UG.2) wenn a E H und b E H, so ab E H;
(UG.3) wenn aEH, so a-I EH.
Fiir nichtleeres H ist (UG.1) eine leiehte Konsequenz aus (UG.2) und (UG.3)_
Jede Gruppe besitzt die beiden trivialen Untergruppen {e} und G, wobei statt {e} haufig
e gesehrieben wird. Aile anderen Untergruppen von G heilien echt.
Faflt man Z, Q, R als additive Gruppen auf, so gilt Z C Q C R, und jede dieser Mengen
ist Untergruppe der folgenden. Weniger triviale Beispiele werden in Ktirze auftreten. Die
line are Algebra liefert ebenfalls einen grof,en Schatz von Gruppen und Untergruppen, die
irn allgemeinen nieht kommutativ sind.
Weiterfiihrung
Das Umgehen mit Teilmengen einer Gruppe (G,') wird dureh folgende Symbolik erleichtert: Sind H, K niehtleere Teilmengen yon G, so sei· HK = H· K die Menge aller Produkte ab, wobei aEH und b EK, und ebenso sei H- I die Menge aller Inversen a-I mit
a E H. 1m Spezialfall, dafl etwa H einelementig ist, H = {e}, sehreibt man haufig etwas
laseh H = c und versteht demgemaf, unter eK die Menge aller Produkte eb mit b E K.
Analog ist Ke := {be Ib E K}. Aus dem Assoziativgesetz fUr Elemente von G folgt unmittelbar das Assoziativgesetz fill dieses ,,Mengenprodukt", narnlich
(4)
(HK)L = H(KL),
so dafl aueh hier auf die Klammem verziehtet werden kann, und aus der Regel ( a-I) -I = a
ergibt sich:
(5)
(Wlr l = H.
o
4
Aus der Algebra
Da man friiher Teilmengen einer Gruppe als "Komplexe" bezeichnet hat, nennt man die
hiermit eingeftihrte Symbolik die Komplexschreibweise. Insbesondere heilit HK das
Komplexprodukt von H und K.
Niitzlich beim Umgehen hiermit sind die folgenden Monotonieregeln:
(6)
die man unmittelbar anhand der Defmition einsieht.
In der Komplexschreibweise lauten die Untergruppenaxiome (UG.l) - (UG.3) so:
(UG.l) e E H
(UG.2) HHsH
(UG.3) WI
s H.
Tatsachlich erkennt man aIs Konsequenz hieraus mittels (5) und (6) die Gleichungen
(7)
HH
= H,
WI
=H,
die also fill jede Untergruppe H ~ G gelten.
Eine geHiufige Art, Untergruppen zu erzeugen, besteht in der sukzessiven Verkniipfung
und Inversenbildung gegebener Elemente. Wir beschreiben dies fUr den einfachsten Fall,
daf, ein einziges festes Element a E G vorgegeben ist: Die genannten sukzessiven Operationen ftihren hier auf die Gesamtheit der Potenzen a r mit beliebigen ganzzahligen Exponenten r. Diese Potenzen erftillen die folgenden Regeln
(8)
aO=e,
aras=a r + s,
(a~s=ars,
(arrl=a- r ,
die man direkt durch Abzahlen der Faktoren und Beachtung der Defmition a- r := (arrl
fUr r > 0 bestatigt. Wenn es nun eine Untergruppe von G gibt, die das Element a enthalt,
so mu~ diese Untergruppe nach (UG.l) - (UG.3) die Menge aller dieser Potenzen en thalten. Wir bezeichnen die Menge dieser Potenzen in Zukunft so:
(9)
[a]:= {... , a- 2 , a-I, e, a, a 2 ,
... }.
Andererseits liest man aus (8) sofort ab, daf, die Menge [a] selbst die Untergruppenaxiome
erftillt, mit anderen Worten: Zu jedem a E Gist [a] die kleinste Untergruppe von G, die a
enthalt. Man nennt [a] monogene Untergruppe von G (mit der Erzeugenden a). Eine soIche
monogene Untergruppe ist stets kommutativ, wie man direkt aus (8) entnimmt. Weiter
kann man die folgenden Falle (ex) und (M unterscheiden:
(ex) Aus r i= s folgt stets ar i= as, d.h. aile Potenzen von a sind paarweise verschieden. In
diesem Fall heilit [a] auch unendliche monogene Untergruppe.
Es gibt r, s mit r < s und ar = as. Dann gilt as - r = e, also existiert hier eine Potenz von
a mit positivem Exponenten, die gleich e ist. Sei q das Minimum aIler positiven ganzen
Zahlen j mit ai = e; q heillt die (endliche) Ordnung des Elementes a. Die Menge der Potenzen ist hier endlich, niimlich:
(~)
(10)
[a]= {e,a,a 2 ,
... ,a q - 1 },
5
0.1 Gruppen und Untergruppen
wobei alle aufgesehriebenen Elemente paarweise versehieden sind (sonst ware q nieht
minimal) und wobei aq = e ist. Zum Beweis der Inklusion ~ von (10) wird die Division
mit Rest in Z benotigt, die wir im folgenden Hilfssatz A fonnulieren. Es folgt damit fUr
jedes rEZ: ar = asq+t = (aq)Sa t = at. Hier heiBt [a] endliche monogene oder zyklische
Untergruppe von G.
1st G = [a] fUr ein a E G, so werden die eingefilluten Bezeiehnungen auf G selbst angewandt.
Hilfssatz A. Zu je zwei Zahlen r, q E Z mit q
s, t E Z mit
(11)
r=sq+t,
*- 0
existiert genau ein Paar von Zahlen
O~t~lql-1.
Man nennt t den Rest der Division von r dureh q, weil (11) aueh in der Form gesehrieben
werden kann:
(12)
qr = s + q't
0 ~ t ~ Iql- 1.
Fur t ist aueh die Bezeiehnung Rest von r modulo q gebraueWieh.
Beweis von A. Existenz: Sei t das Minimum alier niehtnegativen ganzen Zahlen der Form
r - nq mit nEZ, etwa t = r - sq. Dann gilt (11), wobei nur noeh t ~ Iql-l naehzuweisen
ist: Ware t > Iq I - 1, so ergabe sieh
(13)
Iql)
t>t-Iql=r-sq-Iql=r- (s+q q;;;O,
was der Wahl von t widersprieht.
Eindeutigkeit: Gilt auBer (11) auehnoeh r == s'q + l' mit 0 ~ t' ~ Iq 1-1, so folgt It-t'l =
= Is - s' I ·1 q I und It - t' I ~ Iq I -1. Ware nun t *- t' oder s *- s', so wiirde aus der ersten
Relation t
lation.
*- t'
und s *- s' sowie It - t' I;;; Iq I folgen, im Widersprueh zur zweiten Re0
Beispiele. 1. Unendliehe monogene Gruppen sind in den StandardzaWbereiehen einfaeh
zu konstruieren. In (R \ 0, .) bilden die Potenzen an einer ZaW a E R \ {I, -I}, in (R, +)
die ganzzahligen Vielfaehen nb einer zaW b E R \ 0 jeweils eine unendliehe mono gene
Untergruppe.
2. Zyklisehe Gruppen lassen sieh besonders leieht im Korper C der komplexen Zahlen angeben, und zwar mit beliebig vorgegebener Ordnung n: Man nehme einfach die Menge der
n-ten Einheitswurzeln, also Wn := {z Eel zn = I}, mit der Multiplikation als Verknupfung.
Dann besteht Wn genau aus den n versehiedenen komplexen Zahlen
(14)
zk:=e
i2~7T
2k7T.. 2k7T
=eos---n-+1'Slllil-'
k
0 1
1
= , , ... , n - .
Fur a:= Zl gilt an = 1 aber ar *- I, falls 1 ~ r ~ n - 1, also ist Wn = [a] zyklisehe Gruppe
der Ordnung n. Jedes Element b E Wn, das wie a die Gruppe Wn erzeugt, nennt man eine
primitive note Einheitswurzel. In W4 etwa sind, wie man leieht naehreehnen kann, Zl, Z3
primitiv, dagegen Zo, Z2 nieht prirnitiv.
0
o Aus der Algebra
6
Bei endlichen Gruppen bestehen starke Einschrankungen fUr die Ordnungen der moglichen Untergruppen: Wir werden sehen, dafl die Ordnung einer jeden Untergruppe die
Ordnung der Gesamtgruppe teilt. Als Vorbereitung hierzu dienen die folgenden Dberlegungen, bei denen zunachst keine Endlichkeit vorausgesetzt wird.
Zunachst gibt jede Untergruppe Anlafl zu zwei ausgezeichneten Aquivalenzklassen in der
Gruppe.
Satz und DefInition B. Sei G eine Gruppe und Heine Untergruppe von G. Sei ferner die
Relation RH aUfG definiert durch
(15)
xRHy:
<==>
xy-I E H,
die Relation HR aUf G definiert durch
(16)
xHRy:
<==>
X-I y E H.
Dann ist
(a) RH .ifquivalenzrelation auf G mit den .ifquivalenzklassen (den Rechtsnebenklassen)
Uz := Hz, z E G;
H R A'quivalenzrelation aUf G mit den Xquivalenzklassen (den Linksnebenklassen)
zU :=zH,zEG;
(b)
(c) die Abbi/dung
(17)
G/RH
---*
G/HR
H
HZ~Z-I
wohldefiniert und bijektiv.
Es sei hier an den Begriffen der Relation erinnert. Eine Relation R auf einer Menge Mist
eine Teilmenge R des cartesischen Produktes M X M. Genau wenn (x, y) E R gilt, sagt
man, x und y stehen in der Relation R, und man schreibt x R y. Eine Relation R auf M
heillt .ifquivalenzrelation, wenn folgende Regeln erftillt sind:
(R)
Refiexivitat:
xRx
(S)
Symmetrie:
xRy=*yRx
Transitivitat: x R y, Y R z =* x R z.
Manchmal schreibt man anstelle von x R yauch x == y(mod R), gelesen x kongruent y
modulo R. 1st R Aquivalenzrelation auf M und a ein [estes Element von M, so ist die
A'quivalenzklasse Ua von a die Menge aller x EMmit a R x. Die Aquivalenzklassen bilden
eine Zerlegung von M, d.h. jedes Element a EM liegt in genau einer Aquivalenzklasse,
namlich in U a • Jedes b E Ua (fUr das dannja U b = U a gilt) heillt ein Reprasentant von Ua .
Die Menge der Aquivalenzklassen wird durch M/R bezeichnet (gelesen M modulo R). Die
Abbildung p : M ....,. M/R, die jedem Element a EM seine Aquivalenzklasse U a zuordnet, ist
die sog. kanonische Projektion von R. Die Menge M/R der Aquivalenzklassen heillt auch
Quotientenmenge von M modulo R.
(T)
Beweis von B. Zu (a): Es miissen die drei Eigenschaften einer Aquivalenzrelation (Reflexivitat, Symmetrie, Transitivitat) nachgepriift werden. Refiexivitat: Diese besagt XRHX,
0.1 G ruppen und Untergruppen
7
d.h. XX-I E H; dies ist wegen XX-I = e und (UG.1) erftillt. Symmetrie: Diese besagt
xRHy => yRHx, d.h. xy-I E H => yx- I E H; dies ist wegen yx- I = (xy-1r l und (UG.3)
erftillt. Transitivitat: Diese besagt xRHy und y RHz => xRHz, d.h. xy-I E H und yz-I E H =>
=> xz- I E H; dies ist wegen xz- I = (xy-I) (yz-I) und (UG.2) erftillt. Fiir die Aquivalenzklasse Uz von z folgt Uz = {xlxRHZ} = {xlxz- I E H} = {xix E Hz} = Hz. Das vorletzte
Gleichheitszeichen folgt mittels (6).
Zu (b): Dieser Nachweis verHiuft analog zu dem von (a).
Zu (c): Zur Wohldefmiertheit ist nachzuweisen, d~ die Vorschrift (17) dasselbe liefert,
werm anstel1e von zein anderes Element z' zur Darstellung der Rechtsnebenklasse Hz verwendet wird. Dies folgt aus den Schliissen
(18)
Hz = Hz'
*=>
zRHz'
*=>
ZZ'-I E H *=> Z-I HRz'-1
*=>
Z-I H = Z'-I H
(man lese von links nach rechts). D~ (17) sUIjektiv ist, folgt, weil z >-+ Z-I eine Bijektion
von G auf sich ist. D~ (17) injektiv ist, folgt wenn man (18) von rechts nach links
D
~~
Bei kommutativen Gruppen gilt natiirlich RH = HR.
In einer nichtkommutativen Gruppe G wird eine Rechtsnebenklasse im allgemeinen nicht
auch Linksnebenklasse sein oder umgekehrt. Der eben bewiesene Teil (c) bedeutet aber,
daB die beiden Sorten von Aquivalenzklassen in bestimmter Weise einander bijektiv zugeordnet sind. Diese Bijektivitat rechtfertigt die folgende
Definition C. Die Untergruppe H von Gist von endlichem Index, wenn G/R H oder,
aquivalent, G/HR endlich ist, und genau in diesem Fall schreibt man
(19)
ind G H:= IG/RHI = IG/HRI
<00.
Mit Betragszeichen urn eine endliche Menge bezeichnen wir generell die Anzahl der Elemente. Der Index ist also die Anzahl der Rechtsnebenklassen (oder der Linksnebenklassen,
da beide Anzahlen iibereinstimmen).
D~ der Index auch bei unendlichem G oder H endlich sein karm, zeigt das folgende
Beispiel 3. Es sei G = R \ 0 mit Multiplikation und H = R+. Hier ist RH = HR =: R (Kommutativitat) und xRy genau dann, wenn xy-I E R+, also wenn x und y dasselbe Vorzeichen haben. Also ist G/R = {R+, R-} und somit derIndex von R+ in R \ 0 gleich 2. D
Satz D (von Lagrange). Sei G endliche Gruppe und H Untergruppe von G. Dann gilt
(20)
IG I = IHI· ind G H,
also
IGI
IG/RHI =IG/HRI =THT'
insbesondere sind Ordnung Lind Index von H Teiler der Ordnung von G.
Beweis. Jede Rechtsnebenklasse Hz ist durch die Abbildung
(21)
H~Hz
X t-----+ XZ
o Aus der Algebra
8
bijektiv auf H bezogen. (Dasselbe gilt ftir jede Linksnebenklasse.) Daraus folgt, daB aile
Rechtsnebenklassen (und aile Linksnebenklassen) dieselbe Anzahl von Elementen enthalten wie H selbst, etwa k Stuck. Sei j := indGH gesetzt. Da G disjunkte Vereinigung vonj
Rechtsnebenklassen ist, besitzt G insgesamt k'j Elemente. Das ist die Behauptung.
0
Folgerung E. Sei G eine endliche Gruppe der Ordnung n und a ein Element von G der
endlichen Ordnung q. Dann ist q Teiler von n und an = e.
Beweis. Nach Satz D und (10) ist n =q 'j, wobeij der Index von [a] in Gist. Nach Defmition von q gilt aq = e, also ist an = aqi = (aqy = ei = e.
0
Laut Defmition ist eine Prirnzahl pEN eine Zahl, die greBer als 1 ist und auBer 1 und p
keine Teiler aus N besitzt. Die Folge der Prirnzahlen beginnt also mit 2, 3, 5,7,11,13,
17,19, ....
Folgerung F. Jede endliche Gruppe G, deren Ordnung eine Primzahl p ist, ist zyklisch
und besitzt keine echte Untergruppe.
Beweis. Dies folgt mit Hilfe von Folgerung E so: Man wahle ein von e verschiedenes Element a von G; dann ist die Ordnung von a nicht 1 und, da sie Teiler von p sein muB,
gleich p. Also ist l[a]1 = p, also wegen [a] ~ G und IGI = p: [a] = G. Eine echte Untergruppe von G kann es nicht geben, da ihre Ordnung nach Satz D Teiler von p sein miiBte.
0
Aufgaben zu 0.1
1. In der Menge Z X Z der Paare ganzer Zahlen definiere man folgende Verkniipfungen T:
a)
b)
c)
d)
(a,
(a,
(a,
(a,
b)
b)
b)
b)
T
T
T
T
(c,
(c,
(c,
(c,
d)
d)
d)
d)
:= (a + c, b + d)
:= (a + c, b + d + 1)
:= (a + c, b + 2d)
:= (a + c, b + lOad).
Welche dieser Verkniipfungen machen Z X Z zu einer Gruppe, welche nicht? 1m ersten Fall gebe man
jeweils das Neutralelement und die Inversenbildung an und entscheide auch, ob die Gruppe kommutativ ist oder nicht.
2. Es sei G eine dreielementige Menge mit den Elementen e, a, b.
fungstabelle so, da~ folgende Eigenschaften gieichzeitig erfUllt sind:
a) e ist Neutralelement;
e
b) jedes x E G besitzt genau ein Inverses;
e e
c) Gist kommutativ;
a ?
d) Gist nicht assoziativ.
b
Man vervollstandige die Verkntipa
b
e
?
e
?
Bemerkung: Aus der eindeutigen Existenz von Neutralelement und Inversem eines Verkntipfungsgebildes folgt also nieht das Assiziativgesetz. Da aus dem Assoziativgesetz und der Existenz eines Neutralelementes aueh nicht die Inversenexistenz gefolgert werden kann [Beispiel: (Z,')], kann im obigen
System der Gruppenaxiome weder (G.l) nach (G.3) weggelassen werden. Es ist aber moglieh, die
Axiome teilweise abzuschwachen; vgl. die folgende Aufgabe.
3. Es sei (G, .) ein Verkntipfungsgebilde, das folgende Axiome erfUllt:
(G'.l) (ab) e = a(be) fUr aile a, b, e E G:
(G' .2) es gibt ein e E G so da~ gilt:
0.2 Homomorphe Abbildungen und Faktorgruppen
9
(i) ea = a flir aile a E G,
(ii) zu jedem a E G existiert ein a* E G mit a*a = e.
Man beweise, da1l. (G, .) eine Gruppe ist.
Hinweis: Man zeige aa* = e durch Betrachtung von a*aa* und leite daraus ab, da1l. e Neutralelement
ist.
4. In der multiplikativen Gruppe R+ der positiven reellen Zahlen betrachte man folgende Teilmengen:
a) H 1 ={a+by'2ER+la,bEQ}.
b) H2 sei die Menge aller rationalen Zahlen r/s, wobei die Zahlen r, sEN hochstens 10 Primteiler
haben.
c) H3 sei die Menge aller rationalen Zahlen r/s, wobei die Zahlen r, sEN hochstens die ersten 10
Primzahlen als Primteiler haben.
Welche dieser Mengen sind Untergruppen von (R+, .), welche nicht?
5. Sei (G, .) Gruppe. Man zeige, da1l. eine nichtleere Teilmenge H S; G genau dann Untergruppe ist,
wenn HH-l £ H gilt. Aus HH-l £ H deduzlere mann HH-l = H.
6. Man beweise, da1l. der Durchschnitt beliebig vieler Untergruppen einer Gruppe G wiederum Untergruppe von Gist.
7. Sei G = [a] eine unendliche monogene Gruppe. Man beweise:
a) 1st n E Z \ 0, so ist [an] unendliche monogene Untergruppe von G.
b) 1st H irgendeine Untergruppe von G, so existiert ein n E Z mit H = [an]. Insbesondere ist jede echte
Untergruppe einer unendlichen monogenen Gruppe selbst unendlich monogen.
8. Es sei G = [a] eine unendliche monogene Gruppe und b = a r E G. Man beweise: Genau dann gilt
[a] = [b], wenn r E {I, -I}.
9. Es sei G = {e, a, ... , a q -
1}
eine zyklische Gruppe der Ordnung q. Man beweise:
a) 1st H Untergruppe von G, so ist die Ordnung u von H Teiler von q.
b) 1st u irgend ein (positiver) Teiler von q, so existiert genau eine Untergruppe H von G der Ordnung
u, namlich H = {e, b, ... , b U - 1}, wobei b:= a k mit k:= q/u. Es gibt also genausoviele Untergruppen
von G wie positive Teiler von q, und aile Untergruppen von G sind zyklisch.
0.2 Homomorphe Abbildungen und Faktorgruppen
Homomorphe Abbildungen sind die strukturvertraglichen Abbildungen von Verkniipfungsgebilden. Wir formulieren hier die entsprechenden Begriffsbildungen fUr Gruppen (obwohl
sie allgemein genauso gelten). Mit G, G', Gil, ... seien hier also stets Gruppen bezeichnet.
Diese werden multiplikativ geschrieben, wenn nichts anderes gesagt ist.
Defmition A. Eine Abbildung h: G ~ G' heif3t:
(i) Homomorphismus, wenn h(x' y) = hex) . hey) filr aile x, y E G;
(ii) Monomorphismus, wenn h Homomorphismus und h injektiv;
(iii) Epimorphismus, wenn h Homomorphismus und h surjektiv;
(iv) Isomorphismus, wenn h Homomorphismus und h bijektiv;
(v) Endomorphismus, wenn h Homomorphismus und G =G';
(vi) Automorphismus, wenn h Isomorphismus und G = G'.
o Aus der Algebra
10
1m allgemeinen sind die Verkniipfungen in G und G' verschieden (obwohl wir sie der Einfachheit halber mit dem gleichen Symbol,,·" bezeichnet haben). Bei (v) und (vi) wird jedoch in G ein und dieselbe Verkniipfung betrachtet. Statt der Substantive in Definition A
werden auch die entsprechenden Adjektive gebraucht, z.B. homomorph, usw .. Der Begriff
des Isomorphismus gibt AnlaB zur
Defmition B. Zwei Gruppen G und G' heif3en isomorph (Symbol: G == G'), wenn ein Isomorphismus h: G ~ G' existiert.
Die einfachen Beweise der folgenden Feststellungen seien dem Leser als Dbungsaufgaben
iiberlassen.
Satz C. Es gilt:
(i) Sind h: G ~ G' und h': G' ~ Gil Homomorphismen, so ist auch h' 0 h: G ~ Gil Homomorphismus.
(ii) 1st h: G ~ G' Isomorphismus, so ist auch h -I : G' ~ G Isomorphismus.
(iii)
G == G;
G == G' => G' == G;
G == G' und G' == Gil => G == Gil.
0
Nach (iii) hat die Isomorphie die Eigenschaften einer Xquivalenzrelation.
Satz D. 1st h: G ~ G' Homomorphismus, so ist h(e) = e' das Neutralelement von G', und
es gilt (h(x)fl = h(X-I) fUr alle x E G. Insbesondere ist Bild h = h(G) eine Untergruppe
von G'.
Beweis. Aus e· e =e folgt h(e) . h(e) =h(e), also (durch Rechnen in G')
h(e) = (h(e)) . (h(e)r l = e'. Entsprechend folgt aus x· X-I = e: h(x)· h(X-I) = h(e) =e',
also h(X-I) =(h(x)r l . Hieraus liest man ab, daB die Menge der Bilder hex) mit x E G die
Untergruppenaxiome (UG.1) bis (UG.3) [0.1] erftillt.
0
Beispiele. 1. Wir betrachten die additive reelle Gruppe (R, +) und die multiplikative Gruppe (R +, .) der positiven reellen Zahlen. Dann defmiert die Exponentialfunktion
(1)
h: R
--->
R+
einen Homomorphismus; denn es gilt flir aIle a, b E R:
(2)
h(a+b)
= ea+ b = eae b = h(a)·h(b).
Dabei geht das Neutralelement beziiglich +, namlich 0, iiber in das Neutralelement beziiglich ., namlich 1. Da h bijektiv ist (Analysis!), ist h sogar Isomorphismus. Der inverse Isomorphismus ist y >-+ In y, die Logarithmusfunktion.
2. 1st a festes Element einer Gruppe (G, .), so defmiert die Vorschrift her) := ar einen
Homomorphismus von (Z, +) in G. Das folgt unmittelbar aus der zweiten Regel in (8)
[0.1]. Die Abbildung h ist injektiv (also ein Monomorphismus), genau wenn die Untergruppe [a] ~ G unendlich monogen ist, und sie ist nicht injektiv, genau wenn [a] zyklisch
0
ist. 1m ersten Fall folgt also: Jede unendliche monogene Gruppe ist isomorph zu (Z, +).
0.2 Homomorphe Abbildungen und Faktorgruppen
11
Nichtkommutative Gruppen defmieren aus sich heraus bereits gewisse nichttriviale Automorphismen:
Satz und Definition E. Sei a ein [estes Element von G. Dann ist die Abbildung
(3)
ha:G-G
x ......... axa- I
ein Automorphismus von G. Jede Abbildung ha dieser Art heij3t ein innerer Automorphismus von G.
Beweis. ha ist homomorph: Es gilt
(4)
ha(xy)
= axya-I = axa -I aya -I = ha(x) ha(y).
h ist injektiv: axa -I
= aya -I
=?
X
=Y (multipliziere von links mit a -I, von rechts mit a).
h ist surjektiv: Zu vorgegebenem z E G sei x = a-I za gewahlt; dann ist x Urbild von z, da
ha(x) = aa- I zaa- I =z. Damit ergibt sich auch noch der
o
Aus E ergibt sich: 1st H Untergruppe von G, so ist ha(H) = aHa- 1 fUr jedes a aus G ebenfalls Untergruppe von G; diese Untergruppen heillen die konjugierten Untergruppen von
H (in G). Diejenigen Untergruppen H, die mit allen ihren Konjugierten zusammenfallen,
sind besonders ausgezeichnet:
Definition und Satz F. Eine Untergruppe H von G heij3t normale Untergruppe oder Normalteiler von G, geschrieben H <l G, wenn eine der [olgenden iiquivalenten Bedingungen
erjUUt ist:
(a) aHa -I
= H jUr aUe
a aus G;
(b) aH = Ha jUr aUe a aus G;
(c) aHa-I S;HjUralleaausG.
Beweis. Die behaupteten Aquivalenzen beweist man leicht mit den in 0.1 aufgestellten
Regeln fUr die Komplexschreibweise. Als Muster sei der SchluB (c) =? (a) vorgeftihrt: Aus
aHa -I S; H folgt durch Multiplikation "von links" mit a -I und "von rechts" mit a unter
Berlicksichtigung von (6) [0.1]: H S; a-IHa. Gilt dies fUr aile a EG, so auch fUr a-I anstelle von a, also folgt H S; aHa -I .
0
Die Bedingung (b) besagt, daB jede Rechtsnebenklasse auch Linksnebenklasse ist, und urn·
gekehrt. FUr normale Untergruppen enWillt also dieser Unterschied, und wir kbnnen einfach von Nebenklassen sprechen; es gilt somit: G/R H = G/HR.
Beispiele. 3. Die beiden trivialen Untergruppen von G sind auch Normalteiler.
4. 1st G abelsche Gruppe, so ist jede Untergruppe H von G Normalteiler, da jeder innere
0
Automorphismus die Identitiit ist.
Weitere Beispiele gewinnt man mit