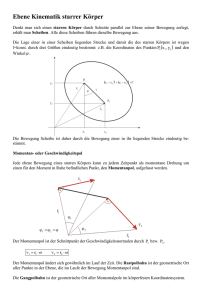
Starre Körper

Einführung in die Physik I
Mechanik der starren Körper
O. von der Lühe und U. Landgraf
Starrer Körper
•
•
•
•
•
•
•
Bislang wurden nur Massen als
Punktmassen idealisiert
behandelt, eine ausgedehnte
Verteilung der Masse spielte eine
unwesentliche Rolle
Definition eines starren Körpers:
Anordnung von i Punktmassen mi
r
r
An den Orten i
i=1…N
Abstände sind zueinander
konstant
Übergang zu kontinuierlichen,
ausgedehnten Körpern
Mechanik der starren Körper
mi
r
ri
2
Freiheitsgrade
•
•
•
Freiheitsgrade: Zahl der
Parameter, die benötigt
werden, um die Lage des
Körpers eindeutig festzulegen
Positionen der N Punktmassen
(3N Koordinatenwerte) minus
der Zahl der Bedingungen für
die konstanten Abstände
Im allgemeinen sind sechs
Angaben ausreichend:
Einzelne Punktmasse
3
Zwei Punktmassen
5
Drei und mehr
Punktmassen
6
– Position des Schwerpunkts
– Rotation um die
Schwerpunktslage
Mechanik der starren Körper
3
Kinematik des starren Körpers
•
•
•
Für die Schwerpunktsbewegung
eines starren Körpers gelten die
kinematischen Gesetze für
Punktmassen
Neu sind Drehungen des starren
Körpers um eine gegebene Achse
„Infinitesimale“ Drehung:
r
dϕ
r
dr
r
r
r r
r
dr = dϕ × r
•
Winkelgeschwindigkeit:
r
r
dr r r
dϕ r r r
= v (r ) =
×r = ω×r
dt
dt
r
ω
r
v
r
r
Siehe auch: Kinematik 1 Folie 19
Mechanik der starren Körper
4
Dynamik des starren Körpers
•
r
Rotationsenergie – eine
Rotationsbewegung enthält die
Summe der kinetischen Energien
der einzelnen Massenpunkte
1
2
= ∑ mi ⋅ (v(r⊥ ,i ))
i =1 2
ω
r⊥
N
Erot
1 2 N
2
= ω ∑ mi ⋅ (r⊥ ,i )
2
i =1
•
Senkrechter Abstand r⊥ einesr
Massenpunkts von der Achse ω
r r
wird durch das Kreuzprodukt ω × r
vermittelt
Mechanik der starren Körper
r
v (r⊥ )
r
ω
r⊥
5
Dynamik des starren Körpers
•
r
Integralform der Rotationsenergie:
ω
– Massendichte ρ
– „infinitesimales Volumenelement“ dV
– Infinitesimales Massenelement ρ dV
Erot
1 2 2
= ω ∫ r⊥ ⋅ ρ ⋅ dV
2 V
•
Die Dichte ρ kann ortsabhängig sein
•
Der Ausdruck mit dem Integral ist
eine Eigenschaft des Körpers und
der Lage der Rotationsachse
Mechanik der starren Körper
r⊥
ρ ⋅ dV
6
Dynamik des starren Körpers
•
•
Analogie zur kinetischen Energie:
bei der Rotationsenergie spielt
der Ausdruck mit dem Integral
bezüglich der Rotationsachse die
Rolle der Masse bei der
kinetischen Energie
Trägheitsmoment J
Erot =
1 2 2
ω ∫ r⊥ ⋅ ρ ⋅ dV
2 V
1 2
v ⋅m
2
1
= v 2 ∫ ρ ⋅ dV
2 V
Ekin =
J = ∫ r⊥2 ⋅ ρ ⋅ dV
V
•
Ein Massenelement trägt umso
mehr zum Trägheitsmoment bei,
je weiter es von der Achse
entfernt ist
Mechanik der starren Körper
7
Dynamik des starren Körpers
•
•
Beispiel für Trägheitsmoment:
Stab mit konstanter Dichte und der
Länge L
Rotationsachse durch das
Stabende:
L
J = ∫ r⊥2 ⋅ ρ ⋅ dV = ρ ⋅ A∫ x 2 ⋅ dx =
0
V
L
A
x
1
1
ρ ⋅ A ⋅ L3 = ML2
3
3
L
•
A
Rotationsachse durch die
Stabmitte:
L2
1 3
1
J = 2 ρA ∫ x ⋅ dx = 2 ρA ⋅
L =
ML2
3⋅8
12
0
x
2
Mechanik der starren Körper
8
Dynamik des starren Körpers
•
•
•
Satz von Steiner:
„Das Trägheitsmoment eines
Körpers bezüglich einer beliebigen
Drehachse setzt sich zusammen
aus dem Trägheitsmoment
bezüglich einer dazu parallelen
Achse durch den Schwerpunkt und
dem Trägheitsmoment der
Gesamtmasse“
a
S
J = JS + M ⋅ a2
Beispiel Stab:
2
1
3
1
⎛L⎞
J Ende = J Mitte + M ⋅ ⎜ ⎟ =
ML2 + ML2 = ML2
12
12
3
⎝2⎠
Mechanik der starren Körper
9
Dynamik des starren Körpers
•
•
Drehmoment T:
Analogon zur Kraft bei der Translation
Erhöht oder erniedrigt die
Rotationsenergie
r
T
r
r
r
F
r
r
• Eine Kraft F greift an einem Punkt r ,
ausgehend vom Drehpunkt an
•
Das Drehmoment ist ein Vektor, der
sowohl auf dem Ortsvektor des
Angriffspunkts als auch auf dem
Kraftvektor senkrecht steht
Mechanik der starren Körper
r r r
T = r ×F
10
Dynamik des starren Körpers
•
•
•
Drehimpuls L:
Analogon zum linearen Impuls
Für einen ausgedehnten Körper
ergibt sich der Drehimpuls aus
der Summe der Drehimpulse
seiner Bestandteile
Der Drehimpuls wird bestimmt
relativ zu einer Drehachse
r
ω
r⊥
r
v (r⊥ )
r
L=
r r
m
⋅
r
∑ i i × vi
N
i =1
=
r r r
m
⋅
r
∑ i i × (ω × ri )
N
i =1
•
Für einen Körper, der um eine
Symmetrieachse rotiert, gilt
r r N
L = ω ∑ mi ⋅ r⊥2,i
i =1
Mechanik der starren Körper
11
Dynamik des starren Körpers
•
Ein kräftefreier Körper kann ohne Einwirkung von außen seinen Rotationszustand nicht verändern (Reaktionsprinzip!)
•
Ein kräftefreier Körper rotiert um eine Achse
durch seinen Schwerpunkt
•
Man kann die Trägheitsmomente eines
Körpers bezüglich dreier Rotationsachsen
durch den Schwerpunkt bestimmen. Die
Komponenten lassen sich in Form eines
Tensors anordnen (Trägheitstensor)
•
Der Drehimpuls ist in der Regel nicht
parallel zur Drehachse
Mechanik der starren Körper
r
L
r
ω
z
y
x
⎛ J xx
⎜
J = ⎜ J yx
⎜J
⎝ zx
J xy
J yy
J zy
J xz ⎞
⎟
J yx ⎟
J zz ⎟⎠
r
r
L = Jω
12
Trägheitstensor
•
•
Rechenvorschrift, allgemeines
Koordinatensystem (rechts)
Wählt man ein geeignetes, and den
Symmetrieachsen des Körpers
ausgerichtetes Koordinatensystem
(„Hauptachsensystem“), dann
verschwinden die Nichtdiagonalterme
J xx =
∑ m (y
J yy =
∑ m (x
J zz =
2
i
+ zi2
)
2
i
+ zi2
)
2
2
m
x
+
y
∑ i i i
)
N
i =1
i
N
i =1
N
i
(
i =1
N
J xy = J yx = − ∑ mi xi yi
i =1
⎛ J xx
⎜
J=⎜ 0
⎜ 0
⎝
0
J yy
0
0 ⎞
⎟
0 ⎟
J zz ⎟⎠
N
J xz = J zx = − ∑ mi xi zi
i =1
N
J yz = J zy = − ∑ mi yi zi
i =1
Mechanik der starren Körper
13
Dynamik des starren Körpers
•
Der Drehimpuls ist eine Erhaltungsgröße
•
Nur äußere Drehmomente können den Drehimpuls eines
Körpers ändern
•
Innere Kräfte können den Drehimpuls nicht ändern
•
Ohne äußere Kräfte bleiben Betrag und Richtung des
Drehimpuls erhalten
•
Bewegungsgleichung der Rotation
Mechanik der starren Körper
r
dL r& r
= L =T
dt
14
Gerthsen
Physik
Mechanik der starren Körper
15
Gleichgewicht und Bewegung
•
Ein starrer Körper ist im
Gleichgewicht, wenn die Summe
der auf ihn einwirkenden Kräfte
und Drehmomente verschwindet
r
F =0
r
T =0
– Schwerpunktsbewegung konstant
– Drehbewegung konstant
•
r
r1
Hebelgesetz:
– Die Kräfte an den Enden
verhalten sich umgekehrt zu den
Längen der Hebelarme
r r
r r
r1 × F1 = − r2 × F2
r1
F
= 2
r2
F1
Mechanik der starren Körper
r
r2
r
F1
r
F2
r r
F1 + F2
16
Schwerpunkt
•
•
Ein starrer Körper ändert seine
Drehbewegung nicht, wenn alle
Drehmomente bezüglich des
Schwerpunkts sich aufheben
Der Schwerpunkt ergibt sich aus
der räumlichen Verteilung der
Masse
r
m
⋅
r
∑ i i
n
r
rS =
i =1
n
∑m
i =1
r
rS =
1
=
M
n
r
∑m ⋅r
i =1
i
i
i
r
r r
(
)dr
r
⋅
ρ
r
∫
V
r r
1 r
(
)dr
r
⋅
ρ
r
r r =
∫
M
V
∫ ρ (r )dr
V
•
Ein starrer Körper im Gravitationsfeld muss im Schwerpunkt
unterstützt werden, damit die vom
Feld ausgeübten Drehmomente
ausgeglichen sind
Mechanik der starren Körper
17
Gleichgewichte
•
Stabiles Gleichgewicht:
– Kehrt nach einer kleinen
Auslenkung in die Ruhelage
zurück
•
Labiles Gleichgewicht:
– Jede noch so kleine
Auslenkung wird vergößert
•
Indifferentes Gleichgewicht:
– Jede Auslenkung führt in ein
neues Gleichgewicht
Mechanik der starren Körper
18
Gleichmäßig beschleunigte Rotation
•
•
Walze rollt auf schiefer Ebene (ohne zu gleiten)
r r r
Drehmoment
T = r×F
T = r ⋅ sin α ⋅ M ⋅ g
r ·sin α
r
•
Trägheitsmoment der Walze
– Auflagelinie ist Drehachse
– Steinerscher Satz
J = JS + M ⋅ r
•
Bewegungsgleichung
F = M·g
2
r r&
r
T = L = Jω&
(
α
)
M ⋅ g ⋅ r ⋅ sin α = J S + Mr 2 ⋅ ω&
•
Bewegung des Schwerpunkts
Mechanik der starren Körper
aS = r ⋅ ω& = r
M ⋅ g ⋅ r ⋅ sin α
JS + M ⋅ r2
19
Gleichmäßig beschleunigte Rotation
•
Trägheitsmomente:
•
Vollzylinder
1
J S = Mr 2
2
•
Hohlzylinder (dünnwandig)
J S = Mr 2
•
Kugel
2
J S = Mr 2
5
Mechanik der starren Körper
20
Drehschwingungen und Pendel
•
Schwingung eines homogenen Stabs
•
Drehmoment und
Bewegungsgleichung
T = − M ⋅ g ⋅ a ⋅ sin ϕ
≈ − M ⋅ g ⋅ a ⋅ϕ
= J ⋅ ω& = J ⋅ ϕ&&
ϕ (t ) = ϕ 0 ⋅ sin (ϖt )
•
•
Lösung
ϖ =
Mechanik der starren Körper
S
M ⋅ g ⋅a
J S + M ⋅ a2
ϖ =
lred
ϕ
-M·g
M ⋅ g ⋅a
=
J
Vergleich mit Fadenpendel
(„reduzierte Länge“)
a
g
lred
=
M ⋅ g ⋅a
J S + M ⋅ a2
J S + M ⋅ a2
=
M ⋅a
21
Kreisel
•
Rotationssymmetrischer Körper
•
„Figurenachse“ durch den
Schwerpunkt
•
Kräftefreier Kreisel:
S
– Unterstützt im Schwerpunkt
– Drehachse gleich Figurenachse
•
Allgemein:
– Drehachse nicht Figurenachse
– Nutationsbewegung
– Äußere Kräfte Präzessionsbewegung
Mechanik der starren Körper
S
22
Gerthsen
Physik
Mechanik der starren Körper
23