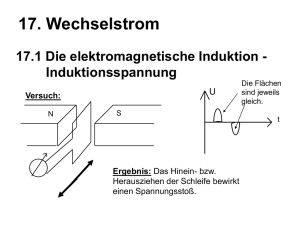
Analysis 1+2 - Zusammenfassung

Analysis
Zusammenfassung
Lernhilfe
verfasst anhand des Skripts Analysis I/II von U. Stammbach
von Norman Juchler, D-MAVT
[email protected]
WS/SS 2003/4
Bemerkungen:
 Die Zusammenfassung ist mit Hinweisen zur verbreiteten Formelsammlung
„Formeln und Tafeln“ (Orell Füssli Verlag) versehen.
 Lasst davon ab, selber eine so umfangreiche Zusammenfassung zu schreiben…
 Bei Fragen kontaktiert mich per Mail!
 Viel Erfolg im Studium!
1
Funktionen
Definition:
Eine Folge von reellen Zahlen ist eine Abbildung von N (oder N 0 ) in die reellen Zahlen.
1
c
an 1  (a n 
),n  1
2
an
sin( n 2 )
an  2
n 5
Beispiele:
rekursiv:
explizit:
Definition:
Eine Folge a1 , a2, ... heisst Nullfolge, falls es zu jeder noch so kleinen Zahl   0 ein m gibt, so
dass für alle Glieder gilt: amk   .
Schreibweise:
lim a
n 
n
0
Daraus folgen die Begriffe Divergenz und Konvergenz.
Definition:
Eine Folge a1 , a 2, ...a k ...a n heisst beschränkt, wenn ihr Bild ganz in einem endlich breiten,
waagrechten Parallelstreifen enthalten ist. Schranken: c1 ≤ x ≤ c2
Definition:
monoton wachsend: an+1  an
Satz:
Ist eine Folge |a| monoton wachsend oder fallend und beschränkt, so ist sie konvergent.
Bemerkung:
Konvergenz weist man nach, indem man Wachstumsverhalten und Beschränktheit untersucht:
Beispiele:
Definition:
an+1  an
monoton fallend:
(strikt…)
 Wachstumsverhalten:
monoton wachsend, fallend?
 Beschränktheit:
mittels Limes oder beschränkter Hilfsfolge (TRICKS!!!).
Wichtige Folgen: (vgl. FB S32)
1 1 1
1
   
1! 2! 3!
n!
n 1
führt zu e = lim 1  n1  für n  
n 1
führt zu
n 1
Harmonische Reihe, nicht konvergent!

an  1 

a n 1 

sn  1 
1 1
1
   
2 3
n

sn  1 
1 1 1
1
       ( 1) n
2 3 4
n 1
1
c
(a n 
)
2
an
n
n 
c für n  
Alternierend harmonische Reihe, konvergiert
Eine Folge folgender Form heisst geometrische Folge:
Explizit:
an  aq n mit Anfangsglied a und Faktor q.
 Konvergenz für q  1 , Divergenz für q  1
2
Rekursiv: a n 1  a n q
Definition:
Reihe sn   ai , also die Summe aller Glieder einer geom. Folge  geometrische Reihe.
i 1
Beispiel:
Geometrische Reihe mit q  1 : Rekursiv definiert durch s0  a1 , sn1  sn  x n1
Aus xsn  s n  x n1  a1 folgt: sn  1a1q
Satz:
Falls eine Folge konvergiert, dann ist der Limes eindeutig.
lim a n  bn   a  b


n 
lim a n  bn   a  b
n
a  a
lim  n   bn  0
n


n
 bn  b
Jede monotone beschränkte Folge konvergiert. Für Funktionen gelten dieselben Rechenregel
lim c  a n   c  a

4

Beispiel:
 2n 2 
2


  lim 
lim  2
 24

2
n  n  3

 n   1  3 / n 
Beispiel:
lim
Definition:
x 0
4
sin x
sin x
sin 2 x
sin x
sin x
1
1
 lim
 1 , lim 2
 lim
 lim
 lim
 (Fkt. ist gerade!)
x

0
x

0
x

0
x

0
x

0
x
x
x (1  cos x)
x
x
1  cos x 2
Eine Funktion oder Abbildung von der Menge A in die Menge B ( f : A  B ) ist eine
Vorschrift, die für jedes Element x  A ein Element f ( x)  B festlegt: f : x  f ( x) .
W ( f )  f ( x) x  D( f ) heisst Wertebereich.
D(f) heisst Definitionsbereich.
Beispiel:
Schreibweise: f : x  sin x ; f : R  R ; D ( f )  R , W ( f )  [ -1,  1]
Bemerkung:
Symmetrieüberlegungen ersparen oft viel Arbeit (Tangenten, linker, rechter Grenzwert…)
Definition:

Gerade Funktion
f ( x)  f ( x) Symmetrie an der y-Achse

Ungerade Funktion
f ( x)   f ( x) Symmetrie am Nullpunkt

Wachstumsverhalten
Monoton wachsend, fallend?
Die elementare Funktionen oder grundlegende Funktionen sind: Potenz-, Polynom-,
Rationale, Trigonometrische Exponential- und Logarithmusfunktionen.
Definition:
Graph einer Funktion D( f )  R, D(f)  R D(f) ist die Menge der Punkte (x, y) mit y = f(x).
Definition:
Stetigkeit. Die Funktion f(x) ist stetig im Punkt ξ, wenn für jede Folge (xn) in D(f) mit
lim xn   gilt: lim f ( x )  lim f ( x )  f ( )  linker und rechter Grenzwert sind gleich.
n
x 
x 
f(x) heisst stetig schlechthin, wenn f in jedem Punkt a von D(f) stetig ist.
3
Satz:
Sämtliche Elementarfkt. und die aus ihnen durch Addition, Subtraktion, Multiplikation,
Division & Zusammensetzung gebildeten Fkt. sind in ihrem Def’bereich stetig. (Polstellen 
D(f )!)
Satz:
Zwischenwertsatz. Es sei f : x  f ( x) eine auf a, b stetig Funktion. Es sei m irgendein
Wert zwischen f(a) und f(b). Dann gibt es (mindestens) ein  mit f ( )  m .
„Graph schneidet im Intervall y  m “  „Binärer Suchalgorithmus“ ≈ Intervallschachtelung
Bemerkung:
Mit Koordinatentransformation lässt sich das Wesentliche einer Funktion einfach erkennen.
f1 : x  f ( x  a)
Verschiebung um a in Richtung der negativen x-Achse
f 2 : x  f ( x)  b
Verschiebung um b in Richtung der positiven y-Achse
f 3 : x  f (cx), c  0
Stauchung in Richtung der x-Achse. (Dehnung: c  0 )
f 4 : x  d  f ( x), d  0 Streckung in Richtung der y-Achse (Stauchung: d  0 ).
f5 : x 
Wo f (x) NST hat, hat f 5 ( x) Pole, „Spieglung“ um y  1 : 0,1 auf
1
f ( x)
der y-Achse dem Intervall 1,  entspricht und vice versa.
f 6 : x  f ( 1x )
Das Verhalten von f (x) für x >1 wird ins Verhalten von f 6 ( x) für
0 < x < 1 „gespiegelt“
Definition:
Eine Funktion f (x) heisst injektiv falls:  x1  x2  D(f) gilt f (x1) f (x2). (auch eineindeutig)
Stetige Fkt. f ist genau dann injektiv, wenn sie in D(f) strikt monoton wachsend/ fallend ist.
Definition:
Inverse Funktion. Ist eine Funktion f (x) eine injektive Funktion, so gilt für ihre Inverse f 1 :
f 1 ( y )  das eindeutig bestimmte x mit f(x)  y
Bemerkung:
 x  x
Es gilt (trivial): f 1  f x   f f
1
Folgend einige Eigenschaften der Inversen, die das „Handwerk“ erleichtern.

f (x ) und f
1
( x) sind zu y  x symmetrisch.

Gerade Funktionen durch Einschränken von D(f) injektiv machen.

Man beachte die Definitions- und Wertebereiche von f
1
( x) , insbesondere bei den
zyklometrischen Funktionen (betrachte dazu Formelblatt im Anhang)!
Definition:
Zu einer im Intervall c,   definierten Funktion f (x) ist g (x ) eine Asymptote von f (x) für
x   wenn gilt lim ( f ( x)  g ( x))  0
x 
Beispiel:
f ( x) 
2x  1 2x  2  3
3

 2
, g ( x )  2 stellt eine Asymptote für f(x) dar.
x 1
x 1
x 1
4
Definition:
Differenzenquotient: f ( x0  h )  f ( x0 ) Differenzialquotient.
h
Definition:
Differenzierbarkeit. Eine Fkt. x  f (x ) heisst differenzierbar an der Stelle x0  D( f ) , falls
df
der Differenzialquotient dx ( x0 )  lim
ho
f ( x0  h)  f ( x0 )
h
f ( x 0  h)  f ( x 0 )
df
x 0  lim
dx
h
h o
existiert. Dann ist f (x ) auch stetig in x0 .
Eine Funktion x  f (x) ist differenzierbar, wenn jede Stelle x0  D( f ) differenzierbar ist.
Bemerkung:
Der Grenzwert von links muss mit dem Grenzwert von rechts übereinstimmen  nicht jede
stetige Funktion ist differenzierbar! In der Differenzierbarkeit ist die Stetigkeit enthalten!
Definition:
Die Ableitung (Derivierte) ist die Funktion f ' mit D( f ' )  D ( f ) der diff’baren Funktion f(x).
Satz:
Rechenregeln zur Differenziation (Vgl. FB S36): Linearität der Ableitungsfunktion,
Produktregel, Quotientenregel, Kettenregel.
Satz:
Ableitung der Inversen. Es gilt f ( f 1 ( x )) ≡ x und daraus folgt f ' ( f 1 ( x)) ( f 1 )' ( x) ≡ 1 .
( f 1 )' ( x ) =
Beispiele:
1
1
f ' ( f ( x ))

dx
1
( y) 
dy
dy
( x)
dx
d arcsin
1
1
( x)  g' ( x) 

dx
cos(arcsin x )
1  x2
f ( x)  e x 
d arctan
( x )  h' ( x ) 
dx
1
1
cos2 (arctan x )

1
1 x2
d log
1
1
1
( x) 


dx
f ' (log( x )) f (log( x )) x
d2 f
zweite Ableitung  f '' x   f ' ' x  
Definition:
Eine Funktion heisst glatt (unendlich oft differenzierbar) wenn sie n-mal differenzierbar ist.
Definition:
konvex (nach oben/ links gekrümmt)
dx 2
x 
dn f
( x)
dx n
Beispiel:

konkav (nach unten/ rechts gekrümmt) 
n-te Ableitung
f (n) 
f ' ' x   0 , Sekante oberhalb der Kurve.
f ' ' x   0 , Sekante unterhalb der Kurve.
 Übergang von konvex zu konkav und umgekehrt.
Wendepunkt
i.A. f ' ' ( x0 )  0 und

Terrassenpunkt
5
f ' ' ' x0   0
f ' x0   f ' ' ( x 0 )  0 und
f ' ' ' x0   0 von G(f)
Bemerkung:
Im Wendepunkt x 0 muss das Vorzeichen von y’ wechseln! Dies ist auch in Polstellen möglich!
Beispiel:
Wachstumsverhalten:
f ' ( x)  0
Extremalstellen:
f ' ( x 0 )  0 und
f ' ' x 0   0
lokales Maximum
f ' ( x 0 )  0 und
f ' ' x 0   0
lokales Minimum
Definition:
f ' ( x)  0
f ist wachsend
f ist fallend
Linearisieren. Unter einer Linearen Ersatzfunktion (~Differential) versteht man folgende
Formel: x  f ' ( x0 )( x  x0 )  f ( x0 ) . Sie stellt die Tangente von f in ( x0 ) dar.
Bemerkung:
Betrachtet man den Vergleich  ( x)  f ( x)  ( f ' ( x0 )( x  x0 )  f ( x0 )) zw. Kurve und Tangente,
so folgt:  ( x)  o( x  x0 ) für x  x0 ! In Worten: Tangente ist gute (lokale) Approximation.
Führt man ein neues Koord’system ein mit Ursprung in ( x0 , f ( x0 )) und Achsen dx, df, so folgt:
df : dx  f ' ( x0 )  dx  df (dx )
Tangente (= lin. Ers.fkt.):
 ( x) :
Beispiel:
f  f ( x)  f ( x0 ) ~ df
Linearisieren: Gesucht sei die lineare Ersatzfunktion für f(x) = sin x in x0 = π/3.
x  12 ( x  3 ) 
Beispiel:
3
2
 12 x 

3
2
 6

Fehlerrechnung: Gesucht sei das Volumen V einer Kugel aus dem gemessenen (mit Fehler
behaftetem) Durchmesser x: Es gilt f ( x )  V ( x ) 
Fehler: df  dV 
Definition:
( Differential!)
4
3
2x 3 . Daraus folgt für den absoluten
  dx  2 2x 2 dx . Und für den relativen Fehler:
4 3 x 2
3 2 2
dV
V
 3 dxx
Lokales Maximum: Eine Funktion f : x  f ( x ) mit D(f) besitzt in   D(f) eine lokale
Maximalstelle, wenn es ein Intervall (c, d) gibt mit c <  < d, so dass für alle x aus D(f) gilt
f(x) ≤ f(  ). Der Wert f(  ) heisst dann ein lokales Maximum von f.
Analog: lokales Minimum/lokale Minimalstelle. Lokales Extremum/ Extremalstelle.
Definition:
Es sei f : x  f ( x ) eine auf dem Intervall [a, b] def. Funktion. Man sagt, x0  [a, b] sei eine
globale Maximalstelle, wenn für alle x  [a, b] gilt g(x0) ≥ g(x). Unterscheide: lokal, global.
Satz:
Bemerkung:
Potentielle Kandidaten für eine lokale Extremalstelle x0 einer Funktion g(x) können sein:

Randpunkte des Definitionsintervall

Polstellen

Punkte x0 wo gilt g’( x0 ) = 0
Nicht in jedem Punkt, wo g’( x0 ) = 0 gilt, ist Extremum! ( 2. Ableitung!)
6
Definition:
Ist U eine Teilmenge des n-dimensionalen euklidischen Raums R n , dann nennt man U abgeschlossen, falls gilt: Für jedes x des R n ausserhalb von U gibt es eine reelle Zahl ε > 0, so dass
jeder Punkt y des R n , dessen Abstand zu x kleiner ist als ε, ebenfalls ausserhalb von U liegt.
Definition:
Eine Menge S heisst beschränkt, wenn sie in einem endlichen Intervall liegt.
Definition:
Kompakte Mengen im eukl. Raum R n sind abgeschlossen und beschränkt. Z.B. D = [0,1]
Satz:
Jede auf einer kompakten Menge A definierte stetige Funktion f : A  R hat ein globales
Maximum und ein globales Minimum.
Satz:
Satz von Rolle. Es sei f : x  f ( x) eine differenzierbare Funktion mit f x1   0  f x2 
x1  x2 . Dann gibt es mindestens ein  , x1    x 2 mit f ' ( )  0 .
Satz:
Mittelwertsatz der Differenzialrechnung. Es sei f : x  f ( x) eine im Intervall x1 , x2  def.
diff’bare Fkt. Dann gibt es (mindestens) ein  , x1    x 2 mit f ' ( ) x 2  x1   f x 2   f x1  .
0

Satz:
Regel von Bernoulli – Hôpital. Für Grenzwertberechnung von Brüchen der Form . und
0

f x 
f ' x 
lim
 lim

Vgl
FB
S35
na g x 
na g ' x 
Bemerkung:
Rechenregeln und Eigenschaften von Exponential- und Logarithmusfkt.: FB S30
Definition:
Hyperbolische Funktionen: Definitionen, Graphen und Sätze  FB S31
Sinus hyperbolicus
definiert durch sinh x 
Cosinus hyperbolicus definiert durch cosh x 
1
2
1
2
e
e
x
x
 ex 
cosh 2 ( x )  sinh 2 ( x )  1
 ex 
sinh' ' ( x )  cosh' ( x)   sinh( x)
Eulersche Formeln: sin( x)  1i sinh( ix ) , cos( x )  cosh( ix ) .
Definition:
Grössenordnung einer Funktion. Vergleich von 2 Funktionen für x → ∞, oder x → a  .
f(x) ist von kleinerer Grössenordnung als g(x) für x   oder x  a  wenn gilt:
lim
x 
f ( x)
f ( x)
 0 bzw. lim
 0  f (x) << g(x) bzw. f ( x )  o( g ( x )) für x  
x a g ( x )
g( x)
7
Bemerkung:
Exponentialfunktionen verhalten sich extremer als Potenzfunktionen und diese extremer als die
Logarithmusfunktionen. log x   x  e cx ,   0, c  0
Beispiele:
x k  o (e x )
für x   und k  R \0)
log x  o( x k )
für x   und k > 0
e  x  o( x  k ) für x   ( e  x strebt stärker gegen 0!)
Beispiele:
Darstellung von ebenen Kurven. Arten: parametr.  implizit  explizit  paramtr.
Hyperbel mit Halbachsen a und b und Mittelpunkt im Ursprung

Parameterdarstellung

Implizite Darstellung
FB S39
a2

y2
b2
1
 1,
D f 1    ,a   a, 
x2
a2
 1,
D f 2    ,a   a, 


Tangente im Punkt P: OR  r t   sr t ,    s  

wobei r (t )  ( x (t ), y (t ))


Normale im Punkt P: OR  r t   sn t ,    s   ,
wobei n(t )   y t , x t 
Explizite Darstellung
Krümmung k(t):
Beispiel:
x2
x2
a2

Satz:
t  r t   a cosh t , b sinh t ,    t  
k t  
 f : x  y  b
 1

f : x  y  b

 2
yx  yx
x
2
 y
Krümmung eines Kreises: k (t ) 

3
2 2

y' '
1  y' 
3
2 2
=
d
ds
k > 0  α nimmt zu  konvex
k < 0  α nimmt ab  konkav
1
r
x

 y 2 2 1  y '2 2

yx  yx
y' '
3
3
2
Definition:
Krümmungskreis. Kreis, der Kurve in P am Besten approximiert:
Satz:
Evolute. Durchläuft man die Kurve K, so beschreibt der Krümmungsmittelpunkt M 0 eine
Kurve K’, die Evolute der Kurve K. Krümmungsmittelpunkt  t , t  bzw. M  (u, v ) des
Krümmungskreises bezüglich P(t) bzw. P(x). Es gilt:


1 n (t )
OM 0  r (t ) 
 , daraus folgt:
k (t ) n (t )
Beispiel:
 t   x  y
x 2  y 2
xy  xy
x 2  y 2
 t   y  x
xy  xy
u x
f ' x 
2
1   f ' x 
f ' ' x 


1   f ' x 
v  f x  
f ' ' x 
2

Polarkoord’   r ( )   f ( ) cos , f ( ) sin   : Bernoulli-Spirale. f ( )    Ce k C, k  0 .
Eigenschaften:

ω konstant für alle φ.

Tangenteneigenschaft, siehe Abb.

Evolute ist die um + 90° gedrehte Bernoulli-Spirale.
8
Integralrechnung
Definition:
Beispiel:
Gegeben eine Funktion f : x  f ( x ) und ein im Def’bereich von f liegendes Intervall [a, b].

Bilde Teilintervalle in [a, b] durch endlich viele Punkte a = x0 < x1 < … < xn-1 < xn = b.

Wähle Zwischenpunkte ξk, k = 1, 2, …, n. Die Feinheit ist definiert durch max xk  xk 1

Riemann’sche Summe:
f (1 )x1  ...  f ( n )xn  k 1 f ( k )xk

Riemann’sches Integral:


b
0
x 2dx  lim
n

1
n
n
b
a
f ( x )dx  lim k 1 f ( k )xk (Feinheit strebt gegen null.)
n
b    n2 b   ...   nn b 
2
2
2

b
n
 lim 12  2 2  ...  n 2  bn3 , mit
3
n
12  ...  n 2  16 n( n  1)( 2n  1) (vgl. FB S32) folgt
Bemerkungen:

b
0
x 2 dx 
b3
3
Rechenregeln für bestimmte und unbestimmte Integrale: Siehe FB S41, 42.
a
Weiter gilt für ungerade Integranden:
und für
gerade Integranden:


a
a
a
f ( x)dx  0
a
f ( x)dx  2 f ( x)dx
0
Satz:
Mittelwertsatz der Integralrechnung: Es existiert ξ in [a, b] mit (b  a ) f ( )   f ( x )dx
Bemerkung:
Für Gebietsintegrale oder Volumenintegrale gehen f(ξ) und (b - a) in höhere Dimension über…
Beispiel:
Betrachten der Parabelfläche im Intervall [0, b]: f ( )   2 
Satz:
Hauptsatz der Infinitesimalrechnung. Die Ableitung eines best. Integrals über eine stetige
b
a
Funktion f nach der oberen Integrationsgrenze ist:
Definition:
b3
3b
  b 3/3
x
d
dx a
 f (t )dt  f ( x)
Für eine Stammfunktion F : x  F ( x ) zu f(x) muss gelten: F’(x) = f(x)
Ein bestimmtes Integral hat, ein unbestimmtes Integral hat keine Integrationsgrenzen
b
Satz:
Dank dem Hauptsatz gilt für ein bestimmtes Integral:
 f (t )dt  F (b)  F (a )  F ( x)
b
a
a
Bemerkung:
Stammfunktionen: FB ab S 43, Blatt.
I ( y, z ) 

b
a
Rechenregeln für best. Integrale: FB S 41
v1
dx  v1 (b, y , z )  v1 (a , y , z )
x 9
Bemerkung:
Wichtig ist auch:
Methode:
Methode der partiellen Integration ist die Umkehrung der „Produktregel“:  u' vdx  uv   uv' dx
Beispiele:
e
x
cos(bx )dx  1 ex cos(bx)  ab  ex sin( bx)dx   1 ex cos(bx)  ab
e
1
a
x

sin( bx)  ab  ex cos(bx )dx …
 log xdx   1 log xdx  ...
 f ux  u' xdx   f z dz
Methode:
Methode „Substitution“ ist Umkehrung der „Kettenregel“:
Bemerkung:
Substituieren einer Funktion u(x) lohnt sich, falls der Integrand den Faktor u’(x) enthält.
z u ( x )
Substitution in zwei Richtungen möglich… Achtung: Integrationsgrenzen anpassen!
Beispiele:
Bemerkung:
 sin
n
x cos xdx
 u( x )  sin x
u' ( x )  du / dx  cos x
  u n du

1  x 2 / a 2 dx
 x(t )  a sin t
dx  x  dt  a cos t  dt
  a cos 2 t  dt

1  x 2 dx
 x(t )  sinh t
dx  x  dt  cosh t  dt

 a cosh
2
t  dt
Periodische Integranden: Ist das Integrationsintervall gerade so gross wie das
Periodizitätsintervall einer mit Mittellinie y = 0 gegebenen Funktion, so ist das Integral immer
gleich Null.
 /2
Beispiele:
Anwendung: Rekursion für I n  
Methode:
Bei rationalen Fkt. lohnt sich oft die Anwendung der Methode der Partialbruchzerlegung.
Beispiel:
x
Methode:
Flächenberechnung für parametrisierte, vektorwertige Funktionen. Es gilt: I   y (t ) x (t )dt .
0
2
dx
B 
 A
 

dx
 6x  5
 x  5 x 1
sin n x  dx (siehe Blatt!)  Formel von Wallis für π!
 A, B  ...
tB
tA
Heuristische Herleitung: dI  y (t )dx  y (t ) x (t )dt .
Laufrichtung der Kurve beachten! Wird die Kurve K mit wachsendem t von rechts nach links
durchlaufen, d.h. gilt x (t ) < 0  negative Fläche  unterschiedliche Bereiche  Beträge.
Methode:
Berechnung einer Sektorfläche:
IS 
10
 xt  y t   x t  y t dt
tB
1
2 t
A
[
 xdy  ydx  ]
tB
1
2 t
A
ACHTUNG:
Integral liefert
positive Werte, wenn Sektorfläche links von Kurve liegt,
negative Werte, wenn Sektorfläche rechts von Kurve liegt.
2
1
2 0

(ab cos 2 t  ab sin 2 t )dt  ab
Beispiel:
Ellipsenfläche: F 
Methode:
Sektorfläche für Polarkoordinaten. Mit x( ), y( )   ( ) cos ,  ( ) sin   : I S 
Methode:
Berechnung der Bogenlänge einer Kurve. Es gilt für die verschiedenen Darstellungen:
tB
x (t )
s 
parametrisiert:
s AB 
 2d

  y (t )  z (t ) dt   r (t ) dt .
2
2
tA
explizit (eben):

tB
2
B
A

B
1
2 
A
tA
xB

1   f ' ( x ) dx

oben r ( x)  x, f ( x) einsetzen.
 2   2 d
oben x( ), y( )   ( ) cos ,  ( ) sin   einsetzen
2
xA
Polarkoordinaten:
s 
B
A
B


A
Bemerkung:
Heuristische Herleitung: ds  dx 2  dy 2  dz 2 , mit dx  x (t )dt ,… folgt die Formel.
Beispiel:
Klotoide, nicht elementar ausdrückbar, gegeben durch x(t )   cosa2 u 2 du , y(t ) sin a2 u 2 du :
s AB  
t
0
0
cos t   sin  t    1dt T
T
2
a
2
0
Methode:
t
2
a
2
2
2
T
0
Volumenberechnung. Erste Grundidee: Es sei gegeben ein 3D-Körper. F(x) stelle den
Flächeninhalt der zur (y, z)-Ebene parallelen Schnittfiguren dar. Dann gilt: V   F ( x )dx
b
a
Wähle Schnittfl. so, dass sie möglichst einfach zu berechnen sind: Rechtecke, Kreissektoren…
Methode:

Oberflächenberechnung bei Rotationskörper (Ebene Fkt. r (t )  x(t ), y(t ) , Achse). Es gilt:
O  2  y (t ) x (t ) 2  y (t ) 2 dt
tB
tA
Herleitung  Kreiskegelstumpf (y(t), ds)  Kreisringsektor
Beispiel:
Herleitung für Lamberts flächentreues Kartenbild  Kugeloberfläche = Zylindermantelfläche!!
Methode:
Berechnung von Flächenmittelpunkt, Schwerpunkt. (Vgl. FB S46) Es gilt:
xs  G( x )dx   xG( x )dx , y s  H ( y )dy   yH ( y )dy , z s  J ( z )dz  ...
b
b
d
d
a
a
c
c
f
e
Dabei geben G(x), H(y), J(z) Kraftdichten an, die Ausdehnung in Richtung der jew. Achse.
Gemäss Mechanik ist S( xs, ys, zs) von der Wirklinie der homogen verteilten Kraft unabhängig.
11
Beispiel:
Ges: Schwerpunkt einer Halbkugel. Es gilt auf Grund Symmetrie ys = zs = 0.
Es gilt G( x )   ( R 2  x 2 )  Flächeninhalte der Schnittkreise, ρ = 1;   G( x )dx  V  23 R 3
R
0
x s  23 R 3   x ( R 2  x 2 )dx  
R
0
Definition:
   xs = …
R4
4
Trägheitsmoment. Diskret: i 1 mi d i 2 , im Kontinuum:  x    y 2 H ( y )dy ,  y    x 2G( x )dx .
n
b
d
a
c
Interpretation von G ( x ) als Masse m im Abstand x von der Achse. G(x) gibt die Ausdehnung
des betrachteten Bereichs in y-Richtung an. Allgemeiner: a    l 2 dV bez. einer Achse a.
B
Für die kinetische Energie bei einer Rotation gilt dann: Tx  12  x  2  12 mv 2  12 Vv 2 .
Flächenträgheitsmoment Jx, Jy des Bereichs B bez. der x- oder y-Achse für ρ = 1.
Polares Flächenträgheitsmoment J 0   ( x 2  y 2 )dF    2 dF , J0 = Jx +Jy
D
D
Merke dir die Herleitung des Trägheitsmoments des Zylinders seiner Achse!
Beispiel:
Flächenträgheitsmoment eines Kreises bez. y-Achse: J y  2 x 2 2 r 2  x 2 dx  4 r 4  J x
Methode:

Berechnung des Trägheitsmomentes eines Rotationskörpers ( r ( x)  x, f ( x) , x-Achse):
r
0
 x  12  ( f ( x )) 4 dx
b
a
Herleitung:  Trägheitsmomente infinitesimaler Zylinder
Beispiel:
Trägheitsmoment einer Vollkugel. Man nehme f ( x )  R 2  x 2 für x   R, R …
Definition:
Uneigentliches Integral 1. Gattung (f(a) existiert nicht, a ist Pol)

b
Uneigentliches Integral 2. Gattung (Integr.intervall unendlich):


Bemerkungen:
Es gilt:



f ( x )dx  
0


0
x 


0
a
 f ( x )dx
f ( x )dx  lim

 
b

  a
f ( x )dx
f ( x )dx   f ( x )dx . Notwendige, nicht jedoch hinreichende Bedingung
ist: lim f ( x )  0
Beispiel:
a
f ( x )dx  lim
1
dx  lim (log   log 1) existiert nicht!
 
x
12
Mehrdimensionale Differentialrechnung
Beispiel:
Eine Fkt. heisst linear, falls gilt: f ( x, y, z,...)  a1 x  a 2 y  a3 z  ...  c , (ai  R , nicht alle = 0).
Beispiel:
g : ( x, y )  g ( x, y )  1  ( x 2  y 2 ) beschreibt eine Halbkugelfläche. D(g): Einheitskreis.
Definition:
Eine Niveaulinie von f zum Niveau C ist gegeben durch die Gleichung f(x, y) = C.
Eine Niveaufläche von f zum Niveau C ist gegeben durch die Gleichung f(x, y, z) = C
Beispiel:
Definition:
Die Ebene 0 = ax + by + cz + d ist eine Niveaufläche der Fkt. f(x, y, z) = ax + by + cz + d.
Partielle Ableitung: . f ( x , y )  f ( x , y )  lim f ( x0  x, y0 )  ( x0 , y0 )
x
0
0
0
0
x 0
x
x
f x stellt die Steigung in jedem Punkt der Kurve f(x, y0) dar. Man leitet nach einer Variablen ab.
Beispiel:
4 f
( x, y, z,...)  f xxyz ( x, y, z,...)
xyzx
Definition:
Stetigkeit. Wenn für beliebige Folgen lim x n  x 0 , lim y n  y 0 , … gilt:
n
n 
lim f ( x n , y n ,...)  f ( x 0 , y 0 ,...) , so ist f(x, y,…) in ( x0 , y 0 ,...) stetig.
n 
Satz:
Satz von Schwarz. Sei f(x, y, z, …) eine Fkt. von mehreren Variablen. Setzt man Stetigkeit
in ( x0 , y0 , z 0 ,...) voraus, so gilt: f xy ( x0 , y 0 , z 0 ,...)  f yx ( x 0 , y 0 , z 0 ,...) , etc.  Reihenfolge egal!
Satz:
3D: Seien  ( x, y , z ) , ( x, y, z ) ,  ( x, y, z ) drei stetig diff’bare Funktionen mit einem achsenparallelen Quader als Definitionsbereich. Erst dann, wenn die Integrabilitätsbedingungen
 y ( x, y, z )  f xy ( x, y, z )  f yx ( x, y, z )   x ( x, y, z )
 z ( x, y, z )  f xz ( x, y, z )  f zx ( x, y, z )   x ( x, y, z )
 z ( x, y, z )  f yz ( x, y, z )  f zy ( x, y, z )   y ( x, y, z )
erfüllt werden, existiert eine Fkt. f(x, y, z) mit f x   ( x, y, z ) , f y   ( x, y, z ) , f z   ( x, y, z ) .
Bemerkung:
Auf folgenden Schritt achten: f x ( x, y, z )  2 x  f ( x, y )  x 2  v(y, z) !
13
Definition:
Die lineare Ersatzfunktion (Tangentialebene) von f im Punkte (x0, y0) ist diejenige lineare
Funktion, mit denselben partiellen Ableitungen in (x0, y0) und demselben Fkt.wert in (x0, y0).
Es gilt: z  f ( x0 , y 0 )  f x ( x0 , y 0 )( x  x0 )  f y ( x0 , y 0 )( y  y 0 )
Bemerkung:
Sei  ( x, y )  f ( x0  x, y 0  y )  ( f ( x0 , y 0 )  f x ( x0 , y 0 )x  f y ( x0 , y 0 )y ) , so gilt wieder:


 ( x, y )  o x 2  y 2 . Die Tangente konvergiert schneller gegen den Funktionswert, als
der Vektor ( x, y ) gegen (x0, y0) konvergiert.
Definition:
Als totales Differential bezeichnet man: df  f x ( x 0 , y 0 )dx  f y ( x 0 , y 0 )dy .
Die Abweichung f  f x ( x0  x, y0  y )  f ( x0 , y0 ) entspricht etwa df.
Satz:
Jede auf einer kompakten Menge A definierte stetige Funktion f : A  R hat ein globales
Maximum und ein globales Minimum.
Satz:
Potentielle Kandidaten für eine lokale Extremalstelle ( x0 , y0 ,...) für f ( x0 , y0 ,...) können sein:

Randpunkte des Definitionsbereiches

mindestens eine der partiellen Ableitungen in ( x0 , y0 ,...) existiert nicht

grad f ( x 0 , y 0 ,...)  0

Satz:
Verallgemeinerte Kettenregel. Sei F(t) = f( x(t) , y(t) , z(t),… ) eine zus’gesetzte Fkt. Es gilt:
dF
df
x(t ), y (t ), z(t ),...  f x x(t ), y (t ),...x (t )  f y x(t ), y (t ),... y (t )  ...  f ( r (t )  r
(t ) 
dt
dt
Definition:
Der Vektor grad f ( x0 , y 0 , z 0 ,...)   f x ( x0 , y 0 , z 0 ,...), f y , f z ,...  f ( x0 ,...) heisst Gradient.

r ist bekanntlich der Tangentialvektor.
Beispiel:
Bemerkung:


d
 f ( x(t ), y (t )  d  x(t )   1 x (t )  x2(t ) y (t )  x(t ) y (t ) 2 x(t ) y (t ) Quotientenregel
dt
dt  y (t )  y (t )
y (t )
y (t )
d
 f ( x(t ), y(t )  d x(t ) y(t )  y(t ) x (t )  x(t ) y (t )
dt
dt
Produktregel
d
 f ( x(t ), y(t )  d x(t ) y ( t )   y(t ) x(t ) y ( t )1 x  ln( x(t ))e y ( t ) ln( x ( t )) y (t )
dt
dt
Potenzregel
Achte auf den Unterschied zw. normaler und verallgemeinerter Kettenregel!  III.40.
14
Definition:


Richtungsableitung RA: De f ( x0 , y0 , z 0 )  e  grad f ( x0 , y0 , z0 ) ; e beliebiger Einheitsvektor.
Bemerkungen:
Die RA beschreibt die momentane Änderung des Funktionswertes an der Stelle ( x0 , y0 , z0 ) in

Richtung e . Die partiellen Ableitungen sind die RAen bezüglich der Koordinatenachsen.
Satz:
Die Richtung des Gradienten grad f ( x0 , y0 , z 0 ) gibt die Richtung der grössten RA von f in
( x0 , y0 , z0 ) an, also die Richtung, in der sich die Funktionswerte am extremsten ändern. Die
Länge des Gradienten ist gleich der grössten RA von f in (x, y, z).
Satz:
Der Gradient grad f ( x0 , y0 , z 0 ) von f in ( x0 , y0 , z0 ) steht senkrecht auf der Niveaufläche von f,
welche durch den Punkt ( x0 , y0 , z 0 ) geht.
Beispiel:
Die Tangentialebene im Punkt ( x0 , y0 , z0 ) auf die Niveaufläche ergibt sich mittels Gradienten:
f x ( x0 , y 0 , z 0 ) x  f y ( x0 , y 0 , z 0 ) y  f z ( x0 , y 0 , z 0 ) z  f x ( x0 , y 0 , z 0 ) x0  f y ( x0 , y 0 , z 0 ) y 0  f z ( x0 , y 0 , z 0 ) z 0
Bemerkung:
Koordinatentransformationen: FB S 81.
Satz:
Allgemeine Koordinatentransformation:
~
x ( u, v ) , y ( u, v )
 F (u, v )  F ( x(u, v ), y (u, v ))
u ( x, y ) , v ( x, y )
~
~
~
 F ( x, y )  F (u( x, y ), v( x, y ))  Fx  Fu  u x  Fv  v x , Fy  ...
Bei Ableitungen ist die allgemeine Kettenregel zu betrachten.
Definition:
~
Laplace-Operator ∆: f  f xx  f yy = f pp 
Beispiel:
Differentialgleichung eindimensionaler Wellengleichungen: f tt  c 2 f xx nach Koord’transfor-
1
p
~
fp 
1
p2
~
f  (Polarkordinaten)
~
~
~
mation ( f ( x, t )  f (u ( x, t ), v( x, t ))  f ( x  ct , x  ct )  verallg. Kettenregel!!): f uv  0 .
Lösungen: f (u, v )  F (u )  G ( v )  f ( x, t )  F ( x  ct )  G ( x  ct )
15
Mehrdimensionale Integralrechnung
Definition:
Geg. eine Fkt. f : ( x, y )  f ( x, y ) und ein im Def’bereich liegender Integrationsbereich B.

Bilde Teilbereiche ∆Bi

Wähle Zwischenpunkte (xi, yi) i = 1, 2, …, n. Feinheit mit Kreisscheibe definiert.

Riemann’sche Summe:

Riemann’sches Gebietsintegral:

n
i 1
f ( xi , yi )Fi

f ( x, y )dF  lim
B

n
i 1
f ( xi , yi )Fi . (Feinheit → 0)
Analog: Volumenintegral.
Bemerkung:
Volumenberechnung: mit F (x )  Flächeninhalt von Schnittfiguren
V   F ( x )dx
b
a
V   f ( x, y )dF
oder


 ( x)


 ( x)
V   f ( x, y )dF   F ( x )dx   dx 
B

 (x)
 ( x, y )

 ( x)
 ( x, y )
V   f ( x, y, z )dV   dx 
B
dy 
V   1dV
oder
B
B
f ( x, y )dy (Doppelintegral; von Reihenfolge unabh.)
f ( x, y, z )dz (Dreifachintegral, von Rf. unabh.)
Beispiel:
Die Masse eines Körpers wird allgemein beschrieben durch: M    ( x, y, z )dV
Beispiel:
J   e  x dx  J 2   e  x dx   e  y dy   dx  e  x  e  y dy   e   dF  
B

2



J   e  x dx  
2

Methode:

2

2





2
2
2
R R
Gauss’sche Glockenkurve.
Koordinatentransformation. Beispiel 2D.
Die Koordinaten (u, v) der uv-Ebene werden abgebildet in ( x(u, v) , y(u, v) ) der xy-Ebene.
Koordinatenlinien:


( x(u, v0 ), y(u, v0 ))  r (u, v0 ) , ( x(u0 , v ), y(u0 , v ))  r (u0 , v )
(i.A. krummlinig)
Koordinatenflächen: Analog, eine Koordinate wird festgehalten.
Flächeninhalt dF:
 xu
dF  ru (u, v )  rv (u, v )  du  dv  det 
 yu
Volumeninhalt dV:
 xu



dV  ru (u, v, w)  rv (u, v, w)  rw (u, v, w)  du  dv  dw  det  v u

wu
16
xv 
 du  dv
y v 
xv
vv
wv
xw 
v w   du  dv  dw

ww 
Definition:
Die lineare Abbildung der Koord’transformation wird in der Nähe des betrachteten Punktes
( x(u, v) , y(u, v) ) durch die Funktionalmatrix, Jacobimatrix approximiert:
 ( x, y )  x u

 (u, v )  y u
Bemerkung:
xv 
, analog 3D.
y v 
Die Funktionaldeterminante beschreibt die Volumen-/ bzw. Flächenverzerrung bei der
zugehörigen Abbildung. Aufmerksamkeit bei Punkten, die eine singuläre Abbildung ergeben!
Beispiele:
dF    d  d
Polarkoordinaten:
Zylinderkoordinaten: dV    d  d  dz
dV  r 2 sin   dr  d  d
Kugelkoordinaten:
Beispiel:
Polarkoordinaten: x  x(  , )   cos  , y  y (  , )   sin  . Die Punkte auf der φ-Achse
werden auf den Nullpunkt abgebildet ( Funktionalmatrix singulär)
Beispiel:
Ges: Volumen einer durch Mittelpunkt durchbohrten Kugel (RKugel = a, RBohrung = a/2)
Lös: V  2
B
2
a/2
0
0
V  2 d 
Beispiel:
a / 2
 a 2 / 4 x 2
a / 2
 a 2 / 4 x 2
a 2  x 2  y 2 dF  2
dx 
a 2  x 2  y 2 dy  Koord’transformation
 a 2   2 d  viel einfacher…
Ges: TM eines Zylinders (Achse z, Radius a, Höhe h) bez. eines Durchmessers im Grundkreis.

Z
2
a
h
0
0
0
( y 2  z 2 )dV   ( z 2   2 sin 2  )dV   d  d  dz   ( z 2   2 sin 2  )
Z
 1dV  
2

R
d  d  r 2 sin   dr  43 R3
Beispiel:
Volumen einer Kugel:
Satz:
Integrale mit Parameter. Gegeben sei eine stetige Fkt. von zwei Variablen f(t, x). Ferner sei
K
0
0
0
die partielle Ableitung fx ebenfalls stetig. Dann gilt:
Beispiel:
I)
b
d b
f (t , x )dt   f x (t , x )dt Beweis:  Differentialquotient.

a
dx a
II)
v( x )
d v( x )
f (t , x )dt  f ( v( x ), x )v' ( x )  f (u( x ), x )u' ( x )   f x (t , x )dt

u
(
x
)
u
( x)
dx
t x 1
0 ln t dt : ( x ) Integral nicht elementar lösbar  für ' ( x ) Satz I) anwenden:
1
ln t  t x
1
1
x 1 1
0 ln t dt  x  1[t ]0  x  1
1
17
Vektoranalysis
Definition:
Unter einem Skalarfeld versteht man eine reellwertige (also eindimensionale), auf einem
räumlichen Bereich B def. Funktion f : ( x, y, z,...)  f ( x, y, z,...) . Z.B. Temp., Potential…
Definition:
Ein Vektorfeld auf R n ist eine vektorwertige Funktion von n Variablen mit Definitionsbereich

B  R n . Durch ein Vektorfeld v ( x, y, z,...)  v1 ( x, y, z,...), v2 ( x...), v3 ( x...),... wird jedem Punkt

in B ein Vektor v ( x, y, z,...) zugeordnet. Z.B. Strömungs-, Kraft-, elektr. Felder.
Definition:
Ein Skalar- oder Vektorfeld heisst stationär,
wenn es zeitunabhängig ist.
instationär, wenn es zeitabhängig ist.  Dynamik
Definition:

Eine Feldlinie zu einem Vektorfeld v ( x, y, z ) ist eine Kurve, in der in jedem ihrer Punkte der
zu diesem Punkt gehörige Feldvektor tangential verläuft.
Definition:


Ein homogenes Vektorfeld ist von der Form v ( x, y, z )  a . Bsp. translatorisches Vektorfeld.
Beispiele:

e r ( x, y , z )
e


2
2
2 1/ 2
Coulomb’sches Feld: v ( x, y, z )   2 
  3  ( x, y , z ) . r  r  ( x  y  z )
r
r
r
Gravitationsfeld:
Magnetfeld:
Hagen-Poiseuille:
Definition:
Gradient:
Eigenschaften:

C'
 C'
v ( x, y , z )   3  ( x, y , z ) , v  2
r
r
 y


x
v ( x, y, z )  2 J  2
, 2
,0  ,
2
2
x y x y


v ( x, y, z )  0,0, (a 2  x 2  y 2 )
dabei ist J die Stromstärke.
Strömungsfeld
 f

f
f
grad f ( x, y, z )   ( x, y, z ), ( x, y, z ), ( x, y, z )   f
y
z
 x

Differentialoperator. Produziert aus einem Skalarfeld ein Vektorfeld.
grad f ( x, y, z ) steht senkrecht zur Niveaufläche von f, vgl. mit oben…
Bemerkungen:
Das Vektorfeld grad f ( x, y, z ) wird auch Gradientenfeld von f genannt.
Kennt man die Niveauflächen, so kennt man auch das Gradientenfeld u. u.
Definition:
Divergenz:
Eigenschaften:
v
v
v


div v ( x, y, z )  1 ( x, y, z )  2 ( x, y, z )  3 ( x, y, z )    v
x
y
z
Differentialoperator. Produziert aus einem Vektorfeld ein Skalarfeld
18
Satz:
Die Divergenz des Vektorfeldes ist vom gewählten (kartes.) Koordinatensystem unabh.:
v
v~
v1
v
v~
v~
( x, y, z )  2 ( x, y, z )  3 ( x, y, z )  1 ( , ,  )  2 ( , ,  )  3 ( , ,  )
x
y
z



Dies folgt mit Hilfe des Divergenzsatzes.
Satz:

Die Divergenz div v eines Vektorfeldes in P0  ( x0 , y0 , z 0 ) ist ein Mass für den aus der
Volumeneinheit um P0 heraustretenden Fluss des Vektorfeldes.


div v ( x0 , y0 , z 0 )  0 „Flüssigkeit wird erzeugt“. P0 ist eine Quelle von v


div v ( x0 , y0 , z 0 )  0 „Flüssigkeit verschwindet“. P0 ist eine Senke, negative Quelle von v


v heisst dann quellenfrei.
div v  0
Definition:
 v v v v v v 


rot v ( x, y, z )   3  2 , 1  3 , 2  1     v
z z x x y 
 y
Rotation:
Eigenschaften:
Differentialoperator. Produziert aus einem Vektorfeld ein Vektorfeld.

rot v ( x, y, z )  0  Integrabilität.

rotv ist ein Mass für die Winkelgeschwindigkeit der Rotation.
Beispiel:


 
Für v ( x, y, z )  ω  r ergibt rot v ( x, y, z )  2 1 , 2 , 3   2 .
Satz:
Rotation von v ist vom gewählten (kartes.) Koordinatensystem unabh. (Satzes von Stokes)
Satz:
Satz:



rot v ( x0 , y 0 , z 0 ) gibt Richtung und Stärke der „Wirbelung“ des Vektorfeldes v in ( x0 , y0 , z0 ) an.

Das Vektorfeld weist in ( x0 , y0 , z0 ) einen Wirbel auf, der senkrecht zu rot v ( x0 , y 0 , z 0 ) verläuft.



rotv heisst deshalb Wirbelstärke von v . Gilt rot v ( x, y, z )  (0,0,0) , so heisst dieses wirbelfrei.
Differentialoperatoren lassen sich zus’setzen. Achtung, nicht jede Zus’setzung ist sinnvoll!
div grad f ( x, y, z ) = f xx  f yy  f zz  f
 Laplace-Operator. (SkalarF  SkalarF)
rot grad f ( x, y, z ) = 0,0,0
 Die Rotation eines Gradientenfeldes ist Null.
 Gradientenfelder sind wirbelfrei
 Das Resultat folgt aus dem Satz von Schwarz.
 GradientenF erfüllen Integrabilitätsbedingungen.

div rot v ( x, y, z ) = 0.
Satz:
Es gilt:
 Rotationsfelder sind quellenfrei.


rot rot v  grad div v  ( v1 , v2 , v3 )
19
 

div pv  v grad p p div v
Satz:
Flächen lassen sich wiedergeben, durch: (Analog in höheren Dimensionen)


Bemerkung:
Graph einer Fkt. von zwei Variablen f(x, y)

Parameter: r (u, v)  x(u, v), y(u, v), z(u, v)

eine Gleichung g(x, y, z) = 0
Die Parameterdarstellung ist eine Abbildung von der Parameterebene in den 3D-Raum.
Man definiert Parameterlinien ähnlich wie Koordinatenlinien. (ein Parameter festhalten)
Definition:


Für eine Tangentialebene zu einer Fläche S: r (u, v ) im Punkt r (u0 , v0 ) gilt:




r (u, v )  r (u0 , v0 )  uru (u0 , v0 )  vrv (u0 , v0 ) .
Alternativ: mit Hilfe des Gradienten, falls S durch g(x, y, z) = 0 gegeben ist.
Beispiel:

Die Tangentenfläche einer Kurve s (u )  ( x(u ), y (u ), z (u )) ist die Fläche, die beim
Durchlaufen der Kurve von der Tangente an die Kurve überstrichen wird:



r (u, v)  s (u)  vt (u)
Definition:
Satz:


Für den Normaleneinheitsvektor n zur Fläche S: r (u, v ) in P (u0 , v0 ) gilt:



ru (u0 , v0 )  rv (u0 , v0 ) 

. ( ru (u0 , v0 ) , rv (u0 , v0 ) Rchtg. der Tang. an Parameterlinien)
n (u 0 , v 0 )   

ru (u0 , v0 )  rv (u0 , v0 )
Für den Oberflächeninhalt O eines durch Parameterdarstellung gegebenes Flächenstück



S: r (u, v ) (u, v  B) gilt: O   ru (u, v )  rv (u, v ) du  dv
B
Heurist.: betrachte dO des von benachbarten Parameterlinien aufgeschlagenen infinit. Vierecks.
Für den Oberflächeninhalt O eines durch explizite Darstellung gegebenes Flächenstück

S: f(x, y) (x, y  B) gilt: zunächst ist r (u, v, f (u, v )) , dann folgt aus oben
O  
B
Beispiel:
Definition:
( f x ( x, y )) 2  ( f y ( x, y )) 2  1  dx  dy
2


Kugeloberfl.: S: r (u, v )  ( R sin v cos u, R sin v sin u, R cos v )  O   du  R 2 sin vdv  4R 2
0
0



Es sei v ( x, y, z ) ein Vektorfeld, im Bereich D( v ) definiert. Sei S ein vollständig in D( v )

liegendes, mit einer ausgezeichneten Normalenrichtung n versehenes und in
Parameterdarstellung gegebenes Flächenstück. Dann versteht man unter dem Fluss Φ:
 
   v  n dO
S
20

Φ ist eine Grösse für die „Menge“ eines Volumens, die pro Zeiteinheit in Richtung n durch
das Flächenstück S hindurchfliesst, also ein Volumen pro Zeiteinheit. Es gilt wegen oben auch:



    v x(u, v ), y(u, v ), z (u, v )  ru (u, v )  rv (u, v ) du  dv , B = Parameterber. in der uv-Ebene
B
Methode:
Mit Parameter: Der Normalenvektor muss nicht normiert werden!
Vorgehen:

 gegebene Oberfläche darstellen mit Parameter  r ( x(u, v ), y (u, v ), z (u, v ))

 gegebenes Vektorfeld auf Oberfläche darstellen  r von oben einsetzen

 Normalenvektor n (u, v ) mit ausgezeichneter Richtung angeben
 Skalarprodukt
Beispiel:
 Integration
Ges.: Fluss des zu einer geg. Ladung e gehörenden Coulombfeldes durch eine Kugeloberfläche.

e
e 
e  
v  C  3 r     C  3 r  n dO  Kugeloberfläche!    C 3 R  dO  4Ce
S
S
R
r
r
Satz:

Es sei v ( x, y, z ) ein Vektorfeld und B ein endlicher räumlicher Bereich mit berandender Fläche

B . Auf B sei der äussere Normaleneinheitsvektor ausgezeichnet. v sei in ganz B einmal
 

stetig diff’bar. So dann gilt der Divergenzsatz, Satz von Gauss:    v  n dO   div v dV
B
Definition:
B


Sei v ( x, y, z ) ein stetig diff’bares Kraftfeld (Vektorfeld!) im Bereich D( v ) definiert. Sei W ein

vollständig in D( v ) verlaufender Weg mit Ausgangspunkt P und Endpunkt Q. (Weg = eine mit

Durchlaufsinn versehene Kurve.) Unter der Arbeit, die v entlang dem Weg W verrichtet,
 
versteht man folgenden Sachverhalt: A   v  dr
W
tQ 


Falls W in Parametern geg.: r (t )  x(t ), y(t ), z(t ) r (t P )  r (t Q ) : A  t v ( x(t ), y (t ), z (t ))  dr dt
P
Beispiel:
Für elektr. Felder heisst die Arbeit elektrische Spannung, in der Strömungslehre Zirkulation.
Satz:
Es gilt:
 
 
A   v  dr  A    v  dr ,
Methode:
Vorgehen:
 Weg parametrisiert festlegen
W
 
 
 
A   v  dr   v  dr   v  dr
W1 W2
W
W1
W2
 Vektorfeld entlang Weg in denselben Parametern beschreiben (einsetzen!)
 Skalarprodukt
Satz:
 Integrieren

Es sei v ( x, y, z ) ein reguläres, d.h. stetig differenzierbares Vektorfeld, im gesamten Bereich



D( v ) definiert (wichtig!). Sei S ein vollständig in D( v ) enthaltenes, mit n orientiertes
21

Flächenstück mit Rand S  Richtung  C . Dabei müssen n und die Laufrichtung ein
Rechtssystem bilden. Es gilt der Satz von Stokes:
Methode:
Beispiel:
Definition:
Vorgehen:


 
 v  dr   rot v  n dO
C
S
 Flächenstück S zweifach parametrisiert festlegen.

 n bestimmen (Normierung kürzt sich mit dem im dO enthaltenen Faktor)

 rotv berechnen (auf S)
 Skalarprodukt, Integrieren.


Sei v ( x, y, z ) ein reguläres Vektorfeld mit rot v  (0,0,0) und sei C ein Weg, der den Rand

eines ganz in D( v ) liegenden orientierten Flächenstücks S bildet  Arbeit längs C gleich Null.



Ein Vektorfeld v ( x, y, z ) heisst konservativ, wenn für alle P, Q  D( v ) , dass die Arbeit von v
längs allen Wegen von P nach Q gleich gross ist
Satz:
Definition:
Satz:
Satz:

Ein Vektorfeld v ist genau dann konservativ, wenn für alle geschlossenen Wege W die Arbeit

von v längs W verschwindet.


Lasse sich v ( x, y, z ) als Gradientenfeld v  grad f einer Funktion f ( x, y, z ) schreiben. So

wird f ( x, y, z ) Potential, v ( x, y, z ) das zugehörige Potentialfeld genannt.

Genau dann ist das Vektorfeld v konservativ, wenn es ein Potentialfeld ist, d.h. wenn es eine

Skalarfunktion f ( x, y, z ) gibt mit v  grad f .



Ist v ein Gradientenfeld v  grad f , so ist die Arbeit des Vektorfeldes v längs eines von P
nach Q führenden Weges gerade gleich der Potentialdifferenz f ( xQ , yQ , z Q )  f ( x P , y P , z P ) .
Bemerkungen:
Satz:
Satz:

Das Potential f eines Potentialfeldes v ist bis auf eine additive Konstante eindeutig bestimmt.

Die Niveauflächen von f heissen Potentialflächen. v  grad f steht dazu immer senkrecht.



Ist v ein Potentialfeld, so ist v zwingend wirbelfrei, d.h. es gilt rot v  (0,0,0) .



(Umkehrung +). Es sei v ein Vektorfeld mit rot v  (0,0,0) , dessen Def’bereich D( v ) einfach

zusammenhängend ist. Dann ist v ein Potentialfeld. (ein Bereich D heisst einfach zus’-
hängend, wenn sich jeder geschlossene Weg W in D stetig auf einen Punkt zus’ziehen lässt)
22
Satz:

Integrabilitätsbedingungen. Zu einem Vektorfeld v  ( , ,  ) sei das Potential gesucht,

dabei muss gelten: grad f  v  ( , ,  ) . Gemäss oben gilt: Ist der (gemeinsame)

Definitionsbereich D von  , ,  einfach zusammenhängend und ist v wirbelfrei, so existiert
eine Funktion f:

rot v  rot ( , ,  )  (0,0,0)  Integrabilitätsbedingungen.
Differentialgleichungen
Definition:
Eine gewöhnliche DG für die Funktion y : x  y ( x ) hat die Form F ( x, y, y' , y' ' ,..., y ( n ) )  0
n bezeichnet man als Ordnung der DG. Bei mehren Variablen, heissen die DGs partiell.
Beispiel:
Wachstumsvorgänge:
  a  m mit allg. Lösung m(t )  m0 e at
m
Abklingvorgänge:
y   k  y mit allg. Lösung y (t )  y 0 e  kt  Halbwertszeit: 
ln 2
k
Definition:
Eine DG 1. Ord. y '  f ( x, y ) ordnet jedem Punkt (x, y) eine Steigung zu  Richtungsfeld.
Satz:
Eindeutigkeitssatz. Es sei f ( x, y ) in D(f) stetig und nach y stetig partiell diff’bar. Dann gibt es
durch jeden Punkt x0 , y 0  im Inneren von D(f) genau 1 Lösungskurve für die DG y '  f ( x, y ) .
Bemerkung:
Beispiel:
Definition:
Überprüfe Differenzierbarkeit nach y insbesondere bei nichtlinearen DGs.
v ( x, y ( x ))

Sei v ( x, y ) ein gegebenes Vektorfeld. Es gilt: y '  2
. Nach obigem Satz findet man
v1 ( x, y ( x ))
eine eindeutige Lösung y(x) zu x0 , y 0  , wenn die Diff’barkeitsbedingung rechts erfüllt werden.
Die Menge aller Lösungen einer DG y '  f ( x, y ) heisst deren allgemeine Lösung. Sie
entspricht einer Schar von Kurven, der so genannten einparametrigen regulären
Kurvenschar.
Beispiel:
Ges.: DG 1. Ordnung zu einer gegebenen einparametrige reguläre Kurvenschar f(x, y(x), C) = 0
Vorgehen: Scharparameter C eliminieren aus f und f’.
Satz:
Kann die DG die Form h( y ) y '  g ( x ) annehmen, so heisst sie separierbar.
Methode:
Sei f ( x, y ) einer DG y '  f ( x, y ) von der linearen Form g (u ) mit u  ax  by ( x )  c .
Substituiert man u, so erhält man eine separierbare DG für u(x).
23
Beispiel:
y’ = (2x +3y)2  u(x) = 2x +3 y  y = ⅓ (u(x) – 2x)  y‘ = ...  y eliminiert, DG separierbar.
Methode:
Sei f ( x, y ) einer DG y '  f ( x, y ) von der Form g (u ) mit u  y / x . Substituiert man u, so erhält
man eine separierbare DG für u(x).
Definition:
Eine DG 1. Ordnung heisst linear, wenn sie von der Form y '  p( x ) y  q( x ) ist. Die rechte
Seite ist also eine lineare Funktion in y. p(x), q(x) sind beliebig. q(x) heisst inhomogenes Glied
oder Störglied. Gilt q(x) = 0, so heisst die DG y '  p( x ) y homogen, sonst inhomogen.
Satz:
Homogene lineare DGs sind separierbar.
Satz:
Man erhält die allg. Lösung der DG y '  p( x ) y  q( x ) , indem man eine partikuläre Lösung
y 0 ( x ) und zu ihr die allgemeine Lösung der zugehörigen homogenen DG y '  p( x ) y addiert.
Bemerkung:
Sind y 0 ( x ) und y1 ( x ) zwei partikuläre Lösungen von y '  p( x ) y  q( x ) , so ist ihre Differenz
y1 ( x ) - y 0 ( x ) eine Lösung der homogenen DG, wie man durch Einsetzen verifizieren kann.
Methode:
Verfahren von Lagrange. Gegeben: eine lineare DG 1. Ordnung y '  p( x ) y  q( x )
 homogene Lösung y h  0 bestimmen, es gilt y' h ( x )  p( x ) y h ( x ) .
 Ansatz von Lagrange, Variation der Konstanten für part. Lösung: y0 ( x )   ( x ) y h ( x )
 y0 ( x ) in DG einsetzen, vereinfachen
  (x ) bestimmen, dabei auf Integrationskonstante verzichten (part. Lösung…)
 Allgemeine Lösung:
Beispiel:
homogene + partikuläre Lösung
g x ( x, y )
, g y ( x, y )  0 .
g y ( x, y )
Ges: Eine Fkt. g ( x, y ) , deren Niveaulinien  ( x, y )   ( x, y ) y '  0 erfüllen.  Integrabilität…
Ges: DG der Niveaulinien g ( x, y )  C  totales Differential: y'  
DGs  ( x, y )   ( x, y ) y '  0 , die  y ( x, y )   x ( x, y ) erfüllen, heissen exakte DGs.
Definition:
Sei g ( x, y ) ein ebenes Potential. Ein Vektor von dessen Gradientenfeld steht immer senkrecht
auf der entsprechenden Niveaulinie von g ( x, y ) . Die Feldlinien des Gradientenfeldes bilden die
Orthogonaltrajektorien zur Schar der Niveaulinien.
24
Methode:
Jede Schar von Kurven ist Lösung einer DG der Form y’ = f ( x, y).  Parameter C eliminieren.
Die Orthogonaltrajektorien müssen dann folgender DG erfüllen: y '  
Beispiel:
1
.
f ( x, y )
Geg: Kurvenschar y = C x2. Ges: Orthogonaltrajektorien.  C eliminieren  DG der
Kurvenschar: y’ = 2y/x = f (x, y)  DG der Orthogonaltrajektorien: y’ = - x/(2y)
Definition:
Eine Enveloppe zu einer Kurvenschar F ( x, y, C )  0 findet man nach Elimination des
F ( x, y , C )  0
Scharparameter C aus folgendem Gls:
FC ( x, y, C )  0
Satz:
Eindeutigkeitssatz. Geg: y ( n )  f ( x, y, y' ,..., y ( n 1) ) . f sei in x stetig und nach y, y’,…, y(n-1)
stetig partiell diff’bar. Dann gibt es zu vorgegebenen Randwerten eine eindeutig bestimmte
Fkt. y(x), die Lösung der DG ist und die RB y( x0 )  y0 ( 0) , y' ( x0 )  y0 (1) , y ( n1) ( x0 )  y0 ( n1)
erfüllen. Die allg. Lösung einer DG n-ter Ordnung ist eine reguläre n-parametrige
Kurvenschar.
Bemerkung:
Komplizierte DGs mit Hilfe von linearen Ersatzfkt., also Approximationen, vereinfachen.
Definition:
Eine DG n. Ordnung heisst linear, wenn sie von der Form y ( n )  pn 1 ( x ) y ( n 1)  ...  p0 ( x ) y  q( x )
ist. pi(x), q(x) sind beliebig. q(x) heisst inhomogenes Glied oder Störglied. Gilt q(x) = 0, so
heisst die DG y '  p( x ) y homogen, sonst inhomogen.
Satz:
Für eine homogene lin. DG ist jede Linearkombination von Lösungen wiederum eine Lösung:
y h ( x )  C1 y1 ( x )  C2 y 2 ( x )  ...  Cn y n ( x ) . Die Ci yi (x ) sind dabei linear unabhängig!
Satz:
Man erhält die allg. Lösung der linearen DG n. Ordnung, indem man eine partikuläre Lösung
y 0 ( x ) und zu ihr die allgemeine Lösung der zugehörigen homogenen DG addiert.
Methode:
Verfahren von Lagrange. Gegeben: eine lineare DG 2. Ordnung y' ' p1 ( x ) y' p0 ( x ) y  q( x ) .
 homogene Lösung y h  0 bestimmen, es gilt y h ( x )  C1 y1 ( x )  C2 y 2 ( x ) .
 Variation der Konstanten für part. Lösung: y0 ( x )   1 ( x ) y1 ( x )   2 ( x ) y 2 ( x )
 Es gilt zusätzliche Annahme:  '1 ( x) y1 ( x)   ' 2 ( x) y2 ( x)  0
 y0 ( x ) in DG einsetzen, vereinfachen. Mit Ann. ergibt sich ein Gls.; nach  i ( x ) auflösen.
  i ( x ) bestimmen, dabei auf Integrationskonstante verzichten (part. Lösung…)
 Allgemeine Lösung
homogene + partikuläre Lösung
25
Definition:
Eine DG der Form y ( n )  a n1 y ( n1)  ...  a 0 y  0 mit a0 , a1 ,.., an1  R heisst (homogene)
lineare DG mit konstanten Koeffizienten.
Methode:
Zur Lösung einer lineare DG mit konstanten Koeffizienten: Der Ansatz y ( x )  e x führt zum
so genannten charakteristischen Polynom:  n  a n1 n1  ...  a1  a 0  0 .
Satz:
Für mehrfache und komplexe Nullstellen des chP einer linearen DGmkK gilt zusätzlich:
Sei α k-fache NST des chP. k linear unabhängige Lösungen sind dann:
y ( x )  ex , y ( x)  xex , … , y ( x )  x k 1ex
Sei   a  ib ,   a  ib , b  0 , ein Paar konjugiert komplexer k-facher NST des chP. Man
findet dann 2k linear unabhängige Lösungen der DGmkK:
y( x)  eax cos bx  y ( x )  eax sin bx
…
y( x)  xeax cos bx  y ( x )  xeax sin bx
y( x)  x k 1eax cos bx  y( x)  x k 1eax sin bx
Bemerkung:
1
2
( y1 ( x )  y 2 ( x ))  e ax cos bx und
1
2i
( y1 ( x )  y 2 ( x ))  e ax sin bx
Beispiel:
y ( 4)  2 y' ' y  0   4  2 2  1  0  y( x)  C1 cos x  C2 x cos x  C3 sin x  C4 x sin x
Definition:
Eine Eulersche DG n-ter Ordnung lässt sich in folgende Form bringen:
a
a
a
y ( n )  n1 y ( n1)  n22 y ( n 2 )  ...  0n y  0 , mit a0 , a1 ,.., an1  R
x
x
x
Methode:
Der Ansatz y ( x )  x  führt zum so genannten Indexpolynom:
 (  1)(  n  1)  an1 (  1)(  n  2)    a0  0 .
Satz:
Für mehrfache und komplexe Nullstellen des chP einer Eulerschen DGmkK zusätzlich:
Sei α k-fache NST des Indexpolynoms. k linear unabhängige Lösungen sind dann:
y ( x )  x , y( x)  (log x) x , … , y ( x )  (log x)k 1 x
Sei   a  ib ,   a  ib , b  0 , ein Paar konjugiert komplexer k-facher NST des
Indexpolynoms. Man findet dann 2k linear unabhängige Lösungen der DGmkK:
y( x)  xa cos( b log x)

y( x )  xa sin( b log x )
y( x)  (log x) xa cos( b log x)

y( x)  (log x) xa sin( b log x)
…
y( x)  (log x)k1 xa cos( b log x) 
y( x)  (log x)k1 xa sin( b log x)
26
Definition:
Die inhomogene lineare DG 2.Ordnung mit konstanten Koeffizienten x  2x   2 x  s(t )
beschreibt Schwingungsprobleme. Z.B. gedämpfte Federschwingung, elektr. Schaltkreise…
Beispiel:
Homogen:
Partikulär:
x  2x   2 x  0 . Das chP führt zu 1, 2    2   2

    starke Dämpfung
x h (t )  C1e 1t  C 2 e  2t

    kritische Dämpfung
x h (t )  C1e  t  C 2 te  t

    schwache Dämpfung
xh (t )  e  t (C1 cos( * t )  C 2 sin(  * t ))
1 , 2  0 !
*   2  2
x  2x   2 x  P cos(t )  Ansatz (stationäre Lösung!!): x0 (t )  A cos(t   )
P2
2
2
führt zu: tan   2
und A  2 2
4  ( 2   2 ) 2
  2
2
Horizontale Tangente von A2 ( ) in  1  0 und  2   2  22 .

    Starke Dämpfung und kritische Dämpfung.  eine hor. Tangente

    Schwache Dämpfung
o
o
1
2
   
0 
1
2

 Eine hor. Tangente. A2 ( ) monoton fallend…
 Zwei hor. Tangenten.   2 heisst Resonanzfrequenz.
für   0 hat A2 ( ) eine Polstelle  Resonanzkatastrophe!
Allgemein:
Definition:
x h (t )  x0 (t )  x (t )
Ein System von DGs 1. Ordnung für Fkt. y1 ( x) , y2 ( x) hat folgende Form:
y1 ' ( x )  f 1 ( x, y1 , y 2 )
.
y 2 ' ( x )  f 2 ( x, y1 , y 2 )
Eine Lösung des Systems ist ein Paar von Funktionen
y1 ( x) , y2 ( x) . Der Eindeutigkeitssatz gilt.
y1 ' ( x ) 
y2
y 2 ' ( x )  F ( x, y1 , y 2 )
Beispiel:
Für y ' '  F ( x, y, y ' ) findet man
Definition:
ein DGSystem heisst autonom, falls die Grundvariable x (oder t, etc) nicht explizit auftritt.
Beispiel:
Für x  2x   2 x  0 findet man
Definition:
Geg: Autonomes DGS x ( x )  f1 ( x, y )
x 
v
, da t nicht explizit vorkommt: autonom!
v   2v   2 x
T

y ( x )  f 2 ( x, y ) . Sei v ( f1 ( x, y), f 2 ( x, y)) ein VektorF.

Dann bilden die Lösungen x (t ) , y (t ) nach Definition Feldlinien von v eine mit Randpunkten
t0, x0(t0), y0(t0) fixierte und mit richtigem Durchlaufssinn versehene Feldlinie heisst
Trajektorie, die Schar der Trajektorien nennt man das Phasenporträt des Systems.
27
f ( x, y )
y
 2
x
f 1 ( x, y )
Bemerkung:
Man nütze folgende Eigenschaft aus für die Feldlinien y(x): y ' 
Definition:
Lineare autonome DGSysteme 1. Ordnung mit konstanten Koeffizienten haben folgende Form:
x1  a11 x1  a12 x2  b1

 
, auch schreibbar als: x  Ax  b
x 2  a 21 x1  a 22 x2  b2
Methoden:

Lösungsmethode mit Hilfe der Linearen Algebra: (homogener Fall, b  0 )
 A auf Diagonalform bringen  Eigenwertmatrix und Eigenvektoren.
 Betrachte System bezüglich der Eigenbasis, es ist nun „entkoppelt“ und einfach zu lösen.
 Zurück zu den ursprünglichen Funktionen…

Lösungsmethode mit Hilfe der Elimination: (homogener Fall, b  0 )

aus dem DGSystem eine unbekannte Funktion eliminieren (z.B. x2)

Man erhält eine lineare DG 2. Ordnung mit konstanten Koeff.  chP …
Bemerkung:
Das oben erwähnte chP stellt zugleich das chP von A dar!
Satz:


Stabilitätsverhalten von x  Ax . Ggw. in (0, 0). Seien α1, α2 die Eigenwerte der Matrix A.

1   2  0  x1  C1e t  C2e t , x2  ...

1  0   2
 x1  C1e1t  C2e 2t , x2  ...
 Ggw. instabil, (0,0) gemieden.

0  1   2
 x1  C1e1t  C2e 2t , x2  ...
 Ggw. instabil, (0,0) Ausgangsp.

1 , 2 seien konjugiert komplex
1
o 1  ib ,  2  ib (ri)
2
 Ggw asymptotisch stabil.
(ri = rein imaginär, pR = mit pos. Realteil, nR = …)
 x1  C1 cos(bt )  C2 sin( bt )
 Ggw stabil , Traj. period.
o 1  a  ib ,  2 …(pR)  x1  e at (C1 cos( bt )  C2 sin( bt ))  Ggw instabil, Strudelp.
o 1  a  ib ,  2 …(nR)  x1  e at (C1 cos( bt )  C2 sin( bt ))  Ggw asympt. stabil.
28
Potenzreihen
Definition:
Partialsumme ist eine Teilsumme einer Reihe. Konvergent heisst eine Reihe, falls sie sich
schreiben lässt als:


k 0
ak  s , sonst divergent.
Beispiel:
1
 1  x 2  x 4  x 6  ... für x  1 (folgt aus Summenformel für geometrische Reihen…)
2
1 x
Satz:
Konvergiert eine Reihe, so gilt lim k  a k  0 . Umkehrung gilt aber nicht (vgl. harmonische R).
Satz:
Alterniert eine Reihe und gilt lim k  a k  0 und an  an1 , so konvergiert die Reihe.
Definition:
Potenzreihe:


k 0
a k x k  a0  a1 x  a 2 x 2  ... . Konvergenzbereich heisst die Menge der x-
Werte, für die die Potenzreihe konvergiert.
Satz:
Der Konvergenzbereich einer Potenzreihe ist ein offenes, halboffenes oder abgeschlossenes
Intervall mit 0 als Mittelpunkt.
Bemerkungen:
Eine Potenzreihe definiert im Konvergenzbereich (KB, KI) eine Fkt., deren Werte sich mit
beliebiger Genauigkeit numerisch bestimmen lassen.
Am Rand lässt sich keine Aussage machen über das Verhalten: Konvergenz oder Divergenz.
Betrachtet man komplexe Potenzreihen, so ergibt sich in der Gauss’schen Zahlenebene ein
Konvergenzkreis mit Mittelpunkt z0 als KB. Konvergenzbereichs in R : Konvergenzradius.
Mittelpunkt des KB muss nicht zwingend 0 sein:  Koordinatenverschiebung x = t – t0
Satz:
Im Innern des Konvergenzintervalls darf man mit Potenzreihen wie mit Polynomen rechnen.
Man darf gliedweise addieren, subtrahieren, multiplizieren, differenzieren und integrieren.
29
Beispiel:
x
1
x2 x3
dt   (1  t  t 2  ...)dt  x 

 ... im KI x  1 .
0 1 t
0
2
3
log( 1  x )  
Rand:
x
x = -1:
 harmonische Reihe
 Divergenz.
x = 1:
 alternierendharmonische Reihe
 Konvergenz.
x
1
x3 x5
2
4
dt

(
1

t

t

...)
dt

x


 ... im KI x  1 .
0
0 1 t2
3
5
arctan x  
Beispiel:
x
Man bestimme eine Potenzreihe mit Mittelpunkt x0 = 1 für die Funktion:
1
1
1
1
1 1
1

 
  2 ( x  1)  3 ( x  1) 2  ... (KI = (-2, 4)
x 1
x  2 3  ( x  1) 3 1  3
3 3
3
Methode:
Allgemeiner: Polynomansatz: P( x )  a 0  a1 ( x  x0 )  ...  a n ( x  x0 ) n .
Aus der n-ten Ableitung aufwärts: a0  P( x0 ) , a1  P' ( x0 ) a 2  12 P' ' ( x0 ) a n  n1! P ( n ) ( x0 )
Bemerkung:
Die lineare Ersatzfunktion folgt aus diesem Ansatz als Polynom 1. Ordnung!
Achtung: x0 beide Male einsetzen!!!
Definition:
Aus obigem folgt das Taylorpolynom (Ersatzpolynom) n-ten Grades von f in x0:
f ' ( x0 )
f ' ' ( x0 )
f ( n ) ( x0 )
Pn ( x )  f ( x0 ) 
( x  x0 ) 
( x  x0 ) 2  ... 
( x  x0 )n
1!
2!
n!
Dieses kann als Partialsumme der Taylorreihe angesehen werden.
Bemerkung:
Die Taylorreihe entspricht einer Potenzreihe.  KB offen, ... , Mittelpunkt x0  Für viele
Funktionen konvergiert die Taylorreihe in einer echten Umgebung von x0.
Beispiel:
Taylorpolynom Pn in x0 = 0 für f’(x) = ex:
Pn ( x )  1  x 
1 2
1
x  ...  x n
2!
n!
Weitere Beispiele im FB S 48!!!.
Beispiel:
Es lässt sich mit Reihenentwicklungen cos x  i sin x  e ix zeigen. e ix  1  ix 
Methode:
Koeffizientenvergleich. Anhand eines Beispiels:
Aus cos x  tan x  sin x folgt
1
(ix ) 2  ...
2!
1 2 1 4
1 3 1 5


2
1  x  x  ... c 0  c1 x  c 2 x  ...  x  x  x  ...
2!
4!
3!
5!


Bilde auf der linken Seite eine sauber notierte Potenzreihe und vergleiche dann die Koeff.
30
Satz:
Die Taylorentwicklung um x0 einer ungeraden Fkt. enthält nur Terme mit ungeradem Index,
die einer geraden Fkt. enthält nur Terme mit geradem Index.
Bemerkungen:
Bei nicht elem. lösbaren Integralen ermöglicht die TE des Integranden ein Fortfahren:
Ellipt. Integral 1. oder 2. Art:
 /2

0
1  k 2 cos 2 t  dt , Gauss’sche Fehlerfkt. ( x ) 
2
x
e

t 2
0
dt
Auch DGs können mittels Ansätzen mit Potenzreihen gelöst werden.
Komplexe Zahlen
Definition:
komplexe Zahl: z = a + ib.
i: imaginäre Einheit. a = Realteil, b = Imaginärteil.
Satz:
Es gelten die fundamentalen Rechengesetze. Summen, Produkte.. Inverse 1/z bestimmbar.
Beispiel:
1
1
 8  i   (8  i )( 5  1) 
  (3  i ) 2  ( 4  3i )

 
4
2
 5  i   (5  i )( 5  i ) 
Definition:
Komplexe Zahlen werden auf der komplexen (Gauss’schen) Zahlenebene betrachtet.
Definition:
Mit Hilfe von Polarkoordinaten folgt: ρ = |z| heisst Absolutbetrag und φ Argument arg z von z.
Satz:
Es gilt: cos  i sin   e i  ze mit |z| = 1 und arg z = φ. Allg.: z  z e i (Polardarstellung)
Beispiel:
z  z'  z e i  z' e i  z (cos   i sin  )  z' (cos   i sin  )  z  z' e i (  )
Satz:
Bei Multiplikation werden Absolutbeträge multipliziert und die Argumente addiert.
Definition:
Die konjugierte komplexe Zahl z von z ist gegeben durch: z  a  ib , z  z e i
Satz:
Realteil: a 
Satz:
Siehe FB S13. Herauszuheben ist: z  z  z , z n   z  e i   z e in (de Moivre  trigo.)
Beispiel:
z   3  i 3  6e i mit   3 / 4  z 10  6 5 e15i 2  6 5 e 3i 2  6 5 i
Beispiel:
(Umkehrung:
2
2
Vgl. FB S13
1
1
1
1
( z  z ) , cos   (e i  e i ) Imaginärteil: b  ( z  z ) , sin   (e i  e i )
2
2
2i
2
2
n
n
n
z ): z n  e i  Ansatz z  e i  z n  e i  e in  n   mod 2
Die Lösungen zk bilden auf dem Einheitskreis ein n-Eck. Erste Ecke: z1  e i1  e i n
31
Definition:
Komplexwertige Funktion:  : R  C  : t   (t )  g (t )  ih (t )
 : C  C ,  : z   ( z)
Ableitung von 1.Art:
(1.Art).
(2.Art)
 ' (t )  g ' (t )  ih ' (t )
Beispiel:
e '  cos t  i sin t '   sin t  i cos t  ie
Beispiel:
f ( z )  ze i
Entspricht einer Rotation der komplexen Zahlenebene um α.
f ( z )  rz
Streckung der komplexen Zahlenebene um den Faktor r.
it
it
f ( z )  z 2  (a 2  b 2 )  i 2ab Nehme in der Zahlenebene von z Parallelen zu den Koordina
tenlinien und betrachte deren Form in der Zahlenebene von f(z).
Definition:
Komplexes Polynom p: p( z )  c0  c1 z  ...  cn z n mit ci  C (Koeffizienten) und Grad n.
Beispiel:
Bestimmen von NST: p( z )  c 0  z n  z n  c 0  n verschiedene NST.
Satz:
Fundamentalsatz der Algebra: Es sei p ein Polynom mit Grad p ≥ 1. Dann gibt es
(mindestens) eine NST von p.
Satz:
Es seien p und q Polynome mit Grad p = n und Grad q = m ≤ n. Dann gibt es Polynome r und s
mit p(z)= r(z) q(z)+ s(z) und Grad s < m.
Satz:
p( z )  c0  c1 z  ...  cn z n lässt sich schreiben als: p( z )  c n ( z  z1 )( z  z n ) . (Linearfaktoren)
Satz:
Ein Polynom p vom Grad n hat höchstens n NST. (höchstens  algebraische Vielfachheit).
Satz:
Ist z0 eine NST des reellen Polynoms p, so ist auch die konjugiert komplexe Zahl z 0 eine NST.
32
Nachtrag, Ergänzungen, Listen
Schwingungen:
Harmonische Schwingungen können zweiteilig oder einteilig äquivalent notieren werden:
zweiteilig:
s(t )  B cos( t )  C sin( t ) B, C  R oder
einteilig:
s(t )  A cos(t   ) A,  R
Gedämpfte Schwingung: s(t )  e  at cos(t   ) a  0 . Achtung: Wendestellen sind die
Berührungsstellen mit e-at und –e-at!
Integration:
Lösungsmethode mittels den Rationalisierungsformeln: (FB S54) Bei trigonometrischen
2 tan 
2 tan x / 2
2t
 x
 tan x  

Integranden, wähle Substitution: t  tan   ( tan 2  
)
2
2
1  tan 
1  tan x / 2 1  t 2
2
tan x
2t
1
1 t2
 cos(x) =
 sin(x) =
 dx = 2 2 dt  d ( 2 arctan t )


2
1  tan 2 x
Integration:
1 t2
1  tan 2 x
1 t
1 t
Bei hyperbolischen Fkt. hilft die Umschreibung auf (z.B.) sinh x 
1
2
e
x
 e  x  oft weiter.
Rationale Fkt.: Zerlegung in möglichst einfache Brüche. Oder Form für (tan x)’ = …
Bei Wurzeltermen die Substitution t2 = [Wurzelterm] in betracht ziehen!
Integration:
Integration:

e 1
dx  Substitution: t  e  1  2tdt  e dx  t  1 … ■ Analog bei
2
x
x
2
x
dx
5 x
xa
x 1 a 1
x2
x
2x
,
dx

dx

...
 x 1  x 1
 ( x 2  1) 2 dx   2 ( x 2  1) 2 dx  ... ■

DGs:
1
x
x 2  16dx   Substitution: x = 4sinh t … ■
Ansätze, Lösugen für DGs folgender Form:
y ' '
x
1
y '
y0
1 x
1 x
y ' '2 y ' y  sin( 3x )
 allgemeine Lösung:
y  C1 x  C2e x
 Part. Lösung, Ansatz:
y p  A cos( 3x )  B sin( 3x )
y ' '2 y ' y  sin( 3x )  cos( 9 x )  Part. Lösung, Ansatz:
lm   mg sin(  )
y p 2  y p  C cos( 9 x )  D cos( 9 x )
 schwierig  lineare Approximation.:
33
lm   mg
DGs:
Spezielle Lösungsverfahren.
DG: 2 x  y cos x  (1  sin x ) y '  0
(ein Beispiel)
Methode 1:
u(x) = 1 + sin x  DG: (uy)’ = -2x  uy = x2  y = …
Methode 2:
φ(x,y) = 2x + ycos x ψ(x,y) = 1 + sin x  φy = ψx  es existiert eine f(x,y)
mit fx = φ und fy = ψ. Niveaulinien von f(x,y) sind ges. Lösungen der DG.
Methode 3:
Logarithmus:
Methode Lagrange.
Merke: ln y   ln( x)  ln x 1   y  1 x
Komplexe Zahlen: Ges: Menge aller Punkte in der Gauss’schen Zahlenebene mit |f( z)| = 2
f ( z) 
z  2i
z 1
 | z  2i | 2 | z  1 |  | z  2i |2  4 | z  1 |2  ( z  2i )( z  2i )  4( z  1)( z  1)
 3zz  4( z  z )  2i ( z  z )  einsetzen: z = x + iy  … ■
Komplexe Zahlen: Beweise: ( z  z ) 2  ( z  z ) 2 | 2 z |2  4 zz  ( 2 Re z ) 2  ( 2 Im z ) 2  4 x 2  4 y 2 … ■
Komplexe Zahlen: Ges: Elementare Form von cos3φ. cos 3  Re( e 3i )  Re(( e i ) 3 ). ( x  iy ) 3 =… ■
Rotationsmatrix:
cos t  sin t 0
Rotation um z-Achse  R   sin t cos t 0


0
1
 0
Trigonometrie:
Man beweise: arcsin x  arccos x  2  man setze x = sin t = cos (π/2 – t)! ■
Vektoranalysis:
Gibt es ein Vektorfeld v (x, y, z) mit rot v = (x, y, z)?  Nein, denn (div rot v) muss 0 sein!
Fluss:
Ges: Fluss von v(x, y, z) = (2x, y2, z2 + 7) durch die Oberfläche S der Einheitskugel
 divvdV   (2  2 y  2z)dV   2dV 
B
Vergleichsfkt.:
B
B
Minimumformel: a falls b  a  1 (a  b | a  b |)
b falls a  b  2
8
3
■
Symmetrie!!!
Maximumformel: a falls a  b  1 (a  b  | a  b |)
b falls b  a  2
Hyperbolische Fkt.: Man suche die Inverse Funktion zu y  2 x  2  x  y  2 sinh( x ln 2)  x = … ■
Fehlerrechnung:
Ges: Auswirkung der Messfehler beim Kosinussatz: c2 (a, b, α) = a2 + b2 – 2ab cosα
dc (a , b, ) 
(a  b cos  )
(b  a cos  )
ab sin 
da 
db 
d ■
c
c
c
34
Hauptsatz:
…der Infinitesimalrechnung: Man berechne die partiellen Ableitungen der Funktion:
x
x
0
0
f ( x, y )   sin( yt 2 )dt  f x  sin yx 2 , f y   t 2 sin( yt 2 )dt (Ableitung nach Parameter…) ■
x
g ( x)   sin( xt 2 )dt
0
Hauptsatz:
Folgen:
x
 g ' ( x)  f x ( x, x)  f y ( x, x)  sin x 3   t 2 sin( xt 2 )dt ■
0
2a 1
1
1
d
d
I (a )   e x 
( F ( 2a )  F (a ))  2e 2a  e a
a
da
da
Fibonacci Folge,
rekursiv definiert: fn+2 = fn + fn+1, mit f0 = 1, f1 = 1 (explizit, siehe LinAlg)
1 5
f
Goldener Schnitt:   lim n1 f  lim an    1  1   
, da  > 0
n 
n


n
2
Folgen und Reihen: Ges: Sind die Zahlenfolgen konvergent? Sind sie monoton? Sind sie beschränkt?
a)
3n 4  5n 2  2
an 
 an konvergiert gegen 3/7, also beschränkt, nicht aber monoton! ■
7n 4  4n 3
b)
a1 = 0, a2 = 1, an = ½(an-2 + an-1). für n = 3, 4, …
Es gilt: an+2 - an+1 = -½ (an+1 - an) = … = (-½)n  an  a1  k 0 ak 2  a  k 0 ( 1 2) k
k 1
1
 geom. Reihe: sn = 1  ( 1 )  Folge beschränkt, nicht aber monoton! ■
2
n 2
Grenzwertrechnen:
35
n2
36