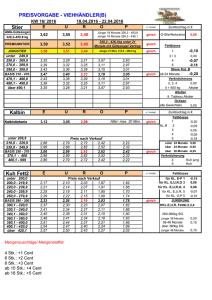
Musterbeispiel: Lineare Optimierung
Werbung

4 CK Preis- und Kostentheorie 14. Mai 2016 Funktionen Definition: Eine eindeutige Zuordnung zwischen den Elementen der Definitionsmenge D und einer Menge B (der Bildmenge) heißt Funktion. Die Elemente von D heißen Argumente, die Elemente von B Bilder oder Funktionswerte. Eindeutig heißt, dass jedem Argument genau ein (nicht mehr und nicht weniger) Bild zugeordnet wird. Definition: Eine Funktion f(x) = kx + d heißt linear. Eigenschaften: f(0) = d , d. h. der Funktionsgraph schneidet die Ordinate im Punkt (0/d). d heißt daher: Ordinatenabschnitt Die Funktion hat überall die konstante Steigung k = Error!. Von jedem Punkt aus ist der absolute Zuwachs gleich groß. Der Funktionsgraph ist eine Gerade. Anwendungen 1. Kosten, Erlös und Erfolg Kosten als Funktion der erzeugten Menge x (heißt auch Beschäftigungsgrad). K(x) = k x + F F....................... Fixkosten k ....................... variable Stückkosten x ....................... Menge (Beschäftigungsgrad) Beispiel: in GE (Geldeinheiten) in GE / ME (Geldeinheiten pro Mengeneinheiten in ME (Mengeneinheiten) Ein Betrieb hat eine Kapazität von 80.000 Stk pro Monat. Er hat Fixkosten von € 500.000,-- pro Monat. Die Erzeugung von 100 Stk. kostet den Betrieb jeweils € 3.000,--. Stellen Sie die Kostenfunktion als Gleichung dar. Verwenden Sie 1 GE = € 10.000 und 1 ME = 1.000 Stk. k kann als Error! = x [0 / 80.000] Error! = 30 €/Stk. berechnet werden. K(x) = 30 x + 50.000 mit Verwendet man die verlangte Skalierung dann ist: k = Error! = berechnet werden. K(x) = 3 x + 50 mit x [0 / 80] Error! = 3 GE/ME Darstellung als Funktionsgraph DERIVE: Eingabe des rechten Teils der Funktionsgleichung und dann im Grafikfenster plotten. EXCEL: in Spalte A die xWerte eintragen – in B die Formel =3*a2+50 eintragen und hinunterkopieren – Diagramm erstellen mit Diagrammtyp x-y! Wie hoch sind die Durchschnittskosten beim Beschäftigungsgrad 70 %? Seite 1 von 5 4 CK Preis- und Kostentheorie 14. Mai 2016 70 % BG heißt 0,7 · 80 ME = 56 ME K(56) = 3 · 56 + 50 = 218 GE, das sind € 2.180.000,-Stückkosten = Kosten pro Mengeneinheit = Error! = 3,89 GE/ME = 38,9 €/Stk. 30 € /Stk. sind variable Stückkosten, 8,9 €/Stk. ist der Fixkostenanteil. Je höher der Beschäftigungsgrad wird, desto kleiner wird der Fixkostenanteil. Durchschnittskosten oder Stückkosten Kd (x) = Error! = k + Error! Erlös als Funktion der erzeugten Menge x (heißt auch Beschäftigungsgrad). E(x) = p x E ...................... Erlös p ....................... Preis pro Mengeneinheit x ....................... verkaufte Menge in GE in GE / ME in ME Erfolg (Gewinn) als Funktion der erzeugten Menge x . G(x) = E(x) – K(x) Break-even-Punkt oder Gewinnschwelle: G(x) = 0 oder E(x) = K(x) Beispiel: Ein Betrieb hat eine lineare Kostenfunktion und eine Kapazität von 80 ME. Die Kosten bei 20 % BG sind 98 GE, steigt der BG um 50 Prozentpunkte dann erhöhen sich die Kosten um 122 %. Ermitteln Sie die Gleichung der Kostenfunktion, die variablen Stückkosten und die Fixkosten. Bei welchem BG liegt der BE, wenn der Verkaufspreis 5 GE/ME beträgt? Grafische Darstellung K(20 %) = K(16) = 98 = k · 16 + F K(70 %) = K(56) = 2,22 · 98 = 217,56 = k · 56 +F Elimination liefert k = 2,989 3 und F = 50,176 50 also K(x) = 3 x + 50 in [0 / 80] K(x) = E(x) 3x + 50 = 5x BG. x = 25 , das sind 31,25 % 2. Tarife Tarif als Funktion der verbrauchten Menge x T(x) = k x + G Seite 2 von 5 4 CK Preis- und Kostentheorie G ...................... Grundpreis k ....................... Tarif pro Verbrauchseinheit, Arbeitspreis x ....................... verbrauchte Menge Beispiel: 14. Mai 2016 in GE in GE / ME in ME Splittarif: Ein Energieversorgungsunternehmen macht folgende Angebote: Tarif A: Grundtarif ................... € 50,-- pro Monat Arbeitspreis 1 ............. € 0,15 pro kWh bis zu einem Monatsverbrauch von 500 kWh Arbeitspreis 2 ............. € 0,10 pro kWh für jede kWh über 500 kWh. Tarif B: Arbeitspeis ................. € 0,20 pro kWh und keine Grundgebühr Berechnen Sie die Gleichungen für beide Tarife. Stellen Sie die Tarife grafisch dar. Wann ist welcher Tarif für den Verbraucher günstiger? Wieviel kann man sich bei einem Verbrauch von 400 kWh, bzw. 1.000 kWh beim günstigeren Tarif ersparen? Tarif A: TA1(x) = 50 + 0,15x für x [0 / 500] TA2(x) = ax + b für x (500 / ) (linearer Ansatz, Parameter a und b, Buchstaben für die Parameter egal) man weiß: TA2(500) = TA1(x) = a · 500 + b = 50 + 0,15 · 500 500 a + b = 125 und TA2(600) = 125 + 0,1 · 100 = 135 = 600 a + b (der Wert 600 ist frei wählbar) Elimination liefert a = 0,1 (natürlich, das hätte man auch schon vorher wissen können) und b = 75 (das wäre die Grundgebühr für den zweiten Teil des Splittarifs, aber für den Verbrauch 0 kWh ist TA2 gar nicht definiert) daher: TA1(x) = 50 + 0,15x für x [0 / 500] und TA2(x) = 0,1x + 75 für x (500 / ) und TB(x) = 0,2x für x R+ Schneiden beider Tarife führt auf die Gleichungen: 50 + 0,15x = 0,2 x x = 1.000 irrelevant, weil 1000 nicht in [0 / 500] liegt. 75 + 0,1x = 0,2x x = 750 gültige Lösung weil 750 in (500 / ) liegt. ab einem Verbrauch von 750 kWh/Monat ist der Tarif A günstiger, vorher B. Seite 3 von 5 4 CK Preis- und Kostentheorie TA1(400) = 50 + 0,15 · 400 = 110 € TB(400) = 0,2 · 400 = 80 € 14. Mai 2016 Ersparnis 30 €/Monat TA2(1.000) = 75 + 0,10 · 1.000 = 175 € TB(1.000) = 0,2 · 1.000 = 200 € Ersparnis 25 €/Monat 3. Angebot und Nachfrage Angebotspreis als Funktion der Menge (supply) s(x) = a x + b Nachfragepreis als Funktion der Menge (demand) d(x) = c x + d spezielle Punkte: Sättigungsmenge SM Prohibitivpreis PP .. d(SM) = 0 d(0) = PP Gleichgewichtspreis = Preis, bei dem Angebotsmenge und Nachfragemenge gleich groß sind. s(x) = d(x) Elastizität der Nachfrage: Beispiel: (x) = – Error! = – Error! Bei einem Preis von € 70,-- pro Stück werden 250 Stück angeboten, aber 500 Stk. nachgefragt. Wird der Preis um 20 % gesenkt, dann sinkt das Angebot auf 180 Stk., die Nachfrage steigt jedoch um 28 %. Berechnen Sie die Angebots- und Nachfragefunktion! Angebot: s(250) = 70 = 250 a + b und s(180) = 56 = 180 a + b a = 0,2 und b = 20 also s(x) = 0,2x + 20 Nachfrage: d(500) = 70 = 500 c + d und d(640) = 56 = 640 c + d c = – 0,1 und d = 120 d(x) = 120 – 0,1x Wie hoch ist der Gleichgewichtspreis? 0,2x + 20 = 120 – 0,1 x 0,3 x = 100 x = 333,333 p(333,333) = 86,66 Wie hoch ist der Nachfrageüberhang bei einem Preis von 50 €/Stk.? 50 = 0,2xs + 20 xs = 150 Nachfrageüberhang 550 Stk. 50 = 120 – 0,1xd xd = 700 Wie hoch ist die Elastizität der Nachfrage bei einem Preis von 80 €/Stk.? d(x) = 80 = 120 – 0,1x x = 400 Stk. wird x um x = 40 erhöht, also um 10 %, dann muss der Preis auf d(440) = 120 – 0,1 · 440 = 76 gesenkt werden, das sind – 5 %. also = – Error! = 2 Seite 4 von 5 4 CK Preis- und Kostentheorie 14. Mai 2016 der Absatz ist also elastisch, weil bei einer Senkung des Preises um nur 5 % der Absatz doppelt so schnell (um 10 % ) steigt. Der Erlös wird bei einer Preissenkung also steigen! Grafik: 300 250 200 150 100 50 0 0 200 400 600 800 1000 1200 1400 Seite 5 von 5