Skript 2013

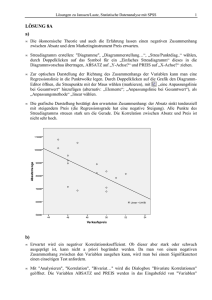
Skript Computergestützte Datenanalyse SS 12
(Anne Hagemann, SPSS)
Einordnung in den Forschungsprozess




Fragestellung
Untersuchungsplanung
Untersuchungsdurchführung
Vorbereitung der Datenanalyse
 Erstellung eines Kodierplans/Variablendefinition
 Dateneingabe
 Überprüfung der Dateneingabe/Datenscreening
 Umgang mit fehlenden Werten/Extremwerten
 Datenanalyse
 Berichterstellung
Grundlegendes zu SPSS
 Daten-Editor
 öffnet sich beim Start
 Datenansicht und Variablenansicht
 Datendateien werden als .sav-Dateien gespeichert
 SPSS Viewer
 Ausgabefenster
 enthält die Ergebnisse (Output) als Tabelle und Diagramme
 Ausgaben können als .spv-Dateien gespeichert werden
 Diagramm-Editor und Pivot-Tabellen-Editor
 zum Bearbeiten von Diagrammen und Tabellen im Output/Viewer
 Syntax-Editor
Tabellen in SPSS
 Tabellenformat das Standard in der SPSS-Ausgabe ist entspricht nicht akademischen
Anforderungen
 Rechtsklick auf Tabelle  Tabelle bearbeiten  in separatem Fenster
 Pivot  Zeilen und Spalten vertauschen
 Ändern der Tabellenform: Format  Tabellenvorlagen  Academic
 Schriftgröße, Ausrichtung, Dezimalstellen anpassen
 da Möglichkeiten der Bearbeitung begrenzt einfaches kopieren in Word/Excel, Screenshots
bei Powerpoint (Rechtsklick  Exportieren)
 benutzerdefinierte Tabellen
 Analysieren  Tabellen  Benutzerdefinierte Tabellen
 so können Statistiken etwa nach Geschlecht getrennt ausgegeben werden, ohne dass
Datei vorher geteilt werden muss
Diagramme in SPSS
 Zugriff über Diagramme  Diagrammerstellung oder Diagramme  Veraltete Dialogfelder
 durch Doppelklick auf Diagramm in der Ausgabe gelangt man in die Diagrammbearbeitung
 Kreisdiagramme
 Darstellung von kategorialen Merkmalen (z.B. Geschlecht, Haarfarbe…)
o Kreisdiagramm auswählen, Variable in „Feld aufteilen nach“ ziehen
 Balkendiagramme
 Darstellung des Mittelwerts einer Variablen für verschiedene Gruppen
o einfaches Balkendiagramm auswählen wenn Mittelwert nach einer Variable
getrennt gezeigt werden soll
o Variable auf die x-Achse, Mittelwert der berücksichtigt werden soll auf die yAchse
oder
o gruppiertes Balkendiagramm wenn Mittelwert nach zwei Variablen getrennt
gezeigt werden soll
o Variable auf die x-Achse, Mittelwertsvariable auf die y-Achse, dritte Variable
in „Clustervariable“ (z.B. Geschlecht)
oder
o gleiche Vorgehensweise bei Darstellung des Mittelwerts nach drei Variablen
getrennt
o dann unter Gruppen/Punkt-ID „Spaltenfeldvariable“ anklicken und Variable
in neu erscheinendes Feld ziehen
 Histogramm
 Darstellung von Häufigkeitsverteilungen (bei zu vielen Kategorien werden Kategorien
zusammengefasst)
o einfaches Histogramm wählen und Variable auf die x-Achse ziehen
o unter Elementeigenschaften „Normalverteilungskurve anzeigen“ wählen
 Boxplot
 Darstellung der Verteilung (Quartile) und Ausreißer einer Variablen
o einfachen Boxplot auswählen und Variable auch die x-Achse ziehen
 Streudiagramme
 Darstellung des Zusammenhangs zweier Variablen
 Identifizieren von bivariaten Ausreißern
o gruppiertes Streudiagramm auswählen und Variablen auf x- und y-Achse
ziehen
o evtl. Farbe der Punkte differenzieren nach weiterer Variable (z.B. Geschlecht)
Daten in SPSS einlesen
 …aus Textdatei (Editor)
 Vorteil bei Textdateien: Daten können problemlos in alle Programme eingelesen
werden
 Eingabe der Daten:
o Daten im „tab-delimited format“ eingeben (Tabs als Trennung zwischen den
Variablen)
o jede Zeile = ein Fall/Untersuchungsteilnehmer
o erst Zeile =Variablennamen
o Vorteil der Tabs als Trennzeichen: kommen in den Variablen nicht vor
(anders als Komma, etc.)
o bei Speicherung als .txt gehen Daten verloren (z.B. Variablen- und
Wertelabels)
o Datei  Textdaten lesen  Datei auswählen
o vordefiniertes Format: nein, mit Trennzeichen
o Datumsvariable muss definiert werden
o nach „Fertigstellen“ erscheinen Daten, jedoch ohne Variablen- und
Wertelabels und ohne benutzerdefiniert fehlende Werte
 …aus Excel
 Datei  Öffnen  Daten  Dateityp Excel auswählen, Datei auswählen Öffnen
Variablendefinition in SPSS
Allgemeine Regeln der Benennung
 maximal 64 Zeichen (besser kürzere Namen)
 Beginn mit einem Buchstaben (@auch erlaubt)
 neben Buchstaben und Ziffern nur folgende Zeichen: _ . @ # $
 keine Leerzeichen
 letztes Zeichen kein Punkt oder Unterstrich
 Variablen dürfen nicht: ALL, AND, BY, EQ, GE, GT, LE, LT, NE, NOT, OR, TO, WITH heißen
 Namen dürfen nicht doppelt vergeben werden
 Kodierplan: ordnet einzelnen Fragen Variablennamen zu sowie den Merkmalsausprägungen
Codenummern
Variablen definieren
 Typ: Art der Variable z.B. numerisch (Zahlen), Datum (Format festlegen), String (Anzahl der
Zeichen festlegen
 Spaltenformat: =Breite (Zeichen inkl. Komma und Dezimalstellen)
 Variablenlabel: = Beschreibung der Variablen
 Wertelabels: Werte entsprechend dem Kodierplan benennen (z.B. 1=weiblich, 2=männlich)
 Fehlende Werte: beachten, dass nur Werte eingegeben werden, die in der Variablen sonst
nicht möglich sind (z.B. Alter = 999)
 systemdefiniert fehlende Werte
o Punkt in der Datenansicht wenn kein Wert eingegeben wurde
 benutzerdefiniert fehlende Werte
o Benutzer gibt Wert ein, der als fehlend behandelt werden soll
o Vorteil: Sicherheit, dass der Wert nicht vergessen wurde sondern fehlt
 Ausrichtung: Wo sollen Variablen im Datenfenster angezeigt werden?
 Messniveau
 Skala: metrische Variablen (intervall-/verhältnisskaliert), quantitative Eigenschaften
(Daten sind Zahlen, z.B. Körpergröße)
 Ordinal: geordnete Kategorien (Ratings)
 Nominal (ungeordnete Kategorien, z.B. Haarfarbe, Geschlecht und String-Variablen)
Übertragen von Definitionen auf andere Variablen
 Variableneigenschaften kopieren (Rechtsklick auf die linke Spalte & kopieren)
 in leere Zeile oder Zeile mit neuer Variablen einfügen
 ggf. Variablennamen und -label ändern
anschließend Dateneingabe nach Kodierplan in der Datenansicht
Überprüfung der Dateneingabe
fehlende Werte (missings)
 häufiges Problem bei ohnehin kleiner Stichprobe/N
 fehlende Werte können in drei Gruppen eingeteilt werden
 MCAR: missing completely at random
o Muster fehlender Werte ist völlig unvorhersehbar
 MAR: missing at random
o das Muster fehlender Werte lässt sich aus anderen Variablen im Datensatz
vorhersagen (außer der AV)
 MNAR: missing not at random
o Fehlen von Werten ist von der AV abhängig
o Generalisierbarkeit der Ergebnisse ist gefährdet

unbedenklicher Umgang mit den fehlenden Werten nur bei MCAR oder MAR
 Häufigkeit fehlender Werte anzeigen
 gesamte Häufigkeit
o Analysieren  Deskriptive Statistiken  Häufigkeiten
o Anzahl der fehlenden Werte wird in der Ausgabe angezeigt
 fehlende Werte einer Person
o neue Variable berechnen die dies angibt
o Transformieren  Variable berechnen  Zielvariable „miss“ nennen 
„Numerischer Ausdruck“: Nmiss (zu finden in Funktionsgruppe „Fehlende
Werte“), in Klammern dahinter Variablen(-bereich) angeben  OK
o neue Variable „miss“ absteigend sortieren (<10% fehlend/Person ok)
Umgang mit fehlenden Werten
 Ausschluss/Löschen
 Listenweiser Fallausschluss (Standard bei SPSS)
 Fallausschluss Test für Test
 Variablen mit fehlenden Werten löschen
 Personen mit fehlenden Werten löschen
 Problem: viele Daten gehen verloren !!!
 Ersetzen
 populäre, aber problematische Methoden
o durch Median ersetzen (ab Ordinaldatenniveau)
 Transformieren  fehlende Werte ersetzen  Methode: Median der
Nachbarpunkte  wichtig: Anzahl der Nachbarpunkte: ALLE
o durch Mittelwert ersetzen (ab Intervalldatenniveau)

Transformieren  fehlende Werte ersetzen  Methode: Mittel der
Nachbarpunkte
o

Regressionsersetzung (ab Intervalldatenniveau)
 Transformieren  fehlende Werte ersetzen  Methode: Linearer
Trend am Punkt  wichtig: Anzahl der Nachbarpunkte: ALLe
o Problem: Reduktion der Varianz
 evtl. durch Gruppenmittelwert, -median ersetzen
 Daten  Fälle auswählen  Missingersetzung für jede Gruppe
getrennt
bessere Methoden (hier nur genannt)
o Expectation Maximization (nur bei MCAR und MAR)
 Analysieren  Analyse fehlender Werte im Kästchen
„Schätzungen“ EM anklicken & vervollständigte Daten speichern
o Multiple Imputation/ Vervollständigung der Daten (für MCAR, MAR und
MNAR)
 Analysieren  Multiple Imputationen  fehlende Datenwerte
imputieren  Imputationen bei 5 lassen  neues Datenset erstellen
 in neuer Datei sind die Orginaldaten und 5 Datensets mit
ersetzten Variablen
o Ergebnisse der späteren Analysen (Regression) werden sowohl für jeden
einzelnen imputierten Datensatz als auch kombiniert ausgegeben
Extremwerte/Ausreißer/Outlier
 sehr unterschiedlich vom Rest der Daten
 beeinflussen die Güte des Modells, das wir auf die Daten „passen“
 Ergebnisse können nicht generalisiert werden
 Mögliche Ursachen:
 Inkorrekte Dateneingabe
 Fehlende Werte nicht gelabelt
 Ausreißer gehören nicht zu der untersuchten Population
 Allgemein:
 für spätere Analysen mit ungruppierten Daten (Regression, Faktorenanalyse, …)
Ausreißer im gesamten Datensatz suchen
 für Analysen mit gruppierten Daten (ANOVAs) nach Ausreißern getrennt in jeder
Gruppe suchen
 Univariate Ausreißer identifizieren
 extremer Wert auf einer Variablen
 bei kontinuierlichen Variablen: über z-Werte (z.B. z >|3,29|; p> .001,zweiseitiger
Test)
o Analysieren  Deskr. Statistiken  Deskriptive  “standardisierte Werte als
Variable speichern“ anklicken  man erhält im Datenfenster z-Werte der
Variablen  im Datenfenster sortieren oder über Häufigkeiten analysieren
 Achtung: bei z-Werten Stichprobengröße beachten
o
bei sehr großen
Stichproben
werden durchaus
einige Werte mit
z >|3,29| erwartet


 wenn man davon ausgeht, dass Daten
Standardnormalverteilung folgen, können durch z-Transformation die Eigenschaften
dieser genutzt werden
o 95% der Werte liegen zwischen +/- 1,96
o 99% der Werte liegen zwischen +/- 2,58
o 99,9% der Werte liegen zwischen +/- 3,29
o nur wenige Werte liegen außerhalb dieser Werte
Werte mit großem z-Wert sollten also nur selten auftreten
o Zeichen für Extremwert
neben z-Werten auch Boxplots nützlich
o Diagramme  Diagrammerstellung  unten links Boxplot auswählen &
oben rechts ins Fenster ziehen oder veraltete Dialogfelder
o einfacher Boxplot (1 Variable auf x-Achse, evtl. 1 Gruppierungsvariable auf
Kategorienachse)
o gruppierter Boxplot (1 Variable auf x-Achse, 2 Gruppierungsvariable auf
Kategorienachse)
 Univariate Ausreißer beheben



richtig eingetippt und fehlende Werte gelabelt?
Ausschluss des Falls (nur, wenn nicht Teil der untersuchten Population)
Veränderung des Ausreißerwertes:
o Ersetzen durch den höchsten/niedrigsten Wert +/- 1
o Ersetzen durch Mittelwert +/- 2 oder 3 Standardabweichungen
o Wichtig dabei: Ausreißer muss nach wie vor der größte/kleinste Wert sein!
SPSS-Syntax
Definition
 “predefined written commands that instruct SPSS what you would like it to do”
 Befehle, die SPSS versteht
Möglichkeiten der Eingabe
 Eintippen per Hand
 Kopieren aus anderen Dateien
 über “Einfügen” aus dem Menü
Vorteile der Syntax




leichtes Speichern des Analyseablaufes
einfaches Labeln von Datensätzen, die aus Datenbanken abgerufen werden
Kommentare können eingefügt werden
für kleine Änderungen in der Analyse muss nicht das ganze Menü wieder durchgeklickt
werden: Änderungen können direkt in der Syntax gemacht werden
 SPSS gibt an, wenn sich doch mal Fehler in die Syntax einschleichen
 Öffnen des Syntax-Editors: Datei  Neu  Syntax
Syntax-Regeln






jeder Befehl beginnt in einer neuen Zeile
jeder Befehl endet mit einem Punkt
Unterbefehle werden mit einem Schrägstrich (/) voneinander getrennt
Text für Labels wird in Apostrophe gesetzt
Dezimaltrennzeichen in der Syntax ist immer ein Punkt
Hilfe und Beispiele gibt es (auch) unter: Hilfe  Befehlssyntax-Referenz
 Syntax wird ausgeführt über : Ausführen  Auswahl/Alle/… oder mit grünem Pfeil
 Kommentare beginnen mit einem Sternchen und enden mit einem Punkt (SPSS ignoriert sie
dann)
 Fehler/unvollständige Befehle werden direkt in roter Schrift angezeigt oder nach Versuch der
Ausführung (im unteren Teil der Syntax und in der Ausgabe)
 Text der Syntax findet sich auch in der Ausgabe
Datensätze teilen
 zum Beispiel: Analysen für Frauen und Männer getrennt durchführen
 Daten  Datei aufteilen  Gruppen vergleichen anklicken  Variable „Geschlecht“ ins
Fenster ziehen
 Syntax:
 SORT CASES BY geschl.
SPLIT FILE LAYERED BY geschl.
Fälle auswählen
 zum Beispiel: nur Einbezug von Psychologiestudenten in Analysen
 Daten  Fälle auswählen  “Falls Bedingung zutrifft“ auswählen  Falls  Bedingung
definieren
 nicht ausgewählte Fälle werden gestrichen
 Syntax:


USE ALL sorgt dafür, dass alle Fälle berücksichtigt werden
COMPUTESPSS berechnet neue Variable (filter_$), die für alle mit studium=1
(Psychos) den Wert 1 annimmt, für andere 0
 VARIABLE LABELS benennt diese Variable
 VALUE LABELS benennt die Werte mit 1=ausgewählt, 0=nicht ausgewählt
 FORMATS gibt das Format der neuen Variablen an
 FILTER filtert den Datensatz (alle Fälle mit dem Wert 0 werden aussortiert)
 EXECUTE Transformationen und Variablenberechnungen werden erst nach diesem
Befehl ausgeführt
 auch Möglichkeit Fälle etwa nach Alter auszuwählen (alter < 22) oder nach mehreren
Bedingungen (mit AND angehängt)
 wichtige Syntax- Befehle für Berechnungen
Variablen berechnen
 Beispiel: Summenscore für Ängstlichkeit in einem psychologischen Test berechnen
 Transformieren  Variable berechnen  Zielvariable definieren  aus
Funktionsgruppe „Statistisch“ SUM wählen, in Klammer entsprechenden Items (mit
Komma getrennt) einfügen
 unter Typ & Label kann ein Label eingegeben werden
 Syntax
 berechnen wenn fehlende Werte vorliegen
 z.B. wenn Summenscore auch bei 6 von 7 Werten berechnet werden kann
o fehlender Wert wird durch Mittelwert der anderen Werte ersetzt
 Mittelwert der 6 oder 7 vorhandenen Werte nehmen, den dann mit 7 multiplizieren
 Differenz berechnen
 z.B. Berechnung der Dauer von Erkrankung
 Transformieren  Variable berechnen  Zielvariable definieren  Differenz über „-“
zwischen den Variablen
 Syntax:
 Berechnungen mit Datumangaben
 Zeitdauern z.B. zwischen T1 und T2
 Transformieren  Assistent für Datum und Uhrzeit  Berechnen mit Datums- und
Zeitwerten durchführen  Berechnen der Anzahl der Zeiteinheiten…  Daten
eingeben (späteres zuerst!)  neue Variable benennen
Variablen umkodieren
 zum Beispiel: Überführung von Alter bei Erkrankung in kategoriale Variable
 Transformieren  Umkodieren in eine andere Variable
 Variablenlabels müssen nachträglich eingefügt werden
 Syntax
 neue Variable, die anzeigt, ob Wert fehlt
o Transformieren  Umkodieren in eine andere Variable
 erfassen manche Items positive und andere negative Verhaltensweisen, muss eine Art
umgekehrt/rekodiert werden
o Transformieren  Umkodieren in eine andere Variable
o für jede Variable einzeln, sehr umständlich
 schneller
mit
Syntax
Count-Funktion
 Auftreten eines/mehrerer bestimmter Fälle kann fallweise gezählt werden
 Transformieren  Werte in Fällen zählen  Variablen eingeben die gezählt werden
sollen und Werte deren Auftreten gezählt werden soll definieren
 Syntax:
Deskriptive Statistiken
 dazu zählen etwas: arithmetisches Mittel, Median, Modus, Varianz, Standardabweichung,
Schiefe, Exzess….
 Analysieren  Deskriptive Statistiken  Deskriptive Statistiken/Häufigkeiten/Explorative
Datenanalyse
 Mittelwert, Minimum
und Maximum
 Minimum/Maximum
nach Geschlecht
getrennt
 Quantile,
Schiefe und
Kurtosis
 minimaler, maximaler, durchschnittlicher z-Wert
 Analysieren  Deskriptive Statistiken  Deskriptive Statistiken, dort „Standardisierte
Werte als Variable speichern“ anklicken, für diese z-Werte dann wiederum
Deskriptive ausgeben lassen
Überprüfung von Verteilungsannahmen
 wichtige Verteilung z.B. Gleichverteilung, Normalverteilung
 Prüfung durch
 deskriptive Statistiken
 Plots / Prüfung durch Augenschein
 statistische Tests
Signifikanztestung
 getestet werden statistische Hypothesen (Aussagen über eine Population)
 bei einem statistischen Test werden 2 Hypothesen unterschieden
 die Nullhypothese, symbolisiert durch H0 (kein Unterschied)
 die Alternativhypothese, symbolisiert durch H1 (Unterscheid besteht)
 Null- und Alternativhypothese schließen sich wechselseitig aus, d.h. sie können nicht
gleichzeitig gelten
 zur Prüfung der Hypothese wird der Wert einer Statistik berechnet (empirischer Wert)
 fällt dieser Wert in einen Bereich, der bei Gültigkeit der Nullhypothese unwahrscheinlich ist,
entscheidet man sich gegen die Nullhypothese (verwirft sie) und nimmt stattdessen die
Alternativhypothese an
 Wahrscheinlichkeit, ab der man die Nullhypothese ablehnt, heißt Signifikanzniveau
(auch α-Niveau)
 üblicherweise auf 5% oder 1% festgelegt
 „unwahrscheinlich“ ist jedoch nicht „unmöglich“
 SPSS gibt für Signifikanztests p-Wert an
 p-Wert  Irrtumswahrscheinlichkeit  Wie wahrscheinlich ist das beobachtete
Ereignis (der empirische Wert) unter der Bedingung, dass die Nullhypothese zutrifft?
 für die Testentscheidung müssen diese mit dem (von uns) gesetzten α-Niveau verglichen
werden:
 Ist p < α so wird die Nullhypothese verworfen
 Ist p > α wird die Nullhypothese beibehalten
 Wichtig: Immer im Hinterkopf behalten, welche Hypothesen gerade getestet werden! (und
welche die Wunschhypothese ist)
Merke:
signifikant: unter 5%  H0 wird verworfen
nicht signifikant: über 5%  H0 wird beibehalten
Signifikanz = Irrtumswahrscheinlichkeit
 Irrtumswahrscheinlichkeit H0 zu verwerfen, obwohl sie richtig ist !!!
Prüfung auf Gleichverteilung
 deskriptiv: Werte sollen in jeder Kategorie (etwas) gleich häufig vorkommen
 visuell: Histogramm , Balken sollten (etwa) gleich hoch sein
 statistische Tests: Binominaltest, Chi-Quadrat-Test, KS-Test auf Gleichverteilung
 kategoriale Variable mit mind. 2 Ausprägungen


Binominal-Test auf Gleichverteilung
o Besteht ein signifikanter Unterschied zwischen den Häufigkeiten der beiden
Merkmalsausprägungen?
o z.B. Geschlecht im Datensatz Musikfestival
Analysieren  Nichtparametrische Tests Alte Dialogfelder  Binominal
 kategoriale Variable mit mind. 3 Ausprägungen


Chi-Quadrat-Test auf Gleichverteilung
o Unterscheiden sich beobachtete und erwartete Häufigkeiten bei
nominalskalierten Variablen signifikant voneinander?
o Bsp. 3000 x Würfeln (Datensatz: Wuerfel.sav)
2 Schritte, da hier Werte und deren Häufigkeiten als Fälle angegeben
sind:
o Daten  Fälle gewichten  n als Gewichtungsvariable eingeben
o Analysieren  Nichtparam. Tests  Alte Dialogf. Chi-Quadrat
 stetige Variablen
 K-S-Test auf Gleichverteilung
o Analysieren  Nichtparametrische Tests  Alte Dialogfelder  K-S bei einer
Stichprobe  „Testverteilung“: Gleichverteilung
Exakte Tests
 im Menü unter „Exakt“ 3 Möglichkeiten:
 nur asymptotisch (Voreinstellung bei SPSS)
o Sinnvoll bei großen Stichproben
o nimmt eine bestimmte Verteilung für die Statistik an (hier die Chi-QuadratVerteilung)
 Exakt
o SPSS kann die Irrtumswahrscheinlichkeit auch genau berechnen
o ohne Verteilungsannahmen
o ABER: je größer die Stichprobe, desto komplexer ist die Berechnung und
desto länger braucht SPSS (Zeitlimit)
 Monte Carlo
o Alternative zu exakte Tests (wenn Stichprobe zu groß)
o nimmt eine ähnliche Verteilung wie in der Stichprobe, zieht daraus viele
Stichproben (Voreinstellung: 10 000), aus denen dann die Signifikanz
einschließlich Konfidenzintervall berechnet wird
Prüfung auf Normalverteilung
 deskriptiv
 M, Md, Mo fallen ungefähr zusammen
 Exzess/Kurtosis innerhalb [-1;1]
 Schiefe innerhalb [-.5;.5]
o Exzess und Schiefe besser über z-Werte beurteilen:
 Kriterium für „Signifikanz“ (Normalverteilung nicht gegeben)
o In kleinen Stichproben: 1.96 (p<.05)
o In mittleren Stichproben: 2.58 (p<.01)
o In großen Stichproben: 3.29 (p<.001)
 visuell
 Histogramm mit überlagerter Normalverteilungskurve
 Boxplot
 Q-Q-Diagramm
 statistische Tests


KSA-Test: Kolmogorov-Smirnov-Anpassungstest auf NV
o testet die empirisch ermittelten Werte gegen die bei einer NV zu
erwartenden Werte
o Annahme: Populationsstreuung und -mittelwert sind bekannt
o Normalfall: beides ist nicht bekannt, muss aus den Daten geschätzt werden
 in dem Fall Lilliefors-Korrektur anwenden
signifikanter p-Wert spricht für die Abweichung von der NV-Annahme (H0:
Normalverteilung liegt vor Wunschhypothese)
 zu beachten vor allem bei großen Stichproben:
 KSA-Test ist stichprobengrößensensitiv
o deshalb nicht geeignet für große Stichproben (N > 200)
o da er dann bereits bei relativ unbedeutenden Abweichungen von der
Normalverteilung signifikant wird!
 nie nur auf den KSA-Test verlassen, immer Diagramme und deskriptive Statistiken
anschauen
 2 Wege zum KSA-Test in SPSS:

Analysieren  Nichtparametrische Tests  Alte Dialogfelder K-S bei einer
Stichprobe „Testverteilung“: Normalverteilung
o nicht zu empfehlen, da keine Lilliefors-Korrektur

Analysieren  Deskriptive  Explorative Datenanalyse  unter Diagramme
„Normalverteilungsdiagramme mit Test“ anklicken
o hier wird Lilliefors-Korrektur angewandt
 über diesen Pfad auch Q-Q-Plots (Quantil-Quantil-Plot: Quantile der Variablen werden gegen
die Quantile der Normalverteilung abgetragen  Punkte sollten auf der Diagonalen liegen)
 Beispiel für Stichprobengrößensensitivität
Transformationen
 Transformationen beheben starke Abweichungen von der Normalverteilung
 nicht nur eine, sondern alle Variablen transformieren
 da ursprüngliche Skalierung verloren geht
 besonders kritisch für Mittelwertsvergleiche (!)
 je nach Verteilung der ursprünglichen Variable sind
 verschiedene Transformationen möglich
 Transformieren  Variable berechnen  Transformieren  Variable berechnen
Arten von Hypothesen
 Zusammenhangshypothesen
 Gibt es Zusammenhänge zwischen zwei oder mehr Variablen?
 Lässt sich eine Variable durch eine oder mehrerer andere Variablen vorhersagen?
 Unterschiedshypothesen
 Gibt es Unterschiede zwischen mindestens zwei Gruppen in Bezug auf eine oder
mehrere Variablen?
Unterschiedshypothesen
 Wahl des Verfahrens ist abhängig vom Skalenniveau
Verfahren für Intervalldaten
 Unterscheiden sich zwei Gruppenmittelwerte?
 unabhängige Stichprobe
 Vergleichsgruppen bestehen aus unterschiedlichen Fällen, die unabhängig
voneinander aus ihren Grundgesamtheiten gezogen werden
 abhängige (gepaarte) Stichprobe
 Vergleichsgruppen bestehen aus denselben Untersuchungseinheiten, bei denen
bestimmte Variablen mehrfach erhoben wurden ODER die Untersuchungseinheiten
der Gruppen wurden nicht unabhängig erhoben (z.B. Mutter und Vater)
 Hypothesen
 (µ=Erwartungswert)
 ungerichtet = Unterschied
 gerichtet = z.B.
besser/schlechter
 t-Test für unabhängige Stichproben

jede Person nimmt nur an einer der zwei Experimentalbedingungen teil
(d.h. Messwerte = unabhängig)

Voraussetzungen
1. Unabhängigkeit der Stichproben und somit der Werte
2. mindestens Intervalldatenniveau
3. Normalverteilung der Stichprobenkennwerte (nicht der Daten)
4. Varianzhomogenität

zu 3. :
o nicht Daten an sich müssen normalverteilt sein, sondern
Stichprobenkennwerte (hier Mittelwerte)
o mit Hilfe der Daten und des zentralen Grenzwerttheorems werden
Rückschlüsse auf die Erfüllung gezogen
 Daten normalverteilt  Stichprobenkennwerteverteilung normal
 bei großen Stichproben (>30): Stichprobenkennwerteverteilung
normal, wenn Daten nicht normalverteilt
o zentrales Grenzwerttheorem:
 Theorem das besagt, dass die Stichprobenkennwerteverteilung des
Mittelwertes eine Normalverteilung um den Populationsmittelwert
bildet
 Stichprobenkennwerteverteilung: aus einer Population werden
wiederholt gleichgroße Stichproben gezogen, dann wird die
Verteilung z.B. des Mittelwerts betrachtet

zu 4:
o
o
Varianz der AV ist für alle getesteten Gruppen gleich groß
Levene-Test
 prüft, ob die Varianzen der Gruppen sich unterscheiden
o H0: Varianzen sind gleich
o H1 : Varianzen sind nicht gleich
 Test signifikant = Varianzen nicht homogen = Voraussetzung ist nicht
erfüllt
 berichten:
o Die Varianzen der Variable X waren für die verschiedenen
Gruppen gleich, F(df1,df2)= Wert der Levene Statistik, n.s.
o Die Varianzen der Variable Y waren für die verschiedenen
Gruppen unterschiedlich, F(df1,df2)= Wert der Levene
Statistik, p<.05.
 Wobei:
 df1= Anzahl der Gruppen - 1
 df2= Anzahl der TN - Anzahl der Gruppen

Durchführung des Tests
o Beispiel: 12 Arachnophobiker spielen mit Spinne, 12 sehen Bilder, Messung
der Angst
o Analysieren  Mittelwerte vergleichen  t-Test
bei unabhängigen Stichproben  Testvariable
Anxiety, Gruppenvariable Group (diese mit 0 und
1 definieren)
o
o
zunächst Prüfung der Voraussetzung der Varianzhomogenität (Levene-Test)
 Bericht: Die Varianzen der
Variable Anxiety waren für
die beiden Gruppen gleich,
F(1,10)= 0,782, n.s.
es werden 2 t-Test Varianten
angegeben
o
o
o

SPSS testet zweiseitig: wenn einseitige Signifikanz gesucht ist p-Wert durch 2
teilen !!
Testbericht bei zweiseitiger/einseitiger Testung
o Durchschnittlich zeigten Teilnehmer beim Anblick einer echten Spinne
größere Angst (M= 47.00, SE= 3.18) als beim Anblick eines Spinnenbildes (M=
40.00, SE= 2.68).
o Dieser Mittelwertsunterschied erwies sich nicht als signifikant t(22)= -1.68,
p>.05 /p=.107 (zweiseitig)/p=.054 (einseitig)
 t-Test für abhängige Stichproben

alle Personen nehmen an beiden Experimentalbedingungen teil (d.h. Messwerte sind
abhängig

Voraussetzungen:
o mindestens Intervalldatenniveau
o Normalverteilung der Stichprobenkennwerte (nicht der Daten)
 hier: der mittleren Differenzen
 in kleinen Stichproben:
o Diese Differenz für jede Person berechnen (Messung1 Messung2)
o Differenz auf Normalverteilung prüfen

Durchführung des Tests
o 12 Arachnophobiker spielten mit Tarantel und sahen Bilder derselben,
Messung der Angst
o Analysieren  Mittelwerte vergleichen 
t-Test bei verbundenen Stichproben 
Variablenpaar „picture“ und „real“ als
gepaarte Variablen
o einzelne Werte, Mittelwerte und Standardabweichungen der einzelnen
Messungen sind identisch mit denen der unabhängigen Messungen,
stammen aber jeweils von den gleichen Personen

Ergebnisbericht bei zweiseitiger/einseitiger Testung:
o Die Teilnehmer zeigten beim Anblick einer echten Spinne signifikant größere
Angst (M= 47.00, SE= 3.18) als beim Anblick eines Spinnenbildes (M= 40.00,
SE= 2.68), t(11)= -2.47, p<.05 /p=.031 (zweiseitig)/p= .016 (einseitig).
 bei Verletzung der Voraussetzungen
 Normalverteilung:
o mehr Versuchspersonen rekrutieren
o evtl. Variablen transformieren
 Varianzhomogenität:
o Test für ungleiche Varianzen interpretieren

Alternativ: auf Tests für ein niedrigeres Datenniveau ausweichen
o T-Test für abhängige Stichproben  Wilcoxon-Test
o T-Test für unabhängige Stichproben  Mann-Whitney U-Test
Verfahren für Ordinaldaten
 beide Tests basieren auf dem Vergleich von Rangplätzen
 unterscheiden sich die gemittelten rangpostionen von zwei
 Mann-Whitney-U-Test für unabhängige Stichproben


jede Person nimmt nur an einer der Experimentalbedingungen teil (d.h. Messwerte
sind unabhängig)
Unterscheiden sich die gemittelten Rangpositionen von zwei unabhängigen
Gruppen?

Durchführung des Tests
o Beispiel: Auswirkung von Drogen auf Stimmung/Depression, Ecstasy vs.
Alkohol
o Ränge bilden
o
o
o
o
o
o
o
o
o
o
o
o
o
o
o
o
o
o
zur Veranschaulichung vorher deskriptive Statistiken ausgeben lassen,
Modus und Median vergleiche, anschließend Aufteilung der Datei wieder
entfernen
Analysieren  Nichtparametrische Tests  Alte Dialogfelder  Zwei
unabhängige Stichproben
 BDI_SO und BDI_MI als Testvariablen,
Droge als Gruppenvariable (Gruppen mit
1 und 2 definieren)
 bei kleiner Stichprobe exakte Testung
möglich







Ergebnisbericht (zweiseitige Fragestellung)
o Am Tag nach dem Konsum unterschieden sich die Depressionswerte der
Personen, die Ecstasy genommen haben (Md=17.50) nicht signifikant von
den Personen, die Alkohol getrunken haben (Md=16.00), U=35.50, z=-1.10,
n.s./p>.05. Am Mittwoch waren die Ecstasy-Konsumenten (Md=33.50)
jedoch signifikant depressiver als die Alkohol-Konsumenten (Md=7.50) ,
U=4.00, z=-3.48, p<.05.

andere nonparametrische Tests für unabhängige Stichproben
o Kolmogorov-Smirnov-Z: Prüft, ob zwei Stichproben aus der gleichen
Population gezogen wurden, vergleichbar mit dem Mann-Whitney-U-Test,
hat bei kleineren Stichproben (<25 pro Gruppe) größere Power
o Extremreaktionen nach Moses: Vergleicht die Variabilität der Werte in den
zwei Gruppen
o Wald-Wolfowitz-Sequenzen: Variante des Mann-Whitney-Test. Prüft, ob es
in der Rangreihe fortlaufende Sequenzen von Werten aus einer Gruppe gibt
 Wilcoxon-Test für abhängige Stichproben



alle Personen nehmen an allen Experimentalbedingungen teil (d.h. Messwerte sind
abhängig)
betrachtet die Differenzen von Messwertpaaren (ähnlich t-Test)
Durchführung des Tests
o Differenzen d berechnen
o Differenzen sortieren
o Nulldifferenzen entfernen. n ist die Anzahl der übrig bleibenden Differenzen
o Rangreihe der Absolutbeträge der Differenzen bilden. Die kleinste erhält
Rangplatz 1. Bei Rangbindungen das Verfahren der Durchschnitte verwenden
o Berechne die Summe der Rangplätze mit negativem Vorzeichen und die
Summe der Rangplätze mit positivem Vorzeichen. T ist die kleinere der
beiden Rangsummen.
o SPSS wandelt T in einen z-Wert um und gibt den p-Wert aus
o
o
um Analyse für beide Gruppen getrennt
durchzuführen, Datei zuvor aufteilen (über
Daten Datei aufteilen  Gruppen
vergleichen).
Analysieren  Nichtparametrische Tests  Alte
Dialogfelder  Zwei verbundene Stichproben
 BDI_SO und BDI_MI als Testpaar einfügen

Ergebnisbericht (zweiseitig)
o Für Ecstasy-Konsumenten waren die BDI Werte am Mittwoch (Md=33.50)
signifikant höher als am Sonntag (Md=17.50), T=0/z=-2.53, p<.05/p=.008.
o Für Alkohol-Konsumenten waren die BDI Werte am waren die BDI Werte am
Mittwoch (Md=7.50) signifikant niedriger als am Sonntag (Md=16.00),
T=8/z=-1.99, p<.05/p=.045

andere nonparametrische Tests für abhängige Stichproben
o Vorzeichentest: Betrachtet nur die Richtung, jedoch nicht die Größe der
Differenz  wenig Power
o McNemar: Für Nominaldaten (dichotom)  betrachtet Kategorienwechsel
o Rand-Homogenität: Erweiterung des McNemar für Ordinaldaten
Verfahren für Nominaldaten
 Binominaltest und χ2-Einzeltest



auch bei Prüfung auf Gleichverteilung
Analysieren  Nichtparametrische Tests  Alte Dialogfelder  Binominal bzw. ChiQuadrat  Testvariablen eingeben
kann jeweils die erwartete Verteilung (unter Annahme der H0) angegeben werden
(oft ist das die Gleichverteilung)
o Binominaltest: „Testanteil“ gibt relative Häufigkeit der ersten Kategorie
wider
o χ2-Einzeltest : Relative Häufigkeiten können als „Erwartete Werte“
eingegeben werden
 4-Felder- χ2-Test

Vergleich zweier zweifach gestufter Merkmale

Voraussetzungen
o Unabhängigkeit der Daten
 jede Person taucht nur in einer Zelle auf
 d.h. 4-Felder χ² kann nicht an Messwiederholungsdaten
durchgeführt werden  McNemar Test
o erwartete Häufigkeit pro Zelle sollte immer > 5 sein

Durchführung des Tests
o Beispiel: Katzen das Tanzen beibringen mit Streicheln oder Futter als
Belohnung
o Darstellung der Daten in eine Kreuztabelle/Kontingenztabelle
o
o
Analysieren  Deskriptive Statistiken  Kreuztabellen

o
o
standardisierte Residuen geben Unterschied zwischen beobachteten und
erwarteten Häufigkeiten in Form von z-Werten wieder
 Vergleich mit kritischen z-Werten (z.B. 1,96) zeigt, welche Residuen
signifikant sind
 im Beispiel fallen beide Residuen der Futterbedingung auf
Ergebnisbericht
 Es zeigte sich ein signifikanter Zusammenhang zwischen der Art des
Trainings und der Tanzfähigkeit χ²(1)= 25.36, p< .001.
 k*l – χ2 –Test



entspricht dem 4-Felder-χ2-Test
kategoriale Variablen sind jedoch nicht nur zweistufig, sondern mehrstufig
Auch hier kann der exakte Fisher-Test als Alternative genutzt werden, wenn die
erwarteten Zellenhäufigkeiten gering sind
o muss unter „Exakt“ ausgewählt werden
o bei großen Stichproben dauern exakte Tests sehr lang oder können nicht
berechnet werden
Prüfen von Zusammenhängen
Lineare Regression
 Definition Regression:
 Vorhersage einer Variablen (Kriterium) aufgrund einer oder mehrerer anderer
Variablen (Prädiktoren)
o Prüfung von Kausalhypothesen
o sowohl Prädiktoren als auch Kriterien sind intervallskaliert
 Einfache Regression
 1 Kriterium wird durch 1 Prädiktor vorhergesagt
 Multiple Regression:
 1 Kriterium wird durch mehrere Prädiktoren vorhergesagt
 typische Fragestellung einer einfachen linearen Regression:
 Wie wirkt sich der Prädiktor (z.B. Arbeitszufriedenheit) auf das Kriterium (z.B.
Arbeitsleistung) aus? Kriterium (z.B. Arbeitsleistung) aus?
o „Stärke“ des Zusammenhangs  Korrelation
 ABER: Korrelation ≠ Kausalität
o Zusammenhänge können auch durch andere Einflüsse verursacht werden!
(z.B.: Storchensichtungen und Anzahl der Schwangerschaften)
 linearer Zusammenhang zweier Variablen lässt dich in einem Streudiagramm darstellen
 Regression ist der Versuch, eine Gerade durch die Punktewolke zu legen, für die die
Summe der quadrierten vertikalen Abstände von den einzelnen Messpunkten
minimiert wird
o Minimierung der Vorhersagefehler
 hinter der Regressionsgeraden steht ein Modell, das den (linearen) Zusammenhang zwischen
Prädiktor und Kriterium beschreiben soll
 Einfache lineare Regression

bei standardisierter Form:
o β1  b1 (liegt im Bereich von -1 bis +1)
o b0  verschwindet, da standardisierte Gerade durch den Ursprung führt
Lineare Regression: Güte des Modells
 Wie gut passt das Modell auf die Daten?
 Determinationskoeffizient R2


im Falle der einfachen Regression entspricht R2 der
quadrierten Korrelation zwischen Prädiktor und
Kriterium
QS = Quadratsumme: quadrierte, über alle Fälle aufsummierte Abweichung …
o
… der beobachteten y-Werte vom Mittelwert y  QSTotal
o
… der vorhergesagten y- Werte vom Mittelwert y  QSRegression
o
… der beobachteten y-Werte von den vorhergesagten  QSResiduum
 F-Test der linearen Regression
 wenn signifikant: Vorhersage durch den Prädiktor ist besser als eine Vorhersage
durch den Mittelwert des Kriteriums
 Bewertung der Prädiktoren (bei einfacher Regr.: des Prädiktors)
 wenn signifikant: Regressionsgewicht des Prädiktors ungleich Null und der Prädiktor
trägt bedeutsam zur Vorhersage bei
Lineare Regression: Voraussetzungen
 Linearität des Zusammenhangs zwischen Prädiktor und Kriterium
 Prüfung der Linearität:
o Betrachten des Streudiagramms
o hoher Anteil der erklärten Variation spricht für linearen Zusammenhang
 Homoskedastizität: Varianz der Residuen muss auf jedem Level des Prädiktors gleich sein
 Normalverteilung der Residuen
 Unabhängigkeit der Residuen
 Prüfung der Annahmen bzgl. der Residuen
o QQ-Plot der Residuen
o Histogramm der Residuen mit überlagerter NV-Kurve
o Scatterplot: standardisierte Residuen vs. standardisierte vorhergesagte
Werte (Residuen sollen unsystematisch um horizontale Nulllinie schwanken)
Lineare Regression in SPSS
 Beispiel: Anzahl Plattenverkäufe soll aus Werbebudget vorhergesagt werden
 Analysieren  Regression Linear
o Record Sales als AV (Kriterium)
o Advertising Budget als UV (Prädiktor)
 zur Prüfung der Annahmen bzgl. Residuen 
Diagramme
o Streudiagramm mit ZRESID auf Y-Achse,
ZPRED auf X-Achse
o Unter „Diagramme der standardisierten
Residuen“ Histogramm anklicken
o
o

Regressionskoeffizient B unstandardisiert
 (Konstante) b0
 Advertising Budget  b1
Standardisierte Koeffizienten Beta
 Advertising Budget β1
Bewertung des Prädiktors: t-Test
o Der t-Test für den Prädiktor ist signifikant, sein Regressionsgewicht
unterscheidet sich signifikant von Null
o SPSS gibt auch einen Test aus, der die Konstante (Achsenabschnitt) darauf
testet, ob sie sich von Null unterscheidet für uns irrelevant!
o
Residuen streuen im linken Teil stärker um die Nulllinie als im rechten
 spricht gegen Homoskedastizität
 Lineare Regression berichten

in Tabellenform

Regressionsgleichung aufstellen
Einfaktorielle Varianzanalyse
 Prüfung von Unterschiedshypothesen bei mehr als 2 Gruppen (anstelle des t-Tests für
unabhängige Stichproben)
 Arten von Varianzanalysen:
 Einfaktoriell: 1 Faktor/UV/Gruppierungsvariable
 Zwei- bzw. mehrfaktoriell: 2 oder mehr UVs  Prüfen von Haupt- und
Interaktionseffekten
 Kovarianzanalyse: Berücksichtigung eines weiteren (metrischen) Einflussfaktors
 Mit Messwiederholung: Berücksichtigung wiederholter/abhängiger Messungen
 Multivariate Varianzanalyse: Berücksichtigung mehrerer AVs
 Warum beim Vergleich von mehreren Gruppen nicht mehrere t-Tests rechnen?
 Wahrscheinlichkeit für einen Fehler 1. Art würde sich für die gesamte Testung
erhöhen!
 Bsp.: 3 Gruppen mit 3 t-Test vergleichen
o Für jeden Test ist die Wahrscheinlichkeit, einen Fehler 1. Art zu machen 5%,
die Wahrscheinlichkeit für keinen α-Fehler beträgt 95%
o Wie groß ist die Wahrscheinlichkeit, bei drei (unabhängigen) Tests
mindestens einen α-Fehler zu machen?
 P (kein α-Fehler) = 0.95 x 0.95 x 0.95 = 0.953 = 0.857
 P (mind. 1 α-Fehler) = 1-P(kein α-Fehler) = 1-0.857 = 0.143
 Die Wahrscheinlichkeit beträgt 14,3%!
o Familywise Error
Einfaktorielle ANOVA - Grundprinzip
 ANOVA (analysis of variance) vergleicht Varianzen (mit dem Ziel, Mittelwertsunterschiede
zwischen den Gruppen zu finden)
 Varianz = Quadratsumme / Freiheitsgrade
 Gesamtvarianz = Treatment- + Fehlervarianz
 Treatmentvarianz (Varianz zwischen den Gruppen): Abweichung der Faktorstufenmittel vom
Gesamtmittel
 Fehlervarianz (Varianz innerhalb der Gruppen): Abweichung der Einzelwerte vom
Faktorstufenmittel
 F-Test prüft, ob Treatmentvarianz signifikant größer ist als Fehlervarianz (in dem Fall:
Gruppenmittelwerte unterscheiden sich, Treatment wirkt)
 Beispiel:
o Ein neues Medikament zur Behandlung von Depressionen wurde getestet. Gruppe 1
bekam ein Placebo (Kontrollgruppe). Gruppe 2 bekam die einfache Dosis, Gruppe 3
die doppelte Dosis. Abhängige Variable sind die Werte in einem
Depressionsfragebogen (hohe Werte = stark ausgeprägte Depression).
 F-Test zeigt an, ob es einen Unterschied zwischen den untersuchten Gruppen gibt
 zeigt jedoch nicht an, welche Gruppen sich konkret voneinander unterscheiden
 dafür weitere Analysen:
o Geplante (a priori) Kontraste
 Wenn vorher bereits spezifische Hypothese vorliegen
 Anstelle der ANOVA
o Post hoc Tests
 Alle Gruppen werden miteinander verglichen, jedoch können hier
Korrekturen angewandt werden, damit der familywise error .05
niemals übersteigt
 A-Priori-Kontraste


Kontraste vergleichen bestimmte Gruppen/Sets von Gruppen und teilen die
Treatmentvarianz dadurch in verschiedene Anteile auf
Es werden 2 grundlegende Arten von Kontrasten unterschieden
o Orthogonale Kontraste
 Die Treatmentvarianz wird in unabhängige Teile aufgeteilt
o Nicht orthogonale Kontraste



Die Teile an Treatmentvarianz, die durch die Kontraste aufgeklärt
werden, überschneiden sich teilweise
Orthogonale A-Priori-Kontraste

Konstruktionsregeln:
o Anzahl der Kontraste ist Anzahl der Gruppen -1
o Die Varianz wird in unabhängige Teile aufgeteilt, d.h. wurde eine Gruppe
herausgegriffen, kann sie in keinen weiteren Kontrasten auftauchen
o Jeder Kontrast vergleicht nur 2 Varianzteile
o Gruppen mit positiven Gewichten werden mit Gruppen mit negativen
Gewichten verglichen
o Das Gewicht, der Gruppe(n) eines Varianzanteils = Anzahl der Gruppen im zu
vergleichenden Varianzanteil
o Gruppen, die nicht im Kontrast vertreten sind, bekommen das Gewicht 0
o Die Summe der Gewichte in einem Kontrast ist 0
o
o
Tabelle hilfreich für Eingabe in SPSS
Bei orthogonalen Kontrasten muss
 jede Kontrastsumme = 0 sein und
 die Summe der Kontrastprodukte = 0 sein

Nicht-orthogonale A-Priori Kontraste
o
bei nicht-orthogonalen Kontrasten muss
 jede Kontrastsumme = 0 sein
 die Summe der Kontrastprodukte ist jedoch ≠0

polynomiale A-Priori Kontraste
 Post hoc Tests



Nachdem der F-Test signifikant wurde
vergleicht jede Gruppe mit jeder anderen, sollte darum den α-Fehler kontrollieren
SPSS bietet viele verschiedene Post hoc Tests an:
o Nach Field (2009) sind bei gleichen Stichproben und gleichen Varianzen R-EG-W-Q und Tukey gut (gute Power, enge Kontrolle über Typ-I-Fehler)
o Garantierte Kontrolle über den Fehler 1. Art liefert Bonferroni, ist aber sehr
konservativ
o Bei leicht unterschiedlichen Gruppengrößen: Gabriel
o Bei sehr unterschiedlichen Gruppengrößen: Hochberg‘s GT2
o Bei unterschiedlichen Varianzen: Games-Howell
Einfaktorielle ANOVA in SPSS
 Voraussetzungen
 Intervallskalierung der AV
o Unabhängigkeit der Messungen
 Normalverteilung der AV  innerhalb der Gruppen
o Prüfen, wenn einzelne Gruppen mit ca. n < 30 besetzt sind(Diagramme,
Schiefe, Exzess, KSA-Test)
o bei gleicher Gruppengröße ist ANOVA recht robust
 Varianzhomogenität durch Levene-Test prüfen (wird in SPSS mit ausgegeben)
 Ausführung
 Analysieren  Mittelwerte vergleichen  Einfaktorielle ANOVA
o UV (Faktor) = Dosis
o AV = Leistung
o unter Optionen: Deskriptive,
Levene-Test
o Levene-Test
 p=.913 kleiner als α
=.05
 Test ist nicht
signifikant
 H0 wird beibehalten
 Varianzen sind homogen
o wenn Varianzen nicht homogen
 bei gleich Stichproben robust gegenüber fehlender
Varianzhomogenität
 Alternativ Welch‘s F berichten (besser als Brown-Forsythe F)
o
o
o

Zwischen den Gruppen = Treatment
Innerhalb der Gruppen = Fehler
Der F-Test ist signifikant (p=.025/p<.05), die Gruppen unterscheiden sich
voneinander
Welche Gruppen unterscheiden sich?  Post-hoc-Test
o
o

Jede Gruppe wird mit jeder verglichen
Je nach Test wird der p-Wert auf unterschiedliche Art für die multiplen Tests
angepasst Hier: Nur der Unterschied zwischen Placebo und hoher Dosis ist
signifikant!
Ergebnisbericht
o Es ergab sich ein signifikanter Effekt des Medikamentes auf die Leistung in
einem Test, F(2,12) = 5.12, p= .25.
o Der Post-hoc-Vergleich nach Tukey zeigte, dass die Placebo- Gruppe
(M=2.20, SE=0.58) sich von der Gruppe mit hoher Dosis (M=5.00, SE=0.71)
unterschied (p=.021), nicht jedoch von der Gruppe mit niedriger Dosis
(M=3.20, SE=0.58)(p>.05). Die niedrige Dosis und die hohe Dosis
unterschieden sich ebenfalls nicht signifikant voneinander (p>.05).
 Ausführung von Kontrasten

Durchführung von Kontrasten bietet sich an, wenn man zwar Vermutungen hat die
ANOVA aber noch nicht ausgeführt hat

Über den Pfad „Mittelwerte vergleichen“ müssen die
Kontraste von Hand entsprechend der Tabelle
eingegeben werden:
o Koeffizienten (Gewichte) nach Reihenfolge der
Gruppen (Kodierung beachten) eingebe
o Für einen weiteren Kontrast auf „Weiter“
klicken



Bei zweiseitiger Testung (ungerichtete Hypothese) ist nur der erste Kontrast
signifikant
Da hinter den Kontrasten im Beispiel gerichtete Hypothesen stehen, kann man auch
einseitig testen, dann ist auch der zweite Kontrast signifikant (p-Wert durch 2 teilen
p=.033)
Ergebnisbericht
o Die geplanten Kontraste deckten auf, dass die Einnahme des Medikamentes
verglichen mit der Einnahme eines Placebos Leistung signifikant steigert,
t(12)= 2.47, p=.015 (einseitig/ 1-tailed). Die Einnahme einer hohen Dosis
steigerte Leistung signifikant im Vergleich mit der Einnahmen einer niedrigen
Dosis, t(12)= 2.03, p=.033 (einseitig/ 1-tailed).
 weitere Möglichkeit Kontraste ausgeben zu lassen
 Analysieren  Allgemeines lineares Modell  Univariat
o Hypothesen entsprechen dem Helmert-Kontrast (nach Auswahl auf
„ändern“)
o Ergebnisse werden anders dargestellt, Signifikanzen sind jedoch gleich
Zweifaktorielle Varianzanalyse
 Datenbeispiel: Beeinflusst Alkohol die Einschätzung physischer Attraktivität und gibt es da
einen Unterschied zwischen Männern und Frauen?
 Je 24 Frauen und Männer tranken unterschiedliche Mengen Alkohol (kein Bier, 2
Bier, 4 Bier).
 Im Anschluss wurde ihre Attraktivität durch 100 andere Personen bewertet (AV:
höherer Wert  attraktiver).
 2x3 Design [UVs: Geschlecht (2); Alkohol(3)]
 AV: Attraktivitätsrating der Person (durch 100 andere Pers.)

systematische Varianz in diesen Daten setzt sich zusammen aus der Varianz, die
aufgeklärt wird durch:
o Geschlecht (2 Gruppen): Männer und Frauen
o Alkohol (3 Gruppen): kein Bier, 2 Bier, 4 Bier
o Interaktionseffekt von Geschlecht und Alkohol: Männer ohne Bier, Männer
mit 2 Bier, … , Frauen mit 4 Bier
Interaktionseffekte
 Effekt, der allein dadurch entsteht, dass die Probanden unterschiedlichen
Versuchsbedingungs-Kombinationenzugeteilt sind
 Größe des Effekts des einen Faktors ist abhängig von der Stufe des anderen Faktors
 3 Typen von Interaktionen: Typ lässt sich mithilfe von Interaktionsdiagrammen erkennen
 ordinale Interaktion


Graphen verlaufen in beiden Diagrammen gleichsinnig (sie schneiden sich nicht)
sind Haupteffekte signifikant, können sie global interpretiert werden
o Personen ohne Alkohol werden immer als attraktiver eingestuft
o Männer werden immer als attraktiver eingestuft als Frauen
 disordinale Interaktion



Graphen verlaufen in beiden Diagramm gegensinnig
Haupteffekte können nicht global interpretiert werden
Ausprägung des Faktors B immer bei Interpretation des Effekts des Faktors A
berücksichtigen
 hybride Interaktion


Graphen verlaufen in einem Diagramm gleichsinnig, im anderen nicht
lediglich der Haupteffekt mit gleichsinnigen Graphen kann global interpretiert
werden
o Hier der Haupteffekt von A: A1 ist immer (auf jeder Stufe von B) höher als A2
Zweifaktorielle ANOVA
 Voraussetzungen (wie bei einfaktorieller)
 Intervallskalierung der AV
 Unabhängigkeit der Messungen
 Normalverteilung der AV innerhalb der Gruppen
 Varianzhomogenität
 Durchführung des Tests
 für einen ersten Überblick Balkendiagramme
o Gruppierte Balkendiagramme (zwei
Diagramme möglich)
 mit dem Mittelwert der
Attraktivität auf der Y-Achse
 Alkohol und Geschlecht auf XAchse bzw. als Clustervariable

Analysieren  Allgemeines lineares Modell  Univariat
o AV: Attraktivität
o Feste Faktoren: Geschlecht & Alkohol Konsum

Fester Faktor: alle Bedingungen, an denen der Forscher interessiert ist, wurden im
Experiment realisiert
o Bsp. Alkohol: kein Bier, 2 Bier, 4 Bier
o Nur für diese Bedingungen können die Ergebnisse generalisiert werden, nicht
auf andere Bedingungen (z.B. 3 Bier)
Zufallsfaktor: Die Bedingungen, die im Experiment realisiert wurden, stellen eine
Zufallsauswahl der möglichen (interessierenden) Treatmentbedingungen dar
o Ergebnisse können über die untersuchten auch auf andere Bedingungen
generalisiert werden


Schaltfläche „Diagramme“ (liefert Interaktionsdiagramme)
o bei zwei Faktoren sind 2 Diagramme möglich:
 jeweils 1 Faktor auf „Horizontale Achse“ und „Separate Linien“
 „Hinzufügen“ klicken, dann umgekehrt

Post-hoc Tests
o nur für Faktoren mit >2 Stufen sinnvoll (hier: Alkohol)

Die angeforderten Tests, Diagramme
und Optionen lassen sich in der
Syntax wiederfinden
POSTHOC (-Tests), PLOT
(Diagramme), PRINT(Optionen)
DESIGN gibt an, dass beide
Haupteffekte und die Interaktion auf
Signifikanz getestet werden
o Gesättigtes Modell (alle möglichen
Effekte werden geprüft)
Levene Test: Es werden alle 6 Gruppen (2x3
Bedingungen) verglichen
o p=.202 >.05 Test ist n.s.
(Voraussetzung erfüllt)



o
Post-hoc Test nur interpretieren, wenn entsprechender Haupteffekt signifikant
 Der Unterschied zwischen kein Bier und 4 Bier und zwischen 2 Bier und 4 Bier
ist signifikant (nicht jedoch kein Bier zu 2 Bier)
o
Interaktionsdiagramme: hybride Interaktion, linkes Diagramm gleichsinnig, rechtes
nicht
o
Simple Effects
 aus Post-hoc-Tests lässt sich ablesen, welche Gruppen sich unterscheiden,
jedoch nur Haupteffekte
 Simple Effects Analysen können die Interaktion näher untersuchen (nur über
die Syntax):


prüft für jede Faktorstufe von „Alkohol“, ob es einen Geschlechtseffekt gibt
jedoch ohne α-Fehler-Adjustierung kann nachträglich „von Hand“
vorgenommen werden
 nur bei 4 Bier Unterschied zwischen Männern und Frauen
 Ergebnisbericht
o Es gab einen signifikanten Haupteffekt der Alkoholmenge auf die Attraktivität des
gewählten Partners, F(2,42)= 20.07, p< .001.
o Der Bonferroni Post-hoc-Test zeigte, dass die Attraktivität des gewählten Partners
nach 4 Bier signifikant geringer war als nach keinem Bier oder 2 Bier (beide p<.001).
Die Attraktivität des gewählten Partners nach 2 Bier unterschied sich nicht
signifikant von der Attraktivität nach keinem Bier (p>.05).
o Der Haupteffekt des Geschlechts auf die Attraktivität des gewählten Partners erwies
sich als nicht signifikant, F(1,42)=2.03, p=.16. D.h. Frauen und Männer wählten (bei
Nichtbeachtung der Alkoholmenge) gleich attraktive Partner aus.
o
o
o
Aus den Daten ergab sich ein signifikanter Interaktionseffekt zwischen Alkoholmenge
und Geschlecht auf die Partnerwahl, F(2,42)= 11.91, p<.001. Männer und Frauen
wurden durch Alkohol unterschiedlich in ihrer Partnerwahl beeinflusst.
Simple Effects Analysen zeigten, dass die Attraktivität der gewählten Partner gleich
war für Frauen (M= 66.88, SD= 10.33) und Männer (M= 60.63, SD= 4.96), die keinen
Alkohol tranken, sowie für Frauen(M= 62.50, SD= 6.55) und Männer (M= 66.88,
SD= 5.52), die 2 Bier tranken. Nach 4 Bier war die Attraktivität des gewählten
Partners für Frauen (M= 57.50, SD= 7.07) signifikant höher als und für Männer (M=
35.63, SD= 10.84).
Exkurs α-Justierung
 Bonferroni-Korrektur:
o Bei der Bonferroni-Korrektur zur Kontrolle des „familywiseerror“ wird das
ursprüngliche α-Niveau einfach durch die Anzahl der Tests geteilt und dann auf
diesem neuen α-Niveau getestet:
 α‘ = α/Anzahl der Test
 z.B. bei 3 Tests und ursprünglichem α-Niveau von 5%, α‘ = .05/3=.0167
 Alternative (da in SPSS der p-Wert angegeben ist):
o α-Niveau beibehalten, aber den p-Wert mit der Anzahl der Test multiplizieren (so
geht SPSS bei den Bonferroni-Post-hoc-Tests vor!)
Varianzanalyse mit Messwiederholung
 Mehrfache Messungen an denselben Personen
 „Erweiterung“ des t-Tests für abhängige Stichproben bei mehr als 2
Messungen/Messzeitpunkten
 Unterscheidung von:
 Innersubjektfaktoren: Veränderungen innerhalb der Personen
 Zwischensubjektfaktoren: Gruppenunterschiede
 Vorteil: Stabile Störvariablen (z.B Persönlichkeitsmerkmale) können statistisch kontrolliert
werden
 Nachteil: Sequenzeffekte
 ANOVA ohne Messwiederholung:
 Varianz innerhalb der Gruppen =
Fehlervarianz
 ANOVA mit Messwiederholung:
 Varianz innerhalb der Gruppen
wird nun interessant
o Aufteilung in erklärte
Varianz (durch
Messwiederholung) und
Residualvarianz

Problem: Messungen sind nicht unabhängig
 Neue Voraussetzung bei Messwiederholung: Sphärizität
o die Varianzen der Differenzen zwischen den verschiedenen
Messzeitpunkten/ Treatmentstufen sind gleich
o Varianz 1-2 ≈ Varianz 1-3 ≈ Varianz 2-3
 erst ab 3 Messungen ein Problem (da bei 2 Messungen nur 1 Differenz)
 Mauchley-Test auf Sphärizität
 falls signifikant, ist Sphärizität nicht gegeben (dabei auf Stichprobengröße achten)
 Bei Verletzung der Sphärizitäts-Voraussetzung:
 SPSS liefert weitere F-Tests mit korrigierten Freiheitsgraden
 Je stärker die Verletzung
o desto kleiner ist der Korrekturfaktor ε
o desto stärker weicht der korrigierte F-Test vom unkorrigierten ab
 Korrektur der Freiheitsgrade: Greenhouse-Geisser, Huynh-Feldt
 alternativ: Interpretation der multivariaten Tests, die SPSS automatisch mit ausgibt
 Durchführung des Test:
 Beispiel: Kinder bekommen Infos über neuartige Wesen, die in einer Box sitzen
(positive, negative oder neutrale). Gemessen wird die Angst der Kinder vor diesen
Wesen anhand der Zeit, die die Kinder benötigen, um in die Box zu fassen. Alle
Kinder nehmen an allen Bedingungen teil.
 Analysieren Allgemeines lineares Modell  Messwiederholung
o zunächst müssen die Innersubjektfaktoren (Messwiederholungsfaktor)
benannt und die Anzahl der Stufen festgelegt werden, dann folgt das
„übliche“ Fenster
o
o
Messwiederholungsstufen werden Zahlen zugeordnet (sinnvolle Anordnung)
unter Optionen Deskriptive Statistiken anfordern
 Test ist signifikant (p<.001): Voraussetzung wurde verletzt
 SPSS bietet 2 Korrekturen an
o Werte werden mit den df multipliziert, um so den F-Test zu korrigieren
o Greenhouse-Geisser Korrektur: wie stark weichen die Varianzen der
Differenzen voneinander ab?
 Je näher der Wert an 1, desto homogener sind die Varianzen der
Differenzen
 Je näher der Wert an der Untergrenze (1/k-1), desto heterogener
 Ist die Voraussetzung gebrochen, so sollte man den F-Test bei Greenhouse-Geisser
oder Huynh-Feldt ablesen (der F-Wert hat sich nicht verändert, nur die
Freiheitsgrade [df])
 SPSS gibt bei der ANOVA mit Messwiederholungunaufgefordert die Ergebnisse für
polynomiale Kontraste mit aus (Tabelle „Tests der Innersubjektkontraste“)
 In der Tabelle „Tests der Zwischensubjekteffekte“ werden die Ergebnisse von
Gruppierungsfaktoren (unabhängige Gruppen) ausgegeben, falls solche vorhanden
sind
o Im Tier-Beispiel könnte man z.B. das Geschlecht der Kinder als weiteren
Faktor untersuchen
o Das wäre ein gemischtes Design (mixed design) mit einem
Zwischensubjektfaktor (Geschlecht) und einem Innersubjektfaktor (Tier
Messwiederholung)
 Verletzung der Sphärizitätsvoraussetzung bringt auch für Post-hoc-Tests Probleme
o einige Post-hoc-Tests sind über „Optionen“  geschätzte Randmittel
zugänglich
o wird Sphärizität gebrochen, so ist Bonferroni der robusteste Post-hoc-Test.
o Sidak ist weniger konservativ als Bonferroni
 Interpretation wie „normale“ Post-hoc-Tests
o Hier: Unterschied zwischen negativ (1) und neutral (2), sowie negativ (1) und
positiv (3) ist signifikant
 Ergebnisbericht
 Der Mauchly-Test zeigte, dass die Voraussetzung der Sphärizität gebrochen wurde,
χ²(2)= 28.18, p<.001. Daher wurden die Freiheitsgrade mit Hilfe der GreenhouseGeisser Schätzung korrigiert, (ε=. 83).
 Eine einfaktorielle ANOVA mit Messwiederholung zeigte, dass die Art der Information
einen signifikanten Effekt auf die Annäherungszeit hatte, F(1.66,209.69)= 58.68,
p<.001.
 Bonferroni-korrigierte Post-hoc-Tests deckten signifikante Unterschiede in den
Annäherungszeiten zwischen neutraler und negativer Information, sowie positiver
und negativer Information (beide p<.001) auf. Dieser Unterschied ergab sich nicht
zwischen positiver und neutraler Information (p=.357).
Gemischtes Design
 Beispiel
 Ein klinischer Psychologe möchte die Wirkung eines neuen Antidepressivums namens
Cheerup untersuchen. 50 Patienten mit Depression werden randomisiert 5 Gruppen
zugewiesen:
o Wartelistenkontrollgruppe
o Placebo-Gruppe
o Seroxat (SSRI; selektive Serotonin-Wiederaufnahmehemmer)
o Effexor (SNRI; Serontonin-Noradrenalin-Wiederaufnahmeh.)
o Cheerup
 Das Ausmaß der Depression wurde vor der Behandlung und nach 2 Monaten
Behandlung erfasst (0=superglücklich bis 20=todtraurig).
 Durchführung des Tests
 Analysieren Allgemeines lineares Modell  Messwiederholung
o hier gibt es einen Messwiederholungsfaktor (vorher vs. nachher) sowie einen
Gruppierungsfaktor (Treatment)
o da es nur zwei Messzeitpunkt gibt dir der Mauchly-Test nicht berechnet
o
da es nur zwei Messzeitpunkt gibt dir der Mauchly-Test nicht berechnet
o
o
Über die beiden Zeitpunkte hinweg gibt es keinen Unterschied zwischen den
Treatments (p=.109)
 Die angeforderten Post-hoc-Tests dürfen darum nicht interpretiert werden
(diese sind auch alle nicht signifikant)
Interpretation der Interaktionsdiagramme
 Bei fast allen Treatments ist ein deutlicher Abfall in den Depressionswerten
zwischen T1 und T2 zu beobachten
 Ausnahme: No Treatment und evtl. Effexor
 Zu T1 (vorher) scheinen die Treatments sich nicht zu unterscheiden, aber zu T2


Diese Aussagen sind aber rein deskriptiv
Auch hier kann man mit Simple Effects Analysen die Interaktion näher
untersuchen