Die Fibonacci-Folge - Ihre Homepage bei Arcor

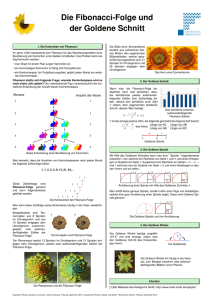
Schriftliche Hausarbeit
Thema der Arbeit:
Die Fibonacci-Folge
eingereicht von
Kiron Hussain
Geschwister-Scholl-Gymnasium
Klassenstufe 13
Abgabetermin: 08.07.2009
Fach: Mathematik
betreuende Lehrerin: Frau Rienhardt
Stuttgart, 01.07.2009
Inhaltsverzeichnis
Abb.: Leonardo Fibonacci
1.
Vorwort
2.
Leonardo Fibonacci
3.
Fibonacci-Folge
4.
Herleitung der Fibonacci-Folge
5.
Analogie zum Goldenen Schnitt
6.
Beispiele
7.
Nachwort
8.
Literaturverzeichnis
9.
Erklärung
2
1.
Vorwort
Der Themenkomplex, welcher sich um den Kern der Arbeit, namentlich der Fibonacci-Folge
rankt, ist ohne jeden Zweifel überaus gewaltig und vermag um seiner gerecht zu werden einer
mathematisch-objektiven Betrachtung, die jedoch aus naheliegenden Gründen hier einfach
den Rahmen sprengen würde. Diese bereits angesprochene Komplexität der zu betrachtenden
Materie rührt nicht zuletzt auch von ihrer interdisziplinären1 Charakteristik.
Ziel der Arbeit ist es daher eine möglichst adäquate, möglichst in sich geschlossene
Betrachtung der Fibonacci-Folge zu erzielen und zugleich besonderes Augenmerk auf die
mathematischen relevanten Aspekte zu werfen.
Kiron Hussain
2.
Leonardo Fibonacci
Leonardo Fibonacci, der italienische Kaufmann und Mathematiker wurde ungefähr um 1180
in Pisa geboren, weshalb er auch Leonardo von Pisa genannt wird. Da sein Vater als
Zollbeamter in der heutigen Bougie in Algerien tätig war, wurde Leonardo von einem
maurischen Privatlehrer unterrichtet. Von ihm erlernte er das arabische Zahlensystem und die
Grundlagen des kaufmännischen Rechnens. Er reiste viel und schrieb schließlich im Jahre
1202 sein „Liber abaci“ („Buch der Rechenkunst“), ein Werk, in dem er eben dieses
Zahlensystem und deren Berechnung erklärte.
Diese Veröffentlichung ist auch heute noch von großer Wichtigkeit, da es in der damaligen
Zeit zur Verdrängung der Römischen Zahlen geführt hat und dem heutigen Zahlensystem sehr
ähnlich ist. Seine Bekanntheit erlangte Fibonacci jedoch hauptsächlich durch die „FibonacciFolge“, die der französische Mathematiker Edouard Lucas erst später nach ihm benannte.
Gestorben ist Leonardo Fibonacci ungefähr 1240 in Pisa.
__________________________________________________________________________________
1 Unter Interdisziplinarität versteht man die Nutzung von Ansätzen, Denkweisen oder zumindest Methoden
verschiedener Fachrichtungen.
3
3.
Fibonacci-Folge
Die Fibonacci-Folge ist eine unendliche Auflistung von endlich oder unendlich vielen
fortlaufend nummerierten Objekten von Zahlen, bei der sich jedes neue Folgeglied aus der
Summe der beiden vorherigen Glieder ergibt.
Die Fibonacci-Folge ist durch das rekursive2 Bildungsgesetz mit den Anfangswerten
und
definiert.
Daraus ergibt sich die Folge zu:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1.597, ….
Die Glieder der Fibonacci-Folge werden Fibonacci-Zahlen genannt.
Situationsbedingte Anwendungen, in denen ein Anfangswert Null keinen Sinn hat, werden
beginnend mit f1 = 1 und f2 = 1 definiert.
Eine Besonderheit der Fibonacci-Folge ist, dass das Quadrat von zwei aufeinander folgenden
Fibonacci-Zahlen immer auch eine Fibonacci-Zahl ergibt.
Als Beispiel sei hier das Quadrat der 5. + 6. Fibonacci-Zahl aufgeführt:
Fibonacci Zahl
Quadrat der Fibonacci Zahl
5
5
25
6
8
64
-te Zahl
Addition 5 + 6
Addition 25 + 64
11
89
__________________________________________________________________________________
2 Als Rekursion bezeichnet man die Technik in Mathematik, Logik und Informatik, eine Funktion durch sich
selbst zu definieren.
4
4.
Herleitung der Fibonacci-Folge
Leonardo Fibonacci führte die Fibonacci-Folge am Beispiel einer Kaninchenpopulation ein.
Dieses Kaninchenproblem ist in seinem „Buch der Rechenkunst“3 (siehe 2. Leonardo Fibonacci)
niedergeschrieben und lautet wie folgt:
Man geht davon aus, dass es ein Kaninchenpärchen („Elternpärchen“) in einem eingezäunten
Gebiet am 1. Januar eines Jahres gibt, welches ein weiteres (Kinder-) Kaninchenpärchen am
1. Februar und an jedem weiteren ersten Tag eines Monats wirft.
Ferner nimmt man an, dass jedes neue (Kinder-) Kaninchenpärchen einen Monat lang zur
Geschlechtsreife heranwächst, also selbst ein „Elternpärchen“ wird und dann selbst wiederum
im dritten Lebensmonat und an jedem weiteren ersten Tag eines Monats auch ein (Kinder-)
Kaninchenpärchen wirft.
Wie viele (Kinder- und Eltern) Kaninchenpärchen leben dann nach
Monaten, wenn zu
Beginn ein junges Paar lebte?
__________________________________________________________________________________
3 Liber abaci, das "Buch der Rechenkunst", erschien in der westlichen Welt, als die erste umfassende
Darstellung des neuen Rechensystems, basierend auf der indisch-arabischen Zahlenschreibung.
5
Den dazu notwendigen Wachstumsbestand nach einem Jahr
=13 kann man tabellarisch
darstellen:
Monate
Elternkaninchenpärchen Kinderkaninchenpärchen
Alle Kaninchenpärchen
1. Januar
1
0
1
1. Februar
1
1
2
1. März
2
1
3
1. April
3
2
5
1. Mai
5
3
8
1. Juni
8
5
13
1. Juli
13
8
21
1. August
21
13
34
1. September
34
21
55
1. Oktober
55
34
89
1. November
89
55
144
1. Dezember
144
89
233
1. Januar
233
144
377
(nächsten Jahres)
Schlussfolgerung:
Nach einem Jahr gäbe es 233 Elternkaninchenpärchen und 144 Kinderkaninchenpärchen, also
377 Kaninchenpärchen (754 Kaninchen) insgesamt.
Für die Beantwortung der Frage, wie viele Kaninchen nach
Monaten leben, muss man eine
allgemeine Vorschrift, also eine Folge finden, die die Berechnung jedes einzelnen Folgeglieds
ermöglicht: Wie bereits gesagt bildet sie jedes neue Folgeglied aus der Summe der beiden
vorherigen Glieder.
für
Dabei gilt für die Anfangsglieder
und
(siehe 2. Fibonacci-Folge).
Folgen mit dieser Rekursionsvorschrift werden allgemeine Fibonacci-Folgen genannt.
6
5.
Analogie zum Golden Schnitt
Der Goldene Schnitt ist ein bestimmtes Verhältnis zweier Zahlen oder Größen4. Weitere
verwendete Bezeichnungen sind stetige Teilung und göttliche Teilung.
Der Goldene Schnitt steht in enger Verbundenheit zur unendlichen Zahlenfolge der
Fibonacci-Zahlen:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1.597, ….
Berechnet man den Quotienten zweier aufeinanderfolgender Folgenglieder
man, dass sich dieser für große
so merkt
s, dem Wert 1,61803398 annähert. Dieser Wert wird auch
Goldener Schnitt genannt.
Das Verhältnis Φ zwischen der größeren und der kleineren Seite bezeichnet man als Goldene
Zahl. Sie hat den Wert
__________________________________________________________________________________
4 Größen werden mathematisch als reelle Vielfache einer Einheit dargestellt im Rahmen eines von einer Einheit
erzeugten reellen Vektorraums.
7
Hierzu die entsprechenden Quotienten aus den ersten 12 (bzw. 13) Fibonacci-Zahlen.
Nenner
Zähler
Verhältnis
Abweichung zu Φ in %
=1
=1
1,000000
-38,1966
=1
=2
2,000000
23,6068
=2
=3
1,500000
-7,2949
=3
=5
1,666667
3,00566
=5
=8
1,600000
-1,11456
=8
= 13
1,625000
0,43052
= 13
= 21
1,615385
-0,16374
= 21
= 34
1,619048
0,06265
= 34
= 55
1,617647
-0,02392
= 55
= 89
1,618182
0,00914
= 89
= 144
1,617977
-0,00349
= 144
= 233
1,618056
0,00133
Der Goldene Schnitt Φ ist eine irrationale Zahl. Sie lässt sich am leichtesten durch eben diese
Division zweier aufeinander folgender Fibonacci-Zahlen darstellen:
Dieser lässt sich auch als der unendliche Kettenbruch darstellen:
(Kettenbruchdarstellung5)
__________________________________________________________________________________
5 Ein Kettenbruch heißt einfach oder regulär (Der Kettenbruch heißt regulär, wenn in den Zählern immer eine 1
steht).
8
6.
Beispiele
Aus dem eben beschriebenen Zusammenhang zwischen dem Goldenem Schnitt und der
Fibonacci-Folge ergeben sich erstaunlich viele Beispiele für die Fibonacci-Folge in unserem
alltäglichen Leben.
Der Goldene Schnitt findet sich fast überall in den für uns als „richtige“, „normgerechte“
Proportionen wieder. Dabei stößt man auch oftmals auch auf unsere Fibonacci-Zahlen.
Die Fibonacci–Folge und eine Sonnenblume (Vorkommen in der Natur)
Die wohl spektakulärste exemplarische Realisierung für die des Goldenen Schnitts in der
Natur findet sich bei der Anordnung von pflanzlichen Blättern (Phyllotaxis6) wieder. Hierbei
teilt der Winkel zwischen zwei aufeinander folgenden besagten Blättern den Vollkreis von
360° in exakt dem Verhältnis des Goldenen Schnittes, wenn man die beiden Blattwurzeln
durch eine sogenannte Parallelverschiebung7 eines der Blätter entlang der Pflanzenachse zur
Deckung bringt. Es handelt sich um den Goldenen Winkel von etwa 137,5°.
Die bekanntesten Beispiele sind die Blütenblätter der Rose, Zapfen und die Kiefernnadel an
jungen Ästen.
Abb.: Blattstand einer Pflanze mit einem
Blattabstand nach dem Goldenen Winkel
__________________________________________________________________________________
6 Phyllotaxis ist die Lehre der Blattstellung von Pflanzen.
7 Die Parallelverschiebung ist eine geometrische Abbildung, die jeden Punkt der Zeichenebene oder des Raumes
in derselben Richtung um dieselbe Strecke verschiebt.
9
Die Sonnenblume als Beispiel
Jede einzelne Blüte der Sonnenblume bildet zwei Systeme von Spiralen, die vom Mittelpunkt
ausgehen. Es sind häufig 55 rechtsdrehende und 34 linksdrehende Spiralen. Unüblicher sind
dagegen. Arten mit 21 und 34 Spiralen. Die Riesensonnenblume hat 144 und 233 Spiralen.
Abb.: Sonnenblume
Abb.: Sonnenblume (Spiralmuster)
Blütenstände und Blattanordnung verlaufen oft in Spiralmustern, in sogenannten
Fibonacci-Spiralen.
Die Fibonacci-Zahlen sind fester Bestandteil unseres Lebens und wir können aus ihnen auf
unterschiedlichste Weise profitieren:
-
Beim Bau von Instrumenten spielen die Fibonacci-Zahlen und der Goldene Schnitt
eine tragende Rolle, sie sollen beispielsweise dem Resonanzkörper von
Streichinstrumenten besonderen Klang verleihen.
-
In der technischen Thematik werden die Proportionen des Goldenen Schnitts unter
anderem beim Papierformat (DIN A4), bei Fernsehbildern und bei Monitoren
eingesetzt.
-
Umstritten ist die Anwendung der Fibonacci-Zahlen im Börsengeschäft. Die
Fibonacci-Konjunkturzyklen sollen angeblich Schwankungen der Vergangenheit nicht
nur erklären, sondern die der Zukunft sogar vorhersagen können.
-
Die Fibonacci-Folge kann auch zur Verschlüsselung verwendet werden. In dieser
Funktion hat sie auch im Bestseller Sakrileg von Dan Brown8 ihr Debüt.
__________________________________________________________________________________
8 Sakrileg ist der Titel der 2004 erschienenen Übersetzung eines Thrillers von Dan Brown, der 2003 unter dem
Titel The Da Vinci Code erschien.
10
Abb.: Fibonacci-Spirale
7.
Nachwort
Content
11
8.
Literaturverzeichnis
Primärquellen:
Microsoft ® Encarta ® Enzyklopädie 2005
© 1993-2004
Microsoft Corporation
Internetquellen:
http://de.wikipedia.org/wiki/Leonardo_Fibonacci
http://de.wikipedia.org/wiki/Fibonacci-Folge
http://de.wikipedia.org/wiki/Der_Goldene_Schnitt
Bildquellen:
Leonardo Fibonacci
http://sv.wikipedia.org/wiki/Fil:Fibonacci2.jpg
Blattstand einer Pflanze mit einem Blattabstand nach dem Goldenen Winkel
http://de.wikipedia.org/w/index.php?title=Datei:Goldener_Schnitt_Blattstand.png
Sonnenblume
http://www.mathematik.tu-bs.de/FA-Workgroup/tsonar/VWProjekt/sblume.gif
Sonnenblume (Spiralmuster)
http://members.chello.at/gut.jutta.gerhard/sonnenbl.jpg
Fibonacci-Spirale
http://www.mahomathome.de/blog/wp-content/uploads/2009/05/fibonacci_spiral.png
Fußnoten:
http://de.wikipedia.org/wiki/Interdisziplinär
http://de.wikipedia.org/wiki/Rekursiv
http://www.ethbib.ethz.ch/exhibit/fibonacci/fibonacci-intro.html
http://de.wikipedia.org/wiki/Gr%C3%B6%C3%9Fe_(Mathematik)
http://delphi.zsg-rottenburg.de/kettenbruch.html
http://de.wikipedia.org/wiki/Phyllotaxis
http://de.wikipedia.org/wiki/Sakrileg_(Roman)
12
9.
Erklärung
Hiermit erkläre ich, dass ich die Arbeit ohne fremde Hilfe angefertigt und nur die im
Literaturverzeichnis angeführten Quellen und Hilfsmittel benutzt habe.
Wörtliche Zitate und sinngemäße Wiedergaben habe ich als solche kenntlich gemacht.
Mir ist bekannt, dass bei einem Verstoß gegen diese Regeln meine Arbeit mit 0 Punkten
bewertet wird.
01.07.2009
_________________________________________________________
Ort, Datum
Unterschrift
13