Zellmembrane
Werbung

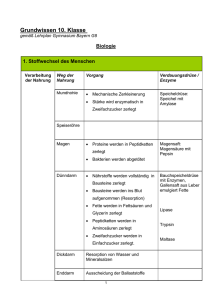
Zellmembrane Natalie Emken Seminar DGL in der Biomedizin, SS 09 27. Mai 2009 Gliederung 1. 2. 3. 4. 5. 6. 7. 8. 9. Die Zellmembran Diffusion Erleichterte Diffusion Carrier-vermittelter Transport Aktiver Transport Das Membranpotential Osmose Kontrolle des Zellvolumens Quellenangaben 1. Die Zellmembran Die Zellmembran umgibt die lebende Zelle und begrenzt deren inneren Vorgänge von der äußeren Umgebung Die Austauschvorgänge zw. der Zelle und ihrer Umgebung spielen sich an der äußeren Zellhülle, der Zellmembran ab Die Zellmembran ist selektiv permeabel: Selektiv werden verschiedene Stoffe durchgelassen oder aufgehalten Sie ist dadurch zugleich Trennwand und Träger vieler Stoffwechselprodukte 1. Die Zellmembran 1.1 Aufbau Abb. 1: Schematische Darstellung einer Zellmembran (Quelle: http://www.was-ist-q10.de/images/aerzte_10_01.GIF) 1. Die Zellmembran 1.2 Aufgaben der Membranproteine Die Plasmamembran und die Membran verschiedener Organellen verfügen jeweils über eine charakteristische Proteinausstattung Sie wirken als Träger- und Transportmoleküle Sie durchbrechen die wasserunlösliche Lipidschicht und schaffen dadurch Poren und Kanäle Sie beteiligen sich am Stoffwechsel der Zelle Sie tragen zur Festigkeit der Membran bei 1. Die Zellmembran 1.3 Transportmechanismen Vernachlässigt man zunächst die Frage der Energieabhängigkeit, so lassen sich konzeptionell drei Transporttypen unterscheiden ◦ Uniport ◦ Antiport ◦ Symport Man unterscheidet dabei jedoch zwischen aktiven und passiven Transportprozessen 1. Die Zellmembran 1.3 Transportmechanismen Passive Transportmechanismen sind: ◦ ◦ ◦ ◦ Einfache Diffusion Erleichterte Diffusion Carrier-vermittelter Transport Osmose Aktive Transportmechanismen sind: ◦ Ionenpumpen, bei denen unter Hydrolyse von ATP zu ADP bestimmte Ionen entgegen ihren jeweiligen Konzentrationsgradienten transportiert werden ◦ Z.B. die Natrium-Kalium-ATPase und die Calcium-ATPase 2. Diffusion Sei u die Menge eines chemischen Stoffes, Ω sei ein Teil des Raumes. Dann gilt: d ◦ ◦ ◦ ◦ u dV f dV J n dA dt ∂Ω ist der Rand von Ω n ist die reguläre äußere Einheit zu ∂Ω f ist die lokale Produktion von u pro m³ J ist der Fluss von u Falls J ausreichend glatt ist, gilt J n dA J dV Falls die Größe in der u gemessen ist, fest aber beliebig ist, gilt der folgende Erhaltungssatz u t f J 2. Diffusion 2.1 Ficksches Gesetz Die einfachste Beschreibung für den Fluss chemischer Stoffe ist J Du (Ficksches Gesetz) Wenn das Ficksche Gesetz gilt wird der Erhaltungssatz zur Reaktions-Diffusionsgleichung u Du f t Falls D konstant ist, so folgt weiter u D² u f t 2. Diffusion 2.2 Diffusionskoeffizienten Für große kugelförmige gelöste Moleküle gilt D ◦ ◦ ◦ ◦ k ist die Boltzmann-Konstante T ist die absolute Temperatur der Lösung µ ist die Viskosität der Lösung a ist der Radius des gelösten Moleküls kT D Für nichtkugelförmige Moleküle gilt f ◦ f ist der Funktionalkoeffizient von Stokes der Teilchen Mit der Molekularmasse und Molekulardichte 4 M a³ 3 kT D 3 6 ² M 1/ 3 kT 6a 2. Diffusion 2.3 Diffusion durch eine Membran Annahme: Die Membran (mit Dicke L) grenzt zwei große Bereiche einer verdünnten Chemikalie ab cl= Konzentration im linken Bereich (bei x=0) cr= Konzentration im rechten Bereich (bei x=L) Entsprechend zur Diffusionsgleichung gilt c ² c D t x² in Abhängigkeit von den Randbedingungen c(0,t)= cl , c(L,t)= cr 2. Diffusion 2.3 Diffusion durch eine Membran c 0, Im stabilen Zustand, t J ² c D 0 folgt dass x x² J ist konstant oder c( x ) ax b x Wir erhalten also c( x ) cr cl cl Der Fluss von Chemikalien ist konstant L D J cl cr L 3. Erleichterte Diffusion Bei der erleichterten Diffusion spielen die zwei Faktoren Diffusion und Reaktion eine Rolle Sie ereignet sich, wenn der Fluss einer Chemikalie durch eine Reaktion, die im diffusen Medium stattfindet, verstärkt wird Beispiel: Fluss von Sauerstoff in Muskelfasern (der Sauerstoff ist an Myoglobin gebunden und wird als Oxymyoglobin transportiert) 3. Erleichterte Diffusion 3.1 Erleichterte Diffusion von Sauerstoff Annahme: Wir haben einen „Slab reactor“, welcher diffundierendes Myoglobin enthält Die Sauerstoffkonzentration links (bei x=0) wird bei s0 und rechts (bei x=L) bei sL gehalten (s0>sL) Falls f die Aufnahmerate von Sauerstoff in Oxymyoglobin beschreibt, dann gelten s ² s Ds f (1) f k c k se folgt t x² aus der Reaktionsgleichung k+ e ² e O + Mb MbO2, 2 De f (2) kt x² s O , e Mb , c MbO c ² c Dc f (3) t x² 2 2 3. Erleichterte Diffusion 3.1 Erleichterte Diffusion von Sauerstoff Es ist sinnvoll De=Dc zu setzen, da Myoglobin und Oxymyoglobin nahezu identisch in Molekularmasse und –struktur sind Es ist außerdem sinnvoll die Randbedingungen zu spezifizieren, da das Myoglobin und das Oxymyoglobin in dem „Slab“ bleiben e c 0 bei x 0 und x L x x Die totale Menge des Myoglobin bleibt außerdem bei der Reaktion am stationären Zustand erhalten (e+c=e0), so dass (2) überflüssig ist und 0 st ct Ds sxx Dc cxx 3. Erleichterte Diffusion 3.1 Erleichterte Diffusion von Sauerstoff Integration von 0 st ct Ds sxx Dc cxx bzgl. x liefert ds dc Ds Dc J dx dx J ist die Summe aus dem Fluss des freien Sauerstoff und dem des gebundenen und bildet damit den Fluss des totalen Sauerstoffs Durch erneute Integration bzgl. x=0 und x=L können wir J bzgl. der Grenzwerte beider Konzentrationen ausdrücken Ds Dc J ( s0 sL ) ( c0 cL ) L L 3. Erleichterte Diffusion 3.1 Erleichterte Diffusion von Sauerstoff Durch die dimensionslosen Variablen k c s , u und x Ly k e0 erhalten wir aus (1) und (3) die Gleichung e1 yy 1 u u e2 yy , Ds Dc wobei e1 und e2 e0kL² kL² Mit diesen Zahlen können wir e1 und e2 abschätzen, welche sehr klein sind und darauf hinweisen, dass für Sauerstoff und Myoglobin im gesamten Medium gilt es k c 0 mit K Ks k 3. Erleichterte Diffusion 3.1 Erleichterte Diffusion von Sauerstoff Durch Substitution in die Gleichung für den gesamten Fluss J erhalten wir nun Ds Dc so sL J so sL e0 L L K so K sL Dc Ds e0K so sL 1 L Ds so K sL K Ds 1 s0 sL , L D e K² wobei c o und so K sL K Ds K Bei Anwesenheit von Trägerstoffen ist die Diffusion durch den Faktor verstärkt 3. Erleichterte Diffusion 3.2 Erleichterte Diffusion bei der Muskelatmung Um ein Membranpotential aufrecht zu erhalten, wird ATP konstant verbraucht Dieser Verbrauch von Energie erfordert die konstante Umwandlung von Zucker Dabei verbrauchen die Muskelfasern Sauerstoff Zucker kann zwar auch anaerob umgewandelt werden, jedoch wirkt das dadurch entstehende Abfallprodukt (Milchsäure) toxisch Aus diesem Grund muss der Sauerstoff vom Äußeren der Zelle zum Zentrum der Zelle vordringen, um Sauerstoffschuld zu verhindern 3. Erleichterte Diffusion 3.2 Erleichterte Diffusion bei der Muskelatmung Um zu erklären wie das Myoglobin die Versorgung einer Muskelzelle mit Sauerstoff fördert und dabei hilft Sauerstoffschuld zu verhindern, untersuchen wir ein Modell des Sauerstoffverbrauch Es berücksichtigt den Effekt der Sauerstoffdiffusion und der Myoglobindiffusion Annahmen: ◦ Eine Muskelfaser ist ein langer kreisförmiger Zylinder (mit Radius a=2,5x10-³cm) ◦ Diffusion findet nur in radialer Richtung statt ◦ Die Sauerstoffkonzentration am Rand ist fest und konstant ◦ Die Verteilung chem. Stoffe verläuft polysymmetrisch 3. Erleichterte Diffusion 3.2 Erleichterte Diffusion bei der Muskelatmung Mit diesen Annahmen sind die stationären Zustandsgleichungen, die die Diffusion von Sauerstoff und Oxymyoglobin beschreiben, gegeben durch 1 d ds Ds r f g 0 r dr dr 1 d dc Dc r f 0 r dr dr Der neue Ausdruck g beschreibt den konstanten Sauerstoffverbrauch und die Randbedingungen sind dc ds dc s sa , 0 bei r a und 0 bei r 0 dr dr dr 3. Erleichterte Diffusion 3.2 Erleichterte Diffusion bei der Muskelatmung k mit e1 c Durch dimensionslose Variablen, s , u und r ay k e0 erhalten wir 1 d d 1 d du e1 y 1 u u e y 2 y dy dy y dy dy Ds Dc g , e2 und e0k a² ka² k Hieraus folgt außerdem, dass 1 d d 1 d du e1 y e2 y y dy dy y dy dy 3. Erleichterte Diffusion 3.2 Erleichterte Diffusion bei der Muskelatmung Durch zweimalige Integration bzgl. y erhalten wir e1 e2u A ln y B y² 4 Hierbei sind A und B durch die Randbedingungen bestimmt Geringe Sauerstoffschuld tritt ein, falls σ=u=0 bei y=0 Für diese Grenzwerte setzen wir A=B=0 Die Konzentration am Rand muss dann mindestens so groß wie σ0 sein, wobei wir den quasi Steady-state 1 benutzt haben 1 u u 1 u 1 0 e2 0 , mit 0 1 4e1 e1 3. Erleichterte Diffusion 3.2 Erleichterte Diffusion bei der Muskelatmung Abb. 2: Funktion der Kritischen Sauerstoffkonzentration, abhängig von dem Sauerstoffverbrauch (Quelle: KEENER J. & J. SNEYD (2001): Mathematical Physiology, S.44) 4. Carrier-vermittelter Transport Manche Substanzen sind in der Zellmembran unlöslich, durchströmen sie aber dennoch Carriervermittelter Transport Carrier sind auf ganz bestimmte Moleküle spezialisiert (ähnlich wie Enzyme), für die sie eine Bindungsstelle besitzen Jeder zu transportierende Stoff ist auf sein entsprechendes Carrier-Protein angewiesen Es gibt 3 Typen von Trägervermittelten Transport ◦ Uniport ◦ Symport ◦ Antiport 4. Carrier-vermittelter Transport 4.1 Glucosetransport Tritt auf, wenn die Bindungsstellen des Trägermoleküls abwechselnd von der extrazellulären Seite und der intrazellulären Seite der Membran zugänglich sind Bei diesem Prozess handelt es sich um einen Uniport Abb. 3: Glucosetransport in der Zellmembran (Quelle: http://www.biochem.arizona.edu/classes/bioc462/462 a/NOTES/LIPIDS/Fig12_27ModelGluT1transpt.GIF (abgerufen am. 10.05.2009)) 4. Carrier-vermittelter Transport 4.1 Glucosetransport Wir können den Prozess des Glucosetransport folgendermaßen formulieren: Annahmen: ◦ Die Population des Enzym-Trägerproteins C hat zwei konformative Stadien Ci und Ce ◦ Das Glukose-Substrat Si an dem Inneren kann mit dem Enzym Ci gebunden sein, um den Komplex Pi zu formen ◦ Das Glukose-Substrat Se an dem Äußeren kann mit dem Enzym Ci gebunden sein, um den Komplex Pe zu formen Si + C i k k Pi Ci k k k Pe Ce k k Se + C e 4. Carrier-vermittelter Transport 4.1 Glucosetransport Die DGL sind gegeben durch dsi k pi k si ci J dt dse k pe k sece J dt dpi kpe kpi k si ci k pi dt dpe kpi kpe k sece k pe dt dci kce kci k pi k sici dt dc e kci kce k pe k sece dt (4.1) (4.2) (4.3) (4.4) (4.5) (4.6) 4. Carrier-vermittelter Transport 4.1 Glucosetransport Zwei Degenerationen: ◦ Der totale Betrag vom Rezeptor bleibt erhalten und daher gilt pi pe ci ce c0 ◦ Der totale Betrag von Glucose bleibt erhalten und daher gilt si se pi pe const . Zusammen mit den Gleichungen (4.1-4.6) am stationären Zustand bilden sie ein lineares System für die fünf Unbekannten pi , pe , ci , ce und J 4. Carrier-vermittelter Transport 4.1 Glukosetransport Wir können also J berechnen und es gilt 1 se si J K d Kk C0 , si K Kd se K Kd Kd ² 2 wobei K k k und K d k k Für den dimensionslosen Fluss gilt dann e i j , i 1 e 1 ² wobei i si K , e se K und K d K 4. Carrier-vermittelter Transport 4.2 Symport und Antiport Modelle für Symport und Antiport folgen in ähnlicher Weise Das Trägerprotein besitzt in diesem Fall mehrere Bindungsstellen, welche zum intrazellulärem und extrazellulärem Raum ausgerichtet sein können Ein Austausch der Konstellation tauscht die Lage aller beteiligten Bindungsstellen vom Inneren zum Äußeren oder anders herum Ein Beispiel für einen Antiport ist der Natrium-CalciumAustauscher in Muskeln- und Nervenzellen Ein Beispiel für einen Symport ist der natriumangetriebene Glukose-Symporter 4. Carrier-vermittelter Transport 4.2 Symport und Antiport Falls es k Bindungsstellen gibt, die am Austausch beteiligt sind, so gibt es 2k mögliche Kombinationen von gebundenen und ungebundenen Seiten Schlüsselannahme für das Modell: Es ist nur der vollständig gebundene oder vollständig ungebundene Träger an einem konformativen Austausch beteiligt Abb. 4: Stadien und mögliche Übergänge eines Transporters mit zwei Substraten S und T und einer Bindungsstelle für jedes (Quelle: KEENER J. & J. SNEYD (2001): Mathematical Physiology, S.47) 4. Carrier-vermittelter Transport 4.2 Symport und Antiport Wir ignorieren im folgenden die Zwischenprodukte, da die Analysis dieses völlig allg. Reaktionsschemas kompliziert ist Das Reaktionsschema vereinfacht sich dann zu k mS + nT + C P k Die Ergebnisse für einen Symport und einen Antiport sind jetzt ähnlich dem des Uniport 4. Carrier-vermittelter Transport 4.2 Symport und Antiport Für den Fluss des Symport erhalten wir semt en simt in 1 J K d Kk C 0 m n si ti K Kd semten K Kd Kd ² 2 wobei der Fluss von s mJ und der Fluss von t nJ ist und kc kc kp kp k und K k / k und Kd k / k Für den Fluss des Antiport erhalten wir 1 semtin simten J Kd Kk C0 m n si te K Kd semtin K Kd Kd ² 2 5. Aktiver Transport Der oben beschriebene trägervermittelte Transport erfolgt immer unter elektrochemischen Gradienten und ist somit durch Diffusion gekennzeichnet Viele Prozesse, die gegen Gradienten arbeiten, beanspruchen einen Energieaufwand Als wichtigstes Beispiel für den aktiven Transport dient die Natrium-Kalium-Pumpe Sie reguliert das Zellvolumen und hält ein Membranpotential aufrecht Der Antrieb dieser Pumpe verbraucht allerdings meistens einen Drittel des Energiebedarfs 5. Aktiver Transport 5.1 Die Natrium-Kalium-Pumpe Die Natrium-Kalium-ATPase ist ein in der Zellmembran verankertes Transmembranprotein Das Enzym katalysiert unter Hydrolyse von ATP den Transport von Natrium-Ionen aus der Zelle und den Transport von Kalium-Ionen in die Zelle gegen den Konzentrationsgradienten Je Molekül ATP werden 3 Natrium-Ionen aus der Zelle und 2 Kalium-Ionen in die Zelle befördert Die Pumpaktivität dieser Pumpe nutzt Energie bei der Dephosphorylation von ATP in ADP durch das allgemeine Reaktionsschema ATP + 3Nai+ + 2Ke+ ADP + Pi + 3Nae+ + 2Ki+ 5. Aktiver Transport 5.1 Die Natrium-Kalium-Pumpe Abb. 5: Na+-K+-ATPase (Quelle: http://www.bioc.uzh.ch/bipweb/lexikon/proteine/nakatpase/nakatpase.gif (abgerufen am 16.05.2009)) 5. Aktiver Transport 5.1 Die Natrium-Kalium-Pumpe Zur Umwandlung in ein mathematisches Modell, ziehen wir ein vereinfachtes Modell in Betracht Es existiert demnach nur eine einzige Bindungsstelle für Natrium und Kalium Eins-zu-eins Austausch Wir bezeichnen das Trägermolekül mit C und nehmen folgende Reaktionen an Nai+ + C NaC NaCP Na e+ + CP ATP CP + Ke+ ADP KCP KC P + KC Ki+ + C 5. Aktiver Transport 5.1 Die Natrium-Kalium-Pumpe Wir setzen auf diese das Massenwirkungsgesetz an J beschreibt wieder die Rate mit der das Natrium und Kalium bereit steht bzw. beseitigt wird Der Fluss von Ionen durch die Pumpe im stationären Zustand ist dann gegeben durch J C0 Na K K K Na K K K P K K K K K Na K Na K K e i 2 i e i 1 2 2 n i e 1 1 2 e 1 wobei K1 k1k2kp , K 1 k1k2k p , K 2 k3k4k5 , K 2 k3k4k5 , Kn k1kp k2k1 k2kp und Kk k3k4 P k3k5 k4k5 , k 5. Aktiver Transport 5.1 Die Natrium-Kalium-Pumpe Da ATP viel dynamischer ist als ADP, erwarten wir, dass die rückwärts gerichtete Reaktionsrate k-p im Vergleich zur vorwärts gerichteten Reaktionsrate gering ist Falls wir also die entgegengesetzte Reaktion ignorieren (K-1=0), erhalten wir J C0K1K 2 Na K K K K K K Na K K e 2 i i e 2 n i , 1 k Diese Gleichung ist unabhängig von der extrazellulären Natrium-Konzentration 5. Aktiver Transport 5.2 Die Calcium-ATPase Andere wichtige Pumpen sind die Ca2+-ATPase und Transporter, die die intrazelluläre Ca2+-Konzentration gering halten Inneres freies Calcium wird bei geringen Konzentrationen, gegenüber den hohen extrazellulären Calciumkonzentrationen, aufrecht erhalten Man geht davon aus, dass viele Signalwege über eine feine Regulation der örtlichen Calciumkonzentration gesteuert werden Die am besten zu verstehende Ca2+ Pumpe ist eine ATPase in dem sarkoplasmatischen Retikulum der Muskelzellen 6. Das Membranpotential Zwischen Außen- und Innenseite der Membran besteht bei allen Zellen eine elektrische Spannung das Membranpotential Da das Cytoplasma einer Zelle im Vergleich zur extrazellulären Flüssigkeit negativ geladen ist, begünstigt das Membranpotential den passiven Transport von Kationen in die Zelle hinein und von Anionen aus ihr heraus Dadurch treiben zwei Kräfte die Diffusion an, das chemische Konzentrationsgefälle und das elektrische Membranpotential der elektrochemische Gradient 6. Das Membranpotential Das Membranpotential ist eine Konsequenz der oben beschriebenen aktiven Transportprozesse, die Ionen aktiv transportieren Z.B. der Ablauf der Natrium-Kalium-Pumpe führt dazu, dass mit jeder „Umdrehung“ insgesamt eine positive Ladung aus dem Cytoplasma in die extrazelluläre Flüssigkeit verschoben wird Wir definieren den Potentialunterschied durch die Zelle als V=Vi-Ve 6. Das Membranpotential 6.1 Das Nernst-Gleichgewichtspotential Die Nernst-Gleichung ist eine der wichtigsten Gleichungen in der Elektrophysiologie Sie gestattet die Berechnung der Spannungsänderung in Abhängigkeit von der Konzentrationsänderung der beteiligten Ionen Mit der Nernst-Gleichung lässt sich die Gleichgewichtslage dieses Vorgangs beschreiben 6. Das Membranpotential 6.1 Das Nernst-Gleichgewichtspotential Modellierung: Inneres S i S' i Vi Zellmembran, permeabel für S, aber nicht S‘ Äußeres S S S e S' e Ve Die Diffusion von S bewirkt einen Ladungsaufbau Dieses Ladungsungleichgewicht baut abwechselnd ein elektrisches Kraftfeld auf Dies setzt sich der weiteren Diffusion von S entgegen Ein Gleichgewicht stellt sich ein, wenn das Kraftfeld exakt die Diffusion von S ausgeglichen hat 6. Das Membranpotential 6.1 Das Nernst-Gleichgewichtspotential Das Gleichgewichtspotential Vs eines Ions ist durch das Nernst-Potential gegeben RT S e kT S e ln Vs ln zF S i zq S i ◦ ◦ ◦ ◦ ◦ R ist die allgemeine Gaskonstante T ist die absolute Temperatur F ist die Faraday-Konstante k ist die Boltzmann-Konstante q ist die Landung von dem Ion S R Eine besonders wichtige Beziehung ist k Na ◦ N ist die Avogadro-Zahl a 6. Das Membranpotential 6.1 Das Nernst-Gleichgewichtspotential Herleitung der Nernst-Gleichung: Wie bereits beschrieben, wird der Fluss durch den elektrochemischen Gradienten angetrieben Der Beitrag zu dem Fluss durch das Kraftfeld ist durch Plancks Gleichung gegeben z J u c z ◦ ◦ ◦ ◦ ◦ u ist die Beweglichkeit des Ions z ist die Ladungszahl des Ions c ist die Konzentration von S Ф ist das elektrische Potential → beschreibt das Kraftfeld 6. Das Membranpotential 6.1 Das Nernst-Gleichgewichtspotential Es gibt eine Beziehung zwischen der Ionenmobilität u RT und der Fickschen Diffusionskonstante Du zF Durch Kombination mit dem Fickschen Gesetz erhalten wir die Nernst-Planck-Gleichung zF J D c c RT Falls der Ionenfluss und das Kraftfeld quer zur Membran verlaufen, können wir die obige Gleichung als die eindim. Relation dc zF d betrachten J D c dx RT dx 6. Das Membranpotential 6.1 Das Nernst-Gleichgewichtspotential Für den Gleichgewichtszustand, d.h. wenn kein Nettostrom fließt, muss gelten dc zF d 0 D c dx RT dx 1 dc zF d 0 c dx RT dx Integration von x=0 bis x=L liefert dann lnc ce ci zF i e RT Und mit V=Фi-Фe können wir schließlich aus der NernstPlanck-Gleichung die Nernst-Gleichung ableiten 6. Das Membranpotential 6.2 Die Goldman-Hodgkin-Katz (GHK)-Gleichung Eigentlich bestimmt die lokale Ladungsdichte das elektrische Potential Ф, so dass J durch ein gekoppeltes System von Gleichungen bestimmt werden muss Ein nützliches Resultat erhalten wir jedoch, falls das Kraftfeld als konstant angenommen wird Für einen Potentialunterschied V= Ф(0)-Ф(L) in einer Membran mit Dicke L und den Konzentrationen links [S]=ci und rechts[S]=ce erhalten wir V x L Und durch Einsetzen in die Nernst-Planck-Gleichung folgt dc zFVc J dc zF d J D c 0 dx RTL D dx RT dx 6. Das Membranpotential 6.2 Die Goldman-Hodgkin-Katz (GHK)-Gleichung Die Lösung dieser gewöhnlichen DGL mit den Randbedingungen c(0)=ci und c(L)=ce ist gegeben durch JRTL zVFx zVFx exp c x 1 c i exp RTL DzVF zFV c i ceexp D zFV RT J L RT zFV 1 exp RT RTL Durch Multiplikation mit zF wird diese Flussdichte zur elektrischen Stromdichte und wir erhalten die GHKStrömungsgleichung zFV D PS ist die L Permeabili tät c i ce exp z² F ² RT IS PS V RT zFV 1 exp RT 6. Das Membranpotential 6.2 Die Goldman-Hodgkin-Katz (GHK)-Gleichung Für eine Ansammlung von Ionen, alle mit Ladungszahl z=±1, können wir das GHK-Potential direkt berechnen Falls die elektrochemische Triebkraft Null ist, gilt VF VF j j cij cej exp c c exp i e Dj RT RT 0 Pj Pj mit Pj L VF VF z 1 z 1 1 exp 1 exp RT RT Dieser Ausdruck kann nach V aufgelöst werden, so dass j j für das GHK-Potential gilt RT z 1 Pj ce z 1 Pj ci V Beispiel: ln F z 1 Pj cij z 1 Pj cej RT PNa Na i PK K i PCl Cl e Vr ln F PNa Na e PK K e PCl Cl i 6. Das Membranpotential 6.2 Die Goldman-Hodgkin-Katz (GHK)-Gleichung Der Membranstrom IS kann auch durch die sogenannte elektrochemische Triebkraft V-VS ausgedrückt werden IS=g(V-VS) (g=1/r ist die Membranleitfähigkeit) Wenn diese Null ist, wird die zufällige Ionenbewegung, die zu einer Ausgleichung der Ionenkonzentrationen auf beiden Seiten der Zellmembran führen würde, durch eine elektrische Potentialdifferenz ausgeglichen Die Summe aller Ionenströme ist dann Null 7. Osmose Osmose ist passiver Transport von Wassermolekülen P2 Modellierung: P1 Kammer 2 Kammer 1 Q H2O Semipermeable Membran Eine lineare Beziehung zwischen dem Druckunterschied und dem Fluss von Wasser durch eine Membran ist gegeben durch rQ P1 P2 ◦ Q ist der Fluss des Wassers von Kammer 1 in Kammer 2 ◦ P1 und P2 sind der entsprechende Druck ◦ r ist der Flusswiderstand der Membran 7. Osmose Durch Hinzufügen eines gelösten Stoffes in die 1. Kammer wir der effektive Druck der Lösung gesenkt Falls πs dieser effektive Druck ist, ist die Flussrate des gelösten Stoffes geändert und es gilt rQ P1 s P2 wobei πs=kcT der osmotische Druck ist ◦ k ist die Boltzmann-Konstante ◦ c ist die Konzentration des gelösten Stoffes (Moleküle pro VE) ◦ T ist die absolute Temperatur (πs=RcT, falls c in Mol pro VE ausgedrückt ist) Der Fluss von Wasser infolge des osmotischen Drucks wird Osmose genannt 7. Osmose Falls P1=P2, saugt der Effekt des osmotischen Drucks Wasser in die 1.Kammer und bewirkt eine Zunahme ihres Volumens Der Osmotische Druck wird durch die Anzahl von Partikeln pro VE des Fluids ermittelt und nicht durch die Masse der Partikel Konzentrierte Lösung Semipermeable Membran verdünnte Lösung H2O H2O Osmotischer Druck πs 8. Kontrolle des Zellvolumens Die Konzentrationsunterschiede, die durch ionische Pumpen aufgebaut und aufrecht erhalten werden, sind notwendig für die Zelle, um ihr Volumen zu kontrollieren Eine Zelle ohne starre Zellwand ist unfähig irgendwelchen hydrostatischen Druckunterschieden zu wiederstehen Eine hohe intrazelluläre Konzentration an Ionen und großen Molekülen kann also dazu führen, dass zu viel Wasser in die Zelle eintritt und sie anschwillt und platzt 8. Kontrolle des Zellvolumens Abb. 6: Schematische Darstellung eines „Pump-Leak Modells“ (Quelle: KEENER J. & J. SNEYD (2001): Mathematical Physiology, S.60) 8. Kontrolle des Zellvolumens Zusammen mit den aktiven Strömungen der NatriumKalium-Pumpe ergeben sich die Gleichungen RT Na e 3pq INa gNa V ln F Na i RT K e IK gK V ln 2pq F K i RT Cl e ICl gCl V ln F Cl i -p ist die Rate bei der die Ionenaustauschpumpe arbeitet -q ist die Ladung von einem einzigen Ion - X ist die Anzahl von Großen negativ geladenen Molekülen (mit Ladungszahl ≤-1) welche in der Zelle eingeschlossen sind - w ist das Zellvolumen Der osmotische Druck ist gegeben durch dw X r RT Na i Na e K i K e Cl i Cl e dt w 8. Kontrolle des Zellvolumens Wir können diese Strom-Spannungs-Gleichungen als DGL ausdrücken d RT Na e 3pq zqw Na i gNa V ln (1) dt F Na i d RT K 2pq zqw K g V ln dt F K d RT Cl zqw Cl g V ln dt F Cl i K e (2) i i Cl e i d I A zqw A z dt (3) 8. Kontrolle des Zellvolumens Bevor wir dieses System von Gleichungen analysieren, ist es nützlich ein paar physikalische Beobachtungen machen Die extrazellulären und intrazellulären Medien befinden sich nahezu in Elektroneutralität Nur nahe der Membran ist diese Elektroneutralität leicht gestört Diese Störung ist jedoch so gering, dass sie hier vernachlässigt werden kann und es gilt (4) Na e K e Cl e 0 und X Na i K i Cl i z x 0 w (5) 8. Kontrolle des Zellvolumens Um diese Gleichungen besser zu verstehen führen wir erneut dimensionslose Variablen ein qV pFq w ,P , Cl e und setzen y e RT RTgNa X Na Na i e e 3P K y, K i e e 2 P Cl y, Cl i e 1 y Die Gleichungen zur Elektroneutralität und des osmotischen Drucks werden dann zu 1 z 1 1 (1) y x 0 und (2) y 2 0, y y Na e K e Na K 3P e e e e 2 P , gNa gK 8. Kontrolle des Zellvolumens Für die eindeutige positive Nullstelle von (1) ergibt sich z z² 4 y in(2) 41 - ² 4 1 z x ² 0 2 Für zx≤-1 hat diese quadratische Gleichung eine positive Nullstelle, falls α<1 ist, d.h. Na e K e P Na K 3P e e e 2 P 1 e 3 Na Dies ist genau der Fall, wenn gilt gNa e 2 K gK e 8. Kontrolle des Zellvolumens Abb. 7: Funktion des Zellvolumen, abhängig von der Pumprate (Quelle: KEENER J. & J. SNEYD (2001): Mathematical Physiology, S.64) Abb. 8: Funktionen des Membranpotential und des Natrium- und Kalium-Gleichgewichtspotential, abhängig von der Pumprate (Quelle: KEENER J. & J. SNEYD (2001): Mathematical Physiology, S.64) 8. Kontrolle des Zellvolumens Hier ist die Pumprate als P=ρu³ dargestellt, wobei Na i u Na e Abb. 9: Funktionen des Membranpotential und des Natrium- und Kalium-Gleichgewichtspotential, abhängig von der Pumprate (Quelle: KEENER J. & J. SNEYD (2001): Mathematical Physiology, S.66) 9. Quellenangaben BIRBAUMER N. & R. F. SCHMIDT (2003): Biologische Psychologie, Berlin. HELMICH U. (2007): Arbeitsweise der Natrium-Kalium-Pumpe, online unter: http://www.u-helmich.de/bio/neu/1/11/112/vertiefung/vert01.html (abgerufen am 17.05.2009) KEENER J. & J. SNEYD (2001): Mathematical Physiology, Pasadena. LÖFFLER, HEINRICH & PETRIDES (2006): Biochemie und Pathobiochemie. UNIVERSITÄT STUTTGART (o.J.): Transport durch Membranen, online unter: http://www.unistuttgart.de/bio/bioinst/biophysik/lehre/skripte/biophysik_der_zelle/pdf/ kapitel_10.pdf (abgerufen am 17.05.2009) (o.A) (o.J):Transport, online unter: http://www.lrzmuenchen.de/~jmd/transport.htm (abgerufen am 20.05.2009)