Trägheitsmomente einiger Körper

Trägheitsmomente einiger
Körper
Im folgenden sind die Trägheitsmomente einiger häufig auftretender Körper einmal
explizit ausgerechnet. Dabei kommen immer Achsen um den Schwerpunkt zu tragen.
Es sei daran erinnert, dass bei Achsen parallel zu den hier berechneten leicht der Satz
von Steiner benutzt werden kann. Die allgemeine Ausgangsform der Berechnungen
ist die Definition des Trägheitsmomentes:
ZZZ
Z
2
J=
r| {z
r2 %(r)dV
dm} =
dm=ρ(r)dV
V
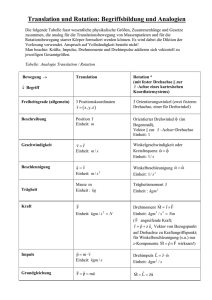
Ich möchte darauf hinweisen, dass die Bezeichnung r“ für den Abstand eines Mas”
Abbildung 1: Zum Trägheitsmoment
senpunktes von der Drehachse steht und zu Verwechslungen einlädt! Ein Fehler der
mich selbst schon eine dreiviertel Stunde Rechnung im Fall der Kugel gekostet hat!
Da die Dichte aller Körper als homogen angenommen wird (%(r) = const.), bedeutet
das:
ZZZ
J =%
r2 dV
V
Das Problem ist also nur noch“ das Auswerten des Integrals...
”
1
1 Quader
"Z
J
c
2
b
2
Z
Z
#
a
2
2
= %·
2
x +y
− 2c
"Z
c
2
− 2b
b
2
Z
Z
a
2
2
x
"
− 2b
Z
a
2
= % · bc ·
dxdydz
−a
2
= %·
− 2c
Z
c
2
Z
Z
b
2
x dx + ac ·
#
a
2
y
− 2c
−a
2
b
2
dxdydz +
−a
2
2
Z
− 2b
2
dxdydz
−a
2
#
2
y dy
− 2b
1
m 1
abc a2 + b2 =
· abc a2 + b2
12
abc 12
1
m a2 + b2
12
= %·
=
2 Kreiszylinder
Natürlich ist es angebracht Zylinderkoordinaten zu verwenden!
Z h Z 2π Z R
J = %·
r2 · rdrdϕdz
0
0
0
m
1
1
· 2πh · R4
= % · 2πh · R4 =
4
πR2 h
4
1
=
mR2
2
3 Kreiskegel
Wie sich aus der Geometrie ergibt, ist auch hier die Verwendung von Zylinderkoordinaten ratsam. Der Abstand von der Drehachse kann weiter mit r bezeichnet werden,
2
jedoch ist auf die Integrationsgrenzen und damit auch -reihenfolge zu achten!
Z
J
h
Z
2π
Z
= %·
0
0
R
hz
r2 · rdrdϕdz
0
Z
πR4 h 4
z dz
= %·
2h4 0
πR4 h
πR4 h
m
= %·
= π 2 ·
10
10
3R h
3
=
mR2
10
4 Kugel
Bei der Kugel kommt der oben gemachte Kommentar zu tragen, dass das r2“ in
”
der Def. des Trägheitsmomentes nicht unbedingt mit dem r“ aus dem gewählten, oft
”
krummlinigen Koordinatensystem zusammenfallen muss. Aus diesem Grund nennen
wir den Abstand von der Drehachse zunächst a und überlegen uns dann, wie dieser in
Kugelkoordinaten parametrisiert wird.
ZZZ
J = %·
a2 r2 sin ϑdrdϑdϕ
V
Wenn man die Drehachse durch die z-Achse legt gibt r in Kugelkoordinaten den Abstand von Koordinatenursprung und Massenpunkt an, wir wollen aber den Abstand a
zwischen z-Achse und dem Massenpunkt! Wir brauchen also noch den Winkel zwischen
Ortsvektor ~r des Massenpunktes und der z-Achse. Dieser ist nach Def. der Kugelkoor.
3
der Winkel ϑ! Damit gilt: a = r sin ϑ und das auszuwertende Integral heißt nun:
Z
J
2π
Z
π
Z
R
r4 sin3 ϑdrdϑdϕ
= %·
0
0
Z
= %·
2π
Z
0
π
Z
3
R
dϕ
sin ϑ dϑ
r4 dr
0
0
0
| {z } |
{z
} | {z }
2π
1 5
5R
4/3
1
4
= % · 2π · R5 · =
5
3
2
=
mR2
5
4
m
4
3
3 πR
1
4
· 2π · R5 ·
5
3