WAHRSCHEINLICHKEITSTHEORIE 1. Elementare Kombinatorik

WAHRSCHEINLICHKEITSTHEORIE
1. Elementare Kombinatorik
Wir betrachten die Frage wieviele Möglichkeiten es gibt, aus n unterschiedlichen Objekten k auszuwählen. Dabei müssen wir sowohl unterscheiden ob ein Objekt mehrmals ausgewählt werden kann oder nicht,
als auch ob die Reihenfolge der Wahl dieser Objekte berücksichtigt
wird.
Der einfachste Fall ist die Auswahl von k Objekten aus n mit Wiederholung unter Berücksichtigung der Reihenfolge: Wir haben bei der
Wahl vom ersten bis zum k-ten jeweils n Möglichkeiten, also insgesamt
nk .
Bsp.: Es gibt 265 Möglichkeiten Wörter mit 5 Buchstaben aus einem
Alphabet mit 26 Elementen zu bilden.
Die gleiche Fragestellung ohne Wiederholungen gibt für das erste
Element n Möglichkeiten, für das zweite kommen die verbliebenen n−1
Elemente in Frage für das dritte dann n−2 u.s.w. Es gibt also insgesamt
n(n − 1)(n − 2) · · · (n − k + 1) Möglichkeiten.
Bsp.: Es gibt 70 · 69 · 68 Möglichkeiten für die Top-3 Platzierungen
bei einem Wettbewerb mit 70 Teilnehmern.
Ohne Berücksichtigung der Reihenfolge können wir die Zahl der
Möglichkeiten ohne Wiederholung ohne Reihenfolge aus der Zahl der
Möglichkeiten ohne Wiederholung mit Reihenfolge bestimmen indem
wir überlegen wieviele verschiedene Wahlen mit Berücksichtigung der
Reihenfolge einer Wahl ohne Berücksichtigung der Reihenfolge entsprechen:
Es gibt genau k! Möglichkeiten k Elemente anzuordnen, also entsprechen einer Wahl von k unterschiedlichen Elementen aus n k! mit
Berücksichtigung der Reihenfolge und wir sehen, dass es insgesamt
n(n − 1)(n − 2) · · · (n − k + 1)
n
=
k!
k
Möglichkeiten gibt.
Bsp.: Bei einem Kartenspiel mit 32 Karten bekommt jeder Spieler
5 Karten. Für den ersten Spieler gibt es 32
Möglichkeiten bei der
5
27
Verteilung.
Für
den
zweiten dann 5 u.s.w. Für 4 Spieler ergeben
32 27 22 17
sich 5 5 5 5 mögliche Zuteilungen.
1
2
WAHRSCHEINLICHKEITSTHEORIE
Zur Bestimmung der Möglichkeiten mit Wiederholung ohne Reihenfolge auszuwählen überlegen wir dass man jede Wahl von k Elementen
aus n darstellen kann, indem man die Elemente geordnet aufschreibt,
etwa: 1, 2, . . . , n und dann rechts neben jedem Element mit Strichen die
Zahl wie oft dieses Element ausgewählt wurde beschreibt. So entspricht
etwa
1 | | 2 3 | | | | 4 | 5···n | |
der Wahl 2x1, 0x2, 4x3, 1x4 u.s.w. bis 2xn. Und jeder solchen Wahl
von k Strichen zwischen den Zahlen bzw. rechts der Zahl n entspricht
genau eine Wahl von k Elementen. Eine solche Folge hat n+k Eintragungen mit k nichtunterscheidbaren Strichen und den Zahlen 1 bis n
aufsteigend an den verbleibenden Plätzen. Dabei muss an der ersten
Stelle die 1 stehen, da Striche nur rechts von den Zahlen erlaubt sind.
Es gibt also n+k−1
Möglichkeiten die k Striche zu setzen, die freien
k
n Stellen werden dann mit den Zahlen 1 bis n aufsteigend besetzt und
beschreiben so eine Wahl von k aus n Elementen.
Bsp.:
200 Wähler wählen eine von 5 Personen oder ungültig: Es gibt
205
mögliche Wahlausgänge.
6
Zusammenfassend ergibt sich:
Mögl. k aus n ohne Wiederholung mit Wiederholung
zu wählen
mit Reihenn!/(n − k)!
nk
folge.
n
n+k−1
ohne Reihenk
k
folge.
Man kann so Beziehungen zwischen Binomialkoeffizienten durch kombinatorische Überlegungen herleiten: Für die ungeordnete Wahl ohne
Wiederholung sieht man:
Wahlt man aus n Objekten k, so entspricht dem genau eine Wahl
von n − k nicht ausgewählten Objekten. Es gilt also
n
n
=
.
k
n−k
Man kann die Wahl von k aus n Objekten treffen, indem man entweder
das erste Element wählt und aus den verbliebenen n − 1 Elementen
k − 1 auswählt, oder das erste nicht wählt und aus den verbliebenen k
auswählt. Also gilt:
n−1
n−1
n
=
+
.
k
k−1
k
WAHRSCHEINLICHKEITSTHEORIE
3
Oder man wählt zuerst aus den letzten n − k + 1 Elementen das größte
zu wählende m aus, und wählt dann aus den ersten m − 1 die weiteren
k − 1 Elemente. So erhält man
X
n n−1 X
n
m−1
l
=
=
.
k
k−1
k−1
m=k
l=k−1
2. Zufallsgrößen
Wir bezeichnen für eine endliche oder
P abzählbar unendliche Menge
A eine Funktion p : A 7→ [0, P
1] mit a∈A p(a) = 1 eine Wahrscheinlichkeitsdichte. Mit p(B) =
b∈B p(b) wird für alle Teilmengen B
von A eine Wahrscheinlichkeit definiert. A heißt der Wahrscheinlichkeitsraum. Eine reellwertige Funktion X auf P
einem Wahrscheinlichkeitsraum heißt Zufallsgröße. Wir bezeichnen ω∈A: X(ω)=y p(ω) =
p([X −1 (y)) mit P (X = y). Es gilt für die Komplementärwahrscheinlichkeit
p(B { ) d.h. für die Wahrscheinlichkeit der Menge A \ B wegen
P
{
y∈A p(y) = 1 immer p(B ) = 1 − p(B).
Beispiel:
Gilt für alle l Werte k1 , k2 , . . . , kl einer Zufallsgröße X
p(X = ki ) = 1l , so spricht man von einer gleichverteilten Zufallsgröße.
Die Augenzahl eines Würfels ist demzufolge eine gleichverteilte Zufallsgröße. Allgemeiner ist jede k-elementige Folge mit Werten in der
Menge {1, 2, . . . , 6} ein Ereignis aus dem Raum {1, 2, . . .}k mit Wahrscheinlichkeit 1/6k .
Beispiel:
(6 aus 45). Wie groß ist die Wahrscheinlichkeit dass 6
aus 45 angekreuzte Zahlen bei der Lottoziehung gewählt werden? Mit
Berücksichtigung der Reihenfolge sind 45!/39! gleich wahrscheinliche
Ausgänge möglich. Von diesen stimmen 6! mit den angekreuzten über−1
ein. Die Wahrscheinlichkeit zu gewinnen ist also 6!39!/49! = 45
=
6
−7
1, 23 × 10 .
Beispiel: Bernoulliexperiment Ein Versuch mit zwei möglichen Ausgängen wird wiederholt durchgeführt. Dabei trete das Ereignis jeweils mit Wahrscheinlichkeit p ein. Wie groß ist die Wahrscheinlichkeit,
dass das Ereignis bei n Versuchen genau k mal eintritt? Es gibt nk
Möglichkeiten für die Reihenfolge der Versuchsausgänge wenn k Mal
das Ereignis eintritt. Für jede gegebene Folge von k-maligem Eintritt
des Ereignis und n−k-maligem Nichteintreten ist die Wahrscheinlichket
pk (1 − p)n−k . Die Wahrscheinlichkeit dass das Ereignis genau k mal
4
WAHRSCHEINLICHKEITSTHEORIE
eintritt ist also nk pk (1 − p)n−k . Diese Verteilungsfunktion wird Binomialverteilung genannt. Wegen
n X
n k
p (1 − p)n−k = (p + (1 − p))n = 1
k
k=0
erhält man die Gesamtwahrscheinlichkeit 1 über den binomischen Lehrsatz. Wir bezeichnen die entsprechende Zufallsvariable mit
n k
Bn,p : P (Bn,p = k) =
p (1 − p)n−k .
k
Beispiel: In einem Bernoulliexperiment das unendlich oft durchgefürt
wird bezeichne die Zufallsgröße X die Zahl der Versuche vor dem erstmaligen Auftreten des Ereignisses, also P (X = k) = p(1 − p)k . Diese
Verteilung wird als geometrische Verteilung bezeichnet. Es führt die
Berechnung der Gesamtwahrscheinlichkeit auf die geometrische Reihe:
P (X ∈ N0 ) =
∞
X
p(1 − p)k = p
k=0
1
p
= = 1.
1 − (1 − p)
p
Diese Verteilung beschreibt etwa die Wahrscheinlichkeitsverteilung k
Runden in einem Spiel zu überleben, wenn in jeder Runde das Ausscheiden aus dem Spiel mit der Wahrscheinlichkeit p eintritt. Das erstmalige
Eintreten wird auch als Stopzeit bezeichnet, weil man die Beobachtung nach dem erstmaligen Auftreten einstellt, der Zufallsprozess für
Beobachter die nur am erstmaligen Auftreten interessiert sind damit
beendet ist.
Beispiel: Multinomialverteilung Seien in Verallgemeinerung zur Binomialverteilung m Versuchsausgänge möglich dieP
in jeder Runde mit
Wahrscheinlichkeiten pµ , µ = 1, . . . , m auftreten ( m
µ=1 pµ = 1), so ist
die Wahrscheinlichkeit
P für das kµ -malige Eintreten des µ-ten Ereignisses
bei n Versuchen ( m
µ=1 kµ = n)
n!
Qm
µ=1
m
Y
kµ ! µ=1
pkµµ
wie man analog zur Binomialverteilung herleitet.
3. Erwartungswert und Varianz
Für eine Zufallsgröße X bezeichnet
X
E(X) :=
P (X = y)y,
y
WAHRSCHEINLICHKEITSTHEORIE
5
also der über die Wahrscheinlichkeiten gewichtete Mittelwert der möglichen Versuchsausgänge den Erwartungswert. Er beschreibt die durchschnittlich Größe der Zufallswariablen X. Ein Maß für die gewichtete
mittlere Abweichung eines Versuchsausganges von dem Erwartungswert
ist durch die Varianz
Var(X) :=
X
P (X = y)(y − E(X))2
y
gegeben.
Es gilt:
Var(X) =
X
P (X = y)(y − E(X))2
y
=
X
=
X
=
X
P (X = y)(y 2 − 2y E(X) + E(X)2 )
y
P (X = y)y 2 − 2 E(X)
X
P (X = y)y + E(X)2 )
y
y
P (X = y)y 2 − E(X)2 = E(X 2 ) − E(X)2
y
also
Var(X) = E(X 2 ) − E(X)2
(1)
Wir berechnen Erwartungswert und Varianz der geometrischen Verteilung:
Es gilt mit q := 1 − p, da wir im Inneren des Konvergenzkreises die
Differentiation einer Potenzreihe gliedweise ausführen dürfen:
E(X) = p
∞
X
k=0
k
kq = pq
∞
X
kq
k−1
k=1
∞
∞
X
d k
d X k
= pq
q = pq
q
dq
dq
k=1
k=1
p(1 − p)
1−p
d q
1−q+q
1
=
=
= pq
=
−1
= pq
dq 1 − q
(1 − q)2
p2
p
p
also
E(X) =
1
− 1.
p
(2)
6
WAHRSCHEINLICHKEITSTHEORIE
Mit (1) folgt
2
2
Var(X) = E(X ) − (E(X)) = p
= pq 2
∞
X
k=0
∞
X
k 2 q k − (E(X))2
k=0
∞
X
k(k − 1)q k−2 + p
kq k − (E(X))2
k=0
∞
X
d2 k
= pq 2
q + E(X) − (E(X))2
2
dq
k=0
d2 1
+ E(X) − (E(X))2
2
dq 1 − q
2
1
1
2
−3
= pq 2p + − 1 −
−1
p
p
1−p
2(1 − p)2 + p − p2 − 1 + sp − p2
=
=
2
p
p2
= pq 2
Für den Erwartungswert der Binomialverteilung erhält man wegen
n
n!k
n(n − 1)!k
n−1
k=
=
=n
:
k
k!(n − k)!
k(k − 1)!(n − 1 − (k − 1))!
k−1
n n
X
X
n k
n−1 k
n−k
p (1 − p) k =
n
p (1 − p)n−k
k
k
−
1
k=0
k=1
n−1
X n−1
= np
pl (1 − p)n−1−l = np.
l
l=0
Zur Berechnungder Varianz
der Binomialverteilung bemerken wir,
n
n−1 n
dass für k > 0 k = k−1 k gilt und wegen der Faktoren k für die
WAHRSCHEINLICHKEITSTHEORIE
7
P
P
betrachteten Summen nk=0 = nk=1 gilt. Es folgt
n X
n 2 k
2
E(Bn,p ) =
k p (1 − p)n−k
k
k=0
n
X
n−1
=
nkpk (1 − p)n−k
k
−
1
k=1
n−1 X
n − 1 l+1
=n
lp (1 − p)n−1−l + pl+1 (1 − p)n−1−l
l
l=0
n−1 X
n−2 l
= n(n − 1)p
p (1 − p)n−1−l + np(p + 1 − p)n−1
l
−
1
l=1
n−2 X
n−2 m
2
= n(n − 1)p
p (1 − p)n−2−m + np
m
m=0
= n(n − 1)p2 + np
und mit (1)
2
Var(Bn,p ) = E(Bn,p
) − (E(Bn,p ))2 = n2 p2 − np2 + np − n2 p2 = np(1 − p).
4. Konvergenz gegen Poisson oder Exponentalverteilung
Für sehr kleine p und große n ist die Berechnung der Wahrscheinlichkeit P (Bn,p = k) aber sehr aufwendig. Wir betrachten deshalb den
Grenzwert der Wahrscheinlichkeiten P (Bn,pn = k), wobei die Folge (pn )
so gewählt ist, dass für den Erwartungswert E(Bn,p ) = λ gilt. Der Erwartungswert der Binomialverteilung
ist np, also gilt pn = λ/n.
Bn,p
λ n
−λ
Wir erhalten wegen limn→∞ 1 − n = e :
n−k
k λ
n
λ
lim P (Bn,pn = k) = lim
1−
n→∞
n→∞ k
n
n
n −k
k
n(n − 1) . . . (n − k + 1) λ
λ
λ
λk −λ
= lim
1−
1−
= e .
n→∞
nk
k!
n
n
k!
k
Eine Zufallsgröße X auf N0 mit P (X = k) = λk! e−λ heisst Poissonverteilt. Durch sie wird die Wahrscheinlichkeitsverteilung für das
Auftreten von k Ereignissen bei einer großen Zahl von möglichen gleich wahrscheinlichen Einzelereignissen modelliert.
Der Erwartungswert einer Poissonverteilten Zufallsgröße ist
∞
∞
X
X
λk −λ
λk
−λ
k e =e
= λ.
k!
(k
−
1)!
k=0
k=1
8
WAHRSCHEINLICHKEITSTHEORIE
Wegen
E(X 2 ) = e−λ
∞
X
∞
k2
k=0
Xl+1
λk
= λe−λ
λl = λe−λ eλ + λeλ
k!
l!
l=0
= λ(1 + λ)
erhält man für die Varianz V (X) der Poissonverteilung
V (X) = E(X 2 ) − (E(X))2 = λ.
Beispiele sind die Zahl der Anrufe an einem Tag in einem Callcenter,
die Zahl von Sterbefällen in einem Zeitraum bei einer großen Personengruppe u.s.w.
Auch die Zahl von Defekten eines Gerätes in einem Beobachtungszeitraum kann durch eine Poissonverteilung beschrieben werden, wenn
man annimmt, dass das Gerät keinem Alterungsprozess unterliegt und
die Ausfallmöglichkeit durch eine Vielzahl von voneinander unabhängigen Einzelereignissen (Ausfall eines Transistors in einem Schaltkreis)
gegeben ist.
Hat etwa ein solches Gerät im Mittel einen Störfall alle 6 Jahre,
so kann man etwa die Wahrscheinlichkeit für das Auftreten von k
Störfällen in 2 Jahren wie folgt bestimmen: Die Zahl der Ausfälle in
einem Zeitintervall ist Poissonverteilt (wenn amn annimmt, dass keine
Alterungsprozesse eine Rolle spielen). Der Erwartungswert fr die Zahl
von Störfällen in einem Zeitintervall T ist T /6. In unserem Fall ist
das Zeitintervall 2, also ist die Zahl der Störfälle Poissonverteilt mit
Parameter 2/6 = 1/3. Die Wahrscheinlichkeit für das Auftreten von k
Störfällen ist also 3k1k! e−f rac13 .
Durch eine ähnliche Überlegung kann man die Exponentialverteilung
als Grenzverteilung von geometrischen Verteilungen Xg,p mit Parameter p erklären:
Tritt in einem Beobachtungszeitraum der Länge 1 ein Ereignis (z.B.
radioaktiver Zerfall) mit der Wahrscheinlichkeit p ein, so ist die Wahrscheinlichkeit für das erstmalige Eintreten nach n Zeitintervallen (1 −
p)n . Im Zeitintervall T tritt das Ereignis mit Wahrscheinlichkeit (1 −
pn )nT nicht ein, wenn pn die Wahrscheinlichkeit für das Auftreten des
Ereignisses im Zeitintervall n1 ist.
Der Erwartungswert für die Zahl der Zeitintervalle der Länge n1 ist
nach 2 P1n − 1, also ist der Erwartungswert für die Zeit bis zum Eintritt
des Ereignisses n1 p1n − 1 und die Folge der Erwartungswerte dieser
WAHRSCHEINLICHKEITSTHEORIE
9
Zufallsgrößen konvergiert gegen λ1 , wenn die Folge (npn ) gegen λ konvergiert. Für eine solche Folge (pn ) gilt
nT
λ
nT
= e−λT .
lim (1 − pn ) = lim 1 −
n→∞
n→∞
n
Die Wahrscheinlichkeit für das Auftreten des Ereignisses im Zeitintervall [s, t] ist also e−λs −e−λt . Demzufolge erfüllt
WahrscheinlichkeitsR tdie−λr
−λr
dr = e−λs − e−λt .
dichtefunktion ρ(r) = λe
die Bedingung s λe
Sie ist das kontinuierliche Analogon einer diskreten WahrscheinlichkeitsdichteR auf einer abzählaren Menge. Man
R ∞ erhält für den Erwart∞
ungswert 0 λte−λt dt = λ1 und die Varianz 0 t − λ1 2λe−λt dt = λ1 .
Eine Zufallsgröße auf R+ mit der Wahrscheinlichkeitsdichtefunktion
ρ(r) = λe−λr heisst exponentialverteilt
5. Zentraler Grenzwertsatz und Gesetz der großen
Zahlen
Wir haben den Erwartungswert als den über die Wahrscheinlichkeiten gewichteten Mittelwert der Zufallsgröße definiert. Ist der Ausgang eines Experimentes durch eine Zufallsgröße X beschrieben, die
einen endlichen Erwartungswert E(X) hat, so gilt für die Folge (X̄n ),
die man durch den Mittelwert von n Ausgängen des Experimentes und
beliebiges > 0 das schwache Gesetz der großen Zahlen:
lim P (|Xn − E(X)| > ) = 0.
n→∞
Ist etwa bei einem fairen Spiel (Erwartungswert 0) P (X = 1) =
P (X = −1) = 1/2 (Münzwurf), so sagt das schwache Gesetz der großen
Zahlen, dass mit fortschreitender Spieldauer n die Wahrscheinlichkeit
einen Gewinn oder Verlust zu machen der größer als n ist gegen 0
konvergiert, der mittlere Gewinn wird sich also mit zunehmender Spieldauer mit immer größerer Wahrscheinlichkeit um weniger als vom
Erwartungswert 0 unterscheiden.
Satz 5.1. (Markov’sche Ungleichung) Für eine positive Zufallsgröße
X und a > 0 gilt:
E(X)
.
P (X ≥ a) ≤
a
Beweis. Sei ρ die Wahrscheinlichkeitsdichte der Zufasllgröße X, so gilt
Z ∞
Z ∞
Z ∞
E(X) =
xρ(x) dx ≥
xρ(x) dx ≥ a
ρ(x) dx = aP (X ≥ a).
0
a
a
10
WAHRSCHEINLICHKEITSTHEORIE
Satz 5.2. (Tschebyschew’sche Ungleichung) Für eine Zufallsgröße mit
endlicher Varianz σ 2 und a > 0 gilt:
σ2
P (|X − E(X)| ≥ a) ≤ 2 .
a
Beweis. Es folgt aus der Markov’schen Ungleichung für die Zufallsgröße (X − E(X))2 , die positiv ist und Erwartungswert σ 2 hat:
P (|X − E(X)| ≥ a) = P ((X − E(X))2 ≥ a2 ≤
σ2
.
a2
Aus dem schwachen Gesetz der großen Zahlen folgt nicht unmittelbar, dass mit zunehmender Spieldauer der mittlere Gewinn gegen 0
konvergiert, da man auch für beliebig große n immer wieder große mittlere Abweichungen haben könnte. Man kann aber auf dem Raum der
Folgen von Experimenten eine Wahrscheinlichkeit definieren. Dann gilt
sogar das starke Gesetz der großen Zahlen: P (limn→∞ X̄n = µ) = 1.
Ist darüberhinaus auch die Varianz σ 2√von X endlich, so kann man
zeigen, dass die Folge von Zufallsgrößen ( nX̄n ) gegen eine kontinuierliche Verteilung konvergiert, die nur von der Varianz σ 2 und dem Erwartungswert µ der Zufallsgröße X abhängt und durch die Dichtefunktion
2 !
1
1 t−µ
ρ(t) = √ exp −
2
σ
σ 2π
gegeben ist. Dies ist die Aussage des zentralen Grenzwertsatzes. Die so
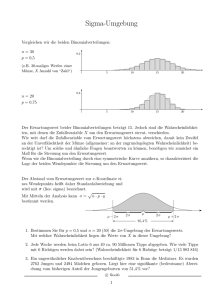
erhaltene Wahrscheinlichkeitsverteilung auf R wird Normalverteilung
Nσ,µ genannt.
Mit ihr modelliert man Versuche, deren Ausgang von einer Vielzahl
unabhängiger Faktoren abhängt, wenn die einzelnen Faktoren den Ausgang wenig beeinflussen. Sind etwa eine große Zahl N von Verbrauchern unabhängig voneinander mit einer gewissen Wahrscheinlichkeit p
ein oder ausgeschaltet, so beschreibt die Binomoalverteilung die Wahrscheinlichkeitsverteilung für die Zahl der eingeschaltenen Verbrauchern. Für große N konvergieren die Wahrscheinlichkeiten aber gegen
0, weshalb man eine bessere Vorstellung von der Verteilung gewinnt,
wenn man die (diskrete) Verteilung der Zahl der Verbraucher durch die
(kontinuierliche) Normalverteilung approximiert.