3.3 Heterogene Oligopole und monopolistische Konkurrenz

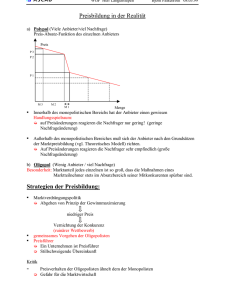
3.3 Heterogene Oligopole und monopolistische Konkurrenz
In diesem Abschnitt werden wir sehen, daß das Bertrand-Ergebnis in homogenen Märkten stark
abgeschwächt werden kann, wenn der Markt nicht mehr homogen ist. Zunächst gehen wir von
nur 2 Unternehmen aus. Zur Vereinfachung gehen wir auch von linearen Nachfragefunktionen aus.
Damit wir einfacher mit der Situation bei Mengenentscheidungen vergleichen können, gehen wir
von folgenden Preis-Absatzfunktionen aus:
P1 (x 1, x 2) = a - bx 1 - θbx 2
P2 (x 1, x 2) = a - bx 2 - θbx 1
Daraus ergeben sich die Nachfragefunktionen
x1 ( p1 , p 2 ) =
a
1
θ
−
p1 +
p2
2
b(1 + θ) b (1 − θ )
b (1 − θ 2 )
x 2 ( p1 , p2 ) =
a
1
θ
−
p2 +
p1
2
b(1 + θ) b(1 − θ )
b(1 − θ 2 )
Falls diese Ausdrücke negative Ergebnisse haben, wird die Nachfrage gleich 0 gesetzt.
Auch die Kostenfunktionen seien linear und für beide Unternehmen gleich: Ci(x i) = cx i. Für die
Paramter gelte a(1-θ) > c und 1 > θ > 0. Die Gewinnfunktion des ersten Unternehmens ist daher
für positive Nachfrage:
Π 1(p1, p2) = (p1 - c) x 1 (p1, p2)
Die Gewinnfunktion des zweiten Unternehmens ist analog für positive Nachfrage
Π 2(p1, p2) = (p2 - c) x 2 (p1, p2)
Fassen wir diese beiden Gewinnfunktionen als Nutzenfunktionen zweier Spieler auf, können wir
uns nach dem Nash-Gleichgewicht des entsprechenden Spiels fragen.
Betrachten wir zunächst die "Reaktionsfunktion" des ersten Unternehmens. Dazu müssen wir
beachten, daß durch einen zu hohen Preis die eigene Nachfrage auf 0 absinkt und durch einen
sehr niedrigen Preis dasselbe für die Nachfrage des Konkurrenten gelten kann. Die eigene
Nachfrage ist genau dann positiv, wenn
(1 - θ)a - p1 + θp2 > 0 ⇔ p2 > p1/θ - (1 - θ)a/θ
2
Die Nachfrage des Konkurrenten ist genau dann positiv, wenn
a - bp2 + θbp1 > 0 ⇔ θp1 + (1 - θ)a > p2
Gehen wir nun zunächst davon aus, daß diese Konstellationen zutreffen. Dann ergibt sich in
diesem Bereich die "Reaktionsfunktion" des ersten Unternehmens aus der Maximierung von
Π 1(p1, p2) bzgl. p1:
(1 - θ)a + c - 2p1 + θp2 = 0 ⇔ p2 = -((1 - θ)a + c)/θ + 2p1/θ
⇔ p1(p2) = ((1 - θ)a + c)/2 + θp2/2
Daran kann man ablesen, daß die Positivitätsbedingungen für die Nachfrage für das
Gleichgewicht nie bindend werden. Dies sieht man am einfachsten, wenn man sich die Situation
graphisch veranschaulicht:
p2
x2 < 0
x2 > 0
p 2 (.)
p 1 (.)
((1-θ)a+c)/2
(1-θ)a
x1 < 0
p1
In der Graphik sind die beiden Begrenzungslinien für die Bedingung x i > 0 eingetragen. Die
Begrenzungslinie für x 1 > 0 hat eine geringere Steigung als die "Reaktionsfunktion" des ersten
Unternehmens. Daher wählt - naheliegenderweise - das erste Unternehmen nie einen Preis, der
seine Nachfrage auf Null drücken könnte.
Daraus liest man nun ab, daß sich die relevanten "Reaktionsfunktionen" genau einmal schneiden.
Wir haben also sowohl Existenz als auch Eindeutigkeit des Nash-Gleichgewichts. Berechnet man
aus den obigen Gleichungen das Gleichgewicht, so ergibt sich:
p1 = p2=
(1 − θ )a + c
(1 − θ )( a − c)
= c+
2−θ
2−θ
Im Gegensatz zu dem "reinen" Bertrand-Modell ergibt sich damit nun ein Preis deutlich über den
Grenzkosten, solange θ < 1.
3
Der Parameter θ gibt die Substituierbarkeit wieder. Wenn dieser Parameter gleich 0 ist, ist die
Nachfrage der einzelnen Unternehmen bzgl. der Preise völlig unabhängig voneinander. Die
Kunden der beiden Unternehmen betrachten dann die beiden Güter als nicht substituierbar. Sie
stellen schlichtweg zwei völlig unterschiedliche Güter dar. Je höher der Parameter ist, desto höher
ist auch die Beweglichkeit der Nachfrager. Wenn ein Unternehmen seinen Preis erhöht, werden
θ) Kunden zu dem anderen Unternehmen "überlaufen". Sie betrachten
also die beiden Güter als zunehmend substitutiv. Wenn θ = 1 gilt, sind beide Güter perfekte
Substitute (vgl. die obigen Preis-Absatzfunktionen!). Dann sinken die Preise auf die Grenzkosten.
In diesem Fall ist die oben getroffene Annahme a(1-θ) > c nicht mehr möglich. Diese wurde
jedoch nur getroffen, um nicht mehrere Fallunterscheidungen vornehmen zu müssen. Nimmt man
in Kauf, daß man die Zeichnung für a(1-θ) < c entsprechend anpassen muß, so braucht man nur
die Annahme a > c. Die entsprechende Zeichnung findet man z.B. in Martin.
Würde man die obige Analyse mit Mengenentscheidungen durchführen (heterogenes CournotModell), so würden sich niedrigere Preise und Gewinne einstellen. Die entsprechenden
Rechnungen bleiben dem Leser als Übung überlassen.
Stattdessen wollen wir hier untersuchen, wie die Preiskonkurrenz zwischen den beiden
oligopolistischen Unternehmen im Verhältnis zu einem 2-Produktmonopolisten auf den Preis
wirkt. Berechnet man die gewinnmaximalen Preise eines solchen Monopolisten, so ergibt sich:
p1 = p2 =
a+c
2
Daraus läßt sich schnell ablesen, daß dieser Preis höher ausfällt. Dies ist nicht überraschend. Bei
positivem θ übt jedes Unternehmen über seinen Preis einen positiven externen Effekt auf den
Kokurrenten aus. Da unabhängige Unternehmen diesen Effekt nicht beachten, wählen sie im
Verhältnis zu einem 2-Produktmonopolisten, der diesen Effekt internalisieren kann, einen zu
geringen Preis. Das Ergebnis ist demnach nicht überraschend. Man beachte jedoch, daß sich
dieses Ergebnis herumdreht, wenn die Güter Komplemente sind. Aus denselben Gründen wird
ein 2-Produktmonopolist in dem Fall von Komplementen einen niedrigeren Preis fordern als dies
unabhängige Unternehmen tun. Mehr Wettbewerb ist also nicht unbedingt besser für die
Konsumenten.
Die obige Analyse läßt sich ohne große Probleme auf mehr als zwei Unternehmen übertragen. Bei
n Unternehmen, wird die Nachfrage wie folgt aussehen (abgeleitet aus der Verallgemeinerung
obiger Preis-Absatzfunktionen):
4
x i ( pi , p) =
1
1 
nθ

a −  pi +
( pi − p)  ,


1 + (n − 1) θ b  
1− θ
1
p . Man beachte, daß die Nachfrage sich nun auf mehr Unternehmen aufteilt
n∑j j
und daß deshalb die Nachfrage pro Unternehmen sinkt. Daraus ergibt sich der
Gleichgewichtspreis
wobei p =
pi = c +
(1 − θ)( a − c)
.
2 + ( n − 3)θ
und die sich damit einstellenden Gewinne
2
1 (1 + ( n − 2)θ )(1 − θ)  a − c 
Π i ( n) =

 .
b
1 + ( n − 1)θ
 2 + ( n − 3)θ 
Daraus läßt sich nun unschwer ablesen, daß sowohl die Preise als auch die Gewinne mit
steigenden Unternehmenszahlen sinken. Mehr Wettbewerb führt hier zu einer besseren
Versorgungslage. Wenn n gegen unendlich strebt, konvergieren Preise und Gewinne gegen Null.
Das drückt man typischerweise so aus: Freier Eintritt von Unternehmen führt zu einer effizienten
Versorgung (und Preissetzung).
Allerdings ist die kritischste Annahme, die wir hier getroffen haben, die der Linearität der Kosten.
In aller Regel ist Produktion mit Fixkosten verbunden. Im einfachsten Fall haben wir dann eine
Kostenfunktion C(x) = F + cx. Unter diesen Umständen wäre der Gewinn jedes Unternehmens
Π i(n) - F. Folglich werden nicht mehr unendlich viele Unternehmen eintreten. Vielmehr werden
nur solange Unternehmen eintreten, wie der zu erwartende Gewinn nicht negativ ist. Formal
werden nur soviele Unternehmen n* eintreten, wie durch die Ungleichungen
Π i(n*) - F ≥ 0, Π i(n* + 1) - F < 0
charakterisiert sind. Diese Situation läßt sich auch als eine Art "Tangentenlösung" graphisch
charakterisieren. Diese Tangentenlösung spielt in der Theorie der monopolistischen Konkurrenz
eine wichtige Rolle. Deshalb werden wir sie hier im Kontext der Oligopoltheorie schon einmal
besprechen.
Dazu gehen wir davon aus, daß n* durch Π i(n*) - F = 0 charakterisiert ist. Nur in diesem Fall
haben wir eine "richtige" Tangentenlösung. Die Tangentialität bezieht sich auf die relevante
Nachfragekurve eines Unternehmens und die Durchschnittskostenkurve. Die Bedingung für n*
5
bewirkt, daß die beiden Kurven tangential zueinander sein müssen. Betrachten wir dazu die
relevante Nachfragefunktion. Bei der eigenen Wahl des Preises geht ein Unternehmen davon aus,
daß die anderen Unternehmen ihre Gleichgewichtspreise, p *, wählen. Setzt man die obigen
Preise ein, so ergibt sich für die Nachfragefunktion
x i ( p, p*) =
1
1  ( 2a (1 − θ ) + c( n − 1)θ )(1 + (n − 2) θ 1 + ( n − 2) θ 
−
p .
1 − (n − 1)θ b 
(1 − θ)( 2 + (n − 3) θ)
1− θ

Daraus kann man nach einigen Rechnungen finden, daß die Steigung der Nachfragefunktion mit
steigendem n zunimmt und daß der Preis, bei dem die Nachfragefunktion Null wird, mit
steigendem n fällt. Betrachten wir diese Situation in der folgenden Graphik.
p
Durchschnittskostenkurve
I
II
p*
III
x*
xi
Die mit römischen Zahlen gekennzeichneten Kurven repräsentieren die obigen relevanten
Nachfragefunktionen für verschiedene n. Die mit I gekennzeichnete Kurve läßt offenbar positive
Gewinne zu: Z.B. der für x* erreichbare Preis liegt über den Durchschnittskosten. Also ergibt
sich ein positiver Gewinn und es findet weiterer Eintritt statt. Bei der mit III gekennzeichneten
Nachfragefunktion sind nur Verluste zu erwirtschaften. Die Nachfragekurve liegt vollkommen
unter der Durchschnittskostenkurve. Sie repräsentiert eine Anzahl von Unternehmen, die alle
Verluste machen. Folglich muß der Eintrittsprozeß vorher zum Erliegen gekommen sein. Die mit II
gekennzeichnete Nachfragefunktion schließlich erlaubt, bei (x*, p*) gerade die Kosten zu
decken. Ein positiver Gewinn ist nicht möglich. Dies muß daher gerade die Situation sein, in der
so viele Unternehmen eingetreten sind, daß niemand positive Gewinne machen kann, jedoch auch
niemand Verluste macht. Sie charakterisiert folglich die Anzahl n*.
Die "Tangentenlösung" besteht offenbar darin, die von der Anzahl der Unternehmen abhängende
relevante Nachfragekurve zu finden, die mit der Durchschnittskostenkurve tangential wird. Die
Anzahl, die diese Nachfragekurve charakterisiert, ist die Anzahl der eintretenden Unternehmen.
Offensichtlich kann diese Tangentialität nur erreicht werden, wenn es "zufällig" ein n gibt, bei der
die entsprechende Nachfrage tangential wird. Es könnte zum Beispiel sein, daß die mit I
6
gekennzeichnete Nachfragekurve zu einer Anzahl n gehört und die mit III gekennzeichnete zu der
Anzahl n+1. Zu der mit II gekennzeichneten Kurve gäbe es also gar keine entsprechende Anzahl.
n gerade die Anzahl der eintretenden Unternehmen, obwohl die
Nachfragekurve und die Durchschnittskostenkurve nicht tangential sind. Daher ist diese
graphische "Lösung" nur dann zu empfehlen, wenn von vorneherein klar ist, daß n* sehr groß sein
wird. Bei sehr großen n werden sich die Nachfragekurven nicht mehr sehr unterscheiden, wenn
man ein zusätzliches Unternehmen hinzufügt. Jedoch wird auch in diesem Fall die Lösung nur eine
gewisse Approximation an das exakte Ergebnis sein können.
Bei der monopolistischen Konkurrenz stellt man sich typischerweise einen Markt mit sehr vielen
Unternehmen vor, deren Produkte Substitute zueinander sind, jedoch nicht perfekte Substitute. In
der Tat kam die ursprüngliche Motivation zur Formulierung dieser Theorie von dem Unbehagen,
das sich bei der Betrachtung der vollständigen Konkurrenz als einzigem Marktmodell einstellen
muß. Es wurde insbesondere hervorgehoben, daß jedes Unternehmen ein etwas anderes Gut
anbietet. Man wollte einem Modell von intensivem Wettbewerb ein monopolistisches Element, die
durch die (begrenzte) Einmaligkeit eines Gutes hervorgerufen wird, hinzufügen. Daher erklärt sich
zum einen die Konzentration auf eine "Tangentenlösung" als graphisches Hilfsmittel zur
Beschreibung des Marktergebnisses. Wie wir gesehen haben, braucht man dazu keine
Modellbildung, die über das Oligopolmodell hinausgeht. Jedoch zeichnet sich die Modellbildung
der monopolistischen Konkurrenz auch noch durch einen anderen Aspekt aus. Sie ignoriert im
Prinzip die strategische Interdependenz zwischen den Unternehmen. Damit fällt sie auf ein logisch
deutlich unbefriedigenderes Niveau zurück. Hätte die Modellbildung der monopolistischen
Konkurrenz nicht insbesondere in der neuen Außenhandelstheorie eine enorme Resonanz
gefunden, lohnte sich der Aufwand kaum, diese Modelle zu besprechen. Angesichts dieses
Interesses werden wir im folgenden kurz das Vorgehen und dessen Begründung im Rahmen der
Theorie der monopolistischen Konkurrenz skizzieren.
In den Anwendungen (beispielsweise) der Außenhandelstheorie werden die Nachfragesysteme
meist aus der Nutzenfunktion eines repräsentativen Konsumenten abgeleitet, um die
Wohlfahrtsanalyse zu erleichtern. Als Standardbeispiel wird dazu fast durchgängig von der
Nutzenfunktion (0<α,ρ<1)
u( x 0 , x1 ,..., x n ) =
x01− α
α
ρ ρ
x
i =1 i
[∑ ]
n
7
ausgegangen, weil sie bei den in den Anwendungen interessanten Fragestellungen zu recht
übersichtlichen Formeln führt, die zudem gut interpretierbar sind. Gehen wir nun davon aus, daß
ein Konsument mit dieser Nutzenfunktion folgender Budgetgleichung unterliegt:
p0 x0 + ∑i =1 pi xi = m
n
Daraus läßt sich über die Maximierung des Nutzens folgende Nachfragefunktion ableiten:
x0 =
(1 − α ) m
p0
1
−
1− ρ
pi
x i = αm
∑
ρ
−
1−ρ
p
j =1 j
n
Die Güter i = 1,...,n werden als Varianten eines Gutes angesehen, von denen jede Variante von
genau einem Unternehmen angeboten wird. Wir sehen, daß die Nachfrage nach der Variante i
von allen Preisen abhängt. Der "Trick" in der Modellbildung der monopolistischen Konkurrenz
besteht darin, die Einflüsse des Terms, der oben im Nenner steht, zu ignorieren. Um der
Begründung nachzugehen, ist es hilfreich, sich die Herleitung des obigen Terms für die Nachfrage
nach i anzusehen. Die Bedingung erster Ordnung für die Bestimmung von x i ist
αx01−α
α
−1
ρ ρ
x
xiρ−1
j =1 j
[∑ ]
n
= λpi ,
wobei λ der Lagrangemultiplikator der Budgetrestriktion ist und den Grenznutzen des
Einkommens angíbt. Dieser läßt sich zusammen mit den anderen Bedingungen erster Ordnung
berechnen:
x 1−α
λ= 0
m
α
ρ ρ
x
j =1 j
[∑ ]
n
Benutzt man dies in der vorangegangenen Gleichung, so ergibt sich
αmxiρ−1 = pi
oder
[∑ x ]
n
j =1
ρ
j
8
x i = ( αm)
1
1−ρ
−
pi
1
1−ρ
[∑ ]
xρ
j =1 j
n
1
−
1−ρ
.
Es ist nun instruktiv, den Einfluß des Preises pi auf die Nachfrage x i zu untersuchen. Eine
Preisänderung hat erstens einen direkten Effekt auf x i. Dieser Effekt wird durch den
entsprechenden Preisterm in der letzten Gleichung wiedergegeben. Eine Preisänderung hat jedoch
auch einen indirekten Effekt auf die Bewertungsgrundlage, den Grenznutzen. Dort gehen die
Mengen aller Güter ein. Eine Preisänderung kann daher alle Mengen ändern, somit die
Bewertungsgrundlage und damit die Nachfrage selbst. In der Theorie der monopolistischen
Konkurrenz wird genau dieser indirekte Effekt vernachlässigt. Die Idee dabei ist, daß die
Preisänderung eines einzelnen von sehr vielen (!) Unternehmen nur einen sehr geringen Einfluß auf
die gesamte Nachfrage nach allen Varianten zusammen hat (genauer auf den Ausdruck in eckigen
Klammern). Inwieweit dies berechtigt ist, kann man sich am einfachsten klarmachen, wenn man
die beiden Ausdrücke für die Nachfrage nach der Variante i miteinander vergleicht. Der Einfluß
auf den Ausdruck in eckigen Klammern in der letzten Gleichung entspricht dem Ausdruck im
Nenner in der Gleichung weiter oben. Betrachten wir nun den Einfluß einer Preisänderung auf
diesen Term. Dazu zerlegen wir die Nachfrageänderung in den direkten Effekt und den indirekten
Effekt:


1
 − 1−ρ
∂xi
 ∂p
= αm i
∂pi
 ∂pi


 n −ρ 
∂ ∑ j=1 p j 1−ρ 
ρ −1
 n



−

 ∑ p j 1−ρ  + 
j =1
∂pi




−1


1 
−

pi 1−ρ 



Der erste Term in der geschweiften Klammer entspricht dem direkten Effekt. Von Interesse ist
also der zweite Term. Führt man die Differentiation aus, so erhält man für den zweiten Term
−
2
1−ρ
pi
ρ
2
ρ
1− ρ 

−
n
 ∑ p 1− ρ 
 j =1 j 


Da die Nachfragefunktionen für alle Varianten dieselbe Struktur haben, ist im Gleichgewicht
davon auszugehen, daß alle Unternehmen denselben Preis fordern werden. Setzen wir alle Preise
gleich, so ergibt sich für diesen Ausdruck
9
−
2
1−ρ
pi
ρ
ρ
1
=
.
2ρ
2 2
1− ρ
1 − ρ n pi
−
n 2 pi 1−ρ
Damit wird klar, daß dieser Ausdruck schnell gegen Null konvergiert, wenn n gegen unendlich
strebt. Für "sehr viele" Unternehmen ist es daher approximativ korrekt, den indirekten Effekt zu
vernachlässigen. Man beachte dabei, daß der erste direkte Effekt ebenfalls gegen Null
konvergiert. Würde man auch bei ihm gleiche Preise annehmen, so würde in dem Ausdruck ein
Term 1/n vorkommen. Dieser konvergiert jedoch langsamer gegen Null als 1/n2. Die
Approximation ist daher in gewissen Grenzen zu vertreten.
Man mag sich nun fragen, warum diese Approximationen vorgenommen werden. Ein zentraler
Grund für diese Approximation und die Wahl dieser spezifischen Nutzenfunktion ist die Tatsache,
daß dann die Preiselastizität der Nachfrage eine Konstante ist. Kehren wir zu dem ersten
Ausdruck für die Nachfrage nach der Variante i zurück:
1
−
1− ρ
pi
x i = αm
∑
ρ
−
1−ρ
p
j =1 j
n
und betrachten den Ausdruck im Nenner als Konstante bzgl. des eigenen Preises. Dann ergibt
sich die Preiselastizität der Nachfrage als
−
1
.
1−ρ
Daraus folgt bei konstanten Grenzkosten (wie sie fast ausschließlich in den Anwendungen
angenommen werden), daß der gewinnmaximierende Preis die Bedingung
p−c
= 1−ρ
p
erfüllt. Daraus läßt sich sofort der Preis und der Gewinn eines jeden Unternehmens angeben: Der
Preis ist
p=
c
.
ρ
10
Man beachte, daß dieser Preis nicht von der Anzahl der Unternehmen abhängt. Dies impliziert die
"relevante" Nachfragefunktion (s.o. "Tangentenlösung")
ρ
1
−
 c ρ
αm
xi =
 
n  ρ
−
pi
1
1−ρ
,
die gewinnmaximale Menge
αmρ
nc
und den Gewinn pro Unternehmen
αm(1 − ρ)
.
n
Offenbar sind dies sehr einfach zu handhabende Ausdrücke, die die darauf aufbauende Analyse
deutlich vereinfachen. Wir sehen hier auch, daß der Gewinn nicht mehr von den Grenzkosten
abhängt. Außerdem läßt sich nun leicht die Anzahl von Unternehmen angeben, die eintreten, wenn
sie mit den Fixkosten F konfrontiert sind:
αm(1 − ρ)
F
Auch hier wird wieder implizit von einer sehr großen Anzahl von Unternehmen ausgegangen,
sonst macht die "Tangentenlösung" keinen Sinn.
Als Fazit können wir festhalten, daß die Modellbildung der monopolistischen Konkurrenz auf
Kosten einiger Approximationen deutlich einfachere Endergebnisse aufweist als die
oligopolistische Modellierung. Leider ist es im Einzelfall nicht so einfach zu überprüfen, welchen
Fehler man mit diesen Approximationen macht.
Literatur:
Güth, W. (1994): Markt- und Preistheorie, Springer Verlag, Kap. 1.4 (Achtung: Güth nennt die
obigen Preisgleichgewichte Cournotgleichgewicht)
Martin, S. (1993): Advanced Industrial Economics, Blackwell, Kap. 2 und Kap. 14
Tirole, J. (1989): The Theory of Industrial Organization, MIT-Press, Kap. 7.2, 7.5.2