Elektrisches Feld

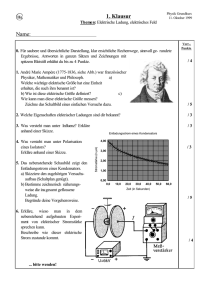
Physik für Mediziner,
Zahnmediziner und
Pharmazeuten

SS2000
18.-20.Vorlesung
2.6./5.6./6.6.2000
Prof. Dr. Alois Putzer
1
Zurück zur ersten Seite
Plan : Nächste Vorlesungen

Heute:
Elektrizität

Danach :
Optik
Röntgenstrahlung
Radioaktivität
Nuklearmedizin
Elektromagnetische
Wellen
Tomographie, Laser,......
2
Zurück zur ersten Seite
Elektrostatik






Elektrische Kräfte bestimmen den Aufbau
der Materie.
Positive und negative Ladung
Proton (+), Elektron (-)
Elektrisch neutraler Zustand : Gleiche
Zahl von positiven und negativen
Bausteinen.
Freie Ladung erhält man durch Trennung
von negativen und positiven
Ladungsträgern.
Elektrostatik : Untersuchung von freien
3
ruhenden Ladungen.
Zurück zur ersten Seite
Elektrische Kraft



Elektrische Kräfte gehen von Ladungen
aus und wirken auf Ladungen.
Ladung : 1 C= 1As = 6,242 1018qe (Elektron)
qe = 1,602 10-19 C
Coulomb Gesetz (1785)

Fel 
ε
1 Q1Q 2 
er
4π ε 0 r²

8,8510
o
4
12
As
Vm
Zurück zur ersten Seite
Einheiten der Elektrizität





Strom
: I : Ampere : A (Grundgröße)
Ladung : Q: Coulomb : C = As
Spannung : U :Volt
: V = Nm/As
Leistung : P :Watt
: W = VA
Energie : W :
: Ws = VC = J
5
Zurück zur ersten Seite
Elektrisches Feld(1)



Jede elektrische Ladung ist immer von
einem elektrischen Feld umgeben.
Bringt man eine Probeladung q in ein
elektrisches Feld, so wirkt die
Coulombkraft auf diese.
Damit erhalten wir für das elektrische
Feld
6

 Fel
E
q
Zurück zur ersten Seite
Elektrisches Feld (2)



Das elektrische Feld einer
Punktladung:

 F
1 Q
E 
er
q 4π  0 r²
[E] = N/As = V/m
Die Richtung des Feldvektors zeigt in
die Richtung in die sich eine positive
Probeladung bewegen würde.
7
Zurück zur ersten Seite
Feld einer Punktladung
8
Zurück zur ersten Seite
Feld zweier ungleicher Ladungen
9
Zurück zur ersten Seite
Feld zweier gleicher Ladungen
10
Zurück zur ersten Seite
Elektrisches Feld (3)





Richtung der Feldlinien = Richtung des elektrischen Feldes
Dichte der Feldlinien ist proportional zur Stärke
des elektrischen Feldes.
Elektrische Feldlinien beginnen und enden
immer auf Ladungen.
Das elektrische Feld steht senkrecht auf einer
Leiteroberfläche=> der Innenraum eines
geschlossenen Leiters ist feldfrei (und damit
ladungsfrei.)
Das elektrische Feld läßt sich abschirmen:
11
Faradaykäfig.
Zurück zur ersten Seite
Elektrische Spannung(1)




Verschiebung einer Ladung im elektrischen
Feld erfordert, analog zur Bewegung einer
Masse im Gravitationsfeld, die Arbeit
W=F s = q E s = q E (r1 - r2) = q U12
Die Größe U nennt man die
Potentialdifferenz oder elektrische
Spannung zwischen den Punkten 1 und 2.
Die Spannung beträgt 1V, wenn zur Verschiebung der Ladung 1C die Arbeit 1J
erforderlich ist.
12
Zurück zur ersten Seite
Elektrische Spannung(2)



Für die Spannung zwischen zwei Metallplatten im Abstand d erhält man
U = Ed (E = U/d)
Für die Kraft auf die Probeladung q ergibt
sich:
F=qE = qU/d
und für die Beschleunigung im elektrischen Feld:
a=F/m = q/m U/d
13
Zurück zur ersten Seite
Ladungstrennung durch Influenz

Bringt man einen ungeladenen
metallischen Leiter in ein elektrisches
Feld, so werden die leicht
beweglichen Ladungsträger
(Elektronen) so verschoben, daß im
Inneren kein resultierendes
elektrisches Feld vorhanden ist.
14
Zurück zur ersten Seite
Influenz
15
Zurück zur ersten Seite
Dielektrikum
16
Zurück zur ersten Seite
17
Zurück zur ersten Seite
Speicherung von Ladungen:Kondensatoren

Die Ladungsmenge Q hängt ab von
der Spannung U, der Fläche der Platten A
dem Abstand zwischen den Platten d
Q = C U bzw. C=Q/U
(C : Kapazität : Farad [F]
A
C ε o
d
18
Zurück zur ersten Seite
Elektrisches Feld mit Dielektrikum

Bei Nichtleitern wird das Feld im Inneren
nur geschwächt, da die Ladungen sich
nicht bewegen sondern nur ausrichten
können.
19
Zurück zur ersten Seite
Kondensator mit Dielektrikum

Bringt man ein Dielektrikum zwischen die
Kondensatorplatten, so ändert sich die
Kapazität des Kondensators.
20
Zurück zur ersten Seite
Elektrische Leitung in Metallen
21
Zurück zur ersten Seite
Drehspulinstrument
22
Zurück zur ersten Seite
Schiebewiderstand
23
Zurück zur ersten Seite
Ohmsches Gesetz : U = R I
24
Zurück zur ersten Seite
Elektrolyse
25
Zurück zur ersten Seite
Galvanische Elemente
26
Zurück zur ersten Seite
Faraday-Gesetz




Fließt ein StromI so wird in der Zeit t
die Ladungsmenge Q = I t von den
Ionen transportiert. Trägt ein Ion die
Ladung z e so sind es N = Q/ze
Ionen.
m(g)=Molmasse/z •Q/F
F = e NA = 96485 C/mol
n(mol) = Q/z.F
27
Zurück zur ersten Seite
Elektrizitätsleitung im Vakuum
28
Zurück zur ersten Seite
Zählrohr
29
Zurück zur ersten Seite