Lernziele Konvergenz von Zahlenfolge Def - ttp

Folgen (Prof. Dr. Wagner – FB AI)
Lernziele Konvergenz von Zahlenfolge
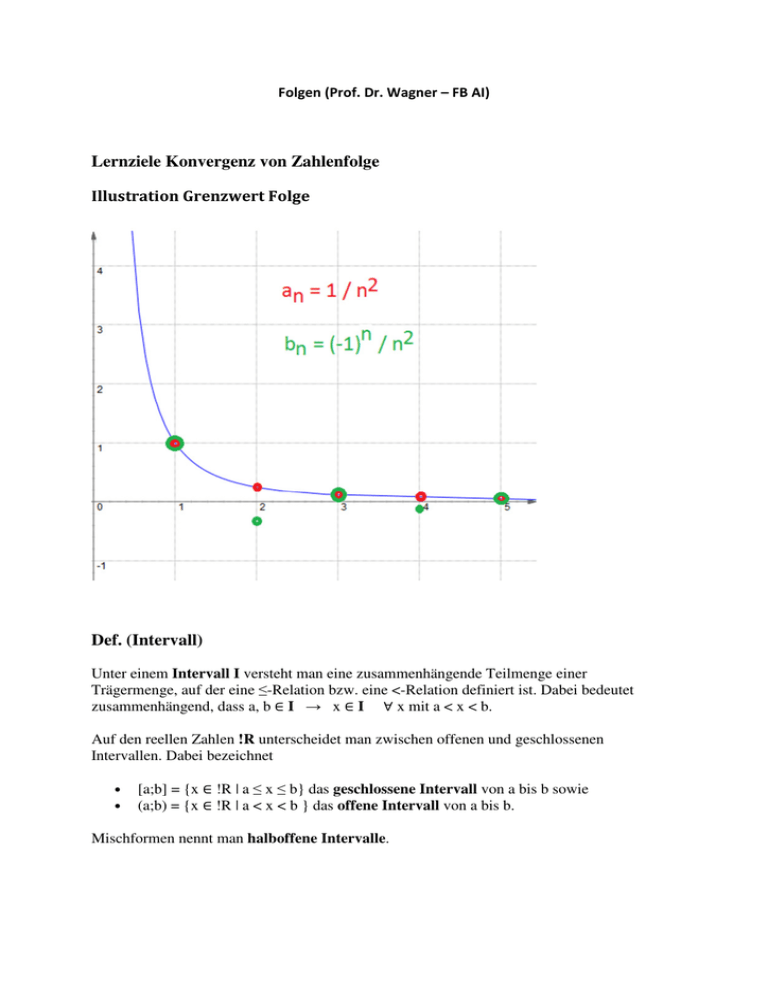
Illustration Grenzwert Folge
Def. (Intervall)
Unter einem Intervall I versteht man eine zusammenhängende Teilmenge einer
Trägermenge, auf der eine ≤-Relation bzw. eine <-Relation definiert ist. Dabei bedeutet
zusammenhängend, dass a, b ∈ I → x ∈ I ∀ x mit a < x < b.
Auf den reellen Zahlen !R unterscheidet man zwischen offenen und geschlossenen
Intervallen. Dabei bezeichnet
•
•
[a;b] = {x ∈ !R | a ≤ x ≤ b} das geschlossene Intervall von a bis b sowie
(a;b) = {x ∈ !R | a < x < b } das offene Intervall von a bis b.
Mischformen nennt man halboffene Intervalle.
Def. (ε - Umgebung)
Die ε-Umgebung U (a;ε) der reellen Zahl a ist die Menge aller Zahlen x aus !R, für die der Betrag der
Differenz a−x kleiner als ε ist.
Es gilt: U (a;ε) = {x∈R| a−ε < x < a+ε} bzw. {x∈R| |a−x| < ε}.
Die ε-Umgebung U (a;ε) ist also das offene Intervall (a−ε;a+ε).
Def. (Grenzwert einer Folge)
Die Zahl a heißt Grenzwert der Folge (an), falls ∀ ε > 0 eine natürliche Zahl N existiert, so
dass an ∈ U(a;ε) ∀ n ≥ N, d.h. in jeder ε-Umgebung von a liegen alle Glieder der Folge ab
dem N. Glied. Daher bezeichnet man ε als die Fehlertoleranz.
Eine Folge mit dem Grenzwert 0 wird als Nullfolge bezeichnet.
Besitzt eine Folge einen Grenzwert, so wird sie als konvergent, andernfalls als divergent
bezeichnet.
Folgen, deren Folgenglieder sich konsequent +∞ oder -∞ nähern, nennt man bestimmt
divergent.
Satz (Nullfolge)
Jede Folge, bei der die Variable n ausschließlich im Nenner vorkommt, ist eine Nullfolge.
Satz (Vergleichskriterium)
Sei k ∈ !N und (an), (bn), (cn) reellwertige Folgen mit an ≤ bn ≤ cn für alle n ≥ k. Dann folgt aus
der Konvergenz von (an) und (cn) gegen den gleichen Grenzwert g die Konvergenz von (bn)
gegen diesen Grenzwert.
Satz (Grenzwertsatz)
Sind (an) und (bn) konvergente Folgen mit den Grenzwerten a bzw. b, dann sind die Folgen
(an)+(bn), (an)-(bn), (an)*(bn) und (an)/(bn) (für (bn) ≠ 0) ebenso konvergent und haben die
Grenzwerte a+b, a-b, a*b und a/b (für b ≠ 0).
Satz (Konvergenzkriterium)
Jede monoton wachsende und nach oben beschränkte Folge ist konvergent, d.h. an ≤ an+1 und
an ≤ A ∀ n ∈ N impliziert (an) konvergiert und der Grenzwert ist kleiner gleich der oberen
Schranke A.
Hinweis: Dieses Kriterium kann zum Nachweis der Konvergenz, aber auch zum Nachweis der
Divergenz verwendet werden.
Def. (Grenzwert einer reellen Funktion gegen unendlich)
Eine Zahl A ∈ !R heisst Grenzwert einer Funktion f: !R → !R für x gegen unendlich, falls
∀ bestimmt divergenten Folgen (xn) mit xn → ∞ für n → ∞ gilt: Die Folge f(xn) hat den
Grenzwert A.
Der Grenzwert gegen -∞ ist analog definiert.