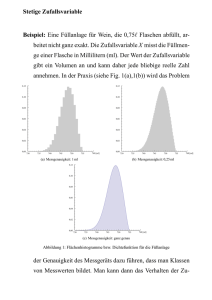
6.4 Hypergeometrische Verteilung
Werbung

6.6 Poisson-Verteilung Die Poisson-Verteilung ist eine Wahrscheinlichkeitsverteilung, die zur Modellierung der Anzahl von zufälligen Vorkommnissen in einem bestimmten räumlichen oder zeitlichen Abschnitt verwendet werden kann. Dabei wird unterstellt, dass die im Mittel erwartete Anzahl in gleichgroßen Abschnitten gleich ist. Beispiel 6.10: Beispiele für Fragestellungen, in denen die Poisson-Verteilung von Bedeutung ist, sind: - Unfälle in einer Fabrik pro Tag, Telefonanrufe in einer Vermittlungsstelle während einer Stunde, Basisinnovationen in einer Branche pro Jahr, tödliche Betriebsunfälle in einer Periode, Ankünfte von Flugzeugen auf einem Flughafen pro Minute, Druckfehler auf einer Buchseite, Anzahl von notwendigen Bombenentschärfungen je Quadratkilometer. 43 Eine Zufallsvariable X folgt einer Poisson-Verteilung mit dem Parameter λ , wenn die Wahrscheinlichkeitsfunktion von X durch (6.24) x x 0,1, e x ! f x 0 sonst mit λ >0 gegeben ist. Erwartungswert und Varianz der Poisson-Verteilung Erwartungswert (6.26) E(X) = λ Varianz (6.27) V(X) = λ Erwartungswert und Varianz stimmen also überein. 44 Wir illustrieren die Rolle des Parameters λ bei der Poisson-Verteilung anhand zweier Stabdiagramme. f (x) f (x) 0,6 0,3 0,4 0,2 0,2 0,1 0 a) λ = 0,5 1 2 3 4 5 6 x 0 1 2 3 4 5 6 x b) λ = 2 Die Wahrscheinlichkeitsfunktion der Poisson-Verteilung verläuft linkssteil (rechtsschief). Mit zunehmendem Wert des Parameters λ nehmen die Wahrscheinlichkeiten größerer x-Werte zu. Während der Modus bei kleinem λ gleich 0 ist, steigen die Wahrscheinlichkeiten bei größerem λ erst einmal an, ehe sie ihr Maximum erreichen. Man kann die Poisson-Verteilung auch als Rechenvereinfachung für die Binomialverteilung verwenden: Mit p 0,1 und n 50 (Faustregel) lassen sich Wahrscheinlichkeiten bei binomialverteilten Zufallsvariablen approximativ durch Poisson-verteilte Zufallsvariablen mit λ = np berechnen. 45 Bezug zur Binomialverteilung (hier: Zeitabschnitt): Wir zerlegen den Zeitabschnitt [0,t] in n gleich lange Teilintervalle. Diese n Teilintervalle haben dann alle die Länge t/n: t/n 0 t/n ... t/n t Wir unterstellen, dass n groß genug gewählt wurde, so dass Folgendes gilt: - In jedem der n Teilintervalle kann das betrachtete Vorkommnis entweder einmal (Ereignis A) oder keinmal auftreten (Ereignis A ). Die Wahrscheinlichkeit, dass das Vorkommnis in einem Teilintervall mehr als einmal auftritt, ist vernachlässigbar klein. Also liegt in jedem Teilintervall ein Bernoulli-Experiment vor. - Das Eintreten von A im i-ten Teilintervall ist unabhängig vom Eintreten von A im j-ten Teilintervall (i ≠ j), d. h. bei in jedem Teilintervall tritt A mit der Wahrscheinlichkeit p ein. Also liegt insgesamt ein endlicher Bernoulli-Prozess vor. Unter diesen Annahmen ist die Anzahl X des Eintretens des Ereignisses A (und damit die Anzahl des betrachteten Vorkommnisses) im Gesamt-Zeitabschnitt binomialverteilt mit den Parametern n und p und dem Erwartungswert E(X) = n p. Dabei ergibt sich typischerweise eine sehr große Zahl n von Teilintervallen, in denen in sehr vielen Fällen das Ereignis A eintritt, d. h. die Wahrscheinlichkeit p wird sehr klein (und damit 1 – p ≈ 1). Daher bezeichnet man die Poisson-Verteilung auch als die „Verteilung seltener Ereignisse“, und zwar selbst dann, wenn das 46 betrachtete Vorkommnis im Gesamt-Zeitabschnitt gar nicht so selten auftritt. Beispiel 6.10: Die Wahrscheinlichkeit, dass eine Person ein bestimmtes Medikament nicht verträgt, sei 0,001. Insgesamt wurden 2.000 Personen mit diesem Medikament behandelt. Dann ist die Anzahl der mit dem Medikament behandelten Personen, die das Medikament nicht vertragen, binomialverteilt mit den Parametern n = 2000 und p = 0,001, so dass die Wahrscheinlichkeiten aus 2000 PX x 0,001x 0,9992000 x x ermittelt werden können. Die Berechnung mit dieser Formel ist jedoch umständlich. Da die Faustregel für die Approximation durch die Poisson-Verteilung hier erfüllt ist, (p = 0,001) < 0,1 und (n = 2000 > 50, können wir das betrachtete Ereignis, das Medikament nicht zu vertragen, näherungsweise als Poisson-verteilt betrachten. Mit dem Parameter λ = n·p = 2000·0,001 = 2 erhält man die zu verwendende Wahrscheinlichkeitsfunktion der Poisson-Verteilung 2x 2 x 0,1, e f x x! . 0 sonst 47 Mit der Wahrscheinlichkeitsfunktion der Poisson-Verteilung erhält man z. B. 20 2 PX 0 f 0 e e2 0,1353 0! und 21 2 PX 1 f 1 e 2 e2 0,2707. 1! Insgesamt ergibt der Vergleich zwischen Binomialverteilung und Poisson-Verteilung nur geringe Abweichungen, die ab der vierten Dezimalstelle bestehen Binomialverteilung Poisson-Verteilung P(X=0) 0,1352 0,1353 P(X=1) 0,2707 0,2707 P(X=2) 0,2708 0,2707 P(X=3) 0,1805 0,1804 P(X=4) 0,0902 0,0902 ♦ 48 Beispiel 6.11: Eine Versicherung hat für einen Zeitraum von einem Jahr in 200 Bauunternehmen 122 schwere Unfälle bei Hochbauarbeiten ermittelt. Wie groß ist die Wahrscheinlichkeit, dass es in einem Bauunternehmen in einem Jahr zu 0, 1, 2 und mehr als 2 schweren Unfällen bei Hochbauarbeiten kommt? Wir betrachten das einzelne Unternehmen als “räumlichen” Abschnitt und nehmen an, dass die im Mittel erwartete Anzahl der Unfälle für gleichgroße Abschnitte (d. h. für dieses oder andere einzelne Unternehmen) gleich groß ist, so dass die gesuchen Wahrscheinlichkeiten mit der Poissonverteilung berechnet werden können. Hierzu muss der Parameter λ festgelegt werden, der den Erwartungswert für die Anzahl der schweren Unfälle in einem Bauunternehmen pro Jahr angibt. Unter Ausnutzung der verfügbaren Informationen verwenden wir für den Parameter λ die durchschnittliche Zahl der schweren Unfälle bei allen Unternehmen: λ = 122 / 200 = 0,61. 49 Zur Bestimmung der gesuchten Wahrscheinlichkeiten betrachten wir daher folgende Wahrscheinlichkeitsfunktion für die Anzahl X der schweren Unfälle bei Hochbauarbeiten: 0,61x -0,61 x = 0, 1, … x! e f x = 0 sonst Daraus ergeben sich folgende Wahrscheinlichkeiten: 0,610 -0,61 P X = 0 = f 0 = e = e-0,61 = 0,5434 0! 0,611 -0,61 P X = 1 = f 1 = e = 0,61e-0,61 = 0,3314 1! 0,612 -0,61 P X = 2 = f 2 = e = 0,18605e-0,61 = 0,1011 2! P X > 2 = 1 - P(X 2) = 1 - [f(0) + f(1) + f 2 ] = 1 - (0,5434 + 0,3314 + 0,1011) = 1 - 0,9759 = 0,0241 50 6.7 Normalverteilung Die Normalverteilung kann als das wichtigste Verteilungsmodell der Statistik angesehen werden. Sie wird nach ihrem Entdecker auch Gaußsche Glockenkurve genannt. Die herausragende Stellung der Normalverteilung in der Statistik erklärt sich aus drei Gründen: ● Bestimmte Zufallsvariablen sind „von Natur aus“ normalverteilt. - naturwissenschaftliche Variablen: z.B. Intelligenz, Körpergröße, Messfehler - wirtschafts- und sozialwissenschaftliche Variablen: in machen Fällen nach einer log-Transformation (d . h. nach Logarithmus-Berechnung aller Werte) approximativ normalverteilt (z.B. Einkommen) ● Die Normalverteilung ist bei großem n die Grenzverteilung anderer Verteilungen ● Unter sehr allgemeinen Bedingungen sind Summen und Durchschnitte unabhängiger Zufallsvariablen näherungsweise normalverteilt ( Zentraler Grenzwertsatz). Diese Eigenschaft ist insbesondere in der induktiven Statistik von herausragender Bedeutung 51 Eine Zufallsvariable X heißt normalverteilt mit den Parametern µ und σ2, X ~ N(µ, σ2), wenn ihre Dichtefunktion durch (6.28) f x 1 e 2 1 x 2 2 , x gegeben ist. Abbildung: Dichtefunktion einer normalverteilten Zufallsvariablen f (x) X ~ N ; 2 π = 3,14159… (Kreiskonstante) e = 2,71828… (Eulersche Zahl) µ x 52 Diskussion der Dichtefunktion 1. Die Dichtefunktion f(x) ergibt sich durch die Multiplikation der e-Funktion e 1 x 2 2 mit dem konstanten Faktor 1 ( 2) . Aus 1 x e 2 2 dx 2 folgt, dass der konstante Faktor ausschließlich aus Normierungsgründen verwendet wird: Die Fläche unterhalb der Dichtefunktion muss gleich 1 sein. 1 x 2 2 bewirkt, 2. Das negative Vorzeichen des Exponenten der e-Funktion e dass die Funktionswerte mit wachsendem Abstand von μ kleiner werden, die Dichtefunktion also zu den Rändern hin abnimmt. Diese Abnahme ist zu beiden Seiten gleich, was durch die Quadrierung im Exponenten gewährleistet wird. Aufgrund der Quadrierung ist die Verteilung symmetrisch um den Parameter µ, der zugleich der Erwartungswert ist: f(µ-x) = f(µ+x) für alle x . 53 3. Der Exponent der e-Funktion e 1 x 2 2 ist für alle x ≠ μ negativ und nimmt den maximalen Wert 0 für x = μ an. Die Verteilung ist daher unimodal. Wegen e0 = 1 für x = μ ist das Maximum der Dichtefunktion ist durch den konstanten Faktor 1 ( 2 ) gegeben: 1 maxf x f . 2 4. Je kleiner der Streuungsparameter σ ist, desto größer ist der absolute Wert des Exponenten der e-Funktion e 1 x 2 2 für einen gegebenen Abstand x – μ, d.h. desto rascher fällt die Dichtefunktion ab. Außerdem wird bei fallendem σ der Nenner des konstanten Faktors kleiner, 1 ( 2 ) , d.h. das Maximum der Dichtefunktion steigt. Je kleiner also σ ist, um so steiler verläuft die Dichtefunktion der Normalverteilung um das Symmetriezentrum µ. 54 Bedeutung der Parameter µ und σ2 der Normalverteilung f(x) 1 2 3 Wenn der Erwartungswert µ steigt, dann verschiebt sich die Dichtefunktion nach rechts. x 1 2 3 f(x) 12 22 32 12 Wenn die Varianz σ2 sinkt, verläuft die Dichtefunktion steiler um den Erwartungs-wert µ. 22 32 x 55







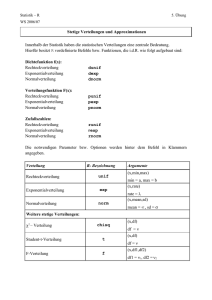




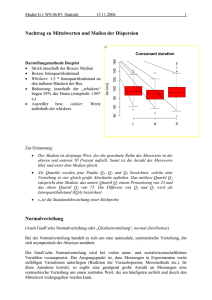

![E[g(X)]](http://s1.studylibde.com/store/data/002437238_1-904729117acad3aaef2cefc6444782e9-300x300.png)