KAPITEL VII GRAVITATION

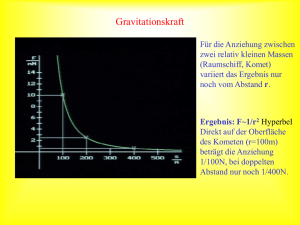
KAPITEL VII
GRAVITATION
1. KRAFTFELDER
Die experimentellen Erfahrungen haben gezeigt, dass Körper anscheinend auf zwei verschiedene
Weisen Kräfte aufeinander ausüben können, und zwar
• durch die Vermittlung mehr oder weniger starrer Verbindungen,
• ohne jeden erkennbaren Übertragungsmechanismus durch den leeren Raum hindurch.
FARADAY nahm an, dass die Anwesenheit eines elektrisch geladenen Körpers oder eines Magnets in
dem umgebenden Raum gewisse Veränderungen verursacht, auch wenn dieser völlig leer ist.
Diese Veränderungen des Raumes üben dann auf einen zweiten Körper bestimmte Wirkungen aus.
Damit werden dem leeren Raum physikalische Eigenschaften zugeschrieben, die ihn befähigen, auf
Körper Kräfte auszuüben. Wir setzen fest :
Unter einem Kraftfeld oder einem Feld versteht der Physiker einen mit bestimmten
physikalischen Eigenschaften ausgestatteten Raum, in dem auf Körper mit den entsprechenden,
für das Feld charakteristischen physikalischen Eigenschaften Kräfte und Drehmomente ausgeübt
werden.
Die Kraftfelder spielen in der Physik eine große Rolle. Wir unterscheiden vor allem die vier
folgenden Arten von Kraftfeldern :
• In der Umgebung eines Magneten oder eines stromdurchflossenen Leiterstückes ist ein
magnetisches Feld vorhanden. In jedem seiner Punkte wird auf einen anderen Magneten
ein Drehmoment ausgeübt.
• In der Umgebung einer elektrischen Ladung befindet sich ein elektrisches Feld, durch das
auf eine andere elektrische Ladung innerhalb dieses Feldes eine Kraft ausgeübt wird.
• In der Umgebung eines materiellen Körpers befindet sich das Schwere- oder
Gravitationsfeld. In jedem Raumpunkt wird auf einen anderen materiellen Körper eine
Kraft ausgeübt, die ihre Ursache in dem Vorhandensein des ersten Körpers hat.
• Im Bereich der Atomkerne wirkt das Kernfeld. Dieses ist für die Übertragung der Kräfte
zwischen den Kernbausteinen verantwortlich.
GRAVITATION 2
2. PLANETENBEWEGUNG
2.1 GEOZENTRISCHES WELTBILD
Man hat sich bereits im Altertum bemüht, eine Erklärung für die Bewegung der Himmelkörper zu
geben und die zugrunde liegenden Gesetze aufzufinden. Das gesamte astronomische Wissen jener
Zeit wurde von CL. PTOLEMÄUS (85 – 165 n. Chr.) in dem Buche Almagest zusammengefasst.
Dieses Buch blieb 1400 Jahre für die Himmelskunde maßgebend. Der Lehre des Ptolemäus liegen
folgende beide Annahmen zugrunde :
• Die Erde steht im Mittelpunkt der Welt.
• Die Himmelskörper bewegen sich mit konstanten Bahngeschwindigkeiten auf kreisförmigen
Bahnen.
Diese beiden Grundannahmen sind durch die Astronomen des Altertums einmal aus den
Beobachtungen der täglichen Gestirnbewegungen, die den Eindruck erwecken, als ob die Erde
ruhend im Mittelpunkt der Welt stünde, abgeleitet worden. Zum anderen sind sie aber auch ein
Ausdruck mythischer Vorstellungen, nach denen man in den Himmelskörpern göttliche Wesen sah,
denen nur die vollkommenste aller Bewegungen angemessen sein sollte. Als vollkommenste
Bewegung betrachtete man damals die Kreisbewegung.
Wenn nun bei bestimmten Himmelskörpern, wie den Planeten, Abweichungen von der Kreisbahn
beobachtet wurden, so kombinierte man mehrere Kreisbewegungen miteinander, indem man sich
vorstellte, dass der Planet P eine kreisförmige Bahn um einen gewissen Punkt beschreibt, der sich
seinerseits wieder auf einer Kreisbahn um die Erde E bewegt. Die so entstandenen Kurven
bezeichnet man als Epizykloiden.
2.2 HELIOZENTRISCHES WELTBILD
Eine neue Vorstellung der Planetenbewegungen bahnte sich an, als N. KOPERNIKUS (1473-1543) im
Jahre 1543 sein Werk „De revolutionibus orbium coelestium“ veröffentlichte. Der grundlegende
Unterschied gegenüber der Lehre von Ptolemäus besteht darin, dass die Erde ihre bevorzugte
Stellung als ruhender Mittelpunkt der Welt verliert und sich ebenso wie die anderen Planeten um
die Sonne bewegt. Der Lehre des Kopernikus liegen die beiden folgenden Annahmen zugrunde :
• Die Erde dreht sich täglich einmal um ihre eigene Achse.
• Die Erde und die Planeten bewegen sich auf Kreisbahnen um die Sonne.
Man bezeichnet die Lehre von Kopernikus nach der die Sonne der Mittelpunkt der Welt und
insbesondere des Planetensystems sein sollte als heliozentrisches Weltbild.
Aber auch Kopernikus selbst konnte sich noch nicht völlig von den überlieferten Anschauungen frei
machen. Er hielt nach wie vor an der Vorstellung fest, dass allein die Kreisbewegung als die
vollkommenste Bewegung für die Himmelskörper in Frage kommt.
GRAVITATION 3
Durch J. KEPLER (1571-1630) wurde die Lehre von Kopernikus zur allgemeinen Anerkennung
gebracht. Sich auf das umfangreiche Beobachtungsmaterial von T. BRAHE stützend, konnte Kepler
nachweisen, dass die Planeten sich nicht auf Kreisen um die Sonne bewegen. Schließlich fand
Kepler nach sechsjährigen Berechnungen die drei folgenden nach ihm benannten Gesetze.
2.3 1. KEPLER-GESETZ
Die Planeten bewegen sich auf Ellipsen, die einen gemeinsamen Brennpunkt haben, in dem die
Sonne steht.
Die Ellipse ist die Menge aller Punkte P mit der Eigenschaft
PF1 + PF2 = const., dabei sind die Punkte F1 und F2 die Brennpunkte
der Ellipse. Die Strecke MA=MB ist die große Halbachse a der
Ellipse; MC=MD entsprechend die kleine Halbachse b. Unter der
linearen Exzentrizität versteht man die Längen F1M=F2M=e,
während die numerische Exzentrizität ε der Quotient aus e und a
ist. Für ellipsenförmige Bahnen liegt ε zwischen 0 und 1. Für ε = 0
ist e = 0 und damit F1 = F2 = M. Die Bahn ist dann ein Kreis. Die
Bahnen von Venus, Neptun und Erde weichen nur sehr wenig von
der Kreisbahn ab (ε < 2%), während die Bahnen von Merkur und
Pluto ausgeprägte Ellipsen sind (ε > 20%).
2.4 2. KEPLER-GESETZ
Der Radiusvektor, das heißt die Verbindungslinie Sonne-Planet, überstreicht in gleichen Zeiten
gleich große Flächen.
Das 2. Kepler-Gesetz wird auch als Flächensatz bezeichnet.
Wenn man die an verschiedenen Stellen der Planetenbahn in
einem bestimmten Zeitintervall Δt zurückgelegten Wege Δs1,
Δs2 und Δs3 ermittelt, so zeigt sich, dass diese verschieden
lang sind; sie sind so beschaffen, dass die entsprechenden
Flächen ΔA1, ΔA2 und ΔA3 gleich sind. Man bezeichnet den
sonnen-nächsten Punkt eines Planeten auf seiner
elliptischen Bahn als Perihel und den sonnenfernsten Punkt
als Aphel. Die Erde erreicht den sonnennächsten Punkt
Anfang Januar und den sonnenfernsten Punkt im Juli.
Der Flächensatz, der von Kepler aus den Beobachtungen der Planetenbewegungen entwickelt
worden ist, stellt nicht anderes als den uns bekannten Drehimpulserhaltungssatz dar. Um
diesen Zusammenhang zu erkennen, betrachten wir einen Massenpunkt mit der Masse m , der sich
zunächst in einem Punkt P1 in der Nähe des Perihel befindet. Er bewegt sich in dem Zeitintervall Δt
mit der Winkelgeschwindigkeit ω1 nach Q1, wobei der Radiusvektor den Winkel Δϕ1 überstreicht.
Nach einiger Zeit befindet sich der Massenpunkt in der Nähe des Aphels im Punkt P2. Er bewegt
sich in dem Zeitintervall Δt mit der Winkelgeschwindigkeit ω2 nach Q2, wobei der Radiusvektor den
Winkel Δϕ2 überstreicht.
Nach dem Flächensatz von Kepler heißt es :
ΔA1 = ΔA2
Da allgemein für die vom Radiusvektor r überstrichene Fläche ΔA die Formel
ΔA =
1
2
⋅ r 2 ⋅ Δϕ
1
2
⋅ r22 ⋅ Δϕ 2
gilt, ergibt sich
1
2
⋅ r12 ⋅ Δϕ1
=
GRAVITATION 4
r12 ⋅ Δϕ1
m ⋅ r12 ⋅
= r22 ⋅ Δϕ 2
Δϕ1
Δt
= m ⋅ r22 ⋅
⋅
m
Δt
Δϕ 2
Δt
Aufgrund früherer Ergebnisse gilt für die Trägheitsmomente
J1
= m ⋅ r12
und
J2
= m ⋅ r22
ω2
=
und für die Winkelgeschwindigkeiten
ω1 =
Δϕ1
Δt
und
Δϕ 2
.
Δt
Setzt man diese Ausdrücke oben ein, so erhält man
J 1 ⋅ ω1
=
J 2 ⋅ ω2
= L2
L1
wobei L1 und L2 die Drehimpulse des Massenpunktes m im Perihel und im Aphel darstellen.
Bemerkenswert ist dabei, dass diese Ableitung keine bestimmte Voraussetzung über die Größe der
wirkenden Kraft erfordert. Es genügt allein die Tatsache, dass die auf den bewegten Massenpunkt
ausgeübte Kraft stets auf ein bestimmtes Zentrum gerichtet ist. Der Flächensatz und der Satz der
Erhaltung des Drehimpulses gelten deshalb nicht nur für die Planetenbewegung, sondern für alle
Zentralbewegungen. Diese Bewegungen gehören zu den ungleichförmigen Bewegungen.
2.5 3. KEPLER-GESETZ
Die Quadrate der Umlaufzeiten T1 und T2 zweier Planeten verhalten sich wie die dritten
Potenzen der großen Halbachsen a1 und a2 der Bahnellipsen.
T12
T22
=
a13
a 23
oder
T12
a13
=
T22
a 23
= k
Die Konstante k hat also für alle Planeten des Sonnensystems den gleichen Wert. Man kann
diesen Wert berechnen, indem man die Umlaufzeit T und die Länge der großen Halbachse a für
irgendeinen Planeten einsetzt. Aus den Werten der Erde ergibt sich für unser Sonnensystem
k
T2
=
a3
T
= 1 a = 365,25 d
= 3,16 ⋅ 10 7 s
a = 1,50 ⋅ 1011 m
(3,16 ⋅ 10 )
(1,50 ⋅10 )
7 2
k
=
k
= 2,95 ⋅ 10 −19 s 2 m −3
11 3
Für ein anderes Planetensystem, das anstatt der Sonne ein Zentralgestirn mit anderer Masse
besitzt, ergibt sich ein anderer Wert der Konstanten k .
Das 3. Kepler-Gesetz gilt auch für die Bewegung künstlicher Satelliten um die Erde. Auch hier
gehört zu jeder Umlaufzeit T ein ganz bestimmter Bahnradius r bzw. eine ganz bestimmte große
Halbachse a. Es ist daher unmöglich bei einem Satelliten die Umlaufzeit als auch den Bahnradius
bzw. die große Halbachse willkürlich zu wählen. Wenn man das eine Bestimmungsstück frei
gewählt hat, dann ist das andere damit zwangsläufig gegeben.
GRAVITATION 5
3. NEWTONSCHES GRAVITATIONSGESETZ
Obwohl die Kepler-Gesetze die Bewegung der Planeten richtig wiedergeben, machen sie keine
Aussage über die für das Zustandekommen der Planetenbewegung erforderlichen Kräfte. Newton
hat als erster erkannt, dass die Kraft, die für das Fallen eines Apfels zur Erde verantwortlich ist,
auch den Mond auf seine bahn um die Erde und die Planeten auf ihre Bahnen um die Sonne
zwingt und dass wir es schließlich bei der Anziehung, die zwei beliebige Massen aufeinander
ausüben, ebenfalls mit der gleichen Kraft, der Gravitationskraft, zu tun haben.
Zur Berechnung der Gravitationskraft stützte Newton sich auf die Zentripetalkraft, die drei
Keplerschen Gesetze und das von ihm entdeckte Wechselwirkungsgesetz „actio=reactio“. In
Abweichung zu den Kepler-Gesetzen nahm Newton vereinfachend an :
- Die Planeten bewegen sich auf Kreisbahnen.
- Auf diesen Kreisbahnen bewegen sich die Planeten mit gleich bleibender Geschwindigkeit.
Zunächst berechnete er die Zentripetalkraft, die nötig ist um einen Planeten auf seiner Bahn zu
halten:
FZ
= m ⋅ω 2 ⋅ r
FZ
=
FZ
=
FZ
=
FZ
=
ω=
4π 2
⋅m⋅r
T2
4π 2
⋅m⋅r
k ⋅ r3
4π 2
⋅m
k ⋅r2
4π 2 m
⋅
k r2
2π
T
3. Kepler − Gesetz → T 2 = k ⋅ r 3
Aus dieser Gleichung folgt: Die Gravitationskraft ist der Masse m des Planeten direkt und dem
Quadrat seines Abstandes von der Sonne umgekehrt proportional. Als Proportionalität erhält man
F
~
m
r2
[A]
Hieran schloss Newton einen neuen Gedanken an: Alle Körper ziehen sich aufgrund ihrer Masse
gegenseitig an. Wenn also die Sonne mit der Masse M auf einen Planeten mit der Masse m die
Gravitationskraft FS ausübt, muss auch der Planet auf die Sonne die Gravitationskraft FPl
ausüben. Die Proportionalität [A] erhält dann für beide Gravitationskräfte die symmetrischen
Ausdrücke
FS
~
m
r2
[B]
und
FPl
~
M
r2
[C]
Nun zog Newton zusätzlich das Wechselwirkungsgesetz heran, nach dem die beiden Gravitationskräfte FS und FPl gleich groß sind. Demnach lassen sich die beiden Proportionalitäten [B] und [C]
vereinen zu
F
~
M ⋅m
r2
GRAVITATION 6
Unter Einfügung einer Proportionalitätsfaktors ergibt sich schließlich das Gravitationsgesetz
F
= G⋅
M ⋅m
r2
Darin bedeuten M die Masse der Sonne, m die Masse des Planeten und r der Abstand zwischen
den Mittelpunkten beider Himmelskörper.
Die Proportionalitätskonstante G heißt Gravitationskonstante. G ist eine Naturkonstante, sie
hat stets und überall den gleichen Wert
G = 6,67‚10-11 m3‚kg-1‚s-2
Wenn man das Gravitationsgesetz nicht auf die Bewegung der Planeten um die Sonne anwendet,
sondern die Gravitation zwischen zwei beliebigen Körpern mit den Massen m1 und m2
untersucht, dann schreibt sich das Gravitationsgesetz allgemein :
F
= G⋅
m1 ⋅ m 2
r2
GRAVITATION 7
4. GRAVITATIONSFELD
4.1 GRAVITATIONSFELD DER ERDE
In der Gleichung für die Gravitationskräfte gehen beide Massen m1 und m2 in völlig symmetrischer Weise ein. Man kann sich aber auch auf einen anderen Standpunkt stellen. Dieser ist dann
nützlich, wenn die Masse des einen Körper (zum Beispiel der Erde) gegenüber der Masse des
zweiten Körpers (zum Beispiel des Apfels am Baum) so groß ist, dass von den zwei
entgegengesetzt gerichteten und gleich großen Kräften nur eine Gravitationswirkung (der Fall des
Apfels) beobachtbar ist, während die zweite Wirkung (der Fall der Erde zum Apfel) nur eine
theoretische Erörterung darstellt.
Diesen Standpunkt nehmen wir jetzt für die Erde an. Dann können wir an jeder Stelle im erdnahen
Raum des Weltalls die Gravitationskraft der Erde auf einen Körper nachweisen. Einen Raum mit
solchen Eigenschaften nennt man in der Physik ein Kraftfeld oder Feld. Da die Kraft allein
aufgrund der Masse des in dieses Feld gebrachten Körper ausgeübt wird, nennt man dieses Feld
Gravitationsfeld.
Die Gravitationskraft
= G⋅
F
der Erde auf
abhängig :
-
mE ⋅ m
r2
Körper der Masse m in ihrem Gravitationsfeld ist von drei physikalischen Größen
der felderzeugenden Masse mE der Erde,
der Masse m des Köpers im Feld,
dem Abstand r des Körpers zum Erdmittelpunkt.
Die Gleichung für die Gravitationskraft enthält also einerseits Größen, die zur Erde und damit zum
Gravitationsfeld gehören, andererseits die Größe m , die zum Körper im Feld gehört.
mE F
beschreibt dabei mathematisch die Eigenschaften eines von der Masse
=
m
r2
mE erzeugten Gravitationsfeldes am Ort mit dem Abstand r zum Erdmittelpunkt. Man bezeichnet
diesen Ausdruck als Gravitationsfeldstärke g .
Der Ausdruck G ⋅
Die Gravitationsfeldstärke g an einem bestimmten Ort des Gravitationsfeldes ist der Quotient
aus der Gravitationskraft F, die ein Körper aufgrund seiner Masse an diesem Ort erfährt, und
seiner Masse m .
g
=
F
m
= G⋅
mE
r2
Die Einheit der Gravitationsfeldstärke ist N/kg.
Die Richtung der Gravitationsfeldstärke entspricht der Richtung der Kraft auf den Körper.
Kennt man an einem Ort im Gravitationsfeld die Gravitationsfeldstärke g , so kann man die an
diesem Ort auf einen Körper mit der Masse m ausgeübte Gravitationskraft F berechnen mit
F
= m⋅ g
Diese Gleichung erinnert an die Gleichung für die Gewichtskraft G . Die Gravitationsfeldstärke g
der Erde und die Schwerebeschleunigung g der Erde stimmen in ihren Beträgen überein.
GRAVITATION 8
Sie werden entsprechend ihren unterschiedlichen physikalischen Bedeutungen nur in verschiedenen Einheiten angegeben. So beträgt die Gravitationsfeldstärke in den geografischen Breiten
Mitteleuropas 9,81 N‚kg-1, während die Schwerebeschleunigung 9,81 m‚s-2 beträgt.
Zur Veranschaulichung des Gravitationsfeldes benutzt man Feldlinien. Als Richtung der Feldlinien
wählt man die Richtung der Gravitationsfeldstärke. Das Gravitationsfeld der Erde ist annährend
kugelsymmetrisch. In zweidimensionaler Darstellung erscheint es als Radialfeld.
4.2 POTENTIELLE ENERGIE IM GRAVITATIONSFELD
Die im Kapitel III aufgestellte Formel für die potentielle Energie E POT = m ⋅ g ⋅ h setzt voraus, dass
die Gravitationskraft konstant ist. Dies ist in der Nähe der Erdoberfläche annährend gegeben.
Beschränken wir das Anheben eines Probekörpers jedoch nicht mehr auf erdnahe Bereiche,
sondern weiten es auf große Höhen aus, kann die Gravitationskraft nicht mehr als konstant gelten.
Für die auf einen Probekörper mit der Masse m0
Gravitationsgesetz von Newton
F
= G⋅
wirkende Gravitationskraft gilt dann das
m E ⋅ m0
r2
Zum Heben des Probekörper muss gegen diese von dem Abstand r
abhängende Kraft Energie aufgebracht werden.
zum Erdmittelpunkt
Der Probekörper möge sich zunächst auf der Erdoberfläche befinden und
vom Zentrum der Erde den Abstand rE haben. Er soll in der Vertikalen, also
parallel zu den Feldlinien, nach oben bewegt werden, bis er vom Erdmittelpunkt den Abstand r besitzt. Um die für diese Anheben erforderliche Energie
zu berechnen, denkt man sich den Gesamtweg in eine große Anzahl kleinerer
Wegintervalle Δr zerlegt, die so beschaffen sind, dass die Gravitationskraft
für jedes dieser Intervalle als konstant betrachtet werden kann.
Für das erste von rE nach r1 reichende Intervall beträgt die Gravitationskraft
am Anfang der Intervalls
FA
= G⋅
m E ⋅ m0
rE2
am Ende des Intervalls
FE
= G⋅
m E ⋅ m0
.
r12
GRAVITATION 9
Man verwendet nun einen Mittelwert, indem man als mittlere Entfernung ri
Mittel von rE und r1 einsetzt :
ri
=
das geometrische
rE ⋅ r1 .
Dann ergibt sich für die mittlere Gravitationskraft im ersten Intervall
FE
= G⋅
m E ⋅ m0
ri 2
= G⋅
m E ⋅ m0
.
rE ⋅ r1
Dieser Mittelwert kann für das ganze erste Intervall als konstant angesehen werden, so dass zum
Anheben des Körpers im ersten Intervall die Energie E1 aufgebracht werden muss mit
E1
= F1 ⋅ (r1 − rE ) = G ⋅
⎛ 1 1⎞
m E ⋅ m0
⋅ (r1 − rE ) = G ⋅ m E ⋅ m0 ⋅ ⎜⎜ − ⎟⎟ .
rE ⋅ r1
⎝ rE r1 ⎠
In analoger Weise ergibt sich für die als konstant zu betrachtende mittlere Gravitationskraft F2 des
zweiten, von r1 bis r2 reichenden Intervalls
F2
= G⋅
m E ⋅ m0
.
r1 ⋅ r2
Die in diesem Intervall aufzuwendende Energie ist dann
E2
= F2 ⋅ (r2 − r1 ) = G ⋅
⎛1 1⎞
m E ⋅ m0
⋅ (r2 − r1 ) = G ⋅ m E ⋅ m0 ⋅ ⎜⎜ − ⎟⎟ .
r1 ⋅ r2
⎝ r1 r2 ⎠
Für ein drittes, von r2 bis r3 reichendes Intervall, erhält man entsprechend
E3
⎛1 1⎞
= G ⋅ m E ⋅ m0 ⋅ ⎜⎜ − ⎟⎟
⎝ r2 r3 ⎠
Diese Verfahren kann dann auf alle übrigen Intervalle ausgedehnt werden. Um die Gesamtenergie
zu bestimmen, die zum Anheben des Körpers bis auf den Abstand r erforderlich ist müssen alle
Teilenergien addiert werden. Dabei ergibt sich
E = E1 + E 2 + E3 + ... + E n −1 + E n
⎡⎛ 1 1 ⎞ ⎛ 1 1 ⎞ ⎛ 1 1 ⎞
⎛ 1
1 ⎞ ⎛⎜ 1
1 ⎞⎤
⎟⎟ +
E = G ⋅ m E ⋅ m0 ⋅ ⎢⎜⎜ − ⎟⎟ + ⎜⎜ − ⎟⎟ + ⎜⎜ − ⎟⎟ + ... + ⎜⎜
−
− ⎟⎥
⎜
⎟
⎢⎣⎝ rE r1 ⎠ ⎝ r1 r2 ⎠ ⎝ r2 r3 ⎠
⎝ rn −2 rn −1 ⎠ ⎝ rn −1 r ⎠⎥⎦
E
⎛1 1⎞
= G ⋅ m E ⋅ m0 ⋅ ⎜ − ⎟
⎜ rE r ⎟
⎝
⎠
Das hier gefundene Ergebnis gilt natürlich nicht nur für den Fall, dass die Erde die felderzeugende
Masse ist, sondern es handelt sich um eine für alle felderzeugenden Massen gültige Erkenntnis, die
allgemein so formuliert werden kann.
Um einen kleinen Probekörper der Masse m in einem von der kugelförmigen Masse M erzeugten
Gravitationsfeld gegen die Gewichtskraft von dem Punkt P1 mit dem Abstand r1 vom Zentrum der
felderzeugenden Masse – Zentralkörper – nach einem Punkt P2 mit dem Abstand r2 zu bringen,
muss die Energie
E1, 2
⎛1 1⎞
= G ⋅ M ⋅ m ⋅ ⎜⎜ − ⎟⎟
⎝ r1 r2 ⎠
aufgewendet werden.
GRAVITATION 10
Wird der Probekörper, z.B. ein Satellit, vom Zentralkörper, z.B. der Erde, wegbewegt (r2 > r1 ),
dann ist die Energie größer als Null und dem Gravitationsfeld wird Energie zugeführt. Umgekehrt
wird dem Gravitationsfeld Energie entzogen, wenn sich der Satellit der Erde nähert, denn nun gilt
r2 < r1 .
Diese Energie ist als potentielle Energie im Gravitationsfeld gespeichert.
Für die potentielle Energie EPOT kann der Ausgangspunkt oder Bezugspunkt P1 beliebig gewählt
werden. So könnte man im Fall des Erdfeldes die Erdoberfläche wählen mit r1 = rE = R. Es ist
aber üblich in der Physik für die potentiellen Energien in Kraftfeldern den Bezugspunkt P1 ins
Unendliche zu legen mit r1 → ∞ .
Die potentielle Energie eines Körpers der Masse m im radialen Gravitationsfeld eines Körpers
der Masse M ist in einem Punkt P (r ) gegenüber dem Bezugspunkt im Unendlichen
E POT ,r
= −
G⋅m⋅M
r
Im Unendlichen (r1 → ∞) ist die potentielle Energie EPOT,∞ = 0. Da dies der höchste Wert ist, den
die potentielle Energie im Kraftfeld annehmen kann, sind die potentiellen Energien aller endlichen
Abstände r stets negativ.
GRAVITATION 11