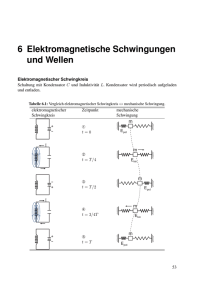
Der Amplitudenabfall einer gedämpften Schwingung ist vom

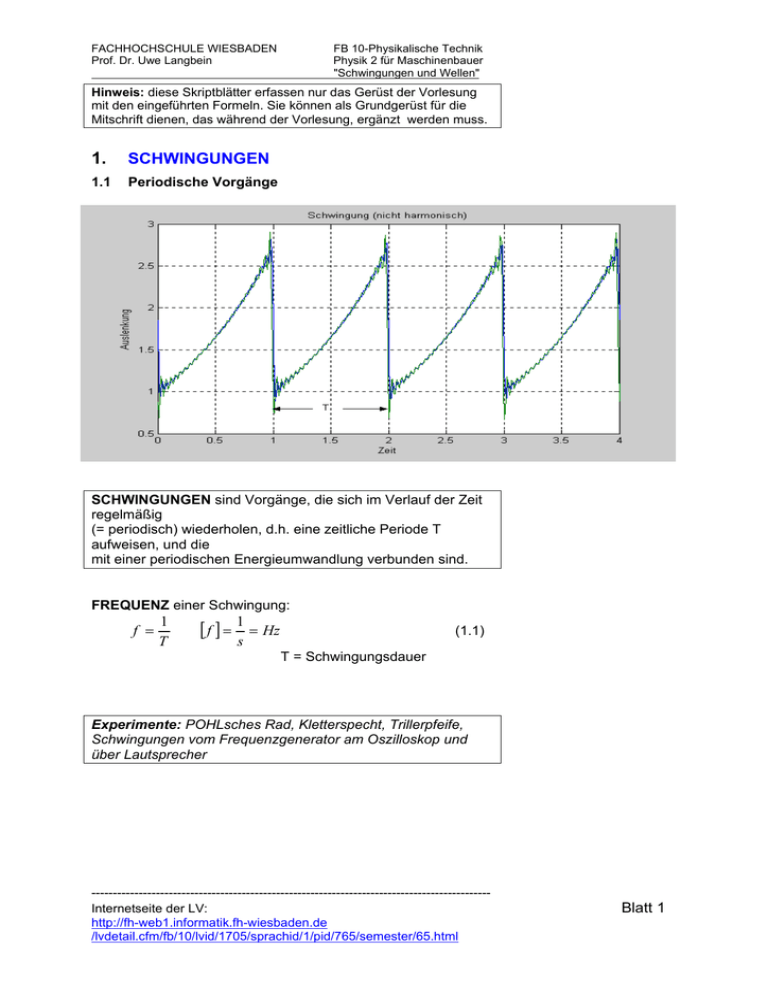
FACHHOCHSCHULE WIESBADEN
Prof. Dr. Uwe Langbein
FB 10-Physikalische Technik
Physik 2 für Maschinenbauer
"Schwingungen und Wellen"
Hinweis: diese Skriptblätter erfassen nur das Gerüst der Vorlesung
mit den eingeführten Formeln. Sie können als Grundgerüst für die
Mitschrift dienen, das während der Vorlesung, ergänzt werden muss.
1.
SCHWINGUNGEN
1.1
Periodische Vorgänge
SCHWINGUNGEN sind Vorgänge, die sich im Verlauf der Zeit
regelmäßig
(= periodisch) wiederholen, d.h. eine zeitliche Periode T
aufweisen, und die
mit einer periodischen Energieumwandlung verbunden sind.
FREQUENZ einer Schwingung:
f =
1
T
[ f ] = 1 = Hz
(1.1)
s
T = Schwingungsdauer
Experimente: POHLsches Rad, Kletterspecht, Trillerpfeife,
Schwingungen vom Frequenzgenerator am Oszilloskop und
über Lautsprecher
--------------------------------------------------------------------------------------------Internetseite der LV:
http://fh-web1.informatik.fh-wiesbaden.de
/lvdetail.cfm/fb/10/lvid/1705/sprachid/1/pid/765/semester/65.html
Blatt 1
FACHHOCHSCHULE WIESBADEN
Prof. Dr. Uwe Langbein
FB 10-Physikalische Technik
Physik 2 für Maschinenbauer
"Schwingungen und Wellen"
1.2 Ungedämpfte harmonische Schwingungen
1.2.1.1
Die Weg-Zeit-Funktion
Aus dem Vergleich der Bewegung eines Federschwingers und
der Projektion eines umlaufenden Zeigers lässt sich die Weg-
Zeit-Funktion einer harmonischen Schwingung bestimmen:
PHASENWINKEL ϕ = Drehwinkel des umlaufenden Zeigers
(im Bogenmass!):
ϕ = ϕ (t ) = ω ⋅ t
(1.2)
KREISFREQUENZ ω:
Weg-Zeit-Funktion:
ω = 2⋅π ⋅ f =
2π
T
(1.3)
y(t) = yˆ ⋅sin (ω⋅t)
(1.4)
y(t) = Auslenkung = ELONGATION
ŷ
= maximale Auslenkung = AMPLITUDE
Die (zeitabhängige) GESCHWINDIGKEIT einer Schwingung:
v=
dy
dt
= y&
v ( t ) = vˆ cos( ω ⋅ t ) = vˆ sin( ω ⋅ t +
(1.5)
π
2
) (1.6)
vˆ = maximale Geschwindigkeit:
vˆ = yˆ ⋅ ω
(1.6a)
--------------------------------------------------------------------------------------------Internetseite der LV:
http://fh-web1.informatik.fh-wiesbaden.de
/lvdetail.cfm/fb/10/lvid/1705/sprachid/1/pid/765/semester/65.html
Blatt 2
FACHHOCHSCHULE WIESBADEN
Prof. Dr. Uwe Langbein
FB 10-Physikalische Technik
Physik 2 für Maschinenbauer
"Schwingungen und Wellen"
Die (zeitabhängige) BESCHLEUNIGUNG einer Schwingung:
dv
d2y
a=
=
= &y&
dt
dt 2
a ( t ) = − aˆ ⋅ sin( ω ⋅ t ) = aˆ ⋅ sin( ω ⋅ t + π ) (1.7)
â = maximale Beschleunigung:
aˆ = vˆ ⋅ ω
(1.7a)
Ungedämpfte harmonische Schwingung:
Vergleich der Zeitfunktionen von Auslenkung y(t),
Geschwindigkeit v(t) und Beschleunigung a(t)
Auslenkung y(t):
Geschwindigkeit v(t)
Beschleunigung a(t)
--------------------------------------------------------------------------------------------Internetseite der LV:
http://fh-web1.informatik.fh-wiesbaden.de
/lvdetail.cfm/fb/10/lvid/1705/sprachid/1/pid/765/semester/65.html
Blatt 3
FACHHOCHSCHULE WIESBADEN
Prof. Dr. Uwe Langbein
FB 10-Physikalische Technik
Physik 2 für Maschinenbauer
"Schwingungen und Wellen"
Hinweis: Ist die Auslenkung einer Schwingung zur Zeit t = 0s
nicht null, müssen die Formeln (1.2) und (1.4) durch einen
NULLPHASENWINKEL ϕ0 ergänzt werden:
ϕ = ϕ(t) = ω ⋅ t +ϕ0
(1.2a)
y(t) = yˆ ⋅sin(ω⋅t +ϕ0 )
(1.4a)
Der Einfluß des Nullphasenwinkels auf die Weg-ZeitFunktion
--------------------------------------------------------------------------------------------Internetseite der LV:
http://fh-web1.informatik.fh-wiesbaden.de
/lvdetail.cfm/fb/10/lvid/1705/sprachid/1/pid/765/semester/65.html
Blatt 4
FACHHOCHSCHULE WIESBADEN
Prof. Dr. Uwe Langbein
FB 10-Physikalische Technik
Physik 2 für Maschinenbauer
"Schwingungen und Wellen"
1.2.2 Einfache schwingungsfähige Systeme:
1.2.2.1 Der ungedämpfte horizontale Federschwinger
D
D
D•y
Wirksame Kräfte:
FRück (t) = - D * y(t)
a) Federkraft:
(1.8)
D = Federkonstante
b) Trägheitskraft:
FTräg (t) = − m* a(t)
(1.9)
a(t)= Beschleunigung
c) Reibungskraft: Wird bei ungedämpft angenommenen Bewegungen
vernachlässigt.
Dynamisches Gleichgewicht:
FRück (t) + FTräg (t) = 0
d 2 y (t )
D
+
y (t ) = 0
2
m
dt
(1.10)
(1 . 11 )
Die Bewegungsgleichung (1.10) erlaubt, die Kreisfrequenz ω der
Schwingung aus den Eigenschaften des Schwingers zu ermitteln:
y ( t ) = yˆ ⋅ sin(ω t + ϕ 0 )
Die Weg-Zeit-Funktion
ist eine Lösung der Bewegungsgleichung (1.11), wenn gilt:
D
= ω0
m
ω=
f =
ω
1
=
2π 2π
(1.12)
D
= f0
m
(1.12a)
f0 = EIGENFREQUENZ des Federschwingers
T = 2π
m
= T0
D
(1.12b)
T0 = SCHWINGUNGSDAUER des Federschwingers
--------------------------------------------------------------------------------------------Internetseite der LV:
http://fh-web1.informatik.fh-wiesbaden.de
/lvdetail.cfm/fb/10/lvid/1705/sprachid/1/pid/765/semester/65.html
Blatt 5
FACHHOCHSCHULE WIESBADEN
Prof. Dr. Uwe Langbein
FB 10-Physikalische Technik
Physik 2 für Maschinenbauer
"Schwingungen und Wellen"
1.2.2.2 Das mathematische Pendel
= idealisiertes Pendel, weil:
•
•
•
gesamte Pendelmasse m im
Pendelkopf konzentriert
nur Ausschläge bis ca. 200 erlaubt
Reibung vernachlässigt
L = Pendellänge
β
m
s
FRück
β
s=l•β
(1.13)
r
G
s = Auslenkung auf Kreisbahn;
β = Auslenkungswinkel
Wesentliche Kräfte:
FRück = −G ⋅ sin β = −mg ⋅ sin β ≈ − mg ⋅ β (1.14)
FTrägh = − m ⋅ &s&
(1.15)
Kräftegleichgewicht: Frück + FTräg = 0 führt zur
Bewegungsgleichung:
&s& +
g
⋅s = 0
l
(1.16)
⇒ analoge Weg-Zeit-Funktion wie bei Federschwinger:
s (t ) = sˆ ⋅ sin(ω ⋅ t + ϕ 0 ) oder
β (t ) = βˆ ⋅ sin(ω ⋅ t + ϕ )
(1.17)
0
aber mit einer anderen Eigenfrequenz:
ω=
g
= ω0
l
(1.18)
--------------------------------------------------------------------------------------------Internetseite der LV:
http://fh-web1.informatik.fh-wiesbaden.de
/lvdetail.cfm/fb/10/lvid/1705/sprachid/1/pid/765/semester/65.html
Blatt 6
FACHHOCHSCHULE WIESBADEN
Prof. Dr. Uwe Langbein
FB 10-Physikalische Technik
Physik 2 für Maschinenbauer
"Schwingungen und Wellen"
1.2.2.3 Der Torsionsschwinger (Drehpendel)
Ansicht von oben: (Rücktreibende Schneckenfeder nicht
gezeigt)
Pendelscheibe
β
Ruhelage
Drehachse
β(t) = Auslenkungswinkel
Wesentliche Drehmomente:
M Rück = − D * ⋅ β
(1.19)
M Trägh = − J ⋅ β&&
(1.20)
D* = Winkelrichtgröße ; [D*] = Nm
(entspricht der Federkonstante beim Federschwinger)
MRück = rücktreibendes Torsions-Drehmoment; [MRück] = Nm
(entspricht der rücktreibenden Kraft beim Federschwinger)
J = Trägheitsmoment der Pendelscheibe; [J] = kgm²
(entspricht der Masse beim Federschwinger)
MRück = Trägheits-Drehmoment; [MTräg] = Nm
(entspricht der Trägheitskraft beim Federschwinger)
β&& =
d 2β
= α = Winkelbeschleunigung
dt 2
Drehmomenten-Gleichgewicht: Mrück + MTräg = 0 führt über die
Bewegungsgleichung
zur Weg-Zeit-Funktion analog zum Federschwinger:
β (t ) = βˆ ⋅ sin(ω ⋅ t + ϕ 0 )
(1.21)
aber mit einer anderen Eigenfrequenz:
ω=
D*
= ω0
J
(1.22)
--------------------------------------------------------------------------------------------Internetseite der LV:
http://fh-web1.informatik.fh-wiesbaden.de
/lvdetail.cfm/fb/10/lvid/1705/sprachid/1/pid/765/semester/65.html
Blatt 7
FACHHOCHSCHULE WIESBADEN
Prof. Dr. Uwe Langbein
FB 10-Physikalische Technik
Physik 2 für Maschinenbauer
"Schwingungen und Wellen"
1.2.3 Energiebilanz bei ungedämpften Schwingungen
A)
Federschwinger:
Kinetische Energie: Ekin =
1 2 1
mv = mω 0 2 yˆ 2 cos 2 (ω 0t + ϕ 0 )
2
2
(1.23)
(bei der Umformung wurde Gl. (1.6) verwendet.)
Maximale kinetische Energie:
1
2
EMaxkin = Eˆkin = mω0 yˆ 2
2
(1.23a)
Potentielle Energie einer gespannten Feder::
(bei der Umformung wurde Gl. (1.12) verwendet.)
Maximale potentielle Energie:
1
2
EMaxpot = Eˆ pot = mω0 yˆ 2
2
(1.24a)
Während des Schwingungsvorgangs wandeln sich beide
Energieformen ständig ineinander um. Ihre Summe bleibt
jedoch konstant = Erhaltung der Gesamtenergie. Das ist
typisch für eine ungedämpfte Schwingung.
1
2
Ekin + Epot = Eges = mω0 yˆ2 = konstant
2
B)
Mathematisches Pendel
1
1
2
2
Eges = mω0 ⋅ sˆ2 = mω0 l2βˆ 2
2
2
C)
(1.25)
(1.26)
Torsionsschwinger
1
2
Eges = J ⋅ω0 ⋅ βˆ 2
2
(1.27)
Experimente: POHLsches Rad, Federschwinger,
Fadenpendel, FOUCAULT-Pendel, Torsionspendel
--------------------------------------------------------------------------------------------Internetseite der LV:
http://fh-web1.informatik.fh-wiesbaden.de
/lvdetail.cfm/fb/10/lvid/1705/sprachid/1/pid/765/semester/65.html
Blatt 8
FACHHOCHSCHULE WIESBADEN
Prof. Dr. Uwe Langbein
FB 10-Physikalische Technik
Physik 2 für Maschinenbauer
"Schwingungen und Wellen"
Energieverhältnisse bei einer harmonischen
Schwingung
Die Summe aus potentieller und kinetischer Energie (Eges)
bleibt gleich:
ENERGIEERHALTUNG !
--------------------------------------------------------------------------------------------Internetseite der LV:
http://fh-web1.informatik.fh-wiesbaden.de
/lvdetail.cfm/fb/10/lvid/1705/sprachid/1/pid/765/semester/65.html
Blatt 9
FACHHOCHSCHULE WIESBADEN
Prof. Dr. Uwe Langbein
FB 10-Physikalische Technik
Physik 2 für Maschinenbauer
"Schwingungen und Wellen"
1.3 GEDÄMPFTE HARMONISCHE SCHWINGUNGEN
Reibung berücksichtigt
Der Einfluß der Reibung auf die Bewegung des Schwingers
hängt vom Typ der Reibungskraft (Dämpfungsmechanismus)
ab.
•
Konstante Reibungskraft (z.B. Lagerreibung)
yˆ i − yˆ i +1 = konst.
•
geschwindigkeitsabhängige Reibungskraft (z.B. Innere
Reibung bei elastischer Verformung)
yˆi
= konst.
yˆi +1
--------------------------------------------------------------------------------------------Internetseite der LV:
http://fh-web1.informatik.fh-wiesbaden.de
/lvdetail.cfm/fb/10/lvid/1705/sprachid/1/pid/765/semester/65.html
Blatt 10
FACHHOCHSCHULE WIESBADEN
Prof. Dr. Uwe Langbein
FB 10-Physikalische Technik
Physik 2 für Maschinenbauer
"Schwingungen und Wellen"
In der Vorlesung wird nur die geschwindigkeitsabhängige
Reibungskraft FReib behandelt:
F Reib = −b ⋅ v (v = y& )
(1.28)
(b = Reibungskoeffizient)
Aus dem nun erweiterten Kräftegleichgewicht:
FRück (t) + FTräg (t) + FReib(t) = 0
ergibt sich die WEG-ZEIT-FUNKTION für den gedämpften
Schwinger:
y (t ) = yˆ 0 ⋅ e −δ ⋅t ⋅ cos(ω d ⋅ t + ϕ 0 )
(1.29)
Die neuen Formelzeichen bedeuten:
b
= ABKLINGKOEFFIZIENT
2m
D
ωd =
− δ 2 = ω 20 − δ 2
m
δ =
[δ] = s-1
(1.30)
(1.31)
ωd = veränderte EIGENFREQUENZ
Td = 2•π/ωd
Td = veränderte SCHWINGUNGSDAUER
Grafische Darstellung der Weg-Zeit-Funktion
für verschiedene Abklingkoeffizienten:
δ = ω0
δ > ω0
δ < ω0
Wesentlicher Effekt: Die Schwingungsamplituden nehmen ab.
Verhältnis zweier benachbarter Amplituden:
q=
yˆ i
= eδ T d
yˆi +1
Logarithmisches Dekrement Λ: Λ = ln(q ) = δ ⋅ Td
(1.32)
(1.32a)
--------------------------------------------------------------------------------------------Internetseite der LV:
http://fh-web1.informatik.fh-wiesbaden.de
/lvdetail.cfm/fb/10/lvid/1705/sprachid/1/pid/765/semester/65.html
Blatt 11
FACHHOCHSCHULE WIESBADEN
Prof. Dr. Uwe Langbein
FB 10-Physikalische Technik
Physik 2 für Maschinenbauer
"Schwingungen und Wellen"
NEU: Bei einer gedämpften Schwingung SINKT die
Gesamtenergie EGes im Verlauf der Zeit:
EGes = 12 D ⋅ yˆ 0 ⋅ e −2δ ⋅t
2
(1.33)
Durch die Reibungskraft wird die Schwingungsenergie
allmählich in Wärmeenergie umgewandelt
Experimente: POHLsches Rad, Gedämpfter Federschwinger,
Stimmgabel
1.4 ERZWUNGENE (ERREGTE) SCHWINGUNGEN
Bisher wurden FREIE schwingende Systeme behandelt, die nach
einmaliger Auslenkung ungestört ausschwingen können.
Reibung berücksichtigt
Bei ERZWUNGENEN Schwingungen wird das System durch eine
periodisch ( mit der Kreisfrequenz ωE) einwirkende äußere Kraft
FErr zum Mitschwingen gezwungen.
D
Erreger-Kraft:
D•y
F = FˆErr sin(ω E ⋅ t )
(1.34)
ωE = Kreisfrequenz der periodischen Erreger-Kraft
F̂Err = Amplitude der Erreger-Kraft
Aus der Gleichgewichtsbedingung der 4 Kräfte: Trägheitskraft,
rücktreibende Kraft der Feder, Reibungskraft und Erreger-Kraft
läßt sich die
Weg-Zeit-Funktion einer erzwungenen Schwingung
berechnen:
y (t ) = yˆ (ω E ) ⋅ sin(ω E ⋅ t − ϕ E (ω E ))
(1.35)
Aus Gl. (1.35) erkennt man, dass der Schwinger jetzt mit der
Erreger-Kreisfrequenz ωE und nicht mehr mit seiner
Eigenfrequenz schwingt.
--------------------------------------------------------------------------------------------Internetseite der LV:
http://fh-web1.informatik.fh-wiesbaden.de
/lvdetail.cfm/fb/10/lvid/1705/sprachid/1/pid/765/semester/65.html
Blatt 12
FACHHOCHSCHULE WIESBADEN
Prof. Dr. Uwe Langbein
FB 10-Physikalische Technik
Physik 2 für Maschinenbauer
"Schwingungen und Wellen"
Die Amplitude (= maximale Auslenkung) der erzwungenen
Schwingung hängt zudem stark von der Erreger-Kreisfrequenz
ωE ab:
FˆE
yˆ (ω E )⋅ =
m
1
[(ω 0
2
− ω E ) 2 + 4δ 2ω E ]
2
2
(1.36)
Zudem stellt sich eine Phasenverschiebung zwischen ErregerKraft und der erzwungenen Schwingung ein:
⎛ 2δ ⋅ ω E ⎞
⎟
2
2 ⎟
⎝ ω0 − ωE ⎠
ϕ E (ω E ) = arctan⎜⎜
(1.37)
--------------------------------------------------------------------------------------------Internetseite der LV:
http://fh-web1.informatik.fh-wiesbaden.de
/lvdetail.cfm/fb/10/lvid/1705/sprachid/1/pid/765/semester/65.html
Blatt 13
FACHHOCHSCHULE WIESBADEN
Prof. Dr. Uwe Langbein
FB 10-Physikalische Technik
Physik 2 für Maschinenbauer
"Schwingungen und Wellen"
Wichtige Grenzfälle:
A)
Quasistatischer Grenzfall:
ωE << ω0
Aus den Gln. (1.36) und (1.37) folgt für diesen Fall:
yˆ (ω E )⋅ ≡ yˆ stat =
Fˆ E 1
Fˆ E
=
m ω02
D
(1.36a)
ϕ E (ω E ) ≈ 0 ,
d.h., der Schwinger bewegt sich, als sei er starr mit dem
Erreger gekoppelt.
B)
Resonanzfall:
ω E ≈ ω R = ω 2 0 − 2δ 2
(1.38)
ωR heißt RESONANZFREQUENZ.
Im Resonanzfall nimmt die Amplitude des Schwingers
maximale Werte an; sie schaukelt sich auf.
Bei kleinen Abklingkoeffizienten δ können die großen
Schwingungsamplituden zur Zerstörung der Schwingers führen
(Resonanzkatastrophe)! Aus Gl.(1.36) läßt sich für
ωE = ω0 berechnen:
FˆE
1
yˆ (ω R )⋅ =
m 2δ ⋅ [(ω 2 − δ 2 ]
0
C)
Hochfrequenter Grenzfall:
(1.36b)
ωE >> ω0
Bei hoher Erregerfrequenz wird die Schwingungsamplitude sehr
klein; Schwinger und erregende Kraft bewegen sich
gegenphasig.
Aus den Gln. (1.36) und (1.37) folgt für diesen Fall:
yˆ (ω E >> ω 0 )⋅ ≈ 0
ϕ E (ω E >> ω 0 ) ≈ π
.
Alle drei Fälle lassen sich auch aus der Grafik auf der vorigen
Seite studieren.
Experimente:
POHLsches Rad, Magnetisch getriebenes Federblatt,
gekoppelte Stimmgabeln, Resonanzrohr, Schaukel
10/03
--------------------------------------------------------------------------------------------Internetseite der LV:
http://fh-web1.informatik.fh-wiesbaden.de
/lvdetail.cfm/fb/10/lvid/1705/sprachid/1/pid/765/semester/65.html
Blatt 14
FACHHOCHSCHULE WIESBADEN
Prof. Dr. Uwe Langbein
FB 10-Physikalische Technik
Physik 2 für Maschinenbauer
"Schwingungen und Wellen"
Übungsaufgaben zum Kapitel
"SCHWINGUNGEN"
Ungedämpfte Schwingungen
1.1
Ein Körper führt eine ungedämpfte harmonische
Schwingung aus. Die Weg-Zeit-Funktion seiner Bewegung
lautet:
y(t ) = 1,0m ⋅ sin(π s −1 ⋅ t +
5π
)
6
a) Finden Sie für diese Schwingung:
• die Eigenfrequenz ω
• die Schwingungsdauer T
• den Nullphasenwinkel ϕ0
• die Amplitude ŷ
b)
Wie groß sind für den Körper zum Zeitpunkt t = 2,0 s
• die momentane Auslenkung y(2s)
• die momentane Geschwindigkeit v(2 s ) = y& (2 s )
• die momentane Beschleunigung a (2 s ) = v&(2 s ) ?
1.2 Die Maximalamplitude einer ungedämpften Schwingung
beträgt 10 cm, die Periodendauer 5 s. Wie groß sind
Maximalgeschwindigkeit
und
–beschleunigung
der
Schwingung?
1.3 Ein an einem Seil hängender Körper führt in 30 s
10 Perioden aus. Der Weg von einem Umkehrpunkt zum
anderen beträgt 30cm. Berechnen Sie die Auslenkung nach
1s, 2s, 5s und 5 min. Alle Zeiten ti zählen vom ersten
beobachteten Durchgang des Pendels durch seine Nullage.
1.4 In einem Spielwarengeschäft hängt, an einer Feder
befestigt, eine Holzmöve der Masse m = 400 g von der
Decke. Durch die Kraft eines Kindes von 15 N wird die
Feder 12 cm nach unten ausgelenkt und dann losgelassen.
Berechnen Sie Schwingungsdauer und maximale
Geschwindigkeit der entstehenden Schwingung.
1.5 Im schwerelosen Raum (z.B. in einer Raumstation) soll die
Masse eines Körpers bestimmt werden. Hierzu wird er mit
einer Feder (Federkonstante D = 1,2 N/cm ) verbunden und
zum Schwingen gebracht. Folgende Werte werden
gemessen: Schwingungsfrequenz f = 1.8 Hz; Schwingungsamplitude A = 22 cm.
a) Berechnen
Sie
die
Masse
des
Körpers.
Welches Gewicht hätte der Körper auf der Erde?
b) Nach welcher Zeit hat sich der Körper nach dem
Start um 11 cm von seiner Ruhelage entfernt, aus er
gestartet ist?
c) Mit welcher Geschwindigkeit v0 wurde der Körper aus
seiner Ruhelage gestartet?
--------------------------------------------------------------------------------------------Internetseite der LV:
http://fh-web1.informatik.fh-wiesbaden.de
/lvdetail.cfm/fb/10/lvid/1705/sprachid/1/pid/765/semester/65.html
Blatt 15
FACHHOCHSCHULE WIESBADEN
Prof. Dr. Uwe Langbein
FB 10-Physikalische Technik
Physik 2 für Maschinenbauer
"Schwingungen und Wellen"
1.6 Auf einer waagerecht schwingenden Platte liegt ein Block.
Die Platte schwingt harmonisch in waagerechter Richtung
mit der Frequenz 2 Hz. Die Haftreibungszahl zwischen
Block und Platte sei 0,5. Wie groß darf die Amplitude ŷ der
Plattenschwingung höchstens sein, damit der Block nicht
von der Platte rutscht?
Hinweis: Der Körper beginnt zu rutschen, wenn seine
Trägheitskraft die Reibungskraft übersteigt.
1.7 Der Fahrer eines Traktors wiegt 72 kg. Der Sitz seines
Traktors [ mSitz = 1,5 kg] ist auf einer elastischen Feder
montiert. Wenn sich der Fahrer auf seinen Sitz fallen läßt,
schwingen Fahrer und Sitz zusammen mit der Frequenz
f2 = 1,5 s-1.
a) Mit welche Frequenz [f1] würde der Sitz alleine
schwingen?
b) Um welche Strecke senkt sich der Sitz, wenn der
Fahrer Platz nimmt?
1.8 Der Kolben eines Viertaktmotors besitzt zur Zeit t0 = 0s die
Auslenkung y(t0) = 5cm, die Geschwindigkeit v(t0) = 20m/s
und die Beschleunigung a(t0) = -2000m/s². Wie groß sind
die Drehzahl und der Hub des Motors, wenn die Bewegung
des Kolbens durch eine harmonische Schwingung
beschrieben werden kann?
Gedämpfte Schwingungen
1.9 Eine gedämpfte Schwingung startet mit maximaler Amplitude und hat nach 20 s nur noch l% ihrer Anfangsamplitude.
Wie groß ist der Abklingkoeffizient der Schwingung?
1.10 Gesucht ist das logarithmische Dekrement eines mathematischen Pendels, wenn die Amplitude der Schwingungen
nach 1,2 min. auf 1/5 abgeklungen ist (Pendellänge 1,5 m).
Berechnen Sie auch die Differenz Δω zwischen den Eigenfrequenzen des ungedämpften und des gedämpften
Pendels.
1.11 Die zweite Amplitude einer gedämpften Schwingung ist
um 1,0mm kleiner als die 30,0mm große erste Amplitude.
Wie groß ist die 10. Amplitude?
--------------------------------------------------------------------------------------------Internetseite der LV:
http://fh-web1.informatik.fh-wiesbaden.de
/lvdetail.cfm/fb/10/lvid/1705/sprachid/1/pid/765/semester/65.html
Blatt 16
FACHHOCHSCHULE WIESBADEN
Prof. Dr. Uwe Langbein
FB 10-Physikalische Technik
Physik 2 für Maschinenbauer
"Schwingungen und Wellen"
Erzwungene Schwingungen
1.12 Ein Schwinger mit der Masse m = 10g, der Kreisfrequenz
ω0=15,7 s-1 und dem Abklingkoeffizienten δ=0,786 s-1 wird
durch eine Erregerschwingung mit der Kraftamplitude FE =
0,0123N
und der Kreisfrequenz ω = 12,0 s-1 zum
Schwingen angeregt.
a) Mit welcher Phase und mit welcher Amplitude folgt die
erregte Schwingung der Erregerschwingung?
b) Bei welcher Erregerkreisfrequenz ωres tritt Resonanz auf,
und wie groß ist die Resonanzamplitude?
1.13 Die Stoßstellen der Betonplatten auf einer Autobahn sind
7.5 m entfernt. Wie schnell fährt ein LKW, wenn infolge der
Stöße die Fahrerkabine in Resonanz gerät. Die Kabinenfedern werden durch die Masse des Fahrers (87 kg) um
1,25 cm zusammengedrückt. Das Gewicht der Fahrerkabine
beträgt 125 kg. Für diese Überschlagsrechnung vernachlässige man die Dämpfung der Kabinenfedern.
1.14 Eine Masse m = 300kg ist auf Federelementen gelagert,
die bei statischer Belastung um s= 4cm deformiert sind.
a) Wie groß ist die Eigenfrequenz der Anordnung?
b) Wie groß ist die Resonanzfrequenz, wenn bei der freien
gedämpften Schwingung innerhalb von 3 Schwingungen
eine Amplitudenabnahme um 95% auftritt?
c) Mit welcher Amplitude schwingt die Masse, wenn sie mit
einer Kraft von maximal 5 kN zu einer erzwungenen
Schwingung angeregt wird und die Kraft zeitlich nach
einer Sinusfunktion mit einer Erregerfrequenz von 3 Hz
variiert?
--------------------------------------------------------------------------------------------Internetseite der LV:
http://fh-web1.informatik.fh-wiesbaden.de
/lvdetail.cfm/fb/10/lvid/1705/sprachid/1/pid/765/semester/65.html
Blatt 17
FACHHOCHSCHULE WIESBADEN
Prof. Dr. Uwe Langbein
FB 10-Physikalische Technik
Physik 2 für Maschinenbauer
"Schwingungen und Wellen"
Kurzlösungen zu den Übungsaufgaben des Kapitels
"SCHWINGUNGEN"
Ungedämpfte Schwingungen
Aufgabe 1.1:
a) Eigenfrequenz ω0 = 3,14 s-1 ¸Schwingungsdauer T0 = 2s;
Nullphasenwinkel ϕ0 = 5π / 6; Amplitude ŷ = 1,0m.
b) momentane Auslenkung y(2s) = 0,5m; momentane
Geschwindigkeit v( 2 s ) = y& (2 s ) = −2,72m/s;
momentane Beschleunigung a ( 2 s ) = v&( 2 s ) = -4,935 m/s².
Aufgabe 1.2: vmax = 0,126 m/s; amax = 0,158 m/s²
Aufgabe 1.3: y(1s) = 13 cm; y(2s) = = y(5s) = -13 cm; y(300s) = 0 cm.
Aufgabe 1.4:
T = 0,36 s; vmax = v̂ = 2,12 m/s
Aufgabe 1.5: a) m = 0,938 kg; b) t1 = 46 ms
c) v0 = 2,49 m/s.
Aufgabe 1.6: ŷ =31 mm.
Aufgabe 1.7: a) f1 = 10,5 Hz; b) Δs = 0,108 m.
Aufgabe 1.8: f = 31,8 s-1, Hub = 22,4cm.
Gedämpfte Schwingungen
Aufgabe 1.9: δ = 0,230 s-1.
Aufgabe 1.10: Λ = 0,055;
Δω = 10-4 1/s
Aufgabe 1.11: yˆ10 = 22,11mm .
Erzwungene Schwingungen
Aufgabe 1.12:
a) ξ(ωE) = 0,182 rad;
yˆ (ω E ) = 11,80mm ;
b)
ωRes = 15,66 s-1;
yˆ (ω Re s ) = 49,9mm
Aufgabe 1.13: v = 77,12 km/h.
Aufgabe 1.14:
a) f0 = 2,492 Hz; b) fRes = 2,430 Hz; c) yˆ (3Hz ) = 0,116m .
--------------------------------------------------------------------------------------------Internetseite der LV:
http://fh-web1.informatik.fh-wiesbaden.de
/lvdetail.cfm/fb/10/lvid/1705/sprachid/1/pid/765/semester/65.html
Blatt 18