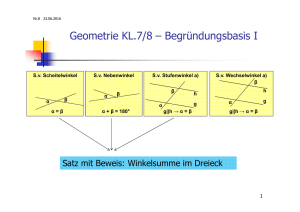
Welche Begründungsbasis ?

Nr. 15.06.2015
Welche Begründungsbasis ?
Begründungsbasis I:
•
•
•
•
S.v.
S.v.
S.v.
S.v.
Scheitelwinkel
Nebenwinkel
Stufenwinkel (dazu evtl. S.v. Wechselwinkel)
gleichschenkligen Dreieck
Satz: Winkelsumme; Satz: Thales
• S.v.d. Mittelsenkrechten
• S.v.d. Winkelhalbierenden
Satz: Umkreis;
Satz: Inkreis
1
Nr. 15.06.2015
Welche Begründungsbasis ?
Begründungsbasis I - Abschluss:
Scheitelwinkel
Nebenwinkel
Stufenwinkel (dazu evtl. S.v. Wechselwinkel)
gleichschenkligen Dreieck
Satz: Winkelsumme; Satz: Thales
• S.v.d. Mittelsenkrechten
• S.v.d. Winkelhalbierenden
Satz: Umkreis; Satz: Inkreis
•
•
•
•
S.v.
S.v.
S.v.
S.v.
• S.v.d. Mittelparallele im Dreieck
2
Nr. 15.06.2015
Mittelpararallele im Dreieck
S.v.d. Mittelparallele im Dreieck:
In jedem Dreieck ist die Verbindungsstrecke zweier
Seitenmitten parallel zur dritten Seite und halb so
lang wie diese.
C
Mb
x
A
Ma
x
B
3
Nr. 15.06.2015
Satz von Varignon (ca. 1700)
Die Verbindungstrecken der Seitenmitten eines
Vierecks bilden ein Parallelogramm.
Mc
x
D
Md
x
A
C
Mb
x
Ma
x
B
4
Nr. 15.06.2015
Kongruenz
„Definition“ (Schule): Zwei Figuren heißen
kongruent, wenn sie deckungsgleich sind.
Deckungsgleich bedeutet: Die Figuren passen ohne
Überstand aufeinander; dazu kann man sie
umdrehen, drehen, verschieben.
5
Nr. 15.06.2015
Kongruenzsatz sss
1) Wenn zwei Dreiecke in allen drei Seiten
übereinstimmen, dann sind sie kongruent
Zur Begründung sollen die Schüler alle möglichen
Dreiecke mit den Seitenlängen 6cm, 5cm, 3cm
zeichnen.
3
5
6
Ergebnis:
Alle diese Dreiecke sind
deckungsgleich.
6
Nr. 15.06.2015
Kongruenzsatz sws
2) Wenn zwei Dreiecke in zwei Seiten und dem
eingeschlossenen Winkel übereinstimmen, dann
sind sie kongruent.
s
w
s
7
Nr. 15.06.2015
Kongruenzsatz Ssw
3) Wenn zwei Dreiecke in zwei Seiten und dem
Gegenwinkel der größeren Seite übereinstimmen,
dann sind sie kongruent.
S
w
s
8
Nr. 15.06.2015
Kongruenzsatz wsw
4) Wenn zwei Dreiecke in einer Seite und den zwei
der Seite anliegenden Winkeln übereinstimmen,
dann sind sie kongruent (sws)
w
w
s
9
Nr. 15.06.2015
Kongruenzsatz sww
5) Wenn zwei Dreiecke in einer Seite und in zwei
Winkeln übereinstimmen, die nicht die anliegenden
Winkel sind?
Dann wird der dritte
Winkel berechnet oder
konstruiert.
Dann kann wsw
angewendet werden.
w
w
s
10
Nr. 15.06.2015
Der Höhensatz
Die Höhen in einem Dreieck schneiden sich in einem
Punkt.
C
hb
ha
A
hc
B
11
Nr. 15.06.2015
Der Höhensatz
Beweis: Die Höhen sind im Dreieck A*B*C* die
Mittelsenkrechten.
C
B*
Parallele zu AB
A*
Beweis (für hc):
1) hc orthogonal B*A*
(Stufenwinkel)
2) C ist die Mitte von
B*A*.
Zu 2) Die Dreiecke
ACB*, BA*C, B*BA
sind kongruent zu
ABC.
hb
ha
A
hc
B
Parallele zu AC
Parallele zu BC
B*
12
Nr. 15.06.2015
Der Höhensatz
Die Dreiecke ACB* und ABC sind kongruent nach
wsw.
C
B*
Beweis:
1) α* = α
(Wechselw. an AC)
2) γ* = γ
(Wechselw. an AC)
3) Beide Dreiecke haben
die Seite AC gemeinsam.
4) Die Dreiecke sind
kongruent.
5) Entsprechende Seiten
sind gleichlang: B*C = AB.
(Seite mit Winkeln α,γ.)
A*
α*
γ
hb
ha
γ*
α
A
hc
B*
B
13
Nr. 15.06.2015
Der Satz vom Schwerpunkt
Definition: In einem Dreieck heißt die Strecke von
einer Ecke zur Mitte der gegenüberliegenden Seite
Seitenhalbierende (oder Schwerelinie).
C
Satz:
a) Die Seitenhalbierenden
schneiden sich in einem
gemeinsamen Punkt S.
b) Es gilt:
AS=2·SMa
BS=2·SMb
CS=2·SMc
Mb
Ma
S
A
Mc
B
14
Nr. 15.06.2015
Der Satz vom Schwerpunkt
Beweis:
Zeichne Mitten M1 bzw. M2
von AS bzw. BS.
C
1) MbMa=M1M2 und parallel
2) u = u*; v = v*
Mb
3) M1M2S ~ SMaMb
Ma
S
M1
4) M1S=SMa; M2S=SMb
5) AS=2·SMa; BS=2·SMb
u*
v*
u
v M2
A
Die dritte Seitenhalbierende CMc muss durch S gehen, da CMc
die Seitenhalbierende AMa im Verhältnis 2:1 teilt.
B
15
Nr. 15.06.2015
Der Satz von Napoleon
Errichtet man über jeder
Seite eines Parallelogramms
ein Quadrat, so bilden auch
die Quadratmitten ein
Quadrat.
Beweis: Zu zeigen
1) PQ = QR und
2) Bei Q bilden PQ und QR
einen rechten Winkel.
Tipp:
Die Dreiecke PDQ und RCQ
sind kongruent nach sws.
16