Kapitel 5 Flüsse in Netzwerken Netzwerke Netzwerke

Netzwerke
• Stromnetz
• Telefonnetz
• Warenfluss zwischen Herstellern und
Konsumenten
• Verkehr (Straßen, Züge, Flugzeuge, ...)
Kapitel 5
ƒ Oft wollen wir Güter von einem
Punkt zu einem anderen schicken
ƒ Ziel
Flüsse in Netzwerken
• So viel/effizient/billig wie möglich
Maximale Flüsse (diese Vorlesungseinheit)
Technische Universität Wien
Institut für Computergraphik und Algorithmen
Technische Universität Wien
1
2
Institut für Computergraphik und Algorithmen
Netzwerke
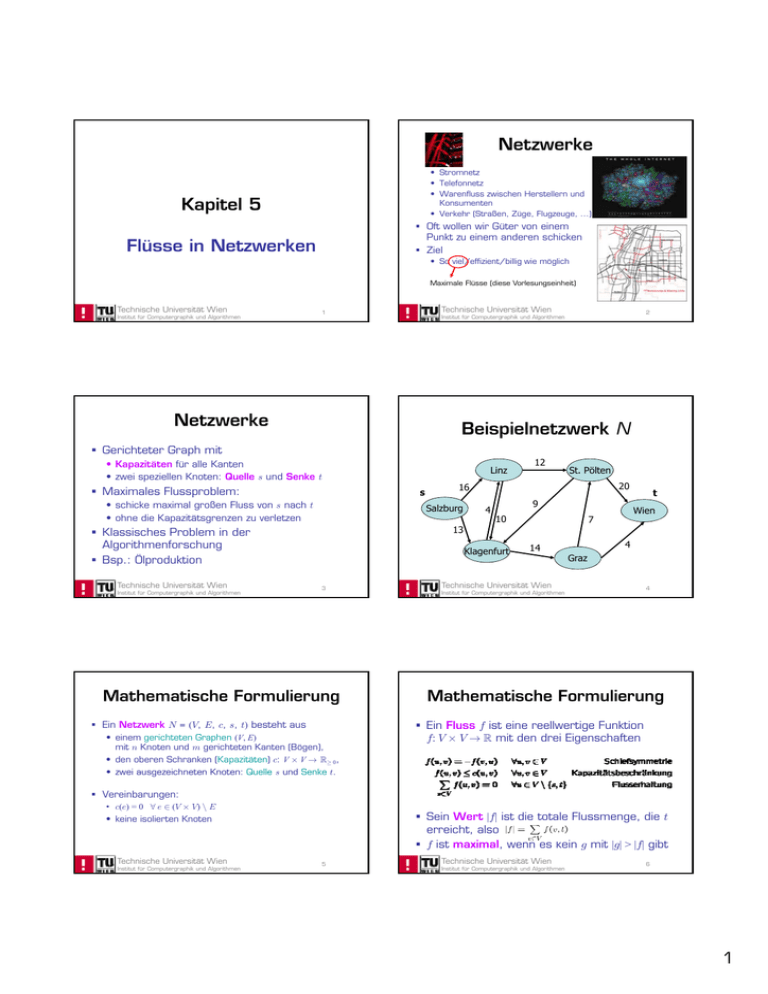
Beispielnetzwerk N
ƒ Gerichteter Graph mit
• Kapazitäten für alle Kanten
• zwei speziellen Knoten: Quelle s und Senke t
ƒ Maximales Flussproblem:
p
s
• schicke maximal großen Fluss von s nach t
• ohne die Kapazitätsgrenzen zu verletzen
Institut für Computergraphik und Algorithmen
12
St. Pölten
20
16
Salzburg
4
9
10
Klagenfurt
3
Mathematische Formulierung
ƒ Ein Netzwerk N = (V, E, c, s, t) besteht aus
• einem gerichteten Graphen (V, E)
mit n Knoten und m gerichteten Kanten (Bögen),
14
t
Wien
7
13
ƒ Klassisches Problem in der
Algorithmenforschung
ƒ Bsp.: Ölproduktion
Technische Universität Wien
Linz
4
Graz
Technische Universität Wien
Institut für Computergraphik und Algorithmen
4
Mathematische Formulierung
ƒ Ein Fluss f ist eine reellwertige Funktion
f: V × V → R mit den drei Eigenschaften
• den oberen Schranken (Kapazitäten) c: V × V → R≥ 0,
• zwei ausgezeichneten Knoten: Quelle s und Senke t.
t
ƒ Vereinbarungen:
• c(e) = 0 ∀ e ∈ (V × V) \ E
• keine isolierten Knoten
Technische Universität Wien
Institut für Computergraphik und Algorithmen
ƒ Sein Wert |f| ist die totale Flussmenge, die t
erreicht, also
ƒ f ist maximal, wenn es kein g mit |g| > |f| gibt
5
Technische Universität Wien
Institut für Computergraphik und Algorithmen
6
1
Restgraph
Bsp.: Ein Fluss f in N
Linz
12/12
ƒ Sei f ein Fluss in N. Die Restkapazität einer
Kante e bezüglich f ist
St. Pölten
15/20
11/16
Salzburg
1/4
4/9
10
Wien
7/7
4/4
11/14
Technische Universität Wien
7
Institut für Computergraphik und Algorithmen
Residualgraph für f
12/12
Linz
St. Pölten
15/20
11/16
Salzburg
1/4
4/9
10
Klagenfurt
Linz
11
Salzburg
5
3 11
12
5
8
7/7
Klagenfurt
11/14
4/4
St. Pölten
5
Wien
7
11
Salzburg
3 11
Institut für Computergraphik und Algorithmen
10
Klagenfurt
12
5
Wien
7/7
4/4
11/14
Graz
St. Pölten
5
15
4
Wien
7
3
11
Graz
Technische Universität Wien
10
Institut für Computergraphik und Algorithmen
Flusserhöhung
Beispiel
ƒ Push um x auf einer Kante e = (u,v):
Push um x = 4 auf den roten Kanten
• erhöhe f(u,v) um x
• erniedrige f(v,u) um x
Linz
Sei P s-t-Pfad in Gf
Sei x minimale Restkapazität auf P
push(e,x) für alle e auf P
Neuer Fluss f ’ mit Wert |f ’| = |f| + x
12/12
St. Pölten
15/20
19
11/16
Salzburg
1/4
04/9
10
7/7
128/13
Klagenfurt
Institut für Computergraphik und Algorithmen
4/9
4
Klagenfurt
9
15/20
1/4
8/13
8
5
Graz
Technische Universität Wien
Technische Universität Wien
Salzburg
Linz
5
St. Pölten
11/16
Graz
4
3
11
ƒ
ƒ
ƒ
ƒ
Wien
12/12
Linz
Beispiel:
augmentierender
Pfad
15
4
8
Institut für Computergraphik und Algorithmen
8/13
5
„um wieviel kann
ich f auf e
erhöhen, ohne die
Kapazität c(e) zu
überschreiten?“
ƒ Ein s-t-Pfad in Gf heißt
augmentierender Pfad
Graz
Technische Universität Wien
e ist Restkante
e ist saturiert
ƒ Der Graph Gf = (V, Ef) ist
der Graph der Restkanten
(Restgraph, Residualgraph)
8/13
Klagenfurt
• rf (e) > 0
• rf ((e)) = 0
11
11/14
Technische Universität Wien
Institut für Computergraphik und Algorithmen
Wien
4/4
Graz
12
2
Korrektheit
ƒ
Schnitt
Ist f ’ ein gültiger Fluss?
ƒ Ein Schnitt ist eine Knotenmenge
• Schiefsymmetrie?
Durch Definition der push-Operation
• Kapazitätsbeschränkung?
Durch Definition des Restgraphen
• Flusserhaltung
Für innere Knoten wird sowohl der eingehende
als auch der ausgehende Fluss um x erhöht,
die Bilanz bleibt gleich (Null).
ƒ Die Kapazität eines Schnittes S in N ist
Technische Universität Wien
13
Institut für Computergraphik und Algorithmen
Lemma
Kapazitätsbeschränkung
Flusserhaltung
Gilt
14
Institut für Computergraphik und Algorithmen
Max-Flow-Min-Cut-Theorem
Kein Fluss f in N kann einen Wert haben,
der die Kapazität eines beliebigen Schnittes S
übersteigt.
ƒ Beweis:
Technische Universität Wien
Sei f ein Fluss. Die folgenden Bedingungen
sind äquivalent:
(1) Es gibt einen Schnitt S, den f saturiert
(2) Fluss f ist maximal
(3) Es gibt keinen augmentierenden Pfad
f im
Restgraphen
[Ford/Fulkerson 1956,
Elias/Feinstein/Shannon 1956]
ƒ Beweis: (Ringschluss)
Schiefsymmetrie
(1) → (2): Für jeden Fluss g gilt
, dann saturiert f den Schnitt S.
(2) → (3): Wenn es einen augmentierenden Pfad P gäbe, könnten wir
entlang P augmentieren,
Technische Universität Wien
Institut für Computergraphik und Algorithmen
15
Max-Flow-Min-Cut-Theorem
Sei f ein Fluss. Die folgenden Bedingungen sind äquivalent:
(1) Es gibt einen Schnitt S, den f saturiert
(2) Fluss f ist maximal
(3) Es gibt keinen augmentierenden Pfad im Restgraphen
1
Technische Universität Wien
Institut für Computergraphik und Algorithmen
16
Max-Flow-Min-Cut-Theorem
ƒ Warum “Max-Flow-Min-Cut”?
• Wenn f maximal ist, muss S minimal sein.
Gäbe es kleineren Schnitt S´, wäre
ƒ Beweis: (Ringschluss)
(3) → (1): Sei S die Menge aller Knoten, die in Gf von
s aus erreicht werden können.
Klar: s ∈ S und t ∉ S, also ist S Schnitt.
Nach Def. von S gilt für alle e = (u, v) mit u ∈ S und
v ∉ S, dass f(e) = c(e).
Damit ist S von f saturierter Schnitt.
Technische Universität Wien
Institut für Computergraphik und Algorithmen
17
ƒ Die Angabe eines saturierten Schnittes ist
ein Beweis für die Maximalität eines Flusses
(Dualitätstheorie).
Technische Universität Wien
Institut für Computergraphik und Algorithmen
18
3
Die Ford-Fulkerson-Methode
Maximaler Fluss
Beweis: Wert gleich minimalem Schnitt
Linz
s
12
St. Pölten
19/20
10/16
Salzburg
4
9
2/10
Klagenfurt
Wien
7
13
11/14
t
Das MCMF-Theorem sagt noch nicht, dass
jedes Netzwerk einen maximalen Fluss zulässt,
legt aber einen konstruktiven Beweis nahe
(Schritt (3) ⇒ (2)).
(2))
Der entsprechende Algorithmus heißt
Ford-Fulkerson-Methode:
Beginne mit dem Nullfluss (ist Fluss!) und
augmentiere, solange augmentierende Pfade im
Residualgraphen existieren.
4
Graz
Technische Universität Wien
19
Institut für Computergraphik und Algorithmen
Die Ford-Fulkerson-Methode
f0 := Nullfluss; i := 0;
while (∃ s-t-Pfad P in Gfi) do {
x = min.
min Restkapazität auf P;
fi+1 := fi “+” x;
i = i + 1;
}
Technische Universität Wien
Residualgraph für f0
12
16
Salzburg
4 10
9
Salzburg
4 10
14
Technische Universität Wien
Institut für Computergraphik und Algorithmen
Wien
7
14
Graz
Technische Universität Wien
22
Institut für Computergraphik und Algorithmen
Fluss f1
Linz
4/12
St. Pölten
20
4/16
Wien
Salzburg
4
4/9
10
7
13
4
Klagenfurt
20
4
Klagenfurt
20
13
9
St. Pölten
13
St. Pölten
7
12
16
Residualgraph für f0
Linz
20
Institut für Computergraphik und Algorithmen
Linz
21
Institut für Computergraphik und Algorithmen
Technische Universität Wien
Klagenfurt
Graz
23
4/14
Technische Universität Wien
Institut für Computergraphik und Algorithmen
Wien
4/4
Graz
24
4
Residualgraph für f1
8
Linz
12
Salzburg
4
4 10
4
5
4
Residualgraph für f1
St. Pölten
20
12
Wien
7
13
Klagenfurt
Klagenfurt
Fluss f2
7/10
13
Wien
5
Salzburg
Graz
27
Institut für Computergraphik und Algorithmen
11
11 3
5
Salzburg
11
11 3
4
Klagenfurt
4
3
11
Technische Universität Wien
Institut für Computergraphik und Algorithmen
5
4
Wien
7
3
Graz
28
Institut für Computergraphik und Algorithmen
Linz
12/12
St. Pölten
15/20
11/16
Wien
Salzburg
1/4
4/9
10
7/7
8/13
4
Klagenfurt
13
Fluss f3
13
7
13
St. Pölten
7
11
Technische Universität Wien
St. Pölten
7
5
4
4
Residualgraph für f2
8
26
13
4/4
Technische Universität Wien
Linz
Graz
8
Linz
7/7
11/14
10
Institut für Computergraphik und Algorithmen
St. Pölten
4/9
Klagenfurt
Wien
7
Technische Universität Wien
7/20
4
4
20
Residualgraph für f2
11/16
Salzburg
5
4
25
Institut für Computergraphik und Algorithmen
4/12
4 10
St. Pölten
4
Graz
4
Technische Universität Wien
Linz
Salzburg
4
4
13
4
10
8
Linz
Klagenfurt
Graz
29
11/14
Technische Universität Wien
Institut für Computergraphik und Algorithmen
Wien
4/4
Graz
30
5
Residualgraph für f3
Linz
5
3 11
5
4
8
5
St. Pölten
15
11
Salzburg
12
Fluss f4
5
3
11
Salzburg
1
3 11
9
Klagenfurt
32
Korrektheit: (ohne Beweis)
Algorithmus terminiert mit maximalem Fluss f,
wenn Kapazitäten ganzzahlig.
Es folgt,
folgt dass dann auch f ganzzahlig ist (was
nicht heißt, dass es keinen nicht-ganzzahligen
Fluss g mit |g| = |f| gibt).
1
Wien
7
12
Graz
Ford-Fulkerson
St. Pölten
19
4/4
11/14
Institut für Computergraphik und Algorithmen
Residualgraph für f4
5
Wien
7/7
Technische Universität Wien
31
Institut für Computergraphik und Algorithmen
12
0/9
10
Klagenfurt
Technische Universität Wien
Linz
1/4
12/13
Graz
11
19/20
Salzburg
Wien
7
St. Pölten
11/16
4
Klagenfurt
12/12
Linz
4
3
11
Technische Universität Wien
Graz
Institut für Computergraphik und Algorithmen
Technische Universität Wien
33
Ford-Fulkerson
Ford-Fulkerson: worst case
Analyse:
Laufzeit hängt davon ab, wie man die
augmentierenden Pfade wählt. Bei Wahl eines
beliebigen Pfades ergibt sich eine Laufzeit von
O(|E|·|f|) wobei f der maximale Fluss ist,
O(|E|·|f|),
ist
denn die Schleife benötigt Zeit O(|E|)
f0
a
0/106
s
und wird höchstens |f| Mal ausgeführt
35
a
0/106
106
106
t
s
0/106
0/106
(ein augmentierter Fluss muss mindestens um 1 größer
sein).
Institut für Computergraphik und Algorithmen
Gf 0
0/1
(finde Pfad mit DFS oder BFS)
Technische Universität Wien
34
Institut für Computergraphik und Algorithmen
b
Technische Universität Wien
Institut für Computergraphik und Algorithmen
t
1
106
106
b
36
6
Ford-Fulkerson: worst case
f1
a
1/106
s
Ford-Fulkerson: worst case
Gf 1
f2
a
a
0/106
t
1/1
s
1
t
1
106-1
1/106
0/106
1/106
106
106-1
106
b
1
b
s
Gf 2
a
1/106
1
106-1
t
0/1
s
1/106
1/106
106-1
1
106-1
1
1
106-1
b
t
1
b
|f2| = 2 ... |f| = 2 · 106
|f1| = 1
Technische Universität Wien
Technische Universität Wien
37
Institut für Computergraphik und Algorithmen
38
Institut für Computergraphik und Algorithmen
Verbesserung
Preflow-Push-Algorithmus
ƒ Kluge Auswahl der augmentierenden
Pfade
ƒ Z.B.: Wähle immer Pfad mit möglichst
wenigen
i
K
Kanten
t
ƒ Goldberg/Tarjan 1988. Laufzeit: O(n2m)
ƒ Ein Präfluss f ist eine reellwertige Funktion
f: V × V → R mit den drei Eigenschaften
¾Edmonds-Karp-Algorithmus
¾Laufzeit: O(nm2)
Überschuss an
Knoten v
Technische Universität Wien
Technische Universität Wien
39
Institut für Computergraphik und Algorithmen
Preflows in N
Preflows in N
Linz
12
+16
St. Pölten
s
Salzburg
Linz
20
16
4
9
10
Klagenfurt
14
Technische Universität Wien
Institut für Computergraphik und Algorithmen
12
St. Pölten
20
16
t
Wien
7
13
40
Institut für Computergraphik und Algorithmen
s
Salzburg
4
9
10
Klagenfurt
Graz
41
Wien
7
13
4
14
Technische +13
Universität Wien
Institut für Computergraphik und Algorithmen
t
4
Graz
42
7
Preflows in N
Linz
12
Preflows in N
+12
St. Pölten
20
16
s
Salzburg
Linz
4
9
4/10
13
Klagenfurt
14
Technische +17
Universität Wien
s
Salzburg
4
s
Linz
9
Klagenfurt
14
+3
Technische Universität
Wien
s
Salzburg
Salzburg
+14
St. Pölten
Linz
14
+3
Technische Universität
Wien
Institut für Computergraphik und Algorithmen
+10
12
46
St. Pölten
19/20
16
t
Wien
7
13
4
Graz
Institut für Computergraphik und Algorithmen
+7
4/10
Wien
7
14
t
Preflows in N
9
Klagenfurt
4/10
+3
Technische Universität
Wien
45
12/20
4
9
Klagenfurt
Graz
16
s
St. Pölten
12/20
4
Preflows in N
Linz
12
13
4
Institut für Computergraphik und Algorithmen
12
44
16
t
Wien
7
13
4
Graz
Institut für Computergraphik und Algorithmen
St. Pölten
4/10
Wien
7
14
t
Preflows in N
12/20
4
4/10
Technische +17
Universität Wien
43
16
Salzburg
9
Klagenfurt
Graz
Preflows in N
12
12/20
13
4
Institut für Computergraphik und Algorithmen
Linz
St. Pölten
16
t
Wien
7
12
s
Salzburg
4
9
4/10
Klagenfurt
Graz
+3
47
Wien
7
13
4
14
+3
Technische Universität
Wien
Institut für Computergraphik und Algorithmen
t
4
Graz
+3
48
8
Preflows in N
Linz
12
+6
St. Pölten
Salzburg
Linz
19/20
16
s
Preflows in N
4
9
4/10
13
Klagenfurt
11/14
+6
Technische Universität
Wien
t
s
s
Institut für Computergraphik und Algorithmen
9
Klagenfurt
11/14
50
• innere Knoten haben Vorratsbecken
• schicke
hi k Fluss
Fl
von s nach
h t und
d leere
l
alle
ll B
Becken
k
• jeder Knoten hat Höhe
t
-
Wien
7
13
4
Graz
ƒ Wie schicken wir Flüsse planvoll durch das
Netz?
ƒ Intuition
St. Pölten
2/10
Wien
7
11/14
t
Preflow-Push-Algorithmus
19/20
4
2/10
Technische Universität Wien
49
= maximaler Fluss. Beweis:
Salzburg
4
9
Klagenfurt
Graz
10/16
19/20
13
Preflows in N
12
Salzburg
4
Institut für Computergraphik und Algorithmen
Linz
St. Pölten
16
Wien
7
12
4
Am Anfang: d(s) = n, d(t) = 0, d(v) = 0 ∀ v ∈ V \ {s, t}
Fluss fließt nur nach unten
Wenn das nicht mehr geht → hebe Becken an
Kann nicht alles nach t fließen, wird es zurück zur Quelle
geschickt
Graz
Technische Universität Wien
Technische Universität Wien
51
Institut für Computergraphik und Algorithmen
Institut für Computergraphik und Algorithmen
Preflow-Push-Algorithmus
52
Preflow-Push-Algorithmus
ƒ Modelliere Höhe über Beschriftung d: V → N0
ƒ Beschriftung legal ⇔
d(s) = n, d(t) = 0 und d(v) ≥ d(u) – 1 für alle
Restkanten (u,v)
ƒ D.h. Restkanten dürfen abfallen, aber nicht zu
steil
u
>1
1
u
v 9
v 9
v 9
u
u
v
ƒ Restkante wählbar ⇔ d(v) = d(u) – 1
ƒ Knoten u aktiv ⇔ u ∈ V \ {s, t} und ef(u) > 0
saturierende und
nicht-saturierende
nicht
saturierende
Pushes
1
wählbar
Technische Universität Wien
Institut für Computergraphik und Algorithmen
53
Technische Universität Wien
Institut für Computergraphik und Algorithmen
54
9
Preflow-Push-Algorithmus
d(s) = n; for all v ∈ V \ {s}: d(v) = 0;
for all (u, v) ∈ E: f(u,v) = 0;
Initialifor all (s, v) ∈ E {
sierung
f(s,v)
f(
, ) = c(s,v);
( , )
f(v, s) = -f(s, v);
}
while (∃ aktiver Knoten u) {
if (∃ (u, v) wählbar) then push (u, v);
else lift (u);
}
Technische Universität Wien
Institut für Computergraphik und Algorithmen
55
Preflow-Push-Algorithmus
Lemma: Die Beschriftung d ist stets legal
und f immer ein Präfluss.
ƒ Beweis:
• Nach Initialisierung
g9
• Danach nur Operationen
- Lift (u): Präfluss, da Fluss sich nicht ändert
Legalität bleibt erhalten, da keine Kante wählbar
- Push (u,v): Präfluss, da neu entstehende Überschüsse ≥ 0 sind
Legalität: (u,v) fällt hinaus → push saturierend → 9
(v,u) kann hinzukommen, steigt aber an → 9
Technische Universität Wien
Institut für Computergraphik und Algorithmen
57
Preflow-Push-Algorithmus
Lemma: Wenn der Algorithmus terminiert,
ist f ein maximaler Fluss in N.
• Alg. terminiert → es existieren keine aktiven
Knoten
• → f ist Fluss
• f ist maximal wegen der letzten beiden Lemmata
und des Max-Flow-Min-Cut-Theorems
ƒ partielle Korrektheit! Jetzt zur Laufzeit...
Institut für Computergraphik und Algorithmen
ƒ Nach der Initialisierung verlaufen Restkanten
nur auf Höhe 0
ƒ Nicht offensichtlich, dass Algorithmus
terminiert
ƒ Wir zeigen
• Partielle Korrektheit
(wenn Alg. terminiert, ist Ergebnis korrekt)
(3 Lemmata)
• Laufzeitbeweis
(5 Lemmata)
Technische Universität Wien
Institut für Computergraphik und Algorithmen
56
Preflow-Push-Algorithmus
Lemma: Sei f ein Präfluss mit legaler Beschriftung d. Dann gibt es keinen augmentierenden Pfad im Restgraphen.
ƒ Beweis:
Be eis
• Sei P augmentierender Pfad von s nach t.
• P hat ≤ n – 1 Kanten.
• Da d(s) = n und d(t) = 0 und keine Kante steil
abfallen darf (d ist legal) hat P ≥ n Kanten
• Widerspruch 1
Technische Universität Wien
Institut für Computergraphik und Algorithmen
58
Preflow-Push-Algorithmus
Lemma: Sei f Präfluss und u aktiv. Dann
existiert ein u-s-Pfad im Restgraphen.
ƒ Beweis:
ƒ Beweis:
Technische Universität Wien
Preflow-Push-Algorithmus
59
• Sei T Menge der von u aus erreichbaren Knoten in
Gf. Dann gilt
• Warum ≤ 0? Weil kein f(w,v) > 0 sein kann, sonst
wäre (v,w) Restkante und w ∈ T, 1
• Da u ∈ T und ef(u) > 0, muss v mit ef(v) < 0 in der
Summe enthalten sein → v = s → s ∈ T
Technische Universität Wien
Institut für Computergraphik und Algorithmen
60
10
Preflow-Push-Algorithmus
Preflow-Push-Algorithmus
Lemma: Für jeden Knoten u ∈ V gilt stets
d(u) ≤ 2n - 1.
Lemma: Es gibt höchstens 2n2 lift-Operationen.
ƒ Beweis:
•
•
•
•
•
• Folgt direkt aus dem letzten Lemma.
• n Knoten,, d(n)
( ) ≤ 2n – 1,, d wird nur erhöht
O.B.d.A.:
O
B d A : u aktiv
Es gibt u-s-Pfad P in Gf
P hat ≤ n Kanten und d(s) = n
Keine steilen Kanten (d legal)
→ u höchstens auf Höhe n + n – 1 = 2n - 1
Technische Universität Wien
Institut für Computergraphik und Algorithmen
61
Preflow-Push-Algorithmus
Lemma: Es gibt höchstens nm saturierende Pushes.
ƒ Beweis:
• Zwischen 2 saturierenden Pushes über (u,v) muss
ein Push über (v,u) erfolgen.
• Dazu muss sowohl d(u) als auch d(v) um 2
ansteigen
• Da d(u) ≤ 2n-1, kann das höchstens (n-1)-mal
passieren → ≤ n saturierende Pushes über eine
Kante
• → insgesamt ≤ nm saturierende Pushes
Technische Universität Wien
Institut für Computergraphik und Algorithmen
ƒ Beweis:
63
Preflow-Push-Algorithmus
Lemma: Es gibt höchstens 4n2m nichtsaturierende Pushes.
• Bei einem saturierenden Push über (u,v) kann
höchstens v zu A hinzukommen, also
Technische Universität Wien
Institut für Computergraphik und Algorithmen
62
Preflow-Push-Algorithmus
Lemma: Es gibt höchstens 4n2m nichtsaturierende Pushes.
ƒ Beweis:
• Sei A die zeitlich variierende Menge aktiver Knoten
• Betrachte
(am Anfang 0, nie negativ)
• Nicht-saturierender Push über (u,v) entfernt u aus
A und fügt eventuell v hinzu. Sei Φ‘ das neue
Potenzial. Es gilt
Technische Universität Wien
Institut für Computergraphik und Algorithmen
64
Preflow-Push-Algorithmus
Satz: Der generische Preflow-Push-Algorithmus
terminiert nach O(n2m) Pushes und Lifts mit
einem maximalen Fluss.
ƒ Beweis:
• → insgesamt (letztes Lemma) maximale Erhöhung
von Φ um 2n2m durch saturierende Pushes
• Alle Lifts erhöhen Φ um maximal 2n2
• Nur nicht-saturierende Pushes erniedrigen Φ →
es gibt höchstens 2n2m+2n2 davon
Technische Universität Wien
Institut für Computergraphik und Algorithmen
65
• Die letzten acht Lemmata.
Technische Universität Wien
Institut für Computergraphik und Algorithmen
66
11