Die nicht-relativistische Quantenmechanik

Kapitel 4
Die nicht-relativistische
Quantenmechanik
4.1 Die Schrödinger-Gleichung
4.1.1 Die Wellenfunktion
1928 hat G.P. Thompson beobachtet, dass sich ein Elektron wie eine
Welle verhalten kann: Elektronbeugung.
In der Quantenmechanik wird ein Teilchen (z.B. das Elektron) mit
Hilfe einer Wellenfunktion ψ beschrieben:
ψ ≡ komplexe Wellenfunktion
Diese Funktion stellt den Zustand des Teilchens dar und beschreibt
die Wellennatur des Teilchens (Interferenz, Beugungseffekte,
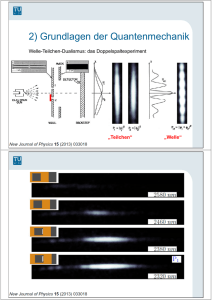
usw...). Die Wellennatur beobachtet man z.B. in Doppelspaltexperimenten.
Teilchenphysik
51
Die nicht-relativistische Quantenmechanik
Die übliche Interpretation der Wellenfunktion ist die folgende:
r 2 r
ψ ( x, t) d 3 x ≡ Wahrscheinlichkeit, das Teilchen zur Zeit t
r
im Volumenelement d 3 x zu finden.
Die Normierung wird als
r 2 3r
*
3r
∫ ψ ( x, t) d x = ∫ (ψ ψ )d x ≡ 1
V
V
ausgedrückt.
Die Wellenfunktion beschreibt den Zustand eines Teilchens. Die
Wahrscheinlichkeitsdichte wird definiert als
r
r
r
r 2
ρ( x, t) ≡ ψ * ( x, t)ψ ( x, t) = ψ ( x, t)
4.1.2 Die Operatoren
Die Wellenfunktion ist nicht beobachtbar, sondern entspricht der ganzen Information, die man über das Teilchen hat.
Die beobachtbaren Grössen werden durch hermitische Operatoren
dargestellt, die auf die Wellenfunktion wirken:
r
r
r
Impuls - Operator: p → −ih∇ = −i∇
∂
∂
Energie - Operator: E → +ih = +i
∂t
∂t
wobei wir in den zweiten Termen die natürlichen Einheiten (Siehe
Kap. 3.2) benutzt haben.
52
Teilchenphysik II&III, WS 01/02-SS02, Prof. A. Rubbia
Die Schr dinger-Gleichung
4.1.3 Die Schrödinger-Gleichung
Die Schrödinger-Gleichung wird mit Hilfe der klassischen Beziehung
zwischen Energie und Impuls “hergeleitet”. Die gesamte Energie
eines klassischen Teilchen ist gleich
E = T +V
wobei T die kinetische und V die potentielle Energie des Teilchens ist.
Es gilt,
T=
p2
2m
wobei m = Masse des Teilchens
Der Operator der gesamten Energie (der Hamilton-Operator) ist
deshalb gleich
H = T +V =
p2
+V = E
2m
Es folgt,
 p2
 r
r
r
Hψ ( x, t) = 
+ V ψ ( x, t) = Eψ ( x, t)
 2m

oder
r  r
r
∂
 1 r2
∇ + V ( x, t)ψ ( x, t) = i ψ ( x, t)
−
 2m

∂t
Diese Gleichung wurde 1926 von Schrödinger hergeleitet. Sie entspricht der Bewegungsgleichung (Wellengleichung) eines einzigen
Teilchens der Masse m in einem externen Potential V.
Teilchenphysik
53
Die nicht-relativistische Quantenmechanik
4.1.4 Die Kontinuitätsgleichung
Wir betrachten die zeitliche Änderung der Wahrscheinlichkeitsdichte
r
r
∂
∂ r
ρ( x, t) ≡ (ψ * ( x, t)ψ ( x, t))
∂t
∂t
∂ 
∂ 
=  ψ * ψ + ψ *  ψ 
 ∂t 
 ∂t 
Aus der Schrödinger-Gleichung folgt
∂
∂ *  1 r2
 1 r2


∇ + V ψ und
∇ + V ψ *
ψ = − i −
ψ = i −
 2m

 2m

∂t
∂t
Durch Einsetzen erhalten wir
∂
  1 r2
 
 1 r2

∇ + V  ψ *  ψ − ψ *i  −
ρ =  i −
∇ + V ψ
 
 2m

  2m
∂t
r
−i r 2 *
=
∇ ψ ψ − ∇ 2ψ ψ *
2m
((
) ( ) )
Das Gausssche Theorem sagt voraus, dass
r r 3r
r r
∂
3r
=
−
⋅
=
−
∇
d
x
j
dA
ρ
∫
∫V ⋅ jd x
∂t ∫V
A =∂V
wobei A die Fläche ist, die das Volumen V umschliesst, und j ist der
Wahrscheinlichkeitsstromvektor.
Wir können deshalb einen Stromdichtevektor (eine Vektorgrösse)
definieren, die die Gleichung der Kontinuität erfüllt:
r
r r
i r *
∇ψ ψ − ∇ψ ψ *
j ( x , t) ≡
2m
(( ) ( ) )
54
Teilchenphysik II&III, WS 01/02-SS02, Prof. A. Rubbia
Die Schr dinger-Gleichung
Diese Grösse beschreibt, wie die Wahrscheinlichkeitdichte ρ
“fliesst”.
Wir bemerken, dass wie erwartet, gilt
r r
r r
i r r *
∇⋅ j =
∇ ∇ψ ψ − ∇ ∇ψ ψ *
2m
r r
r r
r
i r2 *
=
∇ ψ ψ + ∇ψ *∇ψ − ∇ψ∇ψ * − ∇ 2ψ ψ *
2m
r
i r2 *
∂
=
∇ ψ ψ − ∇ 2ψ ψ * = − ρ
2m
∂t
(( ) ( ) )
(( )
(( ) ( ) )
( ) )
Freies Teilchen: Wir betrachten ein freies Teilchen.
r r
r
r
∂
1 r2
∇ ψ ⇒ ψ ( x, t) = Ne − i( Et − p ⋅x )
V ( x , t) ≡ 0 ⇒ i ψ = −
∂t
2m
Die Wellenfunktion ist eine ebene Welle. Es folgt daraus,
ρ = ψ *ψ = N
2
Einheit: 1 / L3
und
r
r r
i r *
j ( x , t) ≡
∇ψ ψ − ∇ψ ψ *
2m
r
r
i
=
(−ip)ψ *ψ − (ip)ψψ * )
(
2m
r
r
r
i
2
2 p
=
(−ip)2 N = N = N 2 v
m
2m
(( ) ( ) )
[
]
[
]
Einheit: 1 / L3 [ L / Z ] = 1 / ( ZL2 )
Teilchenphysik
55
Die nicht-relativistische Quantenmechanik
4.2 Drehimpuls und Spin
Wir werden Spin-Effekte in den Wirkungsquerschnitten von verschiedenen Prozessen betrachten. Deshalb folgt eine kurze Wiederholung
der Eigenschaften dieser Operatoren.
4.2.1 Drehimpuls-Operator
Der Drehimpuls-Operator ist gleich
r r r
r r
L ≡ r × p = −ir × ∇
Mit der Kommutationsregel
[ x, p ] = i, [ y, p ] = i,
x
y
und
[z, p ] = i
z
kann man beweisen, dass die Kommutationsregel des Drehimpulses
gleich
r
Li , L j = iε ijk Lk wobei L = ( L1, L2 , L3 )
[
]
ist. Diese Gleichung beschreibt die Lie-Algebra des DrehimpulsOperators. Der total antisymmetrische Levi-Civita Tensor εijk ist
definiert als
+1 gerade Zahl von Permutationen von 1, 2, 3

ε ijk ≡ −1 ungerade Zahl von Permutationen von 1, 2, 3
0 andernfalls

d.h., z.B.
ε123 = ε 312 = ε 231 = 1
56
und
ε 321 = ε132 = ε 213 = −1
Teilchenphysik II&III, WS 01/02-SS02, Prof. A. Rubbia
Drehimpuls und Spin
4.2.2 Spin-Operator
Es gibt kein klassisches Analog zum Spin. Er entspricht einem internen Freiheitsgrad eines Teilchens.
z.B. für Spin 1/2: zwei mögliche Zustände
↑ = s, s3 =
1 
 0
1 1
1 1
, =   und ↓ = , − =  
2 2
2 2
 0
1 
Die “spin-up” und “spin-down” Zustände sind die Eigenzustände des
Operators
1 1 0 
S3 = 

2  0 −1
Die drei Komponenten können mit Hilfe der Pauli-Matrizen σ definiert werden
r
1r
S = ( S1, S2 , S3 ) = σ
2
wobei
 0 1
σ1 = 
,
 1 0
 0 −i
σ2 = 
,
i 0
1 0 
σ3 = 

 0 −1
Die Eigenschaften dieser Matrizen sind die folgenden:
σ2 =1
σ + = σ ( Hermitisch)
[σ ,σ ] = 2iε
i
Teilchenphysik
j
σk
ijk
Lie − Algebra
57
Die nicht-relativistische Quantenmechanik
d.h. die Kommutationsregeln sind dieselben wie die des Drehimpulsoperators.
Die Pauli-Matrizen werden wir weiter brauchen, wenn wir die DiracGleichung diskutieren werden (Siehe Kap. 6).
4.3 Störungstheorie
Wir beginnen mit einer ersten wichtigen Komponente der Theorie der
Elementarteilchen: die sogenannte Goldene Regel von Fermi.
4.3.1 Fermis Goldene Regel
Oft kann man Probleme nicht exakt lösen. Man braucht Näherungsmethoden.
Wir betrachten den folgenden Hamilton-Operator
H=
H
{0
zeitunabhängiger
ungestörter Hamilton −Operator
+
V
{
zeitabhängige
Störung
H0 entspricht dem ungestörten Hamilton-Operator und ist zeitunabhängig. Die Störung V ist im Allgemeinen zeitabhängig.
Wir nehmen an, dass die Eigenwerte und Eigenfunktionen des ungestörten Hamilton-Operators die folgenden sind
H 0 un = E n un
wobei un = Eigenzustand
Eine stationäre Lösung ist deshalb zu
r
e -iE n t un ( x )
58
Teilchenphysik II&III, WS 01/02-SS02, Prof. A. Rubbia
St rungstheorie
proportional.
Falls die |un> ein vollständiges System bilden, können wir
annehmen, dass eine Lösung von H als Linearkombination
der Eigenfunktionen von H0 ausgedrückt werden kann:
r
r
ψ ( x, t) = ∑ an ( t)e -iE n t un ( x )
n
Aus der Schrödinger-Gleichung folgt,
i
∂
ψ = Hψ
∂t
 dan

+ an E n  e -iE n t un =( H 0 + V ) ∑ an e -iE n t un

dt
n
∑  i
⇒
n
Mit H0|un>=En|un> erhalten wir
 dan  -iE n t
-iE t
 e un = ∑ anVe n un

dt
n
∑  i
n
Wir multiplizieren die Gleichung mit uf* und führen eine räumliche
Integration durch:
i∫ ∑
n
r
r
dan * -iE n t
u f e un d 3 x = ∫ ∑ an u*f Ve -iE n t un d 3 x
dt
n
oder
i∑
n
(
)
r
dan
d 3 xu*f un e -iE n t = ∑ an e -iE n t
∫
dt 14243
n
=δ
Teilchenphysik
(∫ d xur Vu )
3
*
f
n
n
f
59
Die nicht-relativistische Quantenmechanik
Die Zeitabhängigkeit des Koeffizienten af ist gegeben durch
i
da f -iE f t
e
= ∑ an e -iE n tV fn ( t)
dt
n
r
r
wobei V fn ( t) = ∫ d 3 xu*f V ( x, t) un
oder
da f
i E −E t
= −i ∑ an e ( f n ) V fn ( t)
dt
n
Wie wird diese Gleichung benutzt? Wir betrachten eine bestimmte
Anordnung: ein freies Teilchen bewegt sich im Raum. Zur Zeit t≈0
wirkt ein zeitabhängiges Potential V während eines kurzen Zeitintervalls.
Wir sind am Zustand des Teilchens nach der Potentialwirkung
interessiert.
Der Anfangszustand (zur Zeit –T/2) ist gleich
T
t=− :
2
  T
ai  − 2  = 1


a  − T  = 0
 n  2 
n≠i
d.h., das Teilchen befindet sich am Anfang im Zustand |ui>.
60
Teilchenphysik II&III, WS 01/02-SS02, Prof. A. Rubbia
St rungstheorie
Annahme: wenn die Störung klein ist, bleibt der Zustand ungefähr
im Anfangszustand. Es folgt,
da f
i E −E t
= −i ∑ an e ( f n ) V fn ( t)
dt
n
i( E f − E i ) t
V fi ( t)
≈ −ia{
i ( t)e
≈1
Diese Näherung wird als erste (oder Born’sche) Ordnung bezeichnet.
Durch Zeit-Integration erhalten wir
a f ( t) ≈ − i ∫
t
−T /2
dt′V fi ( t′ )e (
)
i E f − Ei t ′
Zur Zeit +T/2 wird der Endzustand durch den Koeffizient af(T/2)
definiert
+T / 2
r r
r
r i E −E t ′
T
a f   ≈ −i ∫
dt′ ∫ d 3 xu*f ( x )V ( x, t) ui ( x )e ( f i )
−T / 2
 2
Wir betrachten nun den Fall, in dem die Störung zeitunabhängig ist
und lassen T nach unendlich gehen:
r
r
V ( x, t) = V ( x ) und T → ∞
Die Übergangs-Amplitude vom Anfangszustand i in den Endzustand f wird definiert als
∞
r r
r
r
i E −E t ′
Tfi ≡ −i ∫ dt′e ( f i ) ∫ d 3 xu*f ( x )V ( x ) ui ( x )
−∞
Wir bemerken, dass die zeitliche Integration zu einer Dirac-δ-Funktion führt.
Teilchenphysik
61
Die nicht-relativistische Quantenmechanik
Dirac-δ-Funktion. Wir betrachten die Fouriertransformierte Funktion
f ( x) =
1
2π
∞
∫ A(k )e
ikx
1
2π
wobei A( k ) =
dk
−∞
∞
∫
f ( x )e − ikx dx
−∞
Es gilt,
1
f ( x) =
2π
=
∞
∞
∫ dke ∫ dyf ( y )e
ikx
−∞
− iky
−∞
∞
∞
−∞
−∞
dk
∫ dyf ( y ) ∫ 2π e
+ ik ( x − y )
∞
=
∫ dyf ( y )δ ( x − y )
−∞
und deshalb
δ ( x − y) =
∞
dk
∫ 2π e
+ ik ( x − y )
−∞
Mit der Dirac-δ-Funktion erhalten wir für die Übergangsamplitude
(
Tfi = −iV fi (2π )δ E f − E i
)
Wir bemerken, dass die Übergangs-Amplitude verschwindet, wenn
die Anfangs- und Endzustandsenergien nicht gleich sind:
Tfi = 0 wenn E f ≠ E i
d.h., eine zeitunabhängige Störung kann die Energie des Teilchens
nicht ändern.
62
Teilchenphysik II&III, WS 01/02-SS02, Prof. A. Rubbia
St rungstheorie
Die Übergangswahrscheinlichtkeit pro Zeiteinheit wird definiert
als
W ≡ lim
Tfi
T →∞
2
T
wobei wir den Betrag im Quadrat der Amplitude verwendet haben.
Durch Einsetzen erhalten wir
W = lim
(
−iV fi (2π )δ E f − E i
T →∞
)
2
T
(
)
1
1 T /2
2
i E −E t
V fi (2π ) δ E f − E i
dte ( f i )
∫
2
−
/
T
T →∞ T
2π
/2
T
2
1
= lim V fi (2π )δ E f − E i ∫ dt
−T2
/ 23
T →∞ T
1
= lim
2
(
)
=T
Die Übergangswahrscheinlichkeit pro Zeiteinheit ist deshalb gleich
2
(
W = (2π ) V fi δ E f − E i
)
Wir können nun annehmen, dass das Teilchen einen Übergang in
viele Endzustände mit der Energie Ef machen kann. Wir führen die
Dichte der Endzuständen ρ ein als:
ρ( E f ) dE f = Anzahl der Endzustände
im Energieintervall E f und E f + dE f
Teilchenphysik
63
Die nicht-relativistische Quantenmechanik
Die gesamte Übergangswahrscheinlichtkeit pro Zeiteinheit vom
Zustand i zu Zuständen f wird durch Intergration über die möglichen
Endzustände gewonnen:
2
(
)
W fi = (2π ) ∫ dE f V fi δ E f − E i ρ( E f )
2
= (2π ) V fi ρ( E f )
Fermis Goldene Regel
4.3.2 Elastisches Streuexperiment
Wir versuchen nun ein Streuexperiment mit Hilfe der quantenmechanischen Beschreibung zu analysieren.
Wir vereinfachen das Problem und betrachten nur elastische Stösse
an einem festen Potential.
In dieser Beschreibung ist ein Potential V für die Streuung des Teilchens verantwortlich. Als Folge wird das Teilchen seinen Impuls
ändern. Im elastischen Stoss wird der Betrag des Impulses nicht
geändert, nur die Richtung:
r
r
r
pi = p f = p = p
Die Streuung wird als ein Übergang vom Anfangszustand mit
Impuls pi zum Endzustand mit Impuls pf dargestellt.
Siehe Abb. 1.
64
Teilchenphysik II&III, WS 01/02-SS02, Prof. A. Rubbia
St rungstheorie
pf
θ
pi
V
Figur 1.
Streuexperiment in der quantenmechanischen Beschreibung
Vergleiche mit Abb. 5 im Kap. 1.4.1.
In der quantenmechanischen Beschreibung spricht man nicht
mehr von der Bahnkurve des Teilchens, wir sind an der Übergangswahrscheinlichkeit zwischen Zuständen mit bestimmten Impulsen pi → pf interessiert.
Einfallendes Teilchen: ebene Welle mit bestimmtem Impuls pi, und
mit Normierung in einem Kasten des Volumens L3:
r
1 r r
ui ( x ) = 3 / 2 e ip i ⋅x
L
Teilchenphysik
r
Impuls pi
65
Die nicht-relativistische Quantenmechanik
Auslaufendes Teilchen:
r
1 ipr ⋅xr
u f ( x ) = 3/2 e f
L
r
Impuls p f
Der differentielle Wirkungsquerschnitt für den Übergang zwischen
Zuständen pi und pf wird definiert als
dσ ij ≡
W fi
j
wobei j = Fluss des einfallenden Teilchens
Einheit: Wfi = Übergangwahrscheinlichtkeit pro Zeiteinheit
j=Wahrscheinlichkeit pro Zeitheinheit und Flächeneinheit
d.h. der Wirkungsquerschnitt hat, wie erwartet, die Einheit einer Fläche.
Für ein freies einfallendes Teilchen ist der Fluss gleich (Siehe
Kap. 4.1.4)
r
r
1 p
2 p
⇒ j= 3
j= N
m
L m
Es folgt daraus mit Fermis Goldener Regel:
2
2
W fi (2π ) V fi ρ( E f )
mL3
dσ ij ≡
=
= (2π )
V fi ρ( E f )
1 p
j
p
L3 m
66
Teilchenphysik II&III, WS 01/02-SS02, Prof. A. Rubbia
St rungstheorie
Wir bestimmen die Dichte der Endzustände. Für eine ein-dimensionale Anordnung, erhalten wir
u f ( x ) = Ne
ip f ⋅ x
⇒ dp f =
⇒ u f ( L) = Ne
ip f ⋅ L
=1 ⇒
pf =
2πn
L
2π
dn
L
und in 3 Dimensionen
3
3
 L
 L
dn =   dpx dpy dpz =   p 2 dpdΩ
 2π 
 2π 
Die Dichte der Zustände ist
dn
ρ( E f ) =
dE f
pdp
p2
1
wenn E f =
2 pdp =
⇒ dE f =
m
2m
2m
oder
3
 L 2
  p dpdΩ
3
dn  2π 
 L
ρ( E f ) =
=
=   mpdΩ
pdp
 2π 
dE f
m
Der differentielle Wirkungsquerschnit wird dann gegeben durch
dσ = (2π )
Teilchenphysik
3
2
2 L 
2
mL3
 m
V fi   mpdΩ =   L6 V fi dΩ
 2π 
 2π 
p
67
Die nicht-relativistische Quantenmechanik
oder
2
dσ  m  6 2
=   L V fi
dΩ  2π 
Das Matrix-Element Vfi wird bestimmt:
r
r
r − ipr ⋅xr r r r 1
r r rr
1
V fi = ∫ d 3 xu*f V ( x ) ui = 3 ∫ d 3 xe f V ( x )e ip i ⋅x = 3 ∫ d 3 xV ( x )e iq ⋅x
L
L
wobei
r r r
q ≡ pi − p f = Aenderung des Impulses
Man spricht vom Impulsübertrag q. Schliesslich wird der Wirkungsquerschnitt geschrieben als
dσ  m 
= 
dΩ  2π 
2
r iqr ⋅xr 2
3r
(
)e
d
xV
x
∫
Diese Gleichung entspricht dem differentiellen Wirkungsquerschnitt
für die Streuung am Potential V. Diese Gleichung gilt in erster Näherung (der sogenannten Born’schen Näherung).
4.4 Rutherford-Streuung
Wir betrachten nun die Anordnung des Rutherford-Streuexperiments.
In der Störungstheorie muss das Potential schwach sein.
Wir können kein Potential verwenden, das eine unendliche Reichweite wie die Coulomb-Kraft besitzt. Wir nehmen deshalb an, dass
68
Teilchenphysik II&III, WS 01/02-SS02, Prof. A. Rubbia
Rutherford-Streuung
die Ladung des punktförmigen Kerns von einer Elektronenwolke
abgeschirmt wird.
D.h., für das Potential verwenden wir ein Coulomb-Potential für eine
punktförmige Ladung +Ze, korrigiert für eine Elektronenwolke der
Ladung –Ze:
r
r
ze 2  Z
ρ( x ′ ) 3 r 
(
)
≡
−
V x
r r d x ′
 r
4πε 0  x ∫ x − x ′

wobei
r
∫ ρ( x ′)d
3
r
x′ = Z
der gesamten Ladung der Elektronen entspricht. In der letzten Gleichung haben wir angenommen, dass das Atom elektrisch neutral ist.
Die Ladung des gestreuten Teilchens ist gleich ze.
In erster Born’scher Näherung müssen wir das folgende Integral
berechnen, um das Matrix-Element zu bestimmen:
r
r iqr ⋅xr
ze 2
ρ( x ′ ) 3 r  iqr ⋅xr
3r
3 r Z
∫ d xV ( x )e = 4πε 0 ∫ d x  xr − ∫ xr − xr ′ d x ′ e
Wir bemerken, dass
r 2 iqr ⋅xr
r iqr ⋅xr
2
3r
3r
∫ d xV ( x )(∇ e ) = (iq) ∫ d xV ( x )e
Es folgt,
r iqr ⋅xr
r 2 iqr ⋅xr
1
3r
3r
d
xV
(
x
)
e
=
−
d
xV
(
x
)(∇ e )
∫
q2 ∫
Teilchenphysik
69
Die nicht-relativistische Quantenmechanik
Mit Hilfe des Satzes von Green (Siehe Übungen) erhalten wir
r 2 iqr ⋅xr
3r
(
)(∇ e ) =
d
xV
x
∫
r iqr ⋅xr
r
r r
r r r
r
3 r iq ⋅ x
2
iq ⋅ x
+
∇
−
∇
∇
(
)
d
xe
V
x
V
e
e
V
dA
(
)
∫
∫
A =∂V
((
)
( ))
Das Integral über die Fläche A, die das Volumen V umschliesst, verschwindet, wenn das Volumen nach unendlich geht, da gilt
r
r
V ( x ) → 0 wenn x → ∞
r r
r
∇V ( x ) → 0 wenn x → ∞
Durch Ersetzen von V können wir den Laplace-Operator, angewendet
auf das Potential, berechnen
r
ze 2  2  1 
1  r 3r 
2
∇ V (x) =
∇
−
∇
Z
r
r
r  ρ( x ′ ) d x ′



4πε 0 
 x  ∫  x − x′ 

2
Aus dem Elektromagnetismus (Siehe z.B. Jackson) kennen wir die
Beziehung
 1 
r r
∇ 2  r r  = −4πδ ( x − x ′ )
 x − x′ 
Deshalb ist
r
r
r
ze 2
∇ V (x) = −
Zδ ( x ) − ρ( x ))
(
ε0
2
70
Teilchenphysik II&III, WS 01/02-SS02, Prof. A. Rubbia
Rutherford-Streuung
Das Integral des Potentials ist deshalb gleich
∫d
3
r r
r r rr
r r
1
xV ( x )e iq ⋅x = − 2 ∫ d 3 xV ( x )(∇ 2e iq ⋅x )
q
r rr
r
1
= − 2 ∫ d 3 xe iq ⋅x (∇ 2V ( x ))
q
=
r r
r
r
ze 2 1
3 r iq ⋅ x
d
xe
Zδ ( x ) − ρ( x ))
(
2 ∫
ε0 q
Dieses Integral besitzt zwei Teile, die wir in folgender Weise ausdrücken werden:
r r iqr ⋅xr ze 2 1
r
∫ d xV ( x )e ≡ ε 0 q2 [Z − F (q )]
3
wobei F(q) die Fouriertransformierte der Elektronenladungsverteilung ist:
r
r rr r
F (q ) ≡ ∫ d 3 xe iq ⋅x ρ( x )
Schliesslich ist der Wirkungsquerschnitt gleich
2
2
r 2
dσ  m   ze 2   1 
=      4  [ Z − F (q )]
dΩ  2π   ε 0   q 
wobei der Impulsübertrag gleich
r r r
q ≡ pi − p f = Aenderung des Impulses
ist. Wir können den übertragenen Impuls q als Funktion des Streuwinkels ausdrücken:
Teilchenphysik
71
Die nicht-relativistische Quantenmechanik
r r r
q ≡ pi − p f
r
r
r
r r
⇒ q 2 ≡ pi 2 + p f 2 − 2 pi ⋅ p f = 2 p 2 − 2 p 2 cosθ
r
q 2 = 2 p 2 (1 − cosθ ) = 4 p 2 sin 2 (θ / 2)
Es folgt, wie erwartet
r
q 2 → 0 wenn θ → 0
In diesem Fall kann man die Fouriertransformierte durch die ersten
Glieder ihrer Taylor-Reihe approximieren:
r r
r r 1 r r 2
e iq ⋅x ≈ 1 + iq ⋅ x + (iq ⋅ x ) + ...
2
D.h.,
r
r rr r
Z − F (q ) = Z − ∫ d 3 xe iq ⋅x ρ( x )
r r
r r r r 1
r r r 2 r
= Z − ∫ d 3 xρ( x ) − i ∫ d 3 x (q ⋅ x ) ρ( x ) + ∫ d 3 x (q ⋅ x ) ρ( x ) + ...
2
14
4244
3 1442r443
r
=0
=
= 0 wenn ρ ( x )= ρ ( − x )
1 3r r r 2 r
d x (q ⋅ x ) ρ( x ) + ...
2∫
Das Ergebnis hängt von der Verteilung der Ladung ab. Im Allgemeinen gilt
r 1
Z − F (q ) = q 2
2
(
)
r
r 2 r
q2I
∫ d x (q√⋅ x ) ρ( x ) = 2
3
wobei I dem Integral entspricht, das von der Ladungsverteilung
abhängt.
72
Teilchenphysik II&III, WS 01/02-SS02, Prof. A. Rubbia
Rutherford-Streuung
D.h., für kleine Streuwinkel gilt
2
2
2
r
 dσ 
 m   ze   1 
= 
 
[Z − F (q )]2
 dΩ θ →0  2π   ε 0   q 4 
2
2
2
2
 m   ze   1   q I 
≈      4  
 2π   ε 0   q   2 
2
2
2
2
2
 m   ze   I 
≈       ≈ konst.
 2π   ε 0   2 
Dank der Verteilung der Elektronenwolke gibt es keine Divergenz,
wenn der Streuwinkel nach null geht. Wenn der Streuwinkel nach null
geht, ist der Grenzwert des Wirkungsquerschnitt gleich einer Konstanten.
Was passiert, wenn der Betrag des übertragenen Impulses q gross ist?
Wir erwarten, dass gilt
r
r
F (q ) → 0 wenn q → ∞
weil die Elektronenwolke nicht in einem Punkt konzentriert ist. Die
Elektronenwolke ist keine Punktladung, und deshalb wird die Fouriertransformierte Funktion verschwinden, wenn der Betrag des
“Wellenvektors” q nach unendlich geht.
Für einen genügend grossen Betrag des übertragenen Impulses wird
es möglich sein, F(q) im Vergleich zu Z zu vernachlässigen.
Teilchenphysik
73
Die nicht-relativistische Quantenmechanik
In diesem Fall gilt
2
2
2
r 2
 dσ 
 m   ze   1 
=      4  [ Z − F (q )]
 
 dΩ qr →∞  2π   ε 0   q 
2
2
2
 m   zZe   1 
≈  
 2π   ε 0   q 4 
2
 zZe 2  

2m
=
  2 2

 4πε 0   4 p sin (θ / 2) 
2
2
 zZe 2   1  2
1
 dσ 
= 
=

 
4
 4πε 0  4 E  sin (θ / 2)  dΩ Rutherford
Dieses Ergebnis ist gleich dem der klassischen Herleitung. Vergleiche
mit Kap. 1.4.1.
Der Rutherford-Wirkungsquerschnitt stellt deshalb die Born’sche
Näherung dar, wenn der übertragene Impuls oder der Streuwinkel
nicht zu klein ist, und wir in diesem Fall den Effekt der Elektronenwolke vernachlässigen können.
74
Teilchenphysik II&III, WS 01/02-SS02, Prof. A. Rubbia