Zahlenbereichserweiterungen - Mathematik in der Sekundarstufe 1

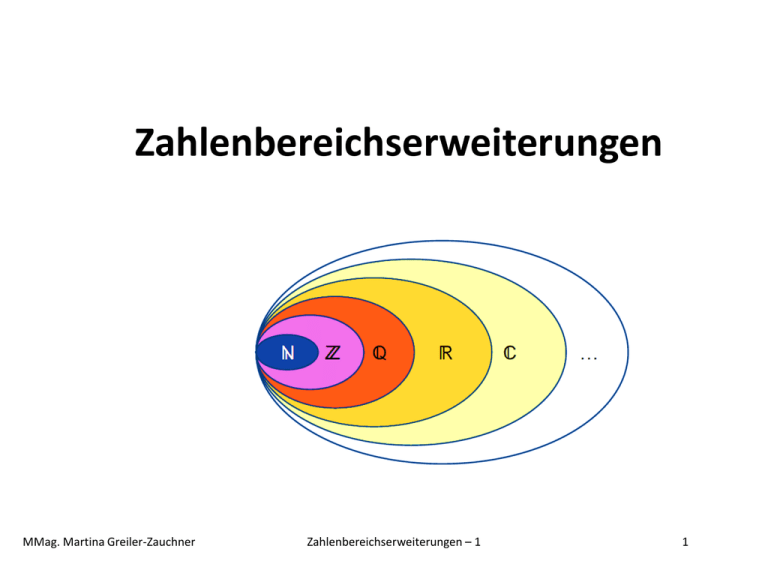
Zahlenbereichserweiterungen
MMag. Martina Greiler-Zauchner
Zahlenbereichserweiterungen – 1
1
Literatur (Teil 1-allgemeiner Teil)
1. Andreas ULOVEC, Wenn sich Vorstellungen wandeln – Ebenen der
Zahlenbereichserweiterungen, in: mathematiklehren 142 (2007) S14ff
2. Lisa Hefendehl-Hebeker und Susanne Prediger, Unzählig viele Zahlen: Zahlbereiche
erweitern – Zahlvorstellungen wandeln
in: Praxis der Mathematik in der Schule 48 (2006)11, S. 1ff
Link
3. Jürgen Roth, Didaktik der Zahlenbereichserweiterungen
http://www.dms.unilandau.de/roth/lehre/skripte/did_zahlbereichserweiterungen/did_zahlbereichserweit
erungen_2_natuerliche_zahlen.pdf
MMag. Martina Greiler-Zauchner
Zahlenbereichserweiterungen – 1
2
Exkurs: Historisches zu den Zahlen
Die Methode des Zählens zur Bestimmung der Größe einer Gesamtheit (etwa einer
Mammutherde) ist sicherlich so alt wie die Menschheit. Mit Entwicklung der Schrift
wurden auch Zahlzeichen (Ziffern) eingeführt, die meistens auf dem Dezimalsystem
beruhen und größere Zahlen durch Zusammenfassung darstellen. Der Grund dafür ist
offenbar in der Anzahl der Finger zu suchen. Das englische Wort digit für Ziffer stammt
vom lateinischen digitus (Finger) ab und man kann vermuten, dass die sprachliche
Verwandtschaft des Zahlwortes „zehn“ mit „Zehen“ kein Zufall ist. Die bis heute
üblichen Ziffern 0,1,…,9 sind um 400 v. Chr. in Indien entstanden., wobei das Symbol 0
zunächst nicht für eine Zahl stand, sondern nur als Hilfsmittel in Zusammensetzungen
wie 201 Sinn machte. Die Null als Zahl sowie die negativen ganzen Zahlen wurden erst
einige Jahrhunderte später einbezogen.
Reiss, K. & Schmieder, G. (2005). Basiswissen Zahlentheorie.
Heidelberg: Springer.
MMag. Martina Greiler-Zauchner
Zahlenbereichserweiterungen – 1
3
Exkurs: Historisches zu den Zahlen
Entwicklung unserer heutigen Ziffernsymbole
MMag. Martina Greiler-Zauchner
Zahlenbereichserweiterungen – 1
4
Die natürlichen Zahlen
Die Menge ℕ der natürlichen Zahlen umfasst die natürlichsten Zahlen, nämlich jene,
die beim Zählen von Gegenständen begegnen. Konkret handelt es sich dabei um
folgende Menge: ℕ={0,1,2,3,...}
Bis ins 19. Jahrhundert wurde versucht, den Zahlbegriff auf den psychologischen
Vorgang des Zählens zurückzuführen.
Die axiomatische Darstellung der natürlichen Zahlen durch G. Peano (italienischer
Mathematiker, 1858 – 1932) präzisiert und verallgemeinert die intuitive Vorstellung
von den Eigenschaften der natürlichen Zahlen!
Es sieht wie folgt aus:
Die natürlichen Zahlen sind eine Menge, für die gilt:
Peano Axiome (vereinfacht)
• 0 ist eine natürliche Zahl.
• Jede natürliche Zahl n hat eine natürliche Zahl n` als Nachfolger.
• 0 ist kein Nachfolger einer natürlichen Zahl.
• Natürliche Zahlen mit gleichem Nachfolger sind gleich.
• Induktionsprinzip! Enthält eine Menge M die 0 und mit jeder natürlichen Zahl n
auch deren Nachfolger n`, so bilden die natürlichen Zahlen eine Teilmenge von M.
MMag. Martina Greiler-Zauchner
Zahlenbereichserweiterungen – 1
5
Aspekte natürlicher Zahlen Kardinalzahlen
Die verschiedenen Aspekte der Verwendung von natürlichen Zahlen in
der Alltagswelt sollen ständig die Erarbeitung der Zahlbereiche
begleiten.
1. Verwendung als Kardinalzahl
Idee: Zahlen beschreiben die Mächtigkeit von Mengen, also die Anzahl
der Elemente.
• Das Seminar wird von 27 Teilnehmerinnen und Teilnehmern besucht.
• Martina hat 2 Brüder.
• Der Parkplatz bietet Parkmöglichkeiten für 120 Fahrzeuge.
Frage: Wie viele?
MMag. Martina Greiler-Zauchner
Zahlenbereichserweiterungen – 1
6
Aspekte natürlicher Zahlen Ordinalzahlen
2. Verwendung als Ordinalzahl
Idee: Gibt den Rangplatz eines Elementes in einer geordneten Reihe an
• Heute ist das erste Seminar zum Thema „Didaktik der Zahlbereiche“.
• Lena steht an dritter Stelle in der Warteschlange.
• Michael hat den fünften Platz im Marathonlauf erreicht.
Frage: Der/die/das Wievielte?
ODER
Idee: Folge der natürlichen Zahlen, die beim Zählen durchlaufen wird (durch
Zählzahlen wird auch Reihenfolge beschrieben)
• Im Buch bin ich auf Seite 34
• Das Haus mit der Nummer 14
MMag. Martina Greiler-Zauchner
Zahlenbereichserweiterungen – 1
7
Aspekte natürlicher Zahlen Maßzahlen
3. Verwendung als Maßzahl
Idee: Zahlen sind Maßzahlen in Größenangaben
•
•
•
•
Die Vorlesung dauert 90 Minuten.
5 kg Äpfel kosten 2,49 €.
Der Bahnhof ist 4 km vom Hauptgebäude der Universität entfernt.
Die Höchstgeschwindigkeit des Autos liegt bei 195 km/h.
Mögliche Fragen: Was kostet? Wie lange? Wie groß?
MMag. Martina Greiler-Zauchner
Zahlenbereichserweiterungen – 1
8
Aspekte natürlicher Zahlen Operatoren
4. Verwendung als Operatoren
Idee: Zahlen beschreiben die Vielfachheit einer Handlung oder eines Vorgangs
• Das Medikament muss 3mal täglich genommen werden.
• Die Vorlesung findet 2mal in der Woche statt.
• Mit einem Abonnement kommt man 6mal in der Saison in die Oper.
Frage: Wie oft?
MMag. Martina Greiler-Zauchner
Zahlenbereichserweiterungen – 1
9
Die Behandlung der Zahlenbereiche
im Mathematikunterricht
„Der Aufbau des Zahlensystems von den natürlichen bis zu den komplexen Zahlen
ist eine Kulturleistung von höchster Perfektion, die im Unterricht der
Sekundarstufe durch sukzessive Erweiterung der Zahlbereiche nachvollzogen wird.
Aus der Perspektive der Lernenden zeigen sich dabei Herausforderungen und
Hürden, die nur durch gewandelte Zahlvorstellungen zu überwinden sind!“
Aus: Unzählig viele Zahlen:
Zahlbereiche erweitern – Zahlvorstellungen wandeln
Lisa Hefendehl-Hebeker und Susanne Prediger
Praxis der Mathematik in der Schule 48 (2006)11, S. 1-7
MMag. Martina Greiler-Zauchner
Zahlenbereichserweiterungen – 1
10
Anlässe für Zahlenbereichserweiterungen
Aus: Unzählig viele Zahlen:
Zahlbereiche erweitern – Zahlvorstellungen wandeln
Lisa Hefendehl-Hebeker und Susanne Prediger
Praxis der Mathematik in der Schule 48 (2006)11, S. 1-7
MMag. Martina Greiler-Zauchner
Zahlenbereichserweiterungen – 1
11
Probleme bei den
Zahlenbereichserweiterungen
Mit neuen Zahlenbereichen sind aber auch oft Verluste im Vergleich zum
alten Zahlenbereich verbunden.
Zitat:
„Wir rechnen jetzt auch mit Minuszahlen. Die sind eigentlich ganz okay, aber
manchmal ziemlich komisch.
Guck mal, da soll –10 weniger sein als -4, das haben sich die Mathe-Lehrer
echt seltsam ausgedacht. Warum ist das nicht wie bei den normalen Zahlen?
Deswegen mach ich das manchmal auch andersrum, das ist dann falsch...“
oder
- Subtraktion verkleinert, aber : (-5)-(-7)=2
- Ordnungsverlust von ℝ auf ℂ
- Eindeutigkeit zwischen Zahl und Zahlzeichen geht von ℕ auf ℚ verloren
- ….
MMag. Martina Greiler-Zauchner
Zahlenbereichserweiterungen – 1
12
Hürden bei den Dezimalzahlen
MMag. Martina Greiler-Zauchner
Zahlenbereichserweiterungen – 1
13
3 Ebenen der
Zahlenbereichserweiterungen
• Mathematisch-formale Ebene:
Natürliche Zahlen: Peano-Axiome
Bruchzahlen: sind Äquivalenzklassen geordneter Paare
-> andere LV
• Darstellungsebene:
• Vorstellungsebene:
MMag. Martina Greiler-Zauchner
Zahlenbereichserweiterungen – 1
14
Darstellungsebene
Kontinuitäten und Diskontinuitäten
Zahldarstellung
Natürliche
Zahlen ℕ
Bruchzahlen
ℚ+
Ganze
Zahlen ℤ
Rationale Zahlen
ℚ
Reelle
Zahlen ℝ
Komplexe
Zahlen ℂ
Eindeutig
(z.B.: 134)
Unendlich vieldeutig
1
2
3
(z.B.: = = )
2
4
6
In Dezimaldarstellung:
0,576….eindeutig, wenn
unendlich viele
Nachkommastellen und
Periodizität zugelassen
sowie unendliche
Neunerperioden
ausgeschlossen werden
Eindeutig
(z.B.: -134)
Unendlich vieldeutig
1
2
3
(z.B.: − = − = − )
2
4
6
In Dezimaldarstellung:
-0,576….eindeutig, wenn
unendlich viele
Nachkommastellen und
Periodizität zugelassen
sowie unendliche
Neunerperioden
ausgeschlossen werden
Nicht eindeutig
(z.B.:
4
2 = 16 )
Nicht endlich
darstellbar
außer als
Symbol
( 2, 𝑒, 𝜋)
Eindeutig im
Sinne von
a+bi=c+di,
wenn a=c und
b=d, aber
Darstellung von
a und b nicht
eindeutig (wie
in ℝ )
Aus mathematiklehren 142
Wenn sich Vorstellungen wandeln
von Andreas Ulovec
S15
MMag. Martina Greiler-Zauchner
Zahlenbereichserweiterungen – 1
15
Vorstellungsebene
Übergang von den natürlichen Zahlen zu den Bruchzahlen
Kontinuitäten und Diskontinuitäten
Natürliche Zahlen
Bruchzahlen
Grundvorstellungen
(inhaltliche Vorstellungen)
zu Zahlen
Zahlen werden aufgefasst als:
• Kardinalzahl
• Ordinalzahl
• Maßzahl
• Operator
Zahlen werden aufgefasst als:
• Bruch als Teil eines Ganzen
• Bruch als relativer Anteil
• Bruch als Resultat einer Division
• Bruch als Verhältnis
• … (siehe Kapitel 2)
Ordnungsrelation
Jede Zahl hat einen eindeutigen Nachfolger
Keinen unmittelbaren Nachfolger
(abgeschwächt: für jede Bruchzahl existiert eine größere
Bruchzahl)
rechnerische Ausführung schwieriger als
Interpretation
Grundvorstellungen für
Operationen
Addition: Hinzufügen, Zusammenfügen
Addition und Subtraktion bleiben der Vorstellung
nach gleich, der Einfachheit der Vorstellung entspricht
keine vergleichbare Einfachheit der Durchführung
Subtraktion: Wegnehmen, Vermindern
Multiplikation: Abgekürzte Addition, „von“Deutung (Vierfaches von 3), Streckung
Division: (Ver)teilen, Aufteilen
MMag. Martina Greiler-Zauchner
Zahlenbereichserweiterungen – 1
Multiplikation und Division mit eingeschränkten und
modifizierten Interpretationen:
„von“ Deutung
Streckung und Stauchung
Multiplikation vergrößert nicht immer
16
Grundvorstellungen zu Bruchzahlen
OperatorVorstellung
(Bruch als
multiplikative
Rechenanweisun
g): Der Gewinn
3
beträgt 4 von 120
Euro
(Rechenoperation
wird auf dem
Bruch
angewendet).
MMag. Martina Greiler-Zauchner
3
4
AnteilsVorstellung
(Bruch als Teil
eines Ganzen,
als Teil mehrerer
3
Ganzer): 4 von
einer Pizza oder
von 3 Pizzen.
Verhältnis-Vorstellung (Bruch als
(Mischungs-) Verhältnis: Apfelsaft und
Wasser werden im Verhältnis 3:4 gemischt.
Zahlenbereichserweiterungen – 1
17
Vorstellungsebene
Übergang zu den Negative Zahlen
Kontinuitäten und Diskontinuitäten
Negative Zahlen
Grundvorstellungen zu
Zahlen
relative Zahlen bezüglich einer fest gewählten Vergleichsmarke
Maßzahl
Richtungen
Gegensätze
Ordnungsrelation
Jede Zahl hat einen eindeutig bestimmten unmittelbaren Nachfolger (auch Vorgänger)
Die Begriffe „mehr“ und „weniger“ sind neu deutungsbedürftig
leitende Idee für Ordnungsrelation:
Orientierung der Zahlengerade
Grundvorstellungen für
Operationen
Addieren und Subtrahieren:
Die Grundvorstellung des Zusammenfügens und Hinzufügens muss modifiziert werden.
(Fügt man zu -2€ Schulden -4€ Schulden hinzu!)
Hinzufügen ist nicht stets Vermehren!
Wegnehmen ist nicht stets Vermindern!
Multiplizieren und Dividieren:
Grundvorstellung von Multiplizieren als abgekürzte Addition ist nur mehr ein Spezialfall
„Von“-Deutung muss aufgegeben werden (Das -4-fache von 3)
Deutung als Streckung: Auch Richtungsumkehr möglich
MMag. Martina Greiler-Zauchner
Zahlenbereichserweiterungen – 1
18
Vorstellungsebene
Übergang zu den Reellen Zahlen
Kontinuitäten und Diskontinuitäten
Reelle Zahlen
Grundvorstellungen zu
Zahlen
Grundvorstellungen ergeben sich aus Konstruktion der beliebig genauen Näherung
globale Sicht: geschlossene Lücken auf der Zahlengerade (Vollständigkeit)
Ordnungsrelation
Keine unmittelbaren Nachfolger bzw. Vorgänger!
Grundvorstellungen für
Operationen
keine neuen Grundvorstellungen nötig
Da Unterricht selten zu grundlegenden Fragen vordringt (etwa: wie addiert man nicht
abbrechende Dezimalzahlen?), werden hier selten Probleme erlebt.
MMag. Martina Greiler-Zauchner
Zahlenbereichserweiterungen – 1
19
Vorstellungsebene
Übergang zu den Komplexen Zahlen
Kontinuitäten und Diskontinuitäten
Komplexe Zahlen
Grundvorstellungen zu Zahlen
Zahlen als
• Zahlenpaare (a,b) oder (r,𝞿)
• formal als Lösung einer Gleichung
Ordnungsrelation
Keine Ordnung
Grundvorstellungen für Operationen
Operationen mit Punkten und Pfeilen
(geometrisch)
MMag. Martina Greiler-Zauchner
Zahlenbereichserweiterungen – 1
20
Workload
Lit:
Zahlen fallen nicht vom Himmel
Ein Blick in die Geschichte der Mathematik
Aus: ml142
Kapitel:
- Ein didaktischer Blick auf historische Zahlbereichserweiterungen
- Entstehung der Bruchzahlen aus den natürlichen Zahlen
Fassen Sie die Inhalte der Kapitel zusammen und recherchieren Sie zum Inhalt, falls es
Unklarheiten und Probleme bezüglich Verständnis gibt!
MMag. Martina Greiler-Zauchner
Zahlenbereichserweiterungen – 1
21