b−U a=−∫a F⋅d s=−q∫a E⋅d s

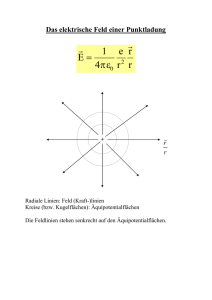
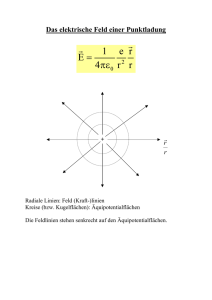
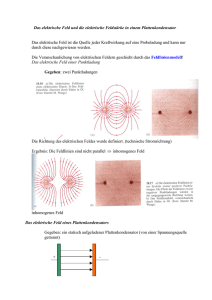
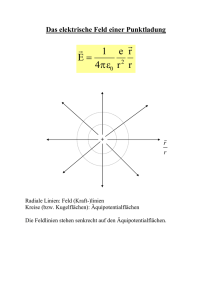
3 – Elektrisches Potential
In der Mechanik hat sich das Energiekonzept als äußert wertvoll für die Lösung von Problemen erwiesen. Ein Grund dafür ist, dass Energie eine Erhaltungsgröße ist. Es lassen sich damit Aufgaben lösen, für die eine detaillierte Angabe aller wirkenden Kräfte gar nicht möglich ist. Auch im elektrischen Fall erweist sich der Energieansatz als sehr nützlich. Er führt uns auf den Potentialbegriff.
3.1 – Elektrisches Potential und Potentialdifferenz
Die durch das Coulomb­Gesetz ausgedrückte Kraft zwischen Ladungen ist konservativ, d.h. sie impliziert keine Reibungsterme. Für konservative Kräfte kann stets eine potentielle Energie U definiert werden.
Wir definieren zunächst:
Die Änderung der potentiellen Energie Ub – Ua bei der Verschiebung einer Ladung q
im elektrischen Feld von Punkt a nach Punkt b entspricht dem Negativen der vom Feld
an der Ladung geleisteten Arbeit:
b
b
⋅d s
U b −U a =−∫a F⋅d s =−q ∫a E
Analog zur Einführung des elektrischen Feldes als Kraft pro Einheitsladung wird das
elektrische Potential V als die potentielle Energie pro Einheitsladung definiert.
Besitzt eine Testladung an einem Punkt a bezüglich eines beliebigen Referenzpunktes die potentielle Energie Ua, so ist ihr Potential am Punkt a:
V a=
Ua
q
Nur die Differenz zweier Potentiale ist physikalisch bedeutsam, denn nur sie ist messbar.
Für die Potentialdifferenz gilt demgemäß:
V ba =V b −V a =
U b −U a
q
=−
W ba
q
Die Einheit des Potentials und der Potentialdifferenz ist das Volt ( 1 V = 1 J/C ) zu Ehren von Alessandro Volta (1745­1827).
Der Begriff Spannung ist Synonym zum Begriff Potentialdifferenz.
Wenn wir vom Potential an einem Punkt a reden, müssen wir uns auf einen Bezugspunkt festlegen. Das geschieht je nach Problem nach dem Zweckmäßigkeitsprinzip.
Einige typische Spannungswerte
Quelle
ca. Spannung in Volt
Gewitterwolke gegen Erde
108
Hochspannungsleitung
106
Hochspannungsversorgung in TV
104
Zündspule im Auto
104
Steckdose
102
Autobatterie
12
Mignon­Zelle
1.5
Ruhepotential über Nervenzellmembran
10­1
Potentialänderungen an Hautoberfläche (EKG, EEG)
10­4
3.2 – Zusammenhang zwischen elektrischem Potential und elektrischem Feld
Die Auswirkungen von Ladungsverteilungen können sowohl durch das elektrische Feld, als auch durch das Potential beschrieben werden. In der Regel ist das Potential einfacher zu behandeln, weil es eine skalare Größe ist.
Wir haben das Potential über die potentielle Energie eingeführt. Damit können wir sofort einen Zusammenhang zwischen Vba und E feststellen:
V ba =V b − V a =−
1 b
F⋅d s 
∫
a
q
b
⋅d s
V ba =−∫a E
Kennen wir also das elektrische Feld als Folge einer Ladungsverteilung, so können wir über dieses Integral die Potentialdifferenz zwischen zwei Punkten a und b bestimmen.
Den umgekehrten Zusammenhang Vba  E lernen wir später kennen. Er wird uns zum Differentialoperator  = (/x, /y, /z) führen.
Das homogene Feld stellt einen einfachen Spezialfall dar. Es gilt dann für die Potentialdifferenz zwischen zwei Punkten a und b im Abstand d entlang der Feldlinien:
b
  r =E
  V =−∫ E
⋅d s =−E d
E
ba
a
V ba =−Ed
Offensichtlich ist die Einheit des elektrischen Feldes auch 1 V/m, denn das ist gleich 1 N/C.
3.3 – Elektrisches Potential von Punktladungen
Das elektrische Potential im Abstand r von einer Punktladung Q erhalten wir durch direkte Anwendung des Integralausdrucks aus 3.2:
rb
V b −V a =−∫r
a

r 1
Q Q
Q
1

E⋅d s =−
dr
=
−
∫
4  0 r r 2
4  0 r b r a
b
a

Da wir bezüglich der Wahl des Bezugspunkts unserer Potentialdifferenz freie Wahl haben, setzen wir zweckmäßigerweise ra = .
Damit ist das Potential im Abstand r von einer Punktladung:
V r =
1 Q
4  0 r
Mit diesem Bezugspunkt ra =  können wir V(r) als das absolute Potential betrachten, oder eben auch als die Potentialdifferenz zwischen r und .
Wir halten fest:
Das Potential einer Punktladung fällt wie 1/r mit dem Abstand r ab.
● Es ist positiv für eine positive Punktladung und negativ für eine negative Punktladung
●
Die Bestimmung des elektrischen Feldes in Gegenwart einer Verteilung von Punktladungen kann schnell kompliziert werden, da die Vektorsumme der Einzelfelder gebildet werden muss.
Das elektrische Potential zu finden ist dagegen viel einfacher. Es sind nur Skalare Felder zu addieren. Wir müssen allerdings auf die Vorzeichen der Ladungen achten.
Hörsaal­Übung: Wie groß ist das Potential an den Punkten A und B in der Abbildung
für die gegebene Ladungsverteilung von zwei Punktladungen?
A
d
B
D
d
Q1 = Q > 0
Q1 = ­Q < 0
Diese einfache Art der Summation funktioniert ebenso für beliebig viele Punktladungen. Eine Möglichkeit, aus einem so berechneten Potential das elektrische Feld zu bestimmen, wäre deshalb sehr praktisch. Diese gibt es, wie erwähnt. Dazu später mehr.
3.4 – Elektrisches Potential beliebiger Ladungsverteilungen
Wir hatten bereits diskutiert, wie sich das elektrische Feld einer beliebigen Ladungsverteilung bestimmen lässt. Insbesondere wurden wir für kontinuierliche Ladungsverteilungen auf die Summation (Integration) der Feldbeiträge infinitesimal kleiner Ladungsmengen geführt. Analog geht man beim Potential vor.
Wir betrachten eine Ladungsverteilung mit Gesamtladungsmenge Q. Eine kleineTeilladung Qi im Abstand ri zu unserem Aufpunkt r wird dann folgendes Potential erzeugen:
V i=
1 Qi
4  0 r i
Wir beziehen unser Potential dabei wieder auf .
Das Gesamtpotential am Ort r ist dann:
1 ∑i Q i
V r =∑i V i =
4  0
ri
Wir können das auch gleich in integraler Form für kontinuierliche Ladungsverteilungen formulieren (ri wird zu r'):
V r =
1
dQ
∫
4  0 r '
Hörsaal­Übung: Wir betrachten eine dünne, flache Kreisscheibe mit Radius R.
Sie trage die Ladung Q homogen über ihre Fläche verteilt. Wie groß ist das Potential
auf der Scheibenachse im Abstand x vom Zentrum der Scheibe?
dr
r
x
R
3.5 – Äquipotentiallinien und Äquipotentialflächen
Das elektrische Potential kann graphisch durch das Zeichnen von Äquipotentiallinien (in zwei Dimensionen) oder Äquipotentialflächen (in drei Dimensionen) dargestellt werden.
Eine Äquipotentialfläche oder ­linie ist die Menge aller Punkte für die das Potential den
gleichen Wert annimmt.
Die Verschiebung einer Testladung entlang einer Äquipotentiallinie oder auf einer Äquipotentialfläche führt demnach zu keiner Änderung der potentiellen Energie der Ladung. Daraus schlussfolgern wird:
Eine Äquipotentialfläche oder Äquipotentiallinien stehen stets senkrecht auf den
elektrischen Feldlinien.
Ist das elektrische Feldlinienbild gegeben, so kann die Äquipotentialfläche bzw. können die Äquipotentiallinien leicht gezeichnet werden.
Wir hatten gesehen, dass die elektrischen Feldlinien auf Metalloberflächen im elektrostatischen Fall senkrecht stehen. Wir halten also auch noch fest:
Die Oberfläche eines leitfähigen Objektes bildet im statischen Fall stets eine
Äquipotentialfläche.
3.6 – Potential eines elektrischen Dipols
Äquipotentiallinien für einen symmetrischen Dipol
Da elektrische Dipole in der Physik ( und auch in der Chemie ) eine recht große Rolle spielen, schauen wir uns auch noch das Potential eines Dipols an.
Wir betrachten dazu zwei Ladungen +Q und ­Q ( Q > 0 ) im Abstand l voneinander und suchen das Potential im Abstand r ( >>l ).
Wie üblich wählen wir V(r) = 0 und erhalten für den Aufpunkt das folgende Potential:
V=
r
r
­Q
r

Q
Q
1
−
r  r
4  0 r

=
r
Q
4  0 r r  r 
Dieser Ausdruck lässt sich vereinfachen für den (meist relevanten) Fall r >> l:
 r ≈ l cos und unter Vernachlässigung von  r im Nenner 1 Q l cos
V≈
4  0
r2

+Q
Erinnern wir uns an das Dipolmoment p = Ql, so folgt kompakter für das sogenannte Fernfeld des Dipols:
V=
⋅r
1 p
4  0 r 3
Im Vergleich zum Potential einer Punktladung fällt das Dipolpotential mit dem Abstand schneller ab, nämlich wie 1/r2. Wir hatten einen schnelleren Abfall auch schon für das elektrische Feld festgestellt.
Dipolmoment einiger Moleküle
Molekül
Dipolmoment ( C∙m )
pos. Teilladung bei
H2O
6.1∙10­30
H
HCl
3.4∙10­30
H
NH3
5.0∙10­30
H
Hörsaal­Übung: Wie groß ist die effektive Ladung am Kohlenstoff bzw. Sauerstoff
des CO­Moleküls? Wie groß ist das Potential auf der Dipolachse in der Nähe des
C­Atoms im Abstand 0.9 nm vom Zentrum des Dipols? Wie groß wäre dort das
Potential, wenn nur das Sauerstoff­Atom geladen wäre?
Der Abstand zwischen dem Kohlenstoff­ und Sauerstoffatom ist ca. 0.12 nm. Das
Dipolmoment beträgt ca. 8.0∙10­30 Cm.
3.7 – Bestimmung von E aus V
Die Invertierung der Linienintegration über das elektrische Feld zur Bestimmung des Potentials erlaubt es umgekehrt, das elektrische Feld aus dem Potential zu erhalten. Wie aber macht man das?
Wir schreiben zunächst in differentieller Form:
⋅d s =−E ds
dV =−E
s
dV ist die infinitesimale Potentialdifferenz entlang des Wegstücks ds.
Wir lösen nach Es auf:
E s =−
dV
ds
Demnach können wir fest halten:
Die Komponente des elektrischen Feldes längs einer gegebenen Richtung ist gleich
der negativen Änderungsrate des Potentials mit dem Abstand in dieser Richtung.
Man bezeichnet dV/ds als den Gradienten entlang der Richtung von ds.
Wenn die Richtung nicht vorgegeben ist, bezieht sich der Gradient auf die Richtung, in der die Ableitung den größten Wert erreicht.
E zeigt also immer in die Richtung in der sich das Potential am schnellsten mit dem Abstand ändert. Das ist natürlich keine große Überraschung, wenn wir uns an den Zusammenhang zwischen den elektrischen Feldlinien und den Äquipotentialflächen/linien erinnern. Diese standen immer senkrecht aufeinander. Die schnellste Änderung zeigt V aber natürlich entlang der senkrechten Richtung zwischen zwei Äquipotentialflächen/linien, also parallel zu den elektrischen Feldlinien.
Wenn E als Funktion der kartesischen Koordinaten x, y, z angegeben ist, so bedeutet dies allgemein:
 =E ,E ,E =−∂ V / ∂ x , ∂ V / ∂ y , ∂ V / ∂ z =−gradV =− ∇ V
E
x
y
z
Der Ausdruck
∂V
∂x
meint dabei die partielle Ableitung von V nach x (analog für y und z).
ist der sogenannte Nabla­Operator. Er hat in kartesischen Koordinaten die Form:
∇ ≡∂ / ∂ x , ∂ / ∂ y , ∂ / ∂ z 
Hörsaal­Übung: Bestimme das elektrische Feld an einem Punkt P auf der Achse
eines homogen geladenen Rings und einer homogen geladenen Scheibe.
3.8 – Elektrostatische potentielle Energie; das Elektronvolt
Bei der Bewegung einer Punktladung q zwischen zwei Punkten a und b mit den Potentialen Va und Vb ändert sich die elektrostatische potentielle Energie der Ladung um:
U =U b −U a =q V b − V a =qV ba
Gesetzt den Fall, wir haben mehrere Punktladungen. Was ist die elektrostatische potentielle Energie des Systems?
Üblicher­ und auch bequemerweise wählt man den Energienullpunkt so, dass die potentielle Energie verschwindet, wenn die Ladungen sehr weit voneinander entfernt sind. Demnach hat eine einzelne Punktladung Q1 keine potentielle Energie.
Bringen wir eine zweite Punktladung Q2 in die Nähe von Q1 so ist die potentielle Energie des Systems:
1 Q1Q2
U =Q 2 V =
4  0 r 12
Dies entspricht der Arbeit, die geleistet werden muss, um Q2 aus dem Unendlichen auf einen Abstand r12 an Q1 heranzubringen.
Nehmen wir noch eine dritte Ladung Q3 hinzu. Die zu leistende Arbeit ist
1 Q2Q3
1 Q1Q3
W=

4  0 r 23
4  0 r 13
Wir addieren dies zur schon vorhandenen potentiellen Energie und erhalten so für die potentielle Energie von drei Punktladungen:
1 Q1Q3
1 Q2Q3
1 Q1Q2
U=


4  0 r 13
4  0 r 23
4  0 r 12
Bei vier Ladungen sind es schon sechs Terme usw.
Diese Aufsummation wird in über Coulomb­Kräfte wechselwirkenden Vielteilchensystemen immer wieder vorkommen. Dabei muss man stets darauf achten, dass man nicht versehentlich Terme doppelt zählt.
Die typischen Energien von Elektronen und Atomen oder Molekülen sind nur ein winziger Bruchteil eines Joules. Deshalb wurde als deutliche “handlichere” Einheit für diesen Zweck das Elektronvolt ( eV ) eingeführt:
Ein Elektronvolt ( 1 eV ) entspricht dem Zuwachs an potentieller Energie, den eine
Elementarladung ( |e| ) beim Durchlaufen einer Spannungsdifferenz von 1 V erfährt.
Das bedeutet also:
1 eV =1.602⋅10−19 J
Hörsaal­Übung: Welche Arbeit ist nötig, um ein Wasserstoffatom zu “zerlegen”?
Wir nehmen dazu an, dass das Elektron und das Proton ursprünglich einen Abstand
von 0.529 Å haben (entspricht dem mittlerem Atomradius des Wasserstoffatoms
im Grundzustand).
3.9 – Kathodenstrahlröhre: TV, Monitor, Oszilloskop
Mit einer Kathodenstrahlröhre (CRT: cathode ray tube) lassen sich sehr elegant Spannungen und deren zeitlicher Verlauf visualisieren. Dazu werden CRTs in Oszilloskopen eingesetzt. Häufiger natürlich finden wir sie (noch!) in Fernsehgeräten und Computermonitoren.
(geheizt)
+++++
Kathode
­­­­­­­­
Ein wesentlicher Teil einer CRT ist der Strahlerzeuger. In ihm werden mittels des glühelektrischen Effekts Elektronen aus einer heißen Metalloberfläche ausgelöst. Der Effekt wurde von Thomas Edison (1847­1931) entdeckt während er mit Glühlampen experimentierte.
Anode
+
­
Spannungsquelle
Zwei metallische Platten (Elektroden) sind in einer evakuierten Glasröhre gegenüberliegend angeordnet. Eine Elektrode (Kathode) ist gegenüber der anderen Elektrode (Anode) negativ vorgespannt. Die Kathode wird geheizt, bis sie zu glühen beginnt. Man beobachtet dann einen Strom negativer Ladungen (Elektronen) von der Kathode zur Anode. Daher der Name “Kathodenstrahl”. Das Austreten der Elektronen kann in einer sehr groben Analogie mit dem Verdampfen von kochendem Wasser verglichen werden. Im Detail gibt es Unterschiede aufgrund der verschiedenen quantenmechanischen Natur von Elektronen und Wassermolekülen.
Zum Verständnis des Funktionsprinzips eines Oszilloskops ist es jetzt nur ein kleiner Schritt.
Zwischen Kathode und Anode wird noch ein Gitter eingebracht. Mit der Potentialeinstellung auf diesem Gitter lässt sich der Elektronenstrom variieren. Die Anode wird durchbohrt, so dass die Elektronen durch dieses Loch in den Halbraum dahinter austreten können. Sie gelangen nacheinander in das elektrische Feld zweier um 90° zueinander gedrehter Plattenkondensatoren (oder auch in ein Magnetfeld). Dort werden sie wahlweise in ±x­ oder ±y­Richtung abgelenkt. Sie treffen dann auf einen Schirm, den sie zur Fluoreszenz, d.h. zum Leuchten, anregen.
Oszilloskop mit Beschaltung
Triggerstufe
Schirm
Ablenkstufe