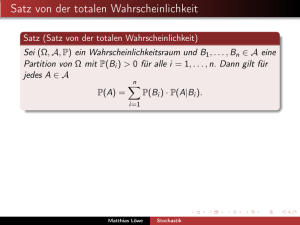
Ein alternativer Zugang zu bedingten Wahrscheinlichkeiten anhand

Ein alternativer Zugang zu bedingten
Wahrscheinlichkeiten anhand aktueller
Fehlvorstellungen:
Die Wahrscheinlichkeitsbegriffe als
Schlüssel zur Stochastik
Masterarbeit
vorgelegt dem Fachbereich 08 – Physik, Mathematik und Informatik
der Johannes Gutenberg-Universität Mainz
von
David Selzer (2682801)
Fach: Mathematik
Erstgutachter: Prof. Dr. Ysette Weiss-Pidstrygach
Zweitgutachter: Marcel Gruner
Inhaltsverzeichnis
1. Einleitung ..................................................................................................... 1
2. Sind Menschen gute Statistiker?................................................................ 5
3. Ein alternativer Zugang zur Stochastik .................................................. 16
3.1 Der Einstieg in die Stochastik – Die Wahrscheinlichkeitsbegriffe ..................... 16
3.2 Der Laplace-Wahrscheinlichkeitsbegriff .............................................................. 21
3.2.1 Arbeitsblatt I - Berechnung von Laplace-Wahrscheinlichkeiten ....................... 21
3.2.2 Arbeitsblatt II - Kombinatorischer Exkurs ......................................................... 26
3.2.3 Arbeitsblatt III - Kontinuierliche Ergebnismengen ............................................ 36
3.3 Der frequentistische Wahrscheinlichkeitsbegriff ................................................. 39
3.3.1 Arbeitsblatt I - Das empirische Gesetz der großen Zahlen ................................ 39
3.3.2 Arbeitsblatt II - Der Begriff der Unabhängigkeit............................................... 47
3.3.3 Arbeitsblatt III - Wahrscheinlichkeitsverteilungen ............................................ 51
3.4 Der subjektive Wahrscheinlichkeitsbegriff .......................................................... 57
3.4.1 Arbeitsblatt I - Die bedingte Wahrscheinlichkeit ............................................... 57
3.4.2 Arbeitsblatt II - Die Basisrate ............................................................................ 65
3.5 Der axiomatische Wahrscheinlichkeitsbegriff ...................................................... 69
3.5.1 Arbeitsblatt I - Die Axiomatik nach Kolmogorov............................................... 69
3.5.2 Arbeitsblatt II - Zufallsvariablen & Erwartungswert/ Varianz .......................... 75
3.5.3 Arbeitsblatt III - Das schwache Gesetz der großen Zahlen ............................... 80
4. Die stochastische Modellbildung .............................................................. 85
5. Fazit ............................................................................................................ 90
6. Anhang ....................................................................................................... 96
6.1 Arbeitsblätter ........................................................................................................... 96
6.2 Tabelle – Möglichkeiten und Grenzen der Wahrscheinlichkeitsbegriffe ........ 139
6.3 Lösungen zu Beweisen .......................................................................................... 142
I
6.4 Verwendete Abbildungen auf den Arbeitsblättern ............................................ 143
6.5 Lehrplan Mathematik ........................................................................................... 145
7. Quellen und Literaturverzeichnis .......................................................... 148
II
Abbildungsverzeichnis
Abbildung 1:Wahrscheinlichkeiten und natürliche Häufigkeiten. ...................................... 12
Abbildung 2: Würfelmöglichkeiten. ................................................................................... 23
Abbildung 3: Baumdiagramm Zählfigur I. ......................................................................... 28
Abbildung 4: Baumdiagramm Zählfigur II. ........................................................................ 28
Abbildung 5: Baumdiagramm Zählfigur III. ....................................................................... 29
Abbildung 6: Baumdiagramm Teilungsproblem (kombinatorisch). ................................... 34
Abbildung 7: Baumdiagramm Teilungsproblem (verkürzt)................................................ 34
Abbildung 8: Empirisches Gesetz der großen Zahlen. ........................................................ 44
Abbildung 9: ε-Schlauch. .................................................................................................... 45
Abbildung 10: Baum für den vierfachen Münzwurf und das Pascal‘sche Dreieck. ........... 53
Abbildung 11: Formen der Binomialverteilung. ................................................................. 55
Abbildung 12: Baumdiagram HIV-Erkrankung (absolute Häufigkeiten). .......................... 63
Abbildung 13: Baumdiagramm HIV-Erkrankung (relative Häufigkeiten). ........................ 63
Abbildung 14: Basisrate. ..................................................................................................... 66
Abbildung 15: Lösung quadratische Funktion. ................................................................... 73
Abbildung 16: Chuck a Luck. ............................................................................................. 78
Abbildung 17: Stochastische Modellbildung. ..................................................................... 85
Abbildung 18: Lösung Sehnenproblem I. ........................................................................... 87
Abbildung 19: Lösung Sehnenproblem II. .......................................................................... 87
Abbildung 20: Lösung Sehnenproblem III. ......................................................................... 87
III
Tabellenverzeichnis
Tabelle 1: Lehrplan Mathematik. .......................................................................................... 1
Tabelle 2: Schätzungen Quaderwürfel. ............................................................................... 18
Tabelle 3:
1
√𝑛
– Gesetz. ........................................................................................................ 46
Tabelle 4: Wahrscheinlichkeitsverteilung Bino-Ley. .......................................................... 53
Tabelle 5: Wahrscheinlichkeitsverteilungen Würfel und Quader. ...................................... 58
Tabelle 6: Vierfeldertafel HIV-Erkrankungen. ................................................................... 62
Tabelle 7: Wahrscheinlichkeitsverteilungen für Würfelverteilungen I. .............................. 75
Tabelle 8: Wahrscheinlichkeitsverteilungen für Würfelverteilungen II. ............................ 75
Tabelle 9: Wahrscheinlichkeitsverteilungen für Würfelverteilungen III. ........................... 75
Tabelle 10: Vergleich Datenanalyse und Wahrscheinlichkeitsrechnung. ........................... 76
Tabelle 11: Chuck a Luck. .................................................................................................. 78
Tabelle 12: Vergleich empirisches und schwaches Gesetz der großen Zahlen. .................. 82
Tabelle 13: Eigener Lehrplan. ............................................................................................. 92
IV
1. Einleitung
„Zentrales Anliegen dieses Themenbereichs [Stochastik] ist es, die Schülerinnen und Schüler 1 mit
Denkweisen und Verfahren der Stochastik vertraut zu machen. Dabei steht auch im Leistungskurs der
Anwendungsbezug und nicht der Aufbau einer mathematischen Theorie im Mittelpunkt.
Aufbauend auf den BS [Bildungsstandards] der Sek I wird der Wahrscheinlichkeitsbegriff vertieft und
ein Schwerpunkt auf Wahrscheinlichkeitsverteilungen von Zufallsgrößen gelegt. Dabei beschränkt sich
der Lehrgang auf diskrete Zufallsgrößen; im Mittelpunkt steht die Binomialverteilung. […]“2
Tabelle 1: Lehrplan Mathematik.
Ziele/ Inhalte (Sach- und Methodenkompetenz)
2. Wahrscheinlichkeiten bestimmen und in Sachzusammenhangen
interpretieren
[…]
5. Die Begriffe „bedingte Wahrscheinlichkeit „und „Unabhängigkeit zweier Ereignisse”kennen
und anwenden
6. Die Begriffe „Zufallsgröße“ und
„Wahrscheinlichkeitsverteilung“
kennen und an Beispielen erläutern
7. Die Begriffe „Erwartungswert“,
„Varianz“ und “Standardabweichung“ einer diskreten Zufallsgröße kennen und anwenden
[…]
12. Verstehen, wie man Wahrscheinlichkeiten einer binomialverteilten Zufallsgröße annäherungsweise mit Hilfe der Gaußschen Integralfunktion Φ (Standard-Normalverteilung) bestimmt
Hinweise zur Unterrichtsgestaltung
und Methodenkompetenz
Der Schwerpunkt liegt auf der Entwicklung eines inhaltlichen
Verständnisses des Wahrscheinlichkeitsbegriffs. Die Stabilisierung der relativen Häufigkeit soll an Beispielen erfahren werden (empirisches Gesetz der großen Zahlen); die LaplaceWahrscheinlichkeit wird als Spezialfall behandelt. Zur Bestimmung von Wahrscheinlichkeiten können systematische Abzählverfahren verwendet werden; eine ausführliche Behandlung kombinatorischer Regeln ist nicht intendiert.
[…]
Im Rahmen des pädagogischen Freiraums sollte in diesem Zusammenhang auch der Satz von Bayes behandelt werden.
Bei der Anwendung in Sachaufgaben kommt es vor allem darauf an, dass die Schüler verstehen, welche Folgerungen man
aus den Kennwerten für das Sachproblem ziehen kann. Hier
bietet es sich an, exemplarisch eine statistische Erhebung zu
planen und zu beurteilen.
[…]
Die Möglichkeit der Approximation soll anschaulich, z. B. anhand von Histogrammen, einsichtig gemacht werden. Hierfür
empfiehlt sich der Einsatz eines geeigneten Computerprogramms. Die Bestimmung der Näherungswerte erfolgt mit
Hilfe von Tabellen oder Rechnern. Im Rahmen des pädagogischen Freiraums können darauf aufbauend die Normalverteilung definiert und Anwendungsbeispiele behandelt werden.“
Quelle: Mathea: Lehrplan Mathematik, S. 53f.
Auf den ersten Blick klingen diese Forderungen des Lehrplans für die gymnasiale Oberstufe
schlüssig und spiegeln durch die Betonung des Anwendungsbezugs und die Reduzierung
des mathematischen Kalküls das kompetenzorientierte Lernen wider. Allerdings tauchen im
zweiten Teil der Forderungen (vgl. oberhalb der Tabelle 1) insbesondere bei der Vorbereitung des Unterrichts Unklarheiten auf, da aufbauend auf der Sek. I „der Wahrscheinlichkeitsbegriff“ vertieft werden soll. Durch die sinnvolle Verbindung mit der Sek. I, in der
1
Aus Gründen der besseren Lesbarkeit wird auf die gleichzeitige Verwendung männlicher und weiblicher
Sprachformen verzichtet. Sämtliche Personenbezeichnungen gelten gleichwohl für beiderlei Geschlecht.
2
Der vollständige Lehrplan für den Leistungskurs ist im Anhang zu finden. Vgl. Mathea: Lehrplan Mathematik, S. 53f.
1
hauptsächlich die beschreibende Statistik behandelt wird, zeichnet sich ab, dass hier der frequentistische Wahrscheinlichkeitsbegriff gemeint ist. Dies wird auch durch die angegebenen
Ziele/ Inhalte des Lehrplans deutlich (vgl. Tabelle 1). Im zweiten Unterpunkt, der die Bestimmung von Wahrscheinlichkeiten thematisiert, wird gefordert, dass „die Stabilisierung
der relativen Häufigkeit an Beispielen erfahren werden (empirisches Gesetz der großen Zahlen) [soll]; die Laplace-Wahrscheinlichkeit wird als Spezialfall behandelt.“3 An dieser Stelle
taucht mit der Laplace-Wahrscheinlichkeit ein zweiter Wahrscheinlichkeitsbegriff auf, der
lediglich als Spezialfall des frequentistischen behandelt werden soll. Trotz der sinnvollen
Betonung des Datenbezugs ist dies problematisch, da die Laplace-Wahrscheinlichkeit eine
theoretische Bestimmung der Wahrscheinlichkeit im Vorhinein (a priori) darstellt. Im frequentistischen Wahrscheinlichkeitsmodell werden hingegen Wahrscheinlichkeiten im Nachhinein (a posteriori) mit Hilfe des empirischen Gesetzes der großen Zahlen berechnet.
Der Lehrplan beinhaltet des Weiteren die Forderung, den Schwerpunkt auf die Wahrscheinlichkeitsverteilungen der Zufallsgrößen4 zu legen. Dabei soll sich auf diskrete Wahrscheinlichkeitsverteilungen (insbesondere die Binomialverteilung) beschränkt werden. Dem Gedankengang des Lehrplans folgend, sollen aus empirischen Wahrscheinlichkeitsverteilungen
durch die Anwendung des empirischen Gesetzes der großen Zahlen theoretische Wahrscheinlichkeitsverteilungen entdeckt werden. Dies wird durch den nächsten Punkt (7.) verdeutlicht, indem die Begriffe Erwartungswert, Varianz und Standardabweichung mit Hilfe
einer statistischen Erhebung interpretiert werden sollen. Diese Interpretation ist ebenfalls
durch das empirische Gesetz der großen Zahlen möglich. Es ist nicht ersichtlich, warum
dafür eine Zufallsvariable eingeführt werden muss. Mit der Vorgehensweise des Lehrplans
reichen die bisherigen Wahrscheinlichkeitsbegriffe (frequentistischer und Laplace) vollkommen aus. Somit könnte auf die Axiomatik Kolmogorovs, zu der die Zufallsvariable gehört, verzichtet werden. Es hat aber durchaus einen Sinn die Zufallsvariable einzuführen, da
nicht alle Probleme mit Hilfe der inhaltlichen Wahrscheinlichkeitsbegriffe gelöst werden
können. Insbesondere betrifft dies das Konvergenzverhalten des empirischen Gesetzes der
großen Zahlen (lediglich eine stochastische und keine analytische Konvergenz) und die kontinuierlichen Wahrscheinlichkeitsräume. Beide Schwierigkeiten werden vom Lehrplan nicht
erwähnt, sodass die Einführung der Zufallsvariable für die Schüler nicht verständlich werden
kann.
3
4
Ebd. S. 53.
Im Folgenden mit Zufallsvariablen bezeichnet.
2
Außerdem führt dieser Zustand in vielen Schulbüchern zu dem Problem, dass sie bei diesen
Themen oft ungenau und unsauber arbeiten. Die Schwankungen der relativen Häufigkeit
sind unerwünscht und werden daher von den Schulbüchern entweder komplett ignoriert oder
durch das starke Gesetz der großen Zahlen verborgen. Das Thema der kontinuierlichen Mengen wird gemäß des Lehrplans komplett reduziert, obwohl es bereits im Bereich des LaplaceWahrscheinlichkeitsmodells zu unlösbaren Schwierigkeiten führt. So können im kontinuierlichen Wahrscheinlichkeitsraum keine Laplace-Wahrscheinlichkeiten bestimmt werden.5
Diese Problematik wird im Bereich der Normalverteilung besonders deutlich und stellt
grundsätzlich einen Widerspruch zum Bruner´schen Spiralprinzip dar. Laut Lehrplan soll
die Binomialverteilung durch die Normalverteilung approximiert werden. Hinter der Approximation steckt erneut die unsichere stochastische Konvergenz des empirischen Gesetzes der
großen Zahlen. Darüber hinaus wird der diskrete Wahrscheinlichkeitsraum endgültig verlassen. Die Bestimmung von Wahrscheinlichkeiten über das Integral der Dichtefunktion (also
über eine Fläche) kann ohne die Behandlung von kontinuierlichen Wahrscheinlichkeitsräumen nicht verstanden werden. Somit kann die geforderte Beschränkung auf diskrete Zufallsvariablen im Unterrichtsverlauf nicht durchgesetzt werden.
Außerdem fehlt mit dem subjektiven Wahrscheinlichkeitsbegriff eine weitere Möglichkeit,
Wahrscheinlichkeiten zu bestimmen. Hierbei wird von der Intuition der Schüler ausgegangen und erfasst, wie „Lernen aus der Erfahrung“, mathematisch vonstattengehen kann.
Grundlage dafür ist die bedingte Wahrscheinlichkeit und der Satz von Bayes. Obwohl diese
Thematik ebenfalls im Lehrplan unter Punkt fünf erwähnt wird, wirkt sie dennoch wie ein
Fremdkörper im vorgeschlagenen Ablauf. Die Fokussierung auf den frequentistischen
Wahrscheinlichkeitsbegriff und dessen notwendige Unabhängigkeitsannahme schließt die
bedingten Wahrscheinlichkeiten förmlich aus.
Prinzipiell gibt es zwei Wege diese Schwierigkeiten im Umgang mit dem Lehrplan zu lösen:
Es könnte die Axiomatik Kolmogorovs an den Anfang gestellt und anhand dieser die mathematische Theorie entwickelt werden. Dies ist grundsätzlich sinnvoll, denn so eine Vorgehensweise ist für die Mathematik grundlegend und stellt eine ihrer Stärken dar. Allerdings
steht dabei die Struktur der Mathematik und nicht die Lernenden selbst im Vordergrund.
5
Boor: Lambacher Schweizer, S. 36.
Lergenmüller: Mathematik Neue Wege, S. 29.
Griesel: Elemente der Mathematik, S. 16.
3
Daher ist dieser rein axiomatische Aufbau für die Schule abzulehnen. Vielmehr soll ein genetisches Prinzip als Ausgangspunkt gesetzt und Anwendungssituationen ins Zentrum gerückt werden.6 Dabei sollte mit der Intuition der Schüler begonnen werden, denn
„was ein Punkt, ein rechter Winkel, ein Kreis ist, weiß ich schon vor der ersten Geometriestunde, ich
kann es nur noch nicht präzisieren. Ebenso weiß ich schon, was Wahrscheinlichkeit ist, ehe ich es definiert habe.“7
Diese Vorstellung über die Stochastik beschreibt Hans Freudenthal in seinem Werk „Wahrscheinlichkeit und Statistik“ und bildet die Grundlage dieser Arbeit. Daher wird im zweiten
Kapitel die von Freudenthal aufgeworfene Frage beantwortet, ob Menschen gute intuitive
Statistiker sind. Dabei wird sich vor allem auf die psychologischen Forschungen nach
Kahneman/ Tversky und Gigerenzer gestützt.8 Allerdings werden die Probleme des Lehrplans durch einen stärkeren Einbezug der Intuition nicht gelöst, denn auch dieser hat den
Anspruch, von Anwendungen auszugehen. Daher soll ein alternativer Zugang zur Stochastik
vorgestellt werden, der die Chancen und Grenzen der einzelnen Wahrscheinlichkeitsbegriffe
(Laplace-, frequentistisch, subjektiv und axiomatisch) ins Zentrum rückt.
Dazu wurden Arbeitsblätter9 entwickelt, die jeweils drei Aufgaben und gegebenenfalls eine
Vertiefung zu einer Thematik umfassen. Nach einem Einstiegsbeispiel, das die inhaltlichem
Wahrscheinlichkeitsbegriffe aufwirft, wird sich den Chancen und Grenzen des Laplace-, des
frequentistischen und des subjektiven Wahrscheinlichkeitsbegriffs zugewandt. Ein besonderes Augenmerk liegt dabei auf den angesprochenen Schwierigkeiten der stochastischen Konvergenz, der kontinuierlichen Wahrscheinlichkeitsräume und dem „Schattendasein“ der bedingten Wahrscheinlichkeiten. Die Schüler erkennen, dass die Probleme der kontinuierlichen Wahrscheinlichkeitsräume und der stochastischen Konvergenz mit den inhaltlichen
Wahrscheinlichkeitsbegriffen nicht gelöst werden können. Daher der axiomatische Wahrscheinlichkeitsbegriff eingeführt. Dabei wurde darauf geachtet, dass die allgemeinen Kompetenzen (Mathematisch argumentieren; Probleme mathematisch lösen; Mathematisch modellieren; Mathematische Darstellungen verwenden; Mit Mathematik symbolisch/ formal/
technisch umgehen; Mathematisch kommunizieren) beachtet wurden. Eine besondere Position nimmt dabei die Kompetenz „Mathematisch modellieren“ ein, da die Wahrscheinlichkeitsbegriffe entsprechende Modelle mit sich bringen, die fortwährend reflektiert werden
6
Büchter; Henn: Elementare Stochastik, S. 4.
Freudenthal: Wahrscheinlichkeit und Statistik, S.7.
8
Zum Einstieg in die Thematik behandeln die Schüler einige Aufgaben aus der psychologischen Forschung.
Diese können den Wahrscheinlichkeitsbegriffen zuordnet werden und daher an passender Stelle erneut aufgegriffen werden. Die Aufgaben sollen zur Reflexion ihrer eigenen statistischen Sachkenntnis anregen und zur
Motivation der verschiedenen Wahrscheinlichkeitsmodelle beitragen.
9
Die ausgearbeiteten Arbeitsblätter befinden sich im Anhang.
7
4
müssen. Durch diese Reflexion wird den Schülern bewusst, dass die Mathematik - insbesondere die Stochastik - nicht die Realität abbilden kann, sondern nur in Modellen arbeitet, die
mit Unsicherheit belastet sind. Auf dem letzten Arbeitsblatt finden sich daher Aufgaben zur
stochastischen Modellbildung.
Bei der Konzeption der Arbeitsblätter wurde auf vorhandene stochastische Lehrwerke, wie
„Büchter; Henn: Elementare Stochastik“, „Eichler; Vogel: Leitidee Daten und Zufall“ und
für den subjektive Wahrscheinlichkeitsbegriff „Wassner; Biehler: Förderung Bayesianischen Denkens“ zurückgegriffen. Zum Vertiefen der einzelnen thematischen Aspekte werden daher diese Werke und das Schulbuch „Neue Wege“ empfohlen. 10 Die Umstrukturierung des vorgeschlagenen Unterrichtsablaufs durch die Analyse der Wahrscheinlichkeitsbegriffe ist allerdings neu. Ziel der Arbeit ist es, dass die Schüler im Mathematikunterricht zu
mündigen Bürgern erzogen werden, die „Kompetenzen für den kritischen Umgang mit Daten, Chancen und Risiken“11 erlernt haben.
2. Sind Menschen gute Statistiker?
„The theory of probabilities is at bottom nothing but common sense reduced to calculus; it enables us
to appreciate with exactness that which accurate minds feel with a sort of instinct for which ofttimes
they are unable to account."12
So äußerte sich Pierre-Simon de Laplace 1814 in seinem Werk „A philosophical essay on
probabilities“ über die Stochastik. Für ihn und weitere bedeutende Mathematiker wie
Condorcet und Poissoin spiegelt die Mathematik, insbesondere die Stochastik, den gesunden
Menschenverstand wider. Dies ist aus zweierlei Gründen nicht verwunderlich: Zum einen
war die Zeit der Aufklärung durch die historischen Ereignisse von einem großen Fortschrittsoptimismus geprägt. Zum anderen brachte insbesondere der Laplace-Wahrscheinlichkeitsbegriff, der in dieser Zeit hauptsächlich verwendet wurde, die notwendige Sicherheit, um
das theoretische Kalkül mit den Anwendungen gleichzusetzen. Die Unterscheidung zwischen einem objektiven und einem subjektiven Wahrscheinlichkeitsbegriff war nicht notwendig.13
Dies bedeutet nicht, dass die Mathematiker zu dieser Zeit nicht über unterschiedliche Ergebnisse diskutierten oder sich zum Teil auch irrten. Die Diskussionen in den Briefwechseln
10
Auf eine Ausrichtung der Arbeitsblätter im Sinne einer Unterrichtsverlaufsplanung wurde daher großenteils
verzichtet.
11
Biehler: Daten und Zufall, S. 5.
12
Laplace: Philosophical essay, S. 196.
13
Wassner; Biehler: Förderung Bayesianischen Denkens, S.15.
5
zwischen Pierre de Fermat und Blaise Pascal aus dem Jahr 1654 werden heute von Historikern als die Geburtsstunde der Wahrscheinlichkeitstheorie angesehen.14 Ein Problem, über
das sich die beiden Mathematiker miteinander austauschten, war die sogenannte „Wette des
Chevalier de Méré“:
„Der Chevalier de Méré war ein leidenschaftlicher Spieler und lebte im Frankreich des 17. Jahrhunderts.
Eines der Spiele, mit denen er seine Mitspieler verführte, war das folgende: ‚Wir werfen einen Würfel
viermal. Wenn dabei eine oder mehrere Sechsen sind, gewinne ich. Wenn keine Sechs dabei ist, gewinnen Sie.‘ Soweit wir wissen, waren seine Würfel fair; dennoch gewann der Chevalier mit diesem Spiel
regelmäßig Geld. Schließlich fand er keine Opfer mehr, oder das Spiel wurde auf die Dauer eintönig was immer der Grund war, er dachte sich eine Variante aus, die ebenso lukrativ sein sollte. Hier ist das
neue Spiel, das der Chevalier seinen Mitspielern anbot: Doppel-Sechs: Wir werfen ein Paar von Würfeln
24 Mal. Wenn dabei eine Doppel-Sechs oder mehrere sind, gewinne ich. Wenn keine Doppel-Sechs
dabei ist, gewinnen Sie.“15
De Mérés Überlegungen sind offensichtlich: Da er auf mindestens eine 6 in vier Würfen
wettete und die Doppel-6 sechsmal seltener als die einfache 6 fällt, erhöhte er die Wurfanzahl
auf 24 (= 4∙6). Somit dachte der Chevalier, dass er auch bei dieser Wette Gewinne erzielen
wird. Allerdings bestätigte sich die Annahme de Mérés nicht, da er nach einiger Zeit bemerkte, dass er häufiger verlor als gewann. Somit wandte er sich an die beiden bedeutendsten
Mathematiker dieser Zeit: Fermat und Pascal. Deren Antwort auf das Problem des Chevaliers würde in der heutigen Notation folgendermaßen aussehen:
1
Mit Hilfe des Laplace-Wahrscheinlichkeitsbegriffs kann eine Wahrscheinlichkeit von für eine 6 und
damit die Wahrscheinlichkeit von
5
6
6
für keine 6 angenommen werden. In der ersten Wettmodifikation
5
5
5
5
verliert der Chevalier mit einer Wahrscheinlichkeit von P(keine 6 in vier Würfen) = ∙ ∙ ∙ = 0,482.
6 6 6 6
De Méré gewann also in 51,8%, also in etwas mehr als der Hälfte der Spiele. In der modifizierten Wette
nahm der Chevalier richtigerweise an, dass die Doppel-6 sechsmal seltener als die 6 fällt, also mit einer
1
35
Wahrscheinlichkeit von . Die Wahrscheinlichkeit für keine Doppel-6 beträgt damit: . Wir können
36
36
5
die Wahrscheinlichkeit für keine Doppelsechs in 24 Würfen berechnen. Diese beträgt ( )24 = 0,509.16
6
De Méré verlor daher in etwas mehr als der Hälfte der Spiele. Es war also keineswegs das
Pech des Chevaliers, das zu seinen Verlusten beitrug, sondern wahrscheinlichkeitstheoretische Überlegungen.
In diesem Beispiel werden sich die drei inhaltlichen Wahrscheinlichkeitsbegriffe deutlich:
Der subjektive Wahrscheinlichkeitsbegriff wird durch die Intuition des Chevaliers, der frequentistische Wahrscheinlichkeitsbegriff durch die langen Versuchsreihen und der LaplaceWahrscheinlichkeitsbegriff durch die theoretischen Überlegungen für die Würfelwahrscheinlichkeiten repräsentiert. Insbesondere der Widerspruch zwischen dem subjektiven und
14
Winter: Zur intuitiven Aufklärung, S. 27.
Gigerenzer: Die Evolution, S. 4.
16
Ebd. S. 2.
Krämer: Denkste, S. 107.
15
6
dem objektiven Wahrscheinlichkeitsbegriff faszinierte Pascal und Fermat und sie formulierten in ihren weiteren Überlegungen die Gesetze, die später Kolmogorov zu seinen Axiomen
machte: die Nichtnegativität, die Normiertheit (die Wahrscheinlichkeiten für Elementarereignisse ergeben zusammen 1) und die Additivität (die Wahrscheinlichkeit für zwei disjunkte Ereignisse ist die Summe der Wahrscheinlichkeiten der beiden Ereignisse). 17 Auch
Pascal und Fermat waren wie Laplace Deterministen. Sie wollten mit Hilfe der klassischen
Theorie (Laplace-Wahrscheinlichkeitsbegriff) eine absolute Gewissheit erlangen. Unsicherheit gab es für sie nicht, diese war nur der Unkenntnis der Nicht-Mathematiker zuzuschreiben.18 Pascals Charakterisierung von de Méré in den erwähnten Briefen spiegelt dieses Denken wider:
„Ich habe nicht die Zeit, Ihnen eine Schwierigkeit zu erläutern, die M... [de Méré] sehr befremdete,
denn er ist ein sehr tüchtiger Kopf, aber er ist kein Mathematiker (das ist, wie Sie wissen, ein großer
Mangel), und er begreift nicht einmal, daß eine mathematische Linie bis ins Unendliche reicht, und ist
zutiefst davon überzeugt, daß sie sich aus einer endlichen Zahl von Punkten zusammensetzt; ich habe
ihn niemals davon abbringen können. Wenn Sie das zustande brächten, würden Sie ihn vollkommen
machen.“19
Im Laufe des 19. Jahrhunderts verstärkte sich diese Auffassung durch die zunehmende
Menge an Daten, die durch die Mathematik beschrieben wurde. Dadurch wurden die Intuition und die Vermutung unbedeutender. Es ging vielmehr um die Beschreibung der Natur
durch Tatsachen bzw. Wahrheiten. Dies bedeutet nicht zwangsläufig, dass die Intuition
grundsätzlich im Widerspruch zur Theorie stehen musste. Bernoulli schrieb über sein schwaches Gesetz der großen Zahlen an Leibniz, dass dieses „auch der dümmste Mensch mittels
eines naturgegebenen Instinkts von allein und ohne vorherige Instruktion“20 verstehen
würde. Die Unterscheidung zwischen objektiven und subjektiven Wahrscheinlichkeitsbegriff rückte die Fragestellung in den Fokus, ob die menschliche Intuition dem wahrscheinlichkeitstheoretischen Kalkül entspricht.21
Antworten auf diese Fragen versucht die psychologische Forschung seit Mitte des 20. Jahrhunderts zu erzielen. Die ersten Forschungen dieser Jahre (insbesondere Philip und
Edwards) beschrieben das menschliche Gehirn als intuitiven Statistiker.22 Diesen Ergebnissen widersprachen insbesondere Kahneman und Tversky in den 1970er Jahre.23 An dieser
17
Büchter; Henn: Elementare Stochastik, S. 183.
Steinbring: Entwicklung des Wahrscheinlichkeitsbegriffs, S. 23.
19
Wirths: Geburt der Stochastik, S.4.
20
Wassner; Biehler: Förderung Bayesianischen Denkens, S. 13.
21
Krauss: Wahrscheinlichkeit und Intuition, S. 139.
22
Wassner; Biehler: Förderung Bayesianischen Denkens, S. 14.
Gigerenzer: Repräsentation von Information, S. 108.
23
Eine Zusammenfassung der Ergebnisse liefert: Kahneman: Schnelles Denken.
18
7
Stelle sollen drei bekannte Probleme aus den Forschungen Kahneman und Tverskys thematisiert werden, die zeigen, dass Menschen tendenziell keine guten Statistiker sind:
„150 Jahre nach Laplace hatte sich die positive Bewertung der Eingangsfrage ins Gegenteil verkehrt.
Heuristiken dienten in der Folge als theoretische Erklärung für eine Fülle von identifizierten systematischen Diskrepanzen („fallacies“) zwischen der Urteilsbildung und der Wahrscheinlichkeitstheorie.“24
Als erstes Beispiel werden drei mögliche Folgen für einen fünffachen Münzwurf betrachtet:
Welche der Folgen ist am wahrscheinlichsten?
A: Kopf – Kopf – Kopf – Zahl – Zahl – Zahl
B: Zahl – Zahl – Zahl – Zahl – Zahl – Zahl
C: Kopf – Zahl – Kopf – Kopf – Zahl – Kopf
Im Hinblick auf die Intuition wird davon ausgegangen, dass diese Folgen nicht gleichwahrscheinlich sein können. Dies ist aber falsch. Alle drei Folgen sind gleichwahrscheinlich, weil
die Ereignisse als unabhängig voneinander sowie Kopf und Zahl als gleichwahrscheinlich
angenommen werden können.25 Folge C wird aber als viel wahrscheinlicher angesehen, weil
das menschliche Gehirn ständig nach Mustern sucht. Durch diesen Fehlschluss verloren
schon viele Glücksspieler Geld. Fällt beispielsweise beim Roulette eine lange Serie von roten Zahlen, ist man versucht beim nächsten Wurf auf Schwarz zu setzen. Auf Grund der
Unabhängigkeit der Ergebnisse ist es allerdings egal, welche Farben davor gefallen sind.26
Der nächste Wurf hat sowohl für die Farbe Rot als auch für Schwarz die (Laplace-) Wahr1
scheinlichkeit 2. Als Begründung für die falsche Intuition wird die Stabilisation der relativen
Häufigkeit um die „objektive Wahrscheinlichkeit“ gemäß des empirischen Gesetzes der großen Zahlen angegeben.27 Allerdings stabilisiert sich nur die relative Häufigkeit und nicht die
absolute Häufigkeit. Hinter dieser Fehlvorstellung steht die Meinung, dass bei etwa 1.000
Würfen circa 500-mal Kopf bzw. Rot fallen muss. Daher werden oft Zahlen getippt, die
bisher selten erschienen sind. Allerdings werden die absoluten Häufigkeiten jede feste
Schranke mit laufender Versuchszahl überschreiten.28 Das Gesetz der großen Zahlen arbeitet
nicht wie ein Buchhalter, sondern eher durch „Überschwemmung“. Abweichungen in den
absoluten Häufigkeiten werden sozusagen durch die sehr großen Nenner in den relativen
Häufigkeiten beglichen.29
24
Wassner; Biehler: Förderung Bayesianischen Denkens, S. 15.
Strick: Vorstellungen, S. 52
26
Die hohe Bedeutung der Unabhängigkeitsannahme für die Stochastik wird durch zwei Trugschlüsse vertieft.
Ohne den formalen Aspekt der bedingten Wahrscheinlichkeit können so die inhaltlichen Aspekte dieser angesprochen werden.
27
Krämer: Denkste, S. 40.
28
Büchter; Henn: Elementare Stochastik, S. 176.
Kilian: Fundierung des Begriffs, S. 15.
29
Barth; Haller: Stochastik Leistungskurs, S. 251.
25
8
Das empirische Gesetz der großen Zahlen spielt auch im nächsten, leicht abgewandelten
Problem von Kahneman und Tversky eine große Rolle:
Was halten Sie für wahrscheinlicher?
(1)Mindestens 7 von 10 Neugeborenen in einem Krankenhaus sind Mädchen.
(2)Mindestens 70 von 100 Neugeborenen in einem Krankenhaus sind Mädchen.
Es gab drei Antwortmöglichkeiten:
A. (1) ist wahrscheinlicher,
B. (2) ist wahrscheinlicher,
C. (1) und (2) sind gleichwahrscheinlich. 30
Nach dem empirischen Gesetz der großen Zahlen ist eine solche Abweichung von der erwarteten Mädchengeburtsrate31 nur bei kleinen Stichproben (in diesem Fall in dem Krankenhaus mit der kleineren Geburtenanzahl) zu erwarten. Damit ist A die einzig sinnvolle
Antwort. In vielen Studien, die diese Version der Frage stellten, wurde allerdings ein anderes
Ergebnis gefunden. Exemplarisch dafür steht die Befragung von 153 Mathematikstudierenden, unter denen 14% für A, 16% für B und 70% für C stimmten.32
Zwar kann das empirische Gesetz der großen Zahlen von vielen Personen wiedergegeben
werden, allerdings wurde es nicht wirklich verstanden. Viele Personen unterschätzen die
Bedeutung des Stichprobenumfangs. Für das menschliche Gehirn zählt alleine der Stichprobenanteil. Dies wird besonders darin deutlich, dass der Nenner oftmals komplett vernachlässigt wird und der Zähler alleine für Entscheidungen ausschlaggebend ist.33
Das wohl bekannteste Problem Kahneman und Tverkys ist das sogenannte Taxi-Problem:
Ein Taxi war an einem nächtlichen Verkehrsunfall mit Fahrerflucht beteiligt. In der Stadt, in der der
Unfall passierte, gibt es zwei Taxiunternehmen: Eines mit grünen und eines mit blauen Taxis. Folgende
Daten sind gegeben: (i) 85% aller Taxis in der Stadt sind blau, die anderen 15% sind grün. (ii) Ein Zeuge
identifizierte das davonfahrende Taxi als „grün“. Das Gericht untersuchte nun die Fähigkeit des Zeugen,
die Farbe eines Taxis bei Nacht richtig zu identifizieren. In der Versuchsreihe (die Hälfte der Taxis war
blau, die andere Hälfte war grün), konnte der Zeuge beide Farben zu 80% korrekt identifizieren, aber
zu 20% irrte er. Wie groß ist die Wahrscheinlichkeit, dass das Unfalltaxi wirklich grün und nicht blau
war?34
Nach dem Satz von Bayes wäre circa 41% die richtige Antwort gewesen. Die Probanden
schätzten die Wahrscheinlichkeit allerdings auf circa 80%. Kahneman und Tversky erklärten
dies durch die sogenannte Basisratenvernachlässigung („base-rate-neglect“). In der Folge
wurde vor allem diese Heuristik vielfach untersucht. Dabei fungierte das Taxiproblem lediglich als Beispiel.35 Im Schulalltag haben sich, insbesondere bei der Behandlung des Satzes von Bayes, medizinisch-diagnostische Aufgaben etabliert:
30
Büchter; Henn: Elementare Stochastik, S. 176.
Es wird eine Wahrscheinlichkeit von circa 50% für eine Mädchengeburt angenommen.
32
Büchter; Henn: Elementare Stochastik, S. 176.
Sedlmeier: Statistik ohne Formeln, S. 86.
33
Sedlmeier: Wie kann Intuition, S. 230.
34
Kahneman; Tversky: On the Psychology, S. 241.
35
Daher wird auf dem Intuitionsarbeitsblatt neben dem Taxiproblem auch eine Gerichtsverhandlung mit dem
gleichen mathematischen Hintergrund thematisiert.
31
9
Eine symptomfreie 45-jährige Frau geht zur Krebsvorsorgeuntersuchung und lässt sich mittels einer
Mammografie untersuchen. Mit Hilfe der Gesundheitsstatistik lassen sich folgende Annahmen treffen:
Erstens die Wahrscheinlichkeit, dass eine symptomfreie Frau zwischen 40 und 50 Jahren Brustkrebs
hat, beträgt 1%; Zweitens die Wahrscheinlichkeit, dass diese Krankheit mit einer Mammografie erkannt
wird, liegt bei 80%; Drittens die Wahrscheinlichkeit, dass mit einer Mammografie Brustkrebs festgestellt wurde, obwohl die Krankheit gar nicht vorliegt, beträgt 9,6%. Wie groß ist die Wahrscheinlichkeit,
dass eine 45-jährige, symptomfreie Frau tatsächlich Brustkrebs hat, wenn sie einen positiven Mammografiebefund erhalten hat?36
Die meisten Menschen, auch Ärzte, schätzen die Wahrscheinlichkeit auf 70-80%. Allerdings
liegt die Lösung mit Hilfe des Wahrscheinlichkeitskalküls lediglich bei 7,8%.
Diese drei Beispiele ließen Kahneman und Tversky zu dem Ergebnis kommen, dass „solche
Resultate jeden entmutigen müssen, der die Menschen als vernünftige intuitive Statistiker
ansehen möchte“37. Als Erklärung führten sie die sogenannte Repräsentationsheuristik an.
In Hinblick auf die Beispiele der Münzwurfreihe und des Rouletterades bedeutet dies, dass
die zufällig aussehende Münzwurfreihe bzw. die Farbe Schwarz „repräsentativer“ für den
Zufall gehalten wird. Übertragen auf das dritte Beispiel heißt das, dass der positive Mammografietest (80% Wahrscheinlichkeit) stärker mit der Krankheit identifiziert wird als die
Krebs-Statistik für eine symptomfreie Frau zwischen 40 und 50 (1%).38
Neben der Kritik an den methodischen Schwächen in den Arbeiten Kahneman und Tverskys,
die vor allem auf die zu vage formulierte Repräsentationsheuristik zurückzuführen ist, wurde
vor allem die normative Setzung des richtigen Ergebnisses aus der Wahrscheinlichkeitstheorie kritisiert. Überhaupt wurde der Prozess, wie die Probanden auf das Ergebnis kamen,
nicht thematisiert. Ein falsches Ergebnis wurde direkt mit einem „bias“, also einer Verzerrung in Verbindung gebracht. Allerdings kann es dafür verschiedenste Gründe geben: Ob es
sich um unterschiedliche Interpretationen der Aufgabe, simple Rechenfehler oder um einen
wirklichen Denkfehler bzw. eine falsche Intuition handelt, konnte mit den Forschungen
Kahneman und Tverskys nicht beantwortet werden.39
Das Zustandekommen der Fehler spielt jedoch besonders in der Didaktik eine große Rolle.
In vielen didaktischen Untersuchungen wurden die Forschungen Kahneman und Tverskys
aufgegriffen und weiterentwickelt, sodass sie letztendlich zu einem Umdenken in der Lehrund Lernmethodik führten. Vor allem wurden die Schwierigkeiten der Modellbildung und
Mathematisierung diskutiert. Neben fachlichen Überlegungen wurden auch Diskussionen
Weitere Beispiele sind in Beck-Bornholdt; Dubben: Der Schein der Weisen. zu finden. Die anderen Beispiele
(vor allem am Anfang des Buches) eignen sich ebenso zum Einsatz im Unterricht. Allerdings sind die Schlussfolgerungen gegen Ende des Buches nicht differenziert genug.
36
Wassner; Biehler: Förderung Bayesianischen Denkens, S. 15.
37
Ebd. S. 16.
38
Ebd. S. 16.
39
Ebd. S. 19.
10
über die Grenzen und Möglichkeiten von formalen und intuitiven Lösungen erörtert. Immer
stärker wurde das Ziel ausgesprochen, die Schüler auf die Handlungs- und Entscheidungsfähigkeit (unter Unsicherheit) im späteren Leben vorzubereiten. Dabei sollen die Vorstellungen, die die Schüler mitbringen, aufgegriffen und weiterentwickelt werden.40 Dies kann
sowohl bedeuten, dass Widersprüche aufgezeigt und verändert werden als auch die Komplementarität von formalen und intuitiven Strategien berücksichtigt wird. Schließlich ist das
wechselseitige Zusammenspiel von Intuition und Wahrscheinlichkeitstheorie ein wichtiges
Ziel, dessen Erfüllung die Verbindung der psychologischen und der didaktischen Forschung
beinhaltet.41
Die Forschungen von Gerd Gigerenzer und von Christoph Wassner gehen in diese Richtung.42 Sie konzentrierten sich vor allem auf die bedingten Wahrscheinlichkeiten43 und fanden heraus, dass die Repräsentation der Aufgaben eine entscheidende Rolle spielt. Die numerischen Informationen wurden stets als Prozente, relative Häufigkeiten oder Wahrscheinlichkeiten formuliert.44 In diesem Format geben insbesondere auch die Medien (Fernsehen,
Zeitungen usw.) Informationen wieder. Wie oben angedeutet, fällt es dem menschlichen Gehirn schwer, mit diesem Repräsentationsmodell umzugehen. Es kann sich beispielsweise unter der Wahrscheinlichkeit, dass ein Prozent der symptomfreien Frauen trotzdem unter Krebs
leidet, nichts vorstellen. Anders zeigt sich dieser Sachverhalt, wenn er durch absolute Zahlen
wiedergegeben wird: Das Gehirn kann die Angabe „von hundert symptomfreien Frauen hat
eine Frau trotzdem Krebs“ durch das sogenannte natürliche Häufigkeitsformat45 intuitiv besser erfassen. Um diesen Unterschied zwischen relativen und natürlichen Häufigkeiten im
Bereich der bedingten Wahrscheinlichkeit aufzuzeigen, wird nachfolgend das Beispiel des
Mammografiebefundes mit Hilfe des natürlichen Häufigkeitsformtes umformuliert:46
„Stellen wir uns eine Welt vor, in der nichts über das Auftreten von Brustkrebs oder die Verlässlichkeit
von Testverfahren bekannt ist. In dem Fall könnte ein Diagnostiker nur aus seiner Erfahrung urteilen.
Nehmen wir an, ein Arzt hätte bisher 1000 symptomfreie 40 bis 50-jährige Frauen untersucht, von denen
10 Brustkrebs (B) hatten. Von den 10 kranken Frauen erhielten 8 ein positives Testergebnis (T+). Von
den 990 Gesunden waren 95 Testergebnisse positiv. Nun kommt eine 45-jährige symptomfreie Frau
40
Freudenthal war einer der ersten Didaktiker, der dies forderte. Vgl. Einleitung.
Gigerenzer: Repräsentation von Information, S. 123. .
Bentz: Empirische Untersuchungen, S. 2.
42
Einen Überblick liefert Gigerenzer; Todd: Simple Heuritics makes us smart.
43
Die Fehlurteile wurden nach Kahneman und Tverkeys Forschungen auf die Schwierigkeiten des Menschen
mit bedingten Wahrscheinlichkeiten zurückgeführt. Diese sind in der Literatur gut dokumentiert. Vgl. Eichler;
Vogel: Leitidee Daten und Zufall, S. 214.
44
Borovcnik erkannte das gleiche Problem, aber er arbeitete mit dem Chancenverhältnis. Vgl. Borovcnik:
Stochastik im Wechselspiel, S. 182.
45
Der Didaktiker Arthur Engel schlug bereits 1975 vor von einem Häufigkeitskonzept auszugehen. Er nannte
dies Wahrscheinlichkeitsabakus. Vgl. Engel: Stochastischer Abakus, S. 28.
46
Sedlmeier; Gigerenzer: Teaching Bayesian Reasoning, S. 393.
41
11
zum Arzt und will auch auf Brustkrebs getestet werden. Sie testet positiv. Wie groß ist die Wahrscheinlichkeit, dass sie Brustkrebs hat?“47
Mit Hilfe der Regeln von Bayes können sowohl für die relativen als auch für die natürlichen
Häufigkeiten Lösungen berechnet werden (Vgl. Abbildung 1):48
Abbildung 1:Wahrscheinlichkeiten und natürliche Häufigkeiten.
Quelle: Wassner; Martignon; Biehler: Bayesianisches Denken, S. 62.
Hieraus wird deutlich, dass im Repräsentationsformat der natürlichen Häufigkeiten ein reines Abzählen von günstigen und möglichen Fällen verwendet wurde. Der Satz von Bayes
wird nicht benötigt bzw. kann als Ergebnis festgehalten werden. Im Falle der relativen Häufigkeiten bzw. der Prozente führt die Beobachtung der 1.000 Patienten zu einer Schätzung a
posteriori, die mehr oder weniger repräsentativ für die nächsten Untersuchungen stehen soll.
Mit dem gleichen Prinzip werden auch die weiteren Werte entwickelt. Beispielsweise wird
eine bestimmte Anzahl von Brustkrebserkrankten getestet und beobachtet, wie oft der Test
ein positives Ergebnis anzeigt. Dadurch wird deutlich, dass es sich bei den unterschiedlichen
Lösungsansätzen um verschiedene Wahrscheinlichkeitsbegriffe handelt. Während das Konzept der relativen Häufigkeiten von einem frequentistischen Wahrscheinlichkeitsbegriff ausgeht und die verschiedenen numerischen Werte damit (zwangsläufig) unabhängig voneinander in verschiedenen Experimenten entstehen, bezieht sich das Konzept der natürlichen Häufigkeiten auf den subjektiven Wahrscheinlichkeitsbegriff, der seine Informationen aus einem
einzigen Experiment zieht. Dies hat zum Vorteil, dass die Basisrate (z. B. 8 von 10 kranken
Frauen erhielten einen positiven Testbefund) berücksichtigt wird. Durch die Umdeutung der
relativen Häufigkeiten zu Wahrscheinlichkeiten werden die Schüler gezwungen auf den Satz
von Bayes zurückzugreifen, um die bedingte Wahrscheinlichkeit P(B|M₊) auszurechnen.49
Die in vielen Bereichen sinnvolle Bildung von Kongruenzklassen bei relativen Häufigkeiten
47
Wassner; Biehler: Förderung Bayesianischen Denkens, S. 15.
Hierbei steht B für Brustkrebs und M₊ für einen positiven Mammografietest. Vgl. Wassner; Martignon;
Biehler: Bayesianisches Denken, S. 62.
49
Ebd. S. 22.
48
12
hat im Gebiet der Statistik gravierende Folgen. Menschen erkennen, wie im Krankenhaus7
70
7
beispiel, nicht den Unterschied von „7 von 10“ (10) und „70 von 100“ (100 = 10). Diese Vernachlässigung des Nenners und damit der Stichprobengröße wird in vielen Statistiken ausgenutzt:
„In Werbungen liest man beispielsweise, dass ein gewisses Medikament das Risiko einer bestimmten
Krankheit um die Hälfte reduziert, ohne dass man erfährt, was das absolute Risiko ist.“ 50
Diese Probleme können durch das natürliche Häufigkeitskonzept abgebaut werden, da empirische Untersuchungen zeigten, dass Menschen mit Hilfe natürlicher Häufigkeiten besser
mit Unsicherheiten und stochastischen Fragestellungen umgehen können.51
Neben der Häufigkeitsinterpretation unterstützen visuelle Darstellungen die menschliche Intuition. Die in der Stochastik am häufigsten verwendeten Werkzeuge sind Baumdiagramme,
Urnen, Vierfeldertafeln und Venn-Diagramme.52 Die Auswahl der Visualisierungen hängt
von der Art der Aufgabe und dem Lerntyp ab. Grundsätzlich sollte das Werkzeug möglichst
nahe an der Realität bzw. der Aufgabenstellung liegen, um die Intuition zu unterstützen.53
Dennoch dienen das Häufigkeitskonzept und die graphische Veranschaulichung lediglich als
Hilfestellung zur Modellierung bzw. zur Veranschaulichung stochastischer Probleme.
Dadurch kann das Verständnis der Wahrscheinlichkeitsbegriffe verbessert werden. Auch
können gegebenenfalls Paradoxa aufgelöst und ein besseres, intuitives Entscheiden ermöglicht werden. Dabei wird häufig der subjektive Wahrscheinlichkeitsbegriff verwendet. Allerdings stellt der Zusammenhang von relativen Häufigkeiten und Wahrscheinlichkeiten, der
auf dem empirischen bzw. schwachen Gesetz der großen Zahlen basiert, eine „fundamentale
Idee“ des Stochastikunterrichts dar und darf auf keinen Fall vernachlässigt werden.54 Ebenso
spielt der Laplace-Wahrscheinlichkeitsbegriff eine große Rolle in Glücksspielen und somit
im Alltag der Schüler. Eine Nichtbeachtung des subjektiven Wahrscheinlichkeitsbegriffs
(vgl. Lehrplan) sowie eine zu starke Konzentration auf die objektiven Wahrscheinlichkeitsbegriffe, führen nicht zum Ziel, da die Vorstellungen der Schüler vernachlässigt werden.
Daher sollte es zu einem Zusammenspiel der Wahrscheinlichkeitsbegriffe kommen:55 Den
50
Latten; Martignon; Monti; Multmeier: Förderung erster Kompetenzen, S. 22.
Gigerenzer: Einmaleins der Skepsis, S. 68
Kurz-Milcke, Gigerenzer, Martignon: Risiken durchschauen, S. 11.
52
Wassner; Biehler: Förderung Bayesianischen Denkens, S. 24.
53
Wassner; Martignon; Biehler: Bayesianisches Denken, S. 61.
54
Prediger: Do you want, S. 145.
55
Hefendehl-Hebeker: Didaktik der Stochastik, S. 13.
51
13
Schülern sollen die Chancen und Risiken der Wahrscheinlichkeitsbegriffe (Laplace, frequentistisch und subjektiv) bewusst werden, um so den jeweils sinnvolleren zur Modellierung auszuwählen.
Insgesamt kann die eingangs gestellte Frage, ob Menschen gute Statistiker sind, eher verneint werden. Sie können relative Häufigkeiten und Wahrscheinlichkeiten intuitiv nur
schlecht verarbeiten und benötigen Hilfestellungen, wie das natürliche Häufigkeitskonzept
oder graphische Darstellungen. Insbesondere zeigten die erwähnten Forschungen, dass Menschen durch die Häufigkeitsinterpretation zu guten intuitiven Wahrscheinlichkeitsschätzungen kommen können, ohne mit der Wahrscheinlichkeitstheorie übermäßig vertraut zu sein.56
Im Alltag greifen Menschen oft auf ihre intuitiven Vorkenntnisse zurück, vernachlässigen
bekannte Hilfsmittel sowie die in der Schule erlernte Wahrscheinlichkeitstheorie. Dennoch
ist es nicht das Ziel, die intuitiven Vorstellungen der Schüler auszuklammern und sozusagen
„von vorne anzufangen“57, da sie ihr Wissen im Alltag anwenden sollen. Dies kann nur geschehen, wenn der Unterricht Mathematik und Intuition miteinander verbindet.58 Die vielen
Fehlvorstellungen und Paradoxa der Stochastik zeigen, dass sich viele Menschen (auch sehr
begabte Mathematiker) in diesem Bereich irren.59 Dies veranlasste auch Laplace zum Ausspruch: „Einer der großen Vorteile der Wahrscheinlichkeitsrechnung ist der, dass man lernt,
dem ersten Anschein zu misstrauen.“60 Es ist also nicht schlimm, dass die Schüler und Lehrkräfte anfangs intuitiv falsche Vorstellungen haben. Fehler können sogar für den weiteren
Verlauf des Unterrichts fruchtbar sein. Allerdings benötigt es eine intensive Auseinandersetzung mit Zufallsprozessen, um diese zu modifizieren. Es kann also nicht hilfreich sein,
aus dem Wahrscheinlichkeitskalkül Formeln bereitzustellen und den Schülern das richtige
Ergebnis zu zeigen. Stochastikunterricht „will ja nicht zur nachträglichen Besserwisserei erziehen, sondern vorbeugen, die Intuition zurechtrücken und ein wenig immunisieren.“61
Wie stark die intuitiven Vorstellungen und wie schwer eine Modifizierung dieser ist, repräsentiert besonders das sogenannte Ziegenproblem:
Ein Kandidat hat die Möglichkeit aus drei Türen eine auszuwählen. Hinter zwei der drei Türen versteckt
sich eine Ziege und hinter der dritten ein Auto. Nach der Wahl des Kandidaten wird eine Tür geöffnet,
hinter der eine Ziege steht. Nun besteht die Möglichkeit die Tür zu wechseln. Sollte man das tun?
Als Marilyn vos Savant, eine US-Amerikanerin mit einem der höchsten Intelligenzquotienten, das Wechseln empfahl und sogar die korrekte Wahrscheinlichkeit für einen Gewinn
56
Cosmides; Tooby: Are Humans good, S. 69.
Büchter; Hußmann; Leuders; Prediger: Zufall im Griff, S. 2.
58
Ebd. S. 2
59
Freudenthal: Wahrscheinlichkeit und Statistik, S. 532.
60
Winter: Zur intuitiven Aufklärung, S. 23.
61
Führer: Misstrauensregeln, S. 63.
57
14
2
durch Wechseln mit angab, wurden ihr viele Leserbriefe zugeschickt, die ihr widersprachen
3
(einen sogar von der Research Mathematical Statistican der National Institutes of Health).
Die Widersprüche nahmen auch nach zwei weiteren sinnvollen Erklärungsversuchen (Auswahl aus 100 Türen, die alle bis auf zwei geöffnet werden und Aufzählen aller Möglichkeiten
nach der Wahl der Tür) nicht ab. Ob der letzte Erklärungsversuch durch die Simulation der
Situation gelang, ist nicht bekannt. Allerdings können Simulationen des Ziegenproblems
durchaus überzeugend wirken.62 Hieran ist zu erkennen, wie stark die subjektiven Voreinstellungen sind. Reines Erklären der Situation baut diese Fehlvorstellung nicht ab. Es ist
notwendig, dass Schüler ihre intuitiven Lösungen selbst reflektieren. Dies benötigt Zeit und
darf nicht unter dem Druck einer Notengebung geschehen.63
Ebenso zeigt sich dies beim Roulette-Spiel. Auch wenn die Schüler gelernt haben, dass der
Roulette-Wurf unabhängig von den vorhergegangenen Ergebnissen ist, werden sie dennoch
in Versuchung geraten bei zehnmaligem Rot, im nächsten Wurf auf Schwarz zu setzen. Daher sollten auch im Unterricht Kenntnisse aus der Psychologie, wie die Repräsentationsheuristik und die Reflexion des gewählten Wahrscheinlichkeitsbegriffes diskutiert werden.64 So
wird an Stelle von statistischen Ritualen statistisches Denken gelehrt.65 Dabei sollte es zu
einem dynamischen Wechselspiel zwischen Intuition und mathematischer Theorie kommen,
in dem die Intuition Ausgangspunkt des Prozesses ist. Repräsentationsformate wie die natürliche Häufigkeit und graphische Visualisierungen können dabei die Verbindung darstellen. Allerdings müssen diese ebenfalls reflektiert werden, denn nicht immer sagt „ein Bild
mehr als 1.000 Worte“.66
Im Folgenden werden die inhaltlichen Wahrscheinlichkeitsmodelle (Laplace, frequentistisch, subjektiv) auf ihre Chancen und Grenzen analysiert. Dabei wurde ein genetischer Zugang gewählt, den die Schüler mit Hilfe von Arbeitsblättern67 durchlaufen. Die psychologischen Erkenntnisse, die in diesem Kapitel dargestellt wurden, bildeten die Basis zur Erstellung der Arbeitsblätter. Den Schülern soll bewusst werden, dass Menschen Probleme beim
intuitiven Einschätzen stochastischer Problemstellungen haben. Darüber hinaus sollen die
62
Wollring: Beispiel zur Konzeption, S. 12.
Zimmermann; Gundlach: Wie Ziegen, S. 322.
63
Jahnke: Drei Türen, S. 48.
Lind: Zum Wahrscheinlichkeitsbegriff, S. 39.
Krauss; Atmaca: Wie man Schülern, S. 38.
Anschauliche Darstellung in: Randow: Ziegenproblem.
64
Büchter; Hußmann; Leuders; Prediger: Zufall im Griff, S. 5.
65
Gigerenzer: Die Evolution, S. 18.
66
Gigerenzer; Martignon: Risikokompetenz, S. 96.
67
Die Arbeitsblätter befinden sich im Anhang.
15
Schüler lernen mit Unsicherheit umzugehen, die sich aus den Grenzen der inhaltlichen
Wahrscheinlichkeitsbegriffen ergibt. Dabei wird thematisiert, wie die Mathematik bzw. die
Axiomatik Kolmogorovs auf diese Grenzen reagiert. Auf diese Weise entsteht das geforderte
wechselseitige Zusammenspiel zwischen Theorie und Intuition.
3. Ein alternativer Zugang zur Stochastik
3.1 Der Einstieg in die Stochastik – Die Wahrscheinlichkeitsbegriffe
Zum Einstieg in die Stochastik wird der der Riemer-Quader (Aufgabe 1) verwendet, der
mittlerweile einen Klassiker zum Einstieg in die Stochastik darstellt.68 Das Ziel ist es nicht,
Formeln (wie zum Beispiel die Formel zur Berechnung der Laplace-Wahrscheinlichkeit) zu
erarbeiten, sondern zentrale stochastische Ideen herauszuarbeiten, die dann vertieft werden.
Damit steht das Mathematisieren bzw. das Modellieren von Anwendungssituationen eindeutig im Vordergrund. Auch wenn die Axiomatik Kolmogorovs in der Universitätsmathematik
die Ausgangslage darstellt, sollte in der Schule der Fokus auf der Modellierung von Anwendungen liegen. So lernen Schüler nicht nur Formeln auswendig, sondern erfahren wie Sachverhalte mit Hilfe der Mathematik beschrieben werden können. Daher erfolgt der Einstieg
in die Stochastik nicht mit der mathematischen Definition der Wahrscheinlichkeit als ein
normiertes, additives Maß auf einer Ereignisalgebra. Dies würde bei den Schülern auf Unverständnis stoßen. Zu Beginn sollten eher der Anwendungsbezug und die inhaltliche Deutung einer Wahrscheinlichkeit stehen. Dies entspricht ebenso der historischen Entwicklung
der Stochastik, in der das wechselseitige Ergänzen von Theorie und Praxis deutlich zu erkennen ist.69
Der Riemer-Quader stellt durch seinen experimentellen und anschaulichen Zugang eine geeignete erste Aufgabe dar. Die Schüler versuchen mit Hilfe der inhaltlichen Wahrscheinlichkeitsbegriffe Wahrscheinlichkeitsschätzungen abzugeben. Ein wichtiges Ziel der Aufgabe
ist es, dass die Schüler erkennen, dass sowohl der Laplace-, der frequentistische als auch der
subjektive Wahrscheinlichkeitsbegriff lediglich Modelle sind, um die Realität abzubilden.70
Es geht daher in der Aufgabe um die Erkundung der inhaltlichen Wahrscheinlichkeitsbegriffe und nicht um deren Systematisierung. Erkunden bedeutet hier Wege zu finden, um
68
Riemer: Stochastische Probleme, S. 31.
Büchter; Henn: Elementare Stochastik, S. VI.
Kütting: Didaktik der Stochastik, S. 62.
70
Schupp: Zum Verhältnis, S. 218.
69
16
Wahrscheinlichkeiten zu gewinnen und mit ihnen zu rechnen. Was Wahrscheinlichkeit in
mathematischem Sinne (Axiomatik Kolmogorovs) ist, wird hier noch nicht ersichtlich.71
In Aufgabenteil 1a) sollen die Schüler die Wahrscheinlichkeiten für den gewöhnlichen Würfel und den Riemer-Quader a priori schätzen. Beim gewöhnlichen Würfel ist die LaplaceAnnahme (die Annahme einer Gleichwahrscheinlichkeit auf Grund der Symmetrieeigenschaften) naheliegend. Allerdings werden intuitive Vorstellungen wie „ich weiß aus verschiedenen Spielen, dass die 6 schwieriger zu würfeln ist als die anderen Zahlen“ nicht ausgeblendet (subjektiver Wahrscheinlichkeitsbegriff).
Beim Riemer-Quader wird der hypothetische Charakter der Wahrscheinlichkeit deutlich. Im
Gegensatz zum Würfel sind prinzipiell mehrere Hypothesen gültig und können nicht a priori
verworfen werden. Eine erste Schätzung der Wahrscheinlichkeit kann beim Riemer-Quader
genauso wie beim gewöhnlichen Würfel abgeben werden: Es ist möglich, sich allein vom
subjektiven Empfinden leiten zu lassen, um so Wahrscheinlichkeiten zu bestimmen. Allerdings können die Schüler auch durch theoretische Überlegungen (Bestimmung des Verhältnisses der Flächen zueinander) erste Einschätzungen der Wahrscheinlichkeit abgeben. Das
Experimentieren mit den Würfeln (frequentistischer Wahrscheinlichkeitsbegriff) wurde bewusst in Aufgabe 1b) verschoben, da den Schülern so der große Nachteil des frequentistischen Modells deutlich wird: Mit diesem Modell können die Wahrscheinlichkeiten lediglich
a posteriori bestimmt werden. Die Schüler würden vermutlich ohne diese Trennung in der
Aufgabenstellung direkt anfangen zu experimentieren, sodass ihre Intuition oder theoretische Überlegungen unberücksichtigt bleiben würden.
Beim Experimentieren in Aufgabe 1b) werden die Schüler möglicherweise sowohl den gewöhnlichen Würfel als auch den Riemer-Quader verwenden. Beim gewöhnlichen Würfeln
ist diese Versuchsreihe eigentlich nicht notwendig, falls die theoretischen Überlegungen des
Laplace-Wahrscheinlichkeitsbegriffs vollzogen wurden.72 Allerdings sollte den Schülern der
Raum für Experimente gegeben werden. Sie sollten selbst erkennen, dass die relative Häufigkeit sich mit steigender Versuchszahl immer stärker an ihren bereits vermuteten Wert
1
6
annähert (empirisches Gesetz der großen Zahlen). Das empirische Gesetz der großen Zahlen
stellt somit ein Naturgesetz dar, das durch induktives Schließen ermittelt wurde.73
Allerdings könnten einige Schüler behaupten, dass der Würfel durch fehlerhafte Herstellung,
Abnutzung oder Ähnliches kein Laplace-Würfel sei und so die kleinen Abweichungen von
71
Eichler; Vogel: Leitidee Daten und Zufall, S.148.
Riemer: Mit Bleistiften würfeln, S. 30 PM.
73
Engel: Wahrscheinlichkeitsrechnung und Statistik, S. 23.
72
17
1
begründen. Diese Begründungen sollen in einer Diskussion über die Voraussetzungen des
6
Laplace-Wahrscheinlichkeitsbegriffs münden. Dadurch werden sowohl der Modellcharakter
als auch die Annahme der Gleichwahrscheinlichkeit aus dem Prinzip des „unzureichenden
Grundes“ deutlich. Die Ergebnisse hängen also stark von den verwendeten Modellen ab. Ziel
ist es, die unterschiedlichen Ergebnisse zu erläutern und so einen wesentlichen Beitrag zur
Allgemeinbildung im Mathematikunterricht zu leisten.74
Dagegen gilt beim Riemer-Quader das Prinzip der Gleichwahrscheinlichkeit von Flächenverhältnissen nicht. Die plausiblen, theoretischen Überlegungen, die Wahrscheinlichkeit
über das Verhältnis der Seitenflächen zu berechnen, halten einer empirischen Überprüfung
nicht stand. Dadurch erkennen die Schüler, dass das Laplace-Modell verworfen werden muss
und übernehmen die relativen Häufigkeiten als Wahrscheinlichkeiten (frequentistischer
Wahrscheinlichkeitsbegriff). Dabei ist es den Schülern freigestellt, wie oft sie „würfeln“
möchten. Ihnen wird auffallen, dass die Schätzungen besser werden, je häufiger sie werfen.
Daher wird die beste Schätzung durch die Zusammenführung der Versuche der gesamten
Klasse erreicht. Dies macht die Bedeutung der Versuchsanzahl bzw. des Stichprobenumfangs deutlich. Außerdem kann dies als Vorbereitung für eine geplante Computersimulation
genutzt werden. Simulationen sind unabdingbar, wenn die Wahrscheinlichkeitstheorie über
die endlichen Laplace-Wahrscheinlichkeitsräume hinausgehen soll.75
Der Quaderwürfel hat gegenüber anderen Zufallsgeneratoren (z. B. Werfen von Reißbrettstifte) einen großen Vorteil: Die Schüler können ihre Überlegungen zum Laplace-Wahrscheinlichkeitsbegriff einbringen und argumentieren, dass die gegenüberliegenden Seiten
gleichwahrscheinlich sein müssten. Dafür sprechen auch die empirischen Werte, die sich nur
wenig voneinander unterscheiden. Daher werden die relativen Häufigkeiten nicht komplett
übernommen, sondern in der zweiten Zeile der Tabelle 2 angepasst.76
Tabelle 2: Schätzungen Quaderwürfel.
Augenzahl
Schätzung der Wahrscheinlichkeit (1000 Würfe)
Neue Schätzung der Wahrscheinlichkeit
1
0,03
2
0,10
3
0,35
4
0,40
5
0,08
6
0,04
0,03
0,09
0,38
0,38
0,09
0,03
Quelle: Eichler; Vogel: Leitidee Daten und Zufall, S.150.
74
Götz; Humenberger: Problem des anderen, S. 51.
Biehler; Maxara: Integration, S. 46.
76
Eichler; Vogel: Leitidee Daten und Zufall, S. 150.
75
18
Im Gegensatz zum Werfen von Reißbrettstiften wird deutlich, dass es sich bei der Übernahme der relativen Häufigkeiten um eine Schätzung bzw. ein Modell handelt. Bei den Reißbrettstiften ist dies nicht offensichtlich, da es zu den relativen Häufigkeiten keine Alternative
gibt und sie daher übernommen werden müssen. Dadurch sind Schwankungen ab einer gewissen Wurfanzahl unerwünscht, da ein objektiver Wert (ähnlich wie beim Laplace-Wahrscheinlichkeitsbegriff) erreicht werden soll. Beim Riemann-Quader hingegen wurden die
Wahrscheinlichkeiten durch eine Modifikation der relativen Häufigkeiten bestimmt.77
Generell ist es gleichgültig, welchen Zugang bzw. welches Modell die Schüler anfangs wählten, da es für alle drei Modelle genügend plausible Argumente gibt. Der Fokus sollte eher
auf der Reflexion der Modelle liegen und gegebenenfalls durch theoretische oder empirische
Überlegungen modifiziert werden.78
Die zweite Aufgabe soll diese Begriffsbildung unterstützen. Das historische Beispiel der
„Wette des Chevalier“ soll die Schüler erkennen lassen, dass bereits im 17. Jahrhundert diese
drei Möglichkeiten zur Bestimmung einer Wahrscheinlichkeit angewandt wurden. Die „Geburt der Stochastik“ als Ausgangspunkt des stochastischen Lernprozesses zu setzen, hat den
Vorteil, dass die Parallelen zwischen individuellem und gesamtmenschlichem Erkenntnisprozess deutlich werden. Die Schüler können nach und nach die Entwicklung der Mathematik nachvollziehen. Dabei sind es vor allem die historischen Probleme, die einen großen Anwendungsbezug haben und somit motivierend auf die Schüler wirken.79
An diesem Punkt des Unterrichtes geht es noch nicht darum das Problem des Chevaliers (mit
Hilfe des Laplace-Wahrscheinlichkeitsbegriffs) zu lösen, sondern mögliche Lösungswege
zu diskutieren. Ausgangspunkt ist dabei wieder die Intuition der Schüler. Sie überlegen sich,
ob sie die Wette des Chevaliers annehmen sollen (Aufgabe 2a).80 In dieser Situation wird
der subjektive Wahrscheinlichkeitsbegriff verwendet. Es geht vor allem darum einzuschätzen, ob der Chevalier die größere Gewinnwahrscheinlichkeit hat. Der prognostische sowie
der hypothetische Charakter der Wahrscheinlichkeit werden dadurch deutlich.81
Im nächsten Schritt (Aufgabe 2b) sollen sich die Schüler in die Situation des Chevalier de
Méré hineinversetzen und analysieren, wie er Wahrscheinlichkeiten ermittelt: Aus bereits
vorhergegangenen Versuchserfahrungen (frequentistischer Wahrscheinlichkeitsbegriff)
77
Riemer: Stochastische Probleme, S. 21.
Eichler; Vogel: Leitfaden Stochastik, S. 105.
Wirths: Harmonietest, S. 16.
78
Eichler; Vogel: Leitidee Daten und Zufall, S. 148.
79
Steinbring: Mathematische Begriffe, S. 94.
80
Zur Beschreibung der Wette vgl. Kapitel „Sind Menschen gute Statistiker“.
81
Riemer: Elementare Stochastik, S. 35.
19
wusste er, dass seine Gewinnwahrscheinlichkeit größer als die seines Gegners war, wenn er
auf eine 6 in vier Würfen setzte. Die Kombination aus der Laplace-Annahme (Gewinnwahr1
1
scheinlichkeit von 6 bei einem Wurf bzw. 36 für eine Doppel-6) und die Proportionalitätsannahme der Wahrscheinlichkeit führten zu dem Schluss, dass er auch bei 24 (= 4∙6) Würfen
öfter gewinnen würde. Es ist wichtig, dass die Schüler erkennen, dass sich der Chevalier
trotz plausibler Argumente irrte. Dadurch sollen die Schüler zur Einsicht gelangen, dass auch
intelligente Menschen keine fehlerfreie Intuition in stochastischen Fragestellungen haben
und fehlerhafte erste Vermutungen kein Problem darstellen. Andererseits erlernen die Schüler dabei auch Fremdverstehen. Dadurch soll ein Überheblichkeitsgefühl der Schüler gegenüber anderen Zeiten und Kulturen vorgebeugt werden.82
Auch Aufgabe 2c) folgt dem historischen Verlauf. Der Chevalier bemerkte nach ein paar
Spielen, dass er öfter verlor als gewann. Die Versuchsanzahl wurde hier ganz bewusst weggelassen. Allerdings ist die Versuchslänge der entscheidende Faktor, ob der Chevalier seiner
Intuition oder seiner Versuchserfahrung vertrauen sollte. Falls dieses Bewusstsein bei den
Schülern noch nicht entwickelt sein sollte, können sie diese Aufgabe dennoch bewältigen:
Die Überprüfung der Voraussetzung der Gleichwahrscheinlichkeit aller Versuchsereignisse
führte beim Riemer-Quader in Aufgabe 1 zur Verwerfung des Laplace-Wahrscheinlichkeitsmodell. Sehen die Schüler dazu keinen Anlass, werden sie sich für die Intuition de Mérés
entscheiden. Sind sie hingegen nicht davon überzeugt, werden sie beginnen zu experimentieren und erkennen, dass der Stichprobenumfang eine große Rolle spielt. Da dieser allerdings nicht angegeben ist, werden die Schüler eine Versuchsreihe starten. Dies bearbeiten
die Schüler in der Vertiefungsaufgabe und können in der nächsten Stunde damit weiterarbeiten. So wird deutlich, wie stark die Verbindung von Theorie und Praxis im Bereich der
Stochastik ausgeprägt war. Wie in der historischen Genese sollen die Schüler in der Folge
erforschen, wie man a priori mit Hilfe des Laplace-Wahrscheinlichkeitsmodells Wahrscheinlichkeiten berechnen kann. Gleichzeitig sollen ihnen aber auch die Grenzen dieses
Konzeptes bewusst werden. Somit erschließen sich die Schüler die Stochastik entlang der
historischen Entwicklung.83
Den Abschluss des Einstiegs in die Stochastik bildet eine Zusammenfassung der bisherigen
Erkenntnisse (Aufgabe 3). Zunächst untersuchen die Schüler, wie Wahrscheinlichkeiten bestimmt werden können (Laplace-, frequentistischer und subjektiver Wahrscheinlichkeitsbegriff). In Aufgabe 3b) werden diese Wahrscheinlichkeitsmodelle erstmals auf Chancen und
82
83
Glickman: Warum man, S. 44.
Gigerenzer: Die Evolution, S. 3.
20
Grenzen analysiert. Dazu erhalten die SuS eine Tabelle, die im Laufe der Reihe vervollständigt werden soll, sodass die Schüler sich mit den Wahrscheinlichkeitsbegriffen argumentativ
auseinandersetzen können.84
Besonders die Unterschiede zwischen den objektiven (Laplace- und frequentistischer Wahrscheinlichkeitsbegriff) und dem subjektiven Wahrscheinlichkeitsbegriff werden bereits an
dieser Stelle deutlich: Bei den objektiven Wahrscheinlichkeitsbegriffen hängt die Schätzung
der Wahrscheinlichkeit von den Versuchsbedingungen ab. Fragestellungen wie „Ist eine
Gleichwahrscheinlichkeit der Ereignisse a priori anzunehmen?“ oder „Sind die Versuche
wirklich unabhängig voneinander?“ sind hier elementar. Dagegen hängen die subjektiven
Wahrscheinlichkeiten von der Person und deren Wissensstand ab.85
Natürlich muss die Lehrkraft an einigen Stellen die Begriffe vorgeben, die von den Schülern
nicht entdeckt werden können. Dazu zählen die Begriffe Laplace-, frequentistischer und subjektiver Wahrscheinlichkeitsbegriff, aber auch das Prinzip des unzureichenden Grundes und
das empirische Gesetz der großen Zahlen.86 Jedoch sind diese Begriffe (fast) selbsterklärend
und spiegeln den Lernprozess der Schüler wider. Damit werden die Begriffe nicht zum
Selbstzweck eingeführt, sondern strukturieren die Tätigkeiten der Schüler.
3.2 Der Laplace-Wahrscheinlichkeitsbegriff
3.2.1 Arbeitsblatt I - Berechnung von Laplace-Wahrscheinlichkeiten
Die Schüler lösen in der ersten Aufgabe dieses Arbeitsblattes das Problem des Chavaliers,
in dem sie sich in die Rolle von Fermat/ Pascal versetzen. Dabei finden sie heraus, welchen
Weg die Mathematik gehen musste, um zu neuen Erkenntnissen zu gelangen. Der Mathematik wird so die Künstlichkeit eines ahistorisch vermittelten Fertigprodukts genommen.87
Die genetische Herangehensweise, den Laplace-Wahrscheinlichkeitsbegriff an den Anfang
zu setzen, spiegelt sowohl das deterministische Verständnis der Zeit von Pascal und Fermat
als auch das Bild von Mathematik der Schüler wider.
Zunächst sollen die Schüler erkennen, dass es wesentlich leichter ist ein Ersatzproblem (der
Chevalier verliert) zu lösen. Sowohl diese Anwendung der Gegenwahrscheinlichkeit als
84
Eine ausgefüllte Tabelle befindet sich im Anhang.
Eichler; Vogel: Leitidee Stochastik, S. 207.
86
Ebd. S. 154.
87
Kütting; Sauer; Padberg: Elementare Stochastik, S. 82.
85
21
auch die Pfad- und Summenregel sind für die Schüler intuitiv einleuchtend. Die Formulierung dieser in Form der Axiomatik Kolmogorovs ist nicht notwendig. Das Problem des Chevaliers kann auf diese Weise relativ leicht gelöst werden.88
Ziel der Aufgabe 1b) und vor allem der Aufgabe 2 ist die Entdeckung der Grundidee des
Abzählens durch die Formel
Günstige
Mögliche
. Dazu beschreiben die Schüler mit Hilfe der Mengen-
schreibweise ein Zufallsexperiment. Alle möglichen Ergebnisse werden durch ω beschrieben und in der Ergebnismenge Ω = {ω| ω ist Ergebnis des Zufallsexperiments}zusammengefasst. Die Festlegung der Ergebnismenge ist subjektiv, da beispielsweise bei der Wette des
Chevaliers die Ergebnismenge durch Ω1 = {1, 2, 3, 4, 5, 6}oder durch Ω2 = {6, keine 6}
definiert werden kann. Ist die Ergebnismenge wie in den obigen Beispielen endlich, kann sie
zu Ω = {ω1, ω2,…, ωn} vereinfacht werden. Das Laplace-Modell mit der endlichen Ergebnismenge als Voraussetzung bietet sich daher für diesen Formalitätsaspekt an.89
Damit die Schüler nicht durch ein zu schwieriges Problem und durch den Formalitätsaspekt
überfordert werden, wird zur Unterstützung in Aufgabe 2 das Werfen mit zwei LaplaceWürfeln bearbeitet. Der Laplace-Würfel wurde von den Schülern bereits auf dem Arbeitsblatt „Einstieg in die Stochastik“ analysiert. Jetzt wird das Werfen mit zwei Würfeln betrachtet, da im Gegensatz zum Werfen eines Würfels mehrere zunächst plausible Ergebnismengen existieren. Die Schüler erkennen also, dass die Beschreibung eines Zufallsexperiments mit Hilfe einer Ergebnismenge ein Modell darstellt, das reflektiert werden muss. Die
Ergebnismenge bzw. der Wahrscheinlichkeitsraum stellt „ein Scharnier zwischen einem realen (oder auch fiktiven, aber in der Realität vorgestellten, auf die Realität bezogenen, aus
der Realität idealisierten) Kontext und der mathematischen Begrifflichkeit“90 dar. Insbesondere beim Laplace-Ansatz, bei dem alle Elementarereignisse gleichwahrscheinlich sein müssen, spielt dieser Aspekt eine große Rolle. Außerdem wird durch die Betonung des LaplaceModells ersichtlich, dass die Schüler dieses Modell in der Aufgabe erkunden sollen. Damit
ist klar, dass in dieser Aufgabe sowohl der subjektive als auch der frequentistische Wahrscheinlichkeitsbegriff nicht herangezogen werden sollen.
88
Möglichst alle Schüler sollen ein Erfolgserlebnis am Anfang dieser Reihe haben, sodass in den Hilfestellungen die Entdeckung der Eigenschaften der Wahrscheinlichkeit angestoßen wird. Dabei wird darauf geachtet,
dass die Schüler die vorgeschlagene Herangehensweise stets begründen. So soll es nicht zu einem reinen Nachvollzug, sondern zur Reflexion des Lösungsweges und des gewählten Modells kommen. Vgl. Biehler; Engel:
Stochastik, S. 235.
89
Büchter; Henn: Elementare Stochastik, S. 162.
Basler: Grundbegriffe der Wahrscheinlichkeitsrechnung, S. 4.
Büchter; Henn: Stochastische Modellbildung, S. 33.
Engel: Wahrscheinlichkeitsrechnung und Statistik, S. 14.
90
Bender: Grundvorstellungen und Grundverständnisse, S. 11.
22
Durch die Einbettung der Aufgabe 2 „Werfen mit zwei Würfeln“ in den Gesellschaftsspielklassiker „Die Siedler von Catan“ wird die Intuition der Schüler miteinbezogen. Viele Schüler werden das Spiel gespielt haben und deshalb die große Bedeutung der Augenanzahl 7
kennen. Neben diesem emotionsbezogenen Vorteil der Einbettung in das Gesellschaftsspiel,
bietet die graphische Aufmachung (unterschiedliche Größe der Zahlen auf den Spielkarten)
eine Visualisierung der Laplace-Wahrscheinlichkeiten.91
Die Schüler berechnen (nach einer Schätzung) die Wahrscheinlichkeit einer 7 durch das Abzählprinzip.92 In Aufgabenteil 2c) wird der Lösungsweg der Schüler vertieft und durch die
Mengenschreibweise formalisiert, indem drei verschiedene Ergebnismengen angegeben
werden.93 Diese Ergebnismengen führen durch verschiedene Zählprinzipien zu verschiedenen Wahrscheinlichkeiten. Die Schüler sollen diese analysieren und das Prinzip der Berechnung von Laplace-Wahrscheinlichkeiten reflektieren: 94
Ω1 = {(1,1), (1,2),…, (1,6), (2,2), (2,3),…, (4,6), (5,5), (5,6), (6,6)} mit |Ω1| = 21, sodass P(7) =
1
21
Ω2 = {(1|1), (1|2),…, (1|6), (2|1), (2|2),…, (5|5), (5|6), (6|1), . . . (6|6)} mit |Ω 2| = 36, sodass P(7) =
Ω3 = {2, 3, 4,…, 10, 11, 12} mit |Ω3|= 11, sodass P(7) =
1
11
.
1
36
.
.
Alle genannten Ergebnismengen sind zunächst plausibel, doch nur für Ω2 ist das LaplaceModell sinnvoll.95 Erst die Reflexion der Situation mit Hilfe der Abbildung 2 macht dies
sichtbar:
Abbildung 2: Würfelmöglichkeiten.
Quelle: Landungsbildungsserver Baden-Württemberg.
91
Prediger: Auch will ich, S. 34.
Auch in dieser Aufgabe werden aus Differenzierungsgründen Hilfestellungen gegeben.
93
Schöner wäre es, wenn auf die Ergebnismengen der Schüler zurückgegriffen werden könnte, da die Reflexion
der eigenen Lernprodukte einen höheren Lernerfolg mit sich bringen würde. Vgl. Schanz: Statistik und Wahrscheinlichkeitsrechnung, S. 43.
94
Zunächst sind alle Ergebnismengen prinzipiell zugelassen. Erst später werden die nicht sinnvollen Hypothesen verworfen (z.B. durch Experimentieren). Jahnke bezeichnet dies als hypothetisch-deduktive Vorgehensweise. Vgl. Jahnke: Beweisen, S. 11.
95
Eine enaktive Darstellung durch Häufigkeitstabellen kann diese Einsicht unterstützen. Vgl. Weustenfeld:
Augensummen zweier Würfel, S. 6.
92
23
Wenn mit einem Würfel geworfen wird, gibt es sechs Möglichkeiten. Dies gilt natürlich auch
für den zweiten Würfel, sodass 36 Möglichkeiten für das Werfen mit zwei Würfeln bestehen.
Der Fehler in Ω1 und Ω3 wird bei Betrachtung der möglichen Kombinationen der Tupel besonderes deutlich: Für das Tupel (5,5) müssen beispielsweise in Ω1 beide Würfel die 5 zeigen. Bei der (4,6) hingegen, kann der erste Würfel die 4, der zweite Würfel die 6 und umgekehrt zeigen. Dieser Sachverhalt wird in Ω2 durch die beiden Darstellungsmöglichkeiten
(4|6) und (6|4) symbolisiert. Die gleiche Argumentationsstruktur lässt sich auf Ω3 übertragen. In diesem Fall könnte die Augensumme 10 sogar durch (4|6), (6|4) und (5|5) dargestellt
werden. Daher ist das Laplace-Modell nur für Ω2 sinnvoll.96
Diese Einsicht kann vertieft werden, indem über die Laplace-Annahme bei einem gewöhnlichen Würfel diskutiert wird. Durch die Verarbeitung (Einmuldungen, Abrundungen der
Ecken) können Spielwürfel keine exakten Laplace-Würfel sein. Den Schülern wird klar, dass
es sich auch beim gewöhnlichen Würfel lediglich um ein mathematisches Modell handelt.97
Schon Laplace war bewusst, dass die Einschätzung der Gleichwahrscheinlichkeit „einer der
heikelsten Punkte in der Analyse des Zufallsgeschehens ist.“98
Nachdem die Schüler die Berechnung von Wahrscheinlichkeiten mit Hilfe des Zählprinzips
geübt haben (Bestimmung der restlichen Laplace-Wahrscheinlichkeiten beim Würfeln mit
zwei Würfeln in Aufgabenteil 2d), formulieren sie die Regel zur Berechnung von LaplaceWahrscheinlichkeiten. Laplace formulierte 1812 in seinem Werk „Théorie Analytique des
Probabilités“, in dem er den Wissenstand seiner Zeit über die Wahrscheinlichkeitsrechnung
zusammenfasste, ebenfalls diese Regel:
Wenn bei einem Zufallsexperiment mit endlicher Ergebnismenge alle möglichen Ergebnisse gleichbe|E|
rechtigt sind, dann wird die Wahrscheinlichkeit P(E) für das Ereignis E definiert durch P(E) ∶=
=
|Ω|
Anzahl der Elemente von E
Anzahl der Elemente von Ω
=
Günstige 99
.
Mögliche
An dieser Stelle wird zum ersten Mal auf den Arbeitsblättern der Begriff „Wahrscheinlichkeit“ (lat. probabilitas, engl. probability und franz. probabilité) durch das Symbol P bezeichnet. Außerdem wurde als Überschrift der Regel „so berechne ich Wahrscheinlichkeiten“ gewählt. Damit soll deutlich werden, dass es sich hierbei um keine Definition von „Wahrscheinlichkeit“ handelt. Den Begriff „Wahrscheinlichkeit“ mit Hilfe der Gleichwahrscheinlichkeit zu definieren, würde einen Zirkelschluss darstellen.100
96
Büchter; Henn: Elementare Stochastik, S. 169.
Bosch: Elementare Einführung, S. 14.
97
Büchter; Henn: Leitfaden Stochastik, S. 101.
98
Barth; Haller: Leistungskurs Stochastik, S. 76.
99
Büchter; Henn: Elementare Stochastik, S. 168.
100
Ebd. S. 167.
24
Durch Aufgabe 2 wird eine große Schwäche des Laplace-Ansatzes deutlich, da niemals bewiesen werden kann, dass dieses Modell Gültigkeit hat. Die Versuchsperson muss die Laplace-Annahme a priori treffen. Ist diese Annahme nicht korrekt, sind die errechneten Wahrscheinlichkeiten falsch. Den Schülern bleibt nur der Weg, die a priori getroffene Vermutung
mit Hilfe einer Versuchsreihe zu überprüfen (frequentistischen Wahrscheinlichkeitsbegriff).
In Aufgabe 3 beweisen die Schüler Eigenschaften von Laplace-Wahrscheinlichkeiten. Dies
ist ein wichtiger Schritt zum Verständnis des Wahrscheinlichkeitsbegriffs, da diese Eigenschaften in ähnlicher Form ebenfalls für die anderen Wahrscheinlichkeitsbegriffe gelten.
Damit kann später die Idee der Axiomatisierung der Wahrscheinlichkeitstheorie deutlich gemacht werden.101 Die Eigenschaften der Laplace-Wahrscheinlichkeit sind leicht aus dem
Merksatz der vorherigen Aufgabe 2 zu schließen. Die Schüler erlernen so symbolisch/ formal/ technisch mit Mathematik umzugehen:
Es liege ein Laplace-Experiment mit endlicher Ergebnismenge Ω = {ω1, ω2, . . . , ωn} vor. Dann gilt für
die Laplace-Wahrscheinlichkeiten der Ereignisse:
a) 0 ≤ P(E) ≤ 1 für alle E ⊆ Ω .
b) P(Ω) = 1; P(∅) = 0.
̅) = 1 − P(E) für alle E ⊆ Ω .
c) P(E
d) P(E1 ∪ E2) = P(E1) + P(E2) für alle E1, E2 ⊆ Ω mit E1∩E2 = ∅.
e) P(E1 ∪ E2) = P(E1) + P(E2) − P(E1∩E2) für alle E1, E2 ⊆ Ω .
f) Speziell gilt: P(E) = ∑ω∈E P({ω}) und P(Ω) = ∑ω∈Ω P({ω}) = ∑ni=1 P({ωi}) = 1.102
Die Schüler werden viele dieser Eigenschaften aus den bisherigen Aufgaben wiedererkennen. So spiegeln die Aussagen a), b) und d) die Eigenschaften Nichtnegativität, Normiertheit
und Additivität wider. Die Eigenschaft c) verwendeten die Schüler bei der Wette des Chevaliers.
In der Vertiefung lösen die Schüler ein weiteres historisches Problem, mit dem sich neben
de Méré, Pascal und Fermat auch Galileo Galilei auseinander gesetzt hat. Die Schüler widerlegen den Vorschlag de Mérés, dass die Wahrscheinlichkeiten für die Augensummen 11
bzw. 12 beim Werfen mit drei Würfeln gleichwahrscheinlich sind, indem sie an drei Beispielen mit Hilfe von Permutationen zeigen, dass die Elementarelemente nicht gleichwahrscheinlich sind. Die einzelnen Möglichkeiten zum Werfen einer 11 bzw. einer 12 wurden
den Schülern vorgegeben, um die Notwendigkeit der Gleichwahrscheinlichkeit der Elementarereignisse stärker hervorzuheben. Letztendlich berechnen sie die Laplace-Wahrschein27
25
lichkeiten P(Augensumme 11) = 216 und P(Augensumme 12) = 216.103
Eichler; Vogel: Leitfaden Stochastik, S. 102.
101
Bieler: Gesetze, S. 16.
102
Büchter; Henn: Elementare Stochastik, S. 168
103
Ebd. S. 77.
25
3.2.2 Arbeitsblatt II - Kombinatorischer Exkurs
Dieses Arbeitsblatt hat zum Ziel, die Berechnung von Wahrscheinlichkeiten im LaplaceGünstige
Modell durch das Zählprinzip Mögliche zu vertiefen. Dabei sollen die kombinatorischen Zählfiguren nicht vorgegeben, sondern zunächst entdeckt und anschließend Formeln für sie entwickelt werden. Dies bietet den Vorteil, dass die Schüler den Zählvorgang stärker reflektieren. Die Kombinatorik wird nur als Hilfsmittel zur Bestimmung von Laplace-Wahrscheinlichkeiten gesehen.104 Das Vorgehen zur Bestimmung der Laplace-Wahrscheinlichkeiten
mittels kombinatorischer Formeln verdeutlicht den Laplace-Wahrscheinlichkeitsbegriff, da
keine Alternativen zur berechneten Lösung vorhanden sind. Die Intuition bzw. die Hypothesen, die vor der Berechnung der Laplace-Wahrscheinlichkeit getroffen wurden, sind in diesem Modell nicht erwünscht bzw. nicht möglich. Damit geht der hypothetische Charakter
der Wahrscheinlichkeitsrechnung verloren.105 Die Schüler kennen allerdings schon Beispiele (Riemer-Quader/ die Wette des Chevaliers), in denen ein starres Beharren auf einer
theoretischen Annahme falsch sein kann. Dennoch sollen drei der vier Zählfiguren106 thematisiert werden, da sie den Vorteil der Laplace-Wahrscheinlichkeit (eine schnelle, theoretische Berechnung der Wahrscheinlichkeit a priori) verdeutlichen. Außerdem können aus
den Zählfiguren die verschiedenen diskreten Verteilungen herausgearbeitet werden.107
Aufgabe 1 des Arbeitsblattes beginnt mit einem offenen, enaktiven Einstieg in Form einer
Gruppenarbeit. Ein Vater hat zwei Freikarten gewonnen, die er unter seinen vier Kindern
aufteilen möchte.108 Dafür schreibt er die Namen seiner Kinder auf Zettel und legt sie in
einen Hut/ eine Urne. Die Aufgabe ist so gestellt, dass die drei kombinatorischen Grundfiguren und angewendet werden können: Erstens könnte der Vater den Namen eines Kindes
ziehen und diesen für die zweite Freikarte wieder zurück in die Urne legen, da in der Aufgabenstellung nicht festgelegt wurde, dass jedes Kind nur eine Karte erhalten darf. Zweitens
könnte der Vater für die erste Karte den Namen eines Kindes aus der Urne ziehen, das bei
der zweiten Freikarte nicht mehr an der Verlosung teilnimmt. Drittens könnte der Vater auch
mit einem Griff zwei Zettel aus der Urne ziehen.109
104
Sekretariat: Bildungsstandards im Fach Mathematik.
Riemer: Stochastische Probleme, S. 17.
106
Auf die Zählstrategie „Ziehen ohne Beachtung der Reihenfolge (Kombination) und mit Wiederholung“
wurde aus didaktischen Gründen verzichtet. Dies entspricht auch dem Vorgehen von Neue Wege. Wer diese
dennoch behandeln möchte, sei auf Büchter; Henn: Elementare Stochastik. verwiesen.
107
Auch wenn in dieser Arbeit nur die Binomialverteilung eine Rolle spielt, sollte den Schülern dennoch bewusst sein, dass es weitere Verteilungen gibt.
108
In den anderen Gruppen besitzt der Vater jeweils fünf Kinder und hat drei bzw. zwei Freikarten gewonnen.
109
Ähnliche Idee in Quinn; Wiest: Konstruktiver Zugang, S. 16. Die Problemsituation der Freikarten erscheint
allerdings realitätsnäher als das Tapezieren.
105
26
Dieser offene Weg wurde gewählt, da bereits vorhandene Formeln dazu führen, dass Schüler
bei Anwendungsaufgaben nicht wissen, welche Formel sie benutzen sollen. Durch diesen
Zugang wird das Verständnis für die jeweilige Zählfigur ins Zentrum gestellt. Daher wird
der argumentativen Begründung der Formel eine größere Bedeutung als der formalen Herleitung dieser beigemessen. Neben diesem inhaltlichen Aspekt bietet die Aufgabe den Schülern die Möglichkeit ihre Vorstellungen, zu mathematisieren. Bisher verwendeten sie die
Produktregel für die Kombinatorik in den Aufgaben intuitiv, in denen ein mehrstufiges Zufallsexperiment untersucht wurde (z. B. in der Wette des Chevaliers). Als kanonische Ergebnismenge kann in einem n-stufigen Zufallsexperiment grundsätzlich die Produktmenge Ω =
Ω1×Ω2×…×Ωn mit |Ω| = |Ω1| ∙ |Ω2| ∙…∙ |Ωn| verwendet werden. Die Wahrscheinlichkeitsverteilungen in den einzelnen Ωi, i ∈ {1,…, n}, induzieren eine Wahrscheinlichkeitsverteilung
auf Ω. Allerdings ist diese oft schwer zu berechnen, insbesondere wenn die einzelnen Zufallsexperimente voneinander abhängig sind. Um die Mengen zu analysieren, können die
Schüler sowohl das Baumdiagramm als auch das Urnenmodell heranziehen.110 Besonders
das Baumdiagramm hat den Vorteil, dass es sowohl dynamisch als auch statisch analysiert
werden kann.111 Schüler mit einem verstärkt funktionalen Denken werden die Entstehung
des Baumdiagramms als Prozess sehen, in dem sich das Zufallsexperiment von Knoten zu
Knoten entwickelt. Die Ergebnismenge kann mit {Ergebnis1,…, Ergebnism}n aufgefasst
werden. Die prädikativ denkenden Schüler werden das Baumdiagramm eher statisch interpretieren und die Ergebnismenge mit Ω ={(a1|a2|…|an) mit ai ∈ {Ereignis1,…, Ereignism}
mathematisch äquivalent beschreiben.112 Das Urnenmodell unterstützt tendenziell die prädikativ denkenden Schüler stärker.113 Im Folgenden wird anhand der Gruppe, in der der Vater
vier Kinder hat, die Aufgabe mit den beiden mathematischen Vorstellungen bearbeitet.
Ziehen mit Beachtung der Reihenfolge (Variation) und mit Zurücklegen
Das Baumdiagramm verdeutlicht einen zweistufigen Entscheidungsprozess.114 Auf jeder
Ebene des Baumes gibt es vier Möglichkeiten ein Kind auszuwählen. Dabei können die Namen der Kinder wiederholt auftreten. Daher ergeben sich 42 Möglichkeiten, die durch die
Anzahl der Äste dargestellt sind (Vgl. Abbildung 3). Jeder Ast entspricht eindeutig einem 2Tupel.
110
Beide Werkzeuge idealisieren Zufallsvorgänge. Vgl. Zufall und Gesetz S. 29.
Engel: Stochastik, S. 21.
111
Steinbring: Entwicklung des Wahrscheinlichkeitsbegriffs, S. 104.
Eichler; Vogel: Leitfaden Stochastik, S. 129.
112
Büchter; Henn: Elementare Stochastik, S. 209.
Dreher: Baumdiagramme, S. 59.
113
Gallin: Prädikatives und funktionales Denken, S.11.
114
Dreher: Baumdiagramme, S. 57.
27
Abbildung 3: Baumdiagramm Zählfigur I.
Quelle: Eigene Konzeption.
Im Urnenmodell befinden sich die Zettel mit den Namen der Kinder. Es werden zwei Zettel
gezogen, die wieder in die Urne zurückgelegt werden. Außerdem wird der Name notiert,
sodass die Reihenfolge der Ziehungen berücksichtigt wird. So entsteht ein geordnetes 2Tupel, das Elemente (Namen) mehrfach enthalten kann. So gibt es insgesamt 42 Möglichkeiten. Mit Hilfe der anderen Gruppen kann diese Erkenntnis zu der Formel nk verallgemeinert werden.115
Ziehen mit Beachtung der Reihenfolge (Variation) und ohne Zurücklegen
Das Baumdiagramm drückt wieder den Entscheidungsprozess aus, bei dem sich auf jeder
Ebene die Anzahl der Entscheidungsmöglichkeiten um 1 verringert. Somit gibt es zunächst
vier Entscheidungsmöglichkeiten und im zweiten Versuch lediglich drei. Daran wird die
Abhängigkeit der zweiten Ziehung von der ersten deutlich. Die Schüler müssen das Modell
also an die Situation anpassen.116 Damit gibt es nur noch 12 Möglichkeiten (Vgl. Abbildung
4). Wiederum entspricht jeder 2-Variation eindeutig einem 2-Tupel.
Abbildung 4: Baumdiagramm Zählfigur II.
Quelle: Eigene Konzeption.
In einer Urne befinden sich die Namen der vier Kinder. Nachfolgend wird ein Name gezogen, der nicht mehr in die Urne zurückgelegt wird. Die Zettel werden nun der Reihe nach
notiert, sodass ein geordnetes 2-Tupel entsteht, indem jedes Element nur einmal vorkommt.
Mit Hilfe der anderen Gruppen erschließen sich die Schüler so die Formel n∙(n-1)∙(n-2)∙…∙
115
116
Kütting; Sauer; Padberg: Elementare Stochastik, S. 135.
Dreher: Baumdiagramme, S. 68.
28
(n-k+1) =
n!
.
(n−k)!
Dabei muss die Lehrkraft das Symbol n! = n∙(n-1)∙(n-2)∙…∙1 als Fakultät
einführen.117
Ziehen ohne Beachtung der Reihenfolge (Kombination) und ohne Zurücklegen
Bei dieser Art der Zählstrategie ist es nur bedingt günstig, sich den Baum als Entscheidungsprozess vorzustellen, da sonst der Eindruck entstehen könnte, dass die Reihenfolge beachtet
wird. Allerdings kann der Baum aus dem Zählsystem „Ziehen mit Beachtung der Reihenfolge (Variation) und ohne Zurücklegen“ als Grundlage fungieren. Jedoch spielt in diesem
Fall die Reihenfolge keine Rolle, sodass die identischen Äste herausgerechnet werden müssen (gestrichelte Äste). Es bleibt ein Baum übrig, der das Ziehen ohne Beachtung der Reihenfolge und ohne Zurücklegen darstellt (vgl. Abbildung 5). Dieser Darstellungswechsel
zeigt den Schülern, wie sich das Modell des Baumdiagramms verändert, wenn die Situation
leicht verändert wird.118
Abbildung 5: Baumdiagramm Zählfigur III.
Quelle: Eigene Konzeption.
Im Urnenmodell werden die vier Namen der Kinder ohne Zurücklegen und ohne Beachtung
der Reihenfolge gezogen und als Anhäufung gesammelt. Daher ist die Vorstellung eines
Ziehens mit einem Griff sinnvoll. Damit muss die Anzahl der Namen größer als die Anzahl
der Freikarten sein (Die gezogenen Namen sind eine Teilmenge der möglichen Namen).
In diesem Fall müssen die Gruppen zusammenarbeiten, um eine Formel zu entdecken. Erst
in der Gruppe, in der es fünf Kinder und drei Freikarten gibt, wird ersichtlich, dass durch k!
geteilt werden muss und nicht durch k. Diese Fehlvorstellung ist besonders für die Gruppen
mit zwei Freikarten möglich, da 2! = 2. Es lassen sich also die Möglichkeiten einer k-Kombination ohne Wiederholung berechnen, indem zunächst alle k-Variationen ohne Wiederholung berechnet und anschließend durch die Anzahl der k-Permutationen dividiert werden.
n!
Schließlich lässt sich also die Formel k!∙(n−k)! ∶= (nk) ermitteln.119
117
Kütting; Sauer; Padberg: Elementare Stochastik, S. 135.
Dreher: Baumdiagramme, S. 62.
119
An dieser Stelle kann der Binomialkoeffizient beispielsweise mit dem Pascal’schen Dreieck verknüpft und
vertieft werden. Althoff: Wieviel Kombinatorik, S. 5.
118
29
In Aufgabe 2 sollen die erarbeiteten kombinatorischen Grundfiguren vertieft werden. Nachdem in Aufgabe 1 alle drei Zählfiguren in einer Aufgabe möglich waren, soll nun zu jeder
Figur eine typische Situation vorgestellt werden.120 Die Repräsentanten wurden jeweils aus
dem Bereich des Glücksspiels entnommen und sollen im Folgenden eine wichtige Gedankenstütze für die Schüler beim Lösen kombinatorischer Aufgaben darstellen.121 Das erste
Beispiel beinhaltet eine Fußballwette: Zunächst muss auf elf Ergebnisse von Spielen (Sieg
Heimteam, Unentschieden oder Sieg Auswärtsteam) gewettet werden. Dieses Beispiel spiegelt das Modell „Ziehen mit Beachtung der Reihenfolge (Variation) und mit Zurücklegen“
wider, da es einerseits drei Möglichkeiten gibt, den Schein auszufüllen und andererseits die
Reihenfolge wichtig ist, weil nur so eine Zuordnung der ausgewählten Spiele erfolgen kann.
Die Schüler können daher die Anzahl der Möglichkeiten mit 311 = 177.147 angeben.122
Für das Modell „Ziehen mit Beachtung der Reihenfolge (Variation) und ohne Zurücklegen“
ist das Pferderennen beispielhaft. Hierbei ist die Reihenfolge des Ankreuzens (obere, mittlere und untere Zeile) wichtig, da der Platz des Pferdes (1., 2. und 3.) vorausgesagt werden
soll. Da außerdem auf kein Pferd doppelt gewettet werden kann, veranschaulicht dies das
Ziehen ohne Zurücklegen. Insgesamt können die Möglichkeiten mit der Formel
15!
(15−3)!
n!
(n−k)!
=
= 15∙14∙13 = 2.730 berechnet werden.123
Das letzte Modell „Ziehen ohne Beachtung der Reihenfolge (Kombination) und ohne Zurücklegen“ wird durch das Lotto-Modell repräsentiert. Aus 49 Kugeln sollen sechs gezogen
werden. Da die Kugeln immer der Größe nach geordnet werden (vgl. Fernsehdarstellung),
bleibt die Reihenfolge unbeachtet. Genauso gut könnten beim Lotto mit einem Zug sechs
Kugeln herausgenommen und notiert werden. Dadurch wird deutlich, dass nach dem Prinzip
„ohne Zurücklegen“ gezogen wird. Es gibt also (49
) = 13.983.816 Möglichkeiten den Schein
6
auszufüllen.124
In Aufgabe 2b) wird eine Verbindung von der Kombinatorik zum Laplace-Wahrscheinlichkeitsbegriff gezogen. Hieran soll deutlich werden, dass die Kombinatorik lediglich als Hilfsmittel zur Bestimmung von Wahrscheinlichkeiten genutzt wird. Dafür wurden die verschiedenen Gewinnmöglichkeiten in der vorgestellten Beispiele (Fußball-Toto, Pferderennen,
120
Je nach Klassenstärke können sich die Schüler die typische Situation selbst ausdenken und diese an die
Formel anpassen (Prinzip der Reversibilität).
121
Ein Argumentieren von idealen Situationen schlug Arthur Engel bereist 1973 vor. Vgl. Engel: Wahrscheinlichkeitsrechnung und Statistik.
122
Büchter; Henn: Elementare Stochastik, S. 231.
123
Ebd. S. 233.
124
Mittag: Statistik, S. 180.
30
Lotto) möglichst realitätsnah formuliert. Die Schüler müssen die Formel
Günstige
Mögliche
anwen-
den, um die jeweiligen Gewinnkategorien zu bestimmen.
Nachdem in Aufgabenteil 2a) schon der Nenner mit 311 = 177.147 für das Fußball-Toto bestimmt wurde, erkennen die Schüler, dass zur Gewinnklasse I genau eine dieser 177.147
1
Möglichkeiten gehört. Die Laplace-Wahrscheinlichkeit berechnet sich daher auf 177147. In
der Gewinnklasse II müssen zehn Spiele richtig getippt werden, sodass eines der elf Spiele
falsch getippt werden kann. Da es in jeder dieser Spiele zwei mögliche falsche Antworten
gibt (z. B. können beim richtigen Tipp „Sieg Heimmannschaft“, die Fehltipps „Unentschieden“ oder „Sieg Auswärtsteam“ abgegeben werden), besitzen die Spieler 22 günstige Mög22
lichkeiten. Daher berechnet sich die Laplace-Wahrscheinlichkeit auf 177147. Für die Gewinnklasse III benötigen die Spieler neun richtige Tipps. Es dürfen also zwei Spiele falsch getippt
werden. Der Zähler kann im Zählsystem „Ziehen ohne Beachtung der Reihenfolge (Kombination) und ohne Zurücklegen“ mit Hilfe des Binomialkoeffizienten (11
) ausgerechnet wer2
den. Genauso gut könnten die Schüler Zählstrategien anwendenden und erkennen, dass es
für das erste falsch getippte Spiel elf, für das zweite nur noch zehn Möglichkeiten gibt. Allerdings fallen noch die identischen Möglichkeiten (identische Pfade in der Vorstellung des
Baumdiagramms) heraus. Diese Überlegungen führen ebenfalls zur kombinatorischen
Grundfigur (11
) (Diese Überlegungen wurden bereits in Aufgabe 1 „Zählverfahren“ ange2
wendet). Da es außerdem bei jedem falschen Tipp zwei Möglichkeiten gibt, also 2∙2 = 4,
(11) ∙ 4
220
2
berechnet sich die Laplace-Wahrscheinlichkeit auf 177147
= 177147.125
Des Weiteren berechnen die Schüler beim Pferderennen die möglichen Wege zum Ausfüllen
15!
des Gewinnzettels mit (15−3)! = 2.730. Da in der Gewinnklasse I die drei Gewinnerpferde in
der richtigen Reihenfolge getippt werden müssen, gibt es nur eine günstige Möglichkeit zu
1
gewinnen. Demnach beträgt die Laplace-Wahrscheinlichkeit 2730. Für die Gewinnklasse II
müssen die Permutationen der drei Gewinnerpferde betrachtet werden, das heißt es gibt 3!=6
Möglichkeiten. Da eine dieser sechs Möglichkeiten zu Gewinnkategorie I gehört, bleiben
fünf günstige Möglichkeiten für die Gewinnkategorie II. Die Laplace-Wahrscheinlichkeit
5
ergibt deshalb 2730.126
125
126
Büchter; Henn: Elementare Stochastik, S. 232.
Ebd. S. 233.
31
Darüber hinaus wurden für das Lotto-Spiel ohne die Zusatzzahl (49
) = 13.983.816 Möglich6
1
keiten berechnet. Damit beträgt die Laplace-Wahrscheinlichkeit 13983816 für sechs Richtige
(ohne Zusatzzahl). Für drei Richtige müssen ergeben sich demnach (63) Möglichkeiten. Die
restlichen drei getippten Zahlen sind also unter den verbliebenen 43 Zahlen, sodass es dafür
(43
) Möglichkeiten gibt. Insgesamt berechnet sich die Laplace-Wahrscheinlichkeit für drei
3
Richtige daher auf
(63) ∙ (43
3)
(49
6)
vier bzw. fünf Richtige zu
246820
= 13983816. Analog berechnen sich die Wahrscheinlichkeiten für
(64) ∙ (43
2)
(49
6)
=
13545
bzw.
13983816
(65) ∙ (43
1)
(49
6)
=
258
.127 Natürlich kann in
13983816
diese Überlegungen noch die Superzahl und die Zusatzzahl eingebaut werden. Besonders
bei der Berechnung der Laplace-Wahrscheinlichkeit unter Berücksichtigung der Zusatzzahl
taucht ein weiteres Problem auf, da die gezogenen Kugeln nicht mit der Anzahl der getippten
Kugeln übereinstimmen. Die Schüler können zur Lösung zwei Perspektiven einnehmen: In
der ersten Perspektive können sie das Problem aus der Sicht der getippten Zahlen betrachten.
Für die Gewinnklasse „4 Richtige mit Zusatzzahl“ ergeben sich damit folgende Überlegungen: Der Anzahl der Möglichkeiten den Tippzettel auszufüllen bleibt mit (49
) = 13.983.816
6
gleich. Für den Zähler müssen vier der sechs getippten Kugeln Gewinnzahlen sein, das heißt
(64). Außerdem muss eine Kugel der Zusatzzahl entsprechen, dafür gibt es (11) Möglichkeiten. Die letzte getippte Zahl ist also unter den verbliebenen 42 Zahlen. Somit ergibt sich der
Term
(64) ∙ (11) ∙ (42
1)
(49
6)
630
= 13983816 = 0,000045. Hinter der zweiten Variante verbirgt sich die Per-
spektive der gezogenen Zahlen. Damit erhöht sich die Ergebnismenge auf (49
) ∙ 43. Dies
6
liegt in der Vorstellung begründet, dass zuerst sechs Kugeln ohne Beachtung der Reihenfolge und ohne Zurücklegen gezogen werden und danach eine weitere aus den verbliebenen
43. Aus dieser Perspektive wandelt sich der Zähler ebenfalls. Wieder müssen vier der sechs
getippten Zahlen gezogen werden. Die zwei restlichen gezogenen Zahlen befinden sich unter
den 43 nicht angekreuzten Zahlen und die Zusatzzahl muss unter den beiden verbliebenen
getippten Zahlen sein. Dies führt zum Bruch
2
(64) ∙ (43
2 ) ∙ (1)
(49
6 )∙ 43
=
27090
601304088
= 0,000045. Die Be-
rechnungen zu den restlichen Gewinnklassen mit Berücksichtigung der Zusatzzahl laufen
analog.128
127
128
Basler: Aufgabensammlung, S. 35.
Büchter; Henn: Elementare Stochastik, S. 235.
32
Darüber hinaus hat Aufgabe 2c) das Ziel den Laplace-Wahrscheinlichkeitsbegriff erneut zu
reflektieren. Oftmals ist eine Gleichwahrscheinlichkeit der Elementarereignisse vollkommen unrealistisch.129 Sowohl beim Fußball-Toto als auch beim Pferderennen sind die Teams
bzw. Pferde nicht gleich stark. Außerdem wird jeder Spieler die einzelnen Mannschaften
bzw. Pferde individuell einschätzen (subjektiver Wahrscheinlichkeitsbegriff). Neben diesen
Einwänden können auch statistische Argumente angeführt werden, um zu zeigen, dass das
Laplace-Modell für diese Situationen nicht angemessen ist. Beispielsweise gewinnt die
Heimmannschaft tendenziell öfter beim Fußballspiel. Lediglich für das Lotto-Spielen ist das
Laplace-Modell sinnvoll. Zwar können auch hier subjektive Wahrscheinlichkeiten (Glückszahlen oder Ähnliches) eine Rolle spielen, aber die bisherigen Ziehungen der Lottozahlen
zeigen, dass jede Zahl ungefähr gleich wahrscheinlich ist. Die kombinatorischen Formeln
spiegeln also nicht die Realität wider, sondern sind ein Mittel, um aus Hypothesen einfachere
Hypothesen zu gewinnen.130 Den Schülern wird erneut bewusst, dass die Laplace-Wahrscheinlichkeiten nicht bewiesen, sondern lediglich mit Hilfe des frequentistischen Wahrscheinlichkeitsbegriffs überprüft werden können.131
Die dritte Aufgabe behandelt das historische Problem des Teilungsproblems. In diesem muss
ein Spiel zwischen gleich starken Spieler beim Stand von 4:3 im Spielmodus „Best of 9“
abgebrochen werden. Ebenso wie die Mathematiker in der Geschichte werden die Schüler
hier plausible Argumente haben, wie die Einsätze aufgeteilt werden sollen.132 Neben den
Möglichkeiten „der Führende bekommt alles“ und „der Einsatz wird jedem Spieler zurückgegeben“, gibt es auch die Möglichkeit, den Einsatz gemäß dem Spielverhältnis im Verhältnis 4:3 aufzuteilen. Diese Idee hatte auch Luca Pacioli. Ihm widersprach Niccolò Tartaglia,
der das Ende das Spiel mit einbezog und daher den Pot im Verhältnis (5+4-3):(5+3-4), also
3:2 aufteilen wollte. Eine weitere Lösung lieferten Pascal und Fermat. Statt den Fokus auf
die bisher gespielten Spiele zu legen, betrachteten sie die zukünftigen Spiele. Damit verwendeten sie als erstes wahrscheinlichkeitstheoretische Annahmen:133
„Pascals Lösung ist nun die folgende: Wenn B die nächste Partie gewinnen würde, wäre Gleichstand,
1
und B müsste die Hälfte des Einsatzes bekommen. Da die Chance zu gewinnen nur ist, gebührt ihm
1
2
die Hälfte der Hälfte, also der Einsätze, d. h. es ist im Verhältnis 3:1 zu teilen.“134
4
129
Lehn; Roes: Probleme in Aufgabenstellungen, S.30.
Riemer: Stochastische Probleme, S. 33.
131
Büchter; Henn: Elementare Stochastik, S. 232.
132
Eine schöne Darstellung des Problems findet sich in Devlin: Pascal, Fermat. In diesem wird an Hand des
Briefwechsels von Fermat und Pascal eine „Reise in die Geschichte der Mathematik“ unternommen.
133
Wirths: Geburt der Stochastik, S. 10.
134
Kütting; Sauer; Padberg: Elementare Stochastik, S. 79.
130
33
Fermat hingegen verwendet das Zählprinzip, um die Aufgabe zu lösen. Sowohl das Urnenmodell als auch das Baumdiagramm sind geeignet, um diese Aufgabe zu veranschaulichen.
Da das Spiel nach spätestens zwei Partien beendet ist, gibt es vier mögliche Tupel des Spielverlaufs: (A,A), (A,B), (B,B), (B,A).135 Von diesen Spielverläufen sind drei günstig für A
und nur einer für B. Daher sollte im Verhältnis 3:1 geteilt werden. Dies wird auch am folgenden Baumdiagramm deutlich (Vgl. Abbildung 6).
Abbildung 6: Baumdiagramm Teilungsproblem (kombinatorisch).
Sieg A
Sieg A
Sieg B
Sieg B
Sieg A
Sieg A
Sieg A
Sieg B
Sieg A
Sieg B
Quelle: Eigene Konzeption.
Beim Teilungsproblem handelt es sich um eine normative Frage. Alle genannten Vorschläge
sind weder richtig noch falsch. Vielmehr geht es darum, welcher dieser Vorschläge die Realität am besten repräsentiert. Durch Simulationen wird deutlich, dass der Weg von Pascal/
Fermat der realitätsnaheste ist. Ihre Methode den künftigen Spielverlauf in den Blick zu
nehmen, konnte auf viele stochastische Fragestellungen übertragen werden, sodass sich die
Disziplin stark weiterentwickelte.136 Außerdem bietet die Lösung Fermats die Möglichkeit
die Pfad- und die Summenregel zu thematisieren. Zuvor wurden diese nur intuitiv verwendet. Diese Regeln haben den großen Vorteil, dass die Schüler nicht mehr die Ereignismengen
und kombinatorischen Überlegungen aufstellen müssen, bevor sie Wahrscheinlichkeiten berechnen können. Besonders deutlich werden die Regeln bei der Betrachtung eines analogen
Baumdiagramms für das Teilungsproblem (vgl. Abbildung 7):137
Abbildung 7: Baumdiagramm Teilungsproblem (verkürzt).
1
2
1
2
Sieg A
1
2
Sieg A
1
2
Sieg B
Quelle: Eigene Konzeption.
135
Freudenthal: Mathematik als pädagogische Aufgabe, S. 529.
Kütting; Sauer; Padberg: Elementare Stochastik, S. 79.
137
Ebd. S. 80.
136
34
Das Baumdiagramm ähnelt dem kombinatorischen Baumdiagramm aus Abbildung 6. Allerdings sind nicht alle Äste abgebildet, was das Berechnen von Wahrscheinlichkeiten erleichtert. Aufgabe 3c) verdeutlicht dieses Prinzip. Dort sollen die Schüler entscheiden, ob sie aus
einer Urne mit 10 Losen (ein Gewinnlos) anfangen wollen zu ziehen. Es reicht durch die
Pfadregeln aus, die Ergebnismenge mit {(Gewinn, Niete)}10 darzustellen. Dabei ist das Laplace-Modell nicht mehr sinnvoll, da die Elementarereignisse nicht gleichwahrscheinlich
sind. Um das Laplace-Modell weiter zu erhalten, müssten die Schüler die Nieten künstlich
unterscheidbar machen. Dieses Prinzip wendeten sie bereits in der Aufgabe „Werfen mit
zwei Würfeln“ auf dem Arbeitsblatt „Der Laplace-Wahrscheinlichkeitsbegriff I“ an. Allerdings ist dieses Vorgehen für die Schüler nicht intuitiv. Statt das Baumdiagramms komplett
auszuschreiben, damit alle Pfade gleichwahrscheinlich sind, können die Schüler die Pfade
mit den Wahrscheinlichkeiten beschriften. Beides führt zum gleichen Ergebnis. Im künstlich
erweiterten Laplace-Ansatz würden die Schüler alle 10! = 36.288.000 Pfade des Baumdiagramms hinschreiben und die günstigen Wege abzählen. Sie würden für beide Spieler auf
1.814.400 Pfade kommen. So wird ersichtlich, dass es gleichgültig ist, welcher Spieler beginnt. Durch die Verwendung der Pfadregeln geht dies schneller. Die Gewinnwahrschein1
9
8
1
9
8
7
6
5
4
3
2
1
lichkeit des ersten Spielers beträgt 10 + 10 ∙ 9 ∙ 8 +…+ 10 ∙ 9 ∙ 8 ∙ 7 ∙ 6 ∙ 5 ∙ 4 ∙ 3 ∙ 2, wobei jeder
der fünf Summanden gekürzt
1
10
beträgt. Eine analoge Rechnung ergibt, dass die Gewinn1
wahrscheinlichkeit für den zweiten Spieler ebenfalls 10 für jeden der fünf Summanden beträgt.
Im zweiten Beispiel der Aufgabe 3c) wird die Aufgabenstellung leicht variiert, da nun ein
Glücksrad abwechselnd gedreht wird (Das Gewinnfeld hat die Laplace-Wahrscheinlichkeit
1
). Es wird wieder die Frage gestellt, ob man anfangen will zu drehen. Damit befinden sich
10
die Schüler in der Zählstrategie „Ziehen mit Beachtung der Reihenfolge und ohne Zurücklegen“. Die Variation in der Aufgabenstellung führt letztendlich dazu, dass zwischen abhängigen und unabhängigen Zufallsexperimenten unterschieden wird. Mit Hilfe der Pfadregeln
1
1
3
berechnet sich beim ersten Spieler die Wahrscheinlichkeit zu gewinnen auf 4 + (4)2 ∙ 4 +…=
1
3
n+1
∑∞
∙ (4)n. Für den zweiten Spieler ergibt sich
n=0 (4)
3
3
1
1
4
∙
3
4
1
3
1
n+1
+ (4)2 ∙ (4)2 +…= ∑∞
∙
n=0 (4)
3
n+1
(4)n+1 = 4 ∙ ∑∞
∙ (4)n. Ein Vergleich der einzelnen Summanden zeigt, dass es günstin=0 (4)
ger ist, als Erstes am Glücksrad zu drehen.138 Durch den theoretisch abzählbar unendlich
138
Strick: Vorstellungen, S. 5.
Walter: Heuristische Strategien, S. 14.
35
langen Spielverlauf wird auch die Ergebnismenge unendlich groß. Hier ist das Abzählverfahren über das Baumdiagramm nicht möglich und führt zur Fragestellung, ob ein LaplaceAnsatz bei einer (abzählbar) unendlich großen Ergebnismenge überhaupt realisierbar ist. Auf
dem nächsten Arbeitsblatt (Laplace-Wahrscheinlichkeitsbegriff III) werden die Schüler
diese Frage beantworten und erkennen, dass das Laplace-Modell in diesem Fall zu einem
Widerspruch führt.139
Das Arbeitsblatt „Der Laplace-Wahrscheinlichkeitsbegriff II“ endet mit der Formulierung
der Pfad- und Summenregel:
(1)Pfadmultiplikationsregel: Die Wahrscheinlichkeit für einen Pfad ist gleich dem Produkt der Wahrscheinlichkeit entlang dieses Pfads.
(2)Pfadadditionsregel: Die Wahrscheinlichkeit für ein Ereignis ist gleich der Summe der Wahrscheinlichkeiten aller Pfade, die zu diesem Ereignis gehören. 140
Diese Pfadregeln werden im Bereich der bedingten Wahrscheinlichkeit wieder aufgegriffen
und begründet. An dieser Stelle sollen die intuitiven Vorstellungen der Schüler festgehalten
werden. Daher fehlt die dritte Pfadregel, die meistens unter dem Satz von Bayes bekannt ist.
3.2.3 Arbeitsblatt III - Kontinuierliche Ergebnismengen
Die erste Aufgabe des Arbeitsblattes „Der Laplace-Wahrscheinlichkeitsbegriff III“ greift
das Glücksrad aus der letzten Stunde erneut auf. Die Aufgabe beginnt mit der Berechnung
einer Laplace-Wahrscheinlichkeit des Glücksrades. Durch eine Variation in der Aufgabenstellung werden zwei mögliche Schwächen des Laplace-Ansatzes deutlich gemacht. In der
ersten wird der Laplace-Ansatz für unendlich abzählbare Ergebnismengen diskutiert, indem
die einzelnen Sektoren des Glücksrades unendlich klein werden. Diese Fragestellung wurde
schon in Aufgabe 3 des letzten Arbeitsblattes angedeutet, da das Abzählen im unendlich
langen Baumdiagramm unmöglich erschien. Die Problemstellung wird in Aufgabe 1 leicht
variiert, indem die abzählbar unendliche Ergebnismenge nicht prozesshaft entsteht, sondern
durch abzählbar unendlich viele Elementarereignisse dargestellt wird. Da alle Elementarereignisse die gleiche Wahrscheinlichkeit p > 0 haben, muss jedes Ereignis, das aus mehr als
1
n > p Ergebnissen besteht, eine Wahrscheinlichkeit von > 1 besitzen. Dies ist allerdings auf
Grund der Eigenschaften der Wahrscheinlichten nicht möglich. Um diesem Widerspruch zu
entgehen, müssen also alle Elementarereignisse die Wahrscheinlichkeit 0 besitzen. Diese
Lakoma: Lokale Modelle, S. 10.
139
Engel: Wahrscheinlichkeitsrechnung und Statistik, S. 25.
140
Büchter; Henn: Elementare Stochastik, S. 216.
Haftendorn: Mathematik sehen und verstehen, S. 266.
Engel: Wahrscheinlichkeitsrechnung der Statistik, S. 16.
36
1
Idee würde zu der in der Analysis entwickelten Vorstellung „ = 0“ passen. Allerdings führt
∞
diese ebenfalls in einer abzählbar unendlichen Menge zum Widerspruch, da P(Ω) = 0+0+…=
0 ≠ 1. Die Berechnung von Laplace-Wahrscheinlichkeiten ist also in abzählbar unendlichen
Mengen nicht möglich. Jedoch können durch die Aufgabe der Gleichwahrscheinlichkeitsannahme Wahrscheinlichkeiten auch in abzählbar unendlichen Mengen berechnet werden.
Die zweite Variation (Wie kann ich Wahrscheinlichkeiten berechnen, wenn die Felder nicht
gleich groß sind?), destruiert daher den Ansatz der Gleichwahrscheinlichkeit. Die Schüler
können nicht mehr die einzelnen Felder abzählen, sondern müssen auf die Geometrie zurückgreifen. Durch diesen Rückbezug wird der endliche Wahrscheinlichkeitsraum zum ersten Mal verlassen. An dieser Stelle treffen die Schüler auf kontinuierliche Wahrscheinlichkeitsräume, die bei der Untersuchung des axiomatischen Wahrscheinlichkeitsbegriffs genauer thematisiert werden. Außerdem kann bei der Berechnung von stetigen Wahrscheinlichkeitsverteilungen (z. B. die Normalverteilung) über das Integral der Dichtefunktion auf
dieses Beispiel verwiesen werden.141
Die Schüler versuchen durch geometrische Überlegungen, einen Laplace-ähnlichen Zustand
herzustellen, um die Wahrscheinlichkeiten analog berechnen zu können.142 Gleichzeitig tritt
dadurch der Modellierungsaspekt in den Vordergrund. Die Aufgabe kann durch die Betrachtung der Winkel oder der Flächen gelöst werden. Ersteres betrachtet das Glücksrad als einen
Kreis mit 360 gleich großen Winkeln. Damit bleibt ein diskretes Modell die Grundlage. Dies
ist allerdings nicht möglich, da hier vernachlässigt wird, dass die Einteilung der Winkel viel
feiner (kontinuierlich) erfolgen könnte. Somit muss dieses Modell muss verworfen werden,
da im ersten Teil der Aufgabe gezeigt wurde, dass der Laplace-Ansatz bei unendlichen Mengen nicht möglich ist.143
Die zweite Möglichkeit besteht darin, die Fläche bzw. das Bogenmaß des Gewinnfeldes zu
betrachten. Dabei kann jede Zahl zwischen [0; πr2] bzw. [0; 2πr[ vorkommen. Die Ergebnismenge ist also überabzählbar. Mit dieser Modellierung wurde also ein kontinuierlicher
Wahrscheinlichkeitsraum gewählt. Wenn jeder Punkt dieses Kontinuums gleichwahrscheinlich ist, kann über die Fläche bzw. das Bogenmaß die Wahrscheinlichkeit wie im LaplaceAnsatz berechnet werden:
Maßzahl des Flächeninhalts des Gewinnfeldes
Maßzahl des Flächeninhalts des Glückrades
=
Maßzahl der Bogenlänge des Gewinnfeldes
Maßzahl der Bogenlänge des Glückrades
α
= 2π 144.
141
Kütting; Sauer; Padberg: Elementare Stochastik, S. 120.
Kütting: Didaktik der Stochastik, S.51.
143
Dies berücksichtigt beispielsweise Kütting; Sauer; Padberg: Elementare Stochastik, S. 121 nicht.
144
Der Winkel α gibt die Winkelgröße des Gewinnfeldes an.
142
37
Mit Hilfe des geometrischen Wahrscheinlichkeitsbegriffs können also mit einer Laplaceähnlichen Methode Wahrscheinlichkeiten berechnet werden. Auf diese Weise können die
Schüler Wahrscheinlichkeiten für Teilintervalle von Ω berechnen. Allerdings bleibt für einelementige Mengen die Problematik, dass ihr die Wahrscheinlichkeit 0 zugewiesen werden
muss. Eine Wahrscheinlichkeit 0 bedeutet daher nicht, dass das Ereignis unmöglich ist, sondern nur, dass es sehr unwahrscheinlich ist. Dies widerspricht wie so oft bei (überabzählbar)
unendlichen Mengen (z.B. Hilbert-Hotel) unserer Intuition.145 Die Schüler erkennen, dass es
Konsequenzen hat, ob die Ergebnismenge endlich, abzählbar oder überabzählbar unendlich
ist. Dies erklärt zum einen den Aufbau der Axiomatik und zum anderen sensibilisiert es die
Schüler, bei Mengenveränderungen vorsichtig zu sein.146
In der zweiten Aufgabe wird der erste Teil des Arbeitsblattes „Sind wir gute Statistiker?“
behandelt.147 Die Schüler sollen selbstständig ihre intuitiven Vorhersagen mit Hilfe des Laplace-Wahrscheinlichkeitsbegriffs überprüfen. Die Aufgabe wird durch einen kurzen Informationstext über die Arbeiten von Kahneman und Tversky, von denen ein Großteil der Aufgaben stammt, abgerundet. Außerdem wird eine Literaturempfehlung für die Schüler gegeben, die sich für dieses Thema besonders interessieren.
Die Behandlung des Laplace-Wahrscheinlichkeitsbegriffs soll durch Aufgabe 3 abgeschlossen werden. Hierbei zeigen zwei Zitate (Pascal und Bernoulli), welche Stärken und Schwächen der Laplace-Wahrscheinlichkeitsbegriff besitzt. In der Aussage Pascals „Je vois bien,
que la verité est la même à Toulouse et à Paris“ wird das Selbstverständnis der Deterministen
aus dieser Zeit deutlich: Die Stochastik bringt keinerlei Unsicherheit mit sich, sodass die
„Wahrheit“ durch sie ermittelt werden kann. Somit besitzt die Wahrscheinlichkeit keinen
hypothetischen Charakter. Ebenso reichen theoretische Überlegungen vor dem Experiment
aus, um das richtige Ergebnis zu ermitteln, sodass eine Revision des Ergebnisses nicht notwendig ist. Eine Versuchsdurchführung ist daher nicht erforderlich, falls die richtige Ergebnismenge gewählt wird. Dieses Verständnis änderte sich durch eine verstärkte Auseinandersetzung mit der Statistik. Viele Ereignisse konnten im Gegensatz zum Glückspiel nicht mehr
als gleichwahrscheinlich angenommen werden. Diese Schwäche betont das Zitat Bernoullis,
was den Übergang zum frequentistischen Wahrscheinlichkeitsbegriff bildet:
„Welcher Sterbliche könnte aber je die Anzahl der der Krankheiten, welche den menschlichen Körper
an allen seinen Teilen und in jedem Alter befallen und den Tod herbei-führen können, ermitteln und
angeben, um wie viel leichter diese als jene Krankheit, die Pest als die Wassersucht, die Wassersucht
145
Kütting; Sauer; Padberg: Elementare Stochastik, S. 121.
Barth: Leistungskurs, S. 111.
147
Die Aufgaben wurden im Kapitel „Sind Menschen gute Statistiker“ vorgestellt bzw. können mit den erlernten Kenntnissen bearbeitet werden. Daher werden sie an dieser Stelle nicht ausführlich beschreiben.
146
38
als Fieber den Mengen zugrunde richtet, um daraus eine Vermutung über das Verhältnis von Leben und
Sterben künftiger Generationen abzuleiten.“148
In der Vertiefung recherchieren die Schüler die Eigenschaften der relativen Häufigkeiten aus
der Sek. I, welche die Grundlage für den frequentistischen Wahrscheinlichkeitsbegriff darstellen. Dabei erkennen sie, dass diese Eigenschaften sehr ähnlich zu denen des LaplaceModells sind. Insbesondere tauchen die Eigenschaften der Nichtnegativität, Normiertheit
und Additivität erneut auf.149
3.3 Der frequentistische Wahrscheinlichkeitsbegriff
3.3.1 Arbeitsblatt I - Das empirische Gesetz der großen Zahlen
Auch bei der Erkundung des frequentistischen Wahrscheinlichkeitsbegriffs dienen die Intuitionen der Schüler als Grundlage. Daher beginnt die erste Aufgabe des Arbeitsblatts mit
einer Einschätzung der Wahrscheinlichkeiten für rote Gummibärchen in einer Packung. In
der Aufgabe arbeiten die Schüler auf der enaktiven, ikonischen und formalen Repräsentationsebene. Zunächst sollen sie, ausgehend vom natürlichen Häufigkeitskonzept, argumentieren und einschätzen, wie viele rote Gummibärchen in einer Packung vorhanden sind. Die
Schüler können sich dabei von subjektiven Eindrücken leiten lassen oder den Laplace-Ansatz anwenden. Auch wenn es sich bei diesem Zufallsexperiment nicht um ein Glückspiel
handelt, ist die Annahme der Gleichwahrscheinlichkeit durchaus plausibel, denn warum
sollte der Hersteller eine Farbe benachteiligen. Dennoch erkennen die Schüler eine große
Unsicherheit, die mit dem Laplace-Ansatz verbunden ist. Die theoretischen Überlegungen
überzeugen außerhalb der Glücksspielwelt kaum, insbesondere dann, wenn andere subjektive Vorstellungen gegenwärtig sind. Die Überprüfung der Wahrscheinlichkeit durch den
frequentistischen Wahrscheinlichkeitsbegriff ist für die Schüler die logische Folge. Sie öffnen daher jeweils eine Packung und zählen die Anzahl der roten Gummibärchen. In allen
Packungen ist (vermutlich) eine unterschiedliche Anzahl roter Gummibärchen zu finden.
Dadurch wird deutlich, dass die absoluten und relativen Häufigkeiten bei kleinen Versuchszahlen sehr stark schwanken. Daher lässt sich der Zufall mit einer kleinen Versuchszahl
kaum einschätzen. Den Schülern wird so die Bedeutung des Stichprobenumfangs bewusst.150
Des Weiteren wird der Unterschied zwischen der relativen Häufigkeit und der Wahrscheinlichkeit sehr deutlich. Relative Häufigkeiten beschreiben eine vergangene Versuchsdurchführung, dagegen blicken Wahrscheinlichkeiten in die Zukunft und stellen für diese einen
148
Steinbring: Zur Entwicklung, S. 33.
Bieler: Gesetze, S. 18.
Henze: Stochastik für Einsteiger, S. 19.
150
Borovcnik: Zum Anwendungsproblem, S. 30.
149
39
Schätzwert dar. Den Schülern werden zwangsläufig zwei Fragestellungen in den Sinn kommen, die im weiteren Verlauf des Arbeitsblattes gelöst werden: Wie viele Versuchsdurchführungen muss ich machen, bis ich einen guten Schätzwert gefunden habe? Wenn ich einen
Schätzwert gefunden habe bzw. mir ein Schätzwert genannt wurde, wie gut kann ich diesem
vertrauen? Diese Fragestellungen sollen in Aufgabe 2 und 3 mit Hilfe der bekannten Zufallsgeneratoren, wie der Münze und dem Würfel, analysiert werden.151
Bevor die Schüler die Fragestellungen bearbeiten, führen sie in Aufgabe 1 für das Problem
der roten Gummibärchen eine Datenanalyse durch. Den Schülern soll dadurch der Übergang
von der Datenanalyse zur Wahrscheinlichkeitstheorie erleichtert werden. Insbesondere
durch die hohe Datenvielfalt in den Medien (Fernsehen, Zeitungen usw.) ist eine starke Verknüpfung dieser beiden Sachbereiche wichtig. Auch spricht für diese Verbindung das Bruner‘sche Spiralprinzip. Oftmals stellen die Schüler nach einer Datenanalyse die Frage „Ist
das immer so?“ oder „Bleibt das auch in Zukunft so?“ Somit können Fragestellungen aus
dem Teilbereich der Wahrscheinlichkeitstheorie angesprochen werden.152
Die Schüler erkennen in dieser Aufgabe, wie wichtig es ist, mit Daten zu argumentieren.
Jedoch bleibt immer eine gewisse Unsicherheit, da nicht alle Packungen geöffnet werden
können. So werden nur möglichst gute Schätzungen erzielt. Wie schon beim Laplace-Modell
gelingt es der Stochastik bzw. der Mathematik nicht, absolute Sicherheit zu garantieren.
Beim Laplace-Modell rührt diese Unsicherheit von der Nichtbeweisbarkeit der Modellannahme. Beim frequentistischen Wahrscheinlichkeitsbegriff bildet das empirische Gesetz der
großen Zahlen die Grundlage. Zwar stabilisieren sich die relativen Häufigkeiten mit genügend großer Versuchszahl, doch bleibt unklar, was stabilisieren bzw. genügend groß bedeutet.153
Nichtdestotrotz können die Schüler durch die Datenanalyse bereits Entscheidungen unter
Unsicherheit treffen.154 Die Analyse sollte in Gruppenarbeit erfolgen, damit bei der späteren
Besprechung der Aufgaben mehrere Versuchsreihen und damit unterschiedliche Reihen vorliegen. Die Schüler erkennen so, dass bei kleinen Versuchsreihen die absoluten und relativen
Häufigkeiten schwanken. Mit wachsender Versuchszahl stabilisieren sich die relativen Häufigkeiten. Die absoluten Häufigkeiten hingegen überschreiten mit wachsender Versuchszahl
jede vorgegebene Grenze. Genauer gesagt stabilisiert sich beispielsweise beim Münzwurf
151
Engel; Vogel: Von M&Ms, S. 12.
Meyer: Stochastik wirklich verstehen, S. 20.
152
Eichler; Vogel: Leitidee Daten und Zufall, S. 160.
153
Dabrock: Zur Erarbeitung, S. 37.
154
Ein Beispiel dafür ist die Explorative Datenanalyse. Vgl. Biehler: Statistische Kompetenz, S. 112.
40
k
zwar die relative Häufigkeit für Kopf auf . Jedoch überschreitet der „Betrag der Differenz
n
n
zwischen Anzahl Kopf und erwarteter Anzahl Kopf“ = |k - 2| mit einer Wahrscheinlichkeit,
die stochastisch gegen 1 konvergiert, jede vorgegebene natürliche Zahl.155
Die abschließende Frage, die eine Einschätzung der Wahrscheinlichkeit nach der Datenanalyse verlangt, verdeutlicht, dass es sich um eine subjektive Schätzung der Wahrscheinlichkeit auf Basis der relativen Häufigkeit handelt. Schließlich hängt die Schätzung von der Datenreihe und von der Rundung der einzelnen Schüler ab und kann dadurch variieren.156
Darüber hinaus kann das Beispiel der Anzahl der roten Gummibärchen in einer Packung in
der beurteilenden Statistik wieder aufgegriffen werden. So kann beispielsweise die Prognose, dass eine Gleichverteilung der Gummibärchen vorliegt, mit Hilfe der beurteilenden
Statistik überprüft werden. Diese beleuchtet, ob ein Modell zur Realität passt oder nicht. Es
müssen dabei Vereinbarungen getroffen werden, wann ein Modell bzw. eine Prognose verworfen werden muss. In dieser Debatte können leicht Fehler erster (fehlerhafte Beibehaltung
des Laplace-Modells) und zweiter Art (fehlerhafte Verwerfung des Laplace-Modells) durch
die Lehrkraft eingebaut werden, damit die Schüler zum Argumentieren motiviert werden.
Dabei soll die Wechselwirkung zwischen einer Entscheidungsregel und den Fehlern deutlich
werden. Die Realität kann also nur möglichst genau beschrieben werden, da der genaue Abfüllvorgang der Gummibärchen nicht bekannt ist.157
Aufgabe 2 geht der Frage nach, wie oft eine Münze geworfen werden muss, damit die relative Häufigkeit ein guter Schätzwert ist. Der Kontext eines Chinesisch-Multiple-ChoiceTests mit zwei Antwortmöglichkeiten schafft die Möglichkeit einer Modellierung mit einer
Münze. Dies kann für einen anderen Schultest nicht aufrechterhalten werden, da die Wahrscheinlichkeit einer richtigen Antwort nicht bei jeder Frage gleich hoch ist. Damit würde die
Unabhängigkeitsannahme der Zufallsversuche aufgegeben werden, die aber die wichtigste
Voraussetzung des frequentistischen Wahrscheinlichkeitsbegriffs darstellt.158 Der Zufallsgenerator der Münze wird dabei verwendet, um den Schülern beim Erkunden des frequentistischen Wahrscheinlichkeitsbegriffs „Sicherheit“ zu geben. In den letzten Sitzungen haben
die Schüler den Laplace-Wahrscheinlichkeitsbegriff vertieft behandelt und wissen, dass er
155
Meyer: Stochastik wirklich verstehen, S. 22.
Engel; Vogel: Von M&Ms, S. 15.
157
An dieser Stelle wird darauf verzichtet, eine Aufgabe zu den Fehlerarten zu stellen. Die Schüler sollen zuerst
den subjektiven Wahrscheinlichkeitsbegriff und die bedingte Wahrscheinlichkeit kennen lernen, um angemessen über die beurteilende Statistik diskutieren zu können, da die Fehler 1. und 2. Art bedingte Wahrscheinlichkeiten sind. Vgl. Diepgen: Was Schüler, S. 34.
Vgl. auch Beck-Bornholdt; Dubben: Schein der Weisen.
158
Dahl: Unabhängigkeit Unterrichten, S. 5.
156
41
im Bereich der Glücksspiele Vorteile hat. So können Wahrscheinlichkeiten a priori bestimmt
1
werden (bei der Münze die Wahrscheinlichkeit 2). Somit wird ersichtlich, dass der Fokus in
den folgenden Aufgabenteilen auf der Durchdringung des frequentistischen Wahrscheinlichkeitsmodells und nicht auf einer Modellierungsaufgabe liegt.159
Im ersten Aufgabenteil (2a) sollen sich die Schüler zwischen zwei Testformen (70% von 10
oder 70% von 50 korrekt gelösten Fragen zum Bestehen des Tests) entscheiden. Während
der Besprechung der einzelnen Itemergebnisse sollen die Schüler jeweils die relativen Häufigkeiten ihrer richtigen Antworten auf eine Overhead-Folie übertragen. An dieser Stelle
kann darüber diskutiert werden, ob diese Punkte (Anzahl der Versuche; Relative Häufigkeit),
wie in vielen Lehrbüchern, miteinander verbunden werden sollten. Den Polygonzug zu
zeichnen hätte lediglich den Vorteil, einer besseren Visualisierung der Stabilisation. Gleichzeitig wird unreflektiert von einem diskreten in einen kontinuierlichen Wahrscheinlichkeitsraum gewechselt. Dies kann, wie im Laplace-Modell gesehen, gravierende Folgen haben.
Daher wird empfohlen den Polygonzug nicht zu zeichnen, sondern es bei einer Abtragung
der Punkte zu belassen.
Beim Abtragen sollen die Schüler eine Folie benutzen, damit die Graphen auf einem Overheadprojektor übereinander gelegt werden und so Gemeinsamkeiten und Unterschiede festgestellt werden können.160 Somit werden die Erkenntnisse der letzten Aufgabe (Aufgabe 1)
vertieft: Die relativen Häufigkeiten schwanken zu Beginn der Versuchsreihe und stabilisieren sich im Laufe der Zeit. Dabei können die Schüler die Situation sowohl statisch als auch
dynamisch analysieren, da sie eine Versuchsreihe im Verlauf betrachten oder mehrere Versuchsreihen an verschiedenen Stellen vergleichen können.161
Durch die Ausführung der Münzwürfe wird den Schülern die Bedeutung einer Simulation
im Bereich des frequentistischen Wahrscheinlichkeitsbegriffs bewusst.162 Ebenso können sie
durch einen Vergleich einer Computersimulation von 50 Versuchen mit ihren Graphen erkennen, dass die Computersimulation die gleichen Eigenschaften aufweist. So erkennen die
Schüler, dass der Computereinsatz ihre Arbeit wesentlich vereinfacht und mit einer „normalen“ Versuchsdurchführung gleichberechtigt anzusehen ist.163 Dies bedeutet auch, dass die
Computersimulation ebenfalls subjektiv ist, da jede etwas anders aussieht und dementsprechend auch zu einer anderen Schätzung der Wahrscheinlichkeit führt. Zusätzlich basiert eine
159
Hergel: Wahrscheinlich? Zufall?, S 7.
Schanz: Statistik und Wahrscheinlichkeitsrechnung, S. 48.
161
Schnell: Muster und Varibialität, S. 20.
162
Biehler: Computers in Probability, S. 173.
163
Biehler; Maxara: Integration, S. 45.
160
42
Simulation auf Modellannahmen (hier: Laplace-Wahrscheinlichkeit der Münze). Diese müssen bewusst getroffen und reflektiert werden. Eine Simulation entbindet die Schüler nicht
von dem Modellbildungsprozess, sondern erleichtert ihnen nur die Arbeit innerhalb eines
Modells.164 Aus diesem Grund wird in dieser Arbeit ein großer Wert auf die Chancen und
Risiken der einzelnen Modelle gelegt. Die Schüler können so „den eigentlichen Charakter
des Zufalls“165 erlernen.
Im Aufgabenteil c) arbeiten die Schüler mit den Graphen und analysieren sie. Durch den
Vergleich der Testformen fällt auf, dass beim Test mit zehn Fragen mehr Schüler bestanden
haben als beim Test mit 50 Fragen. Durch die übereinandergelegten Graphen wird ersichtlich, dass sechsmal Wappen in zehn Versuchen öfter angenommen wird als 35-mal Wappen
in 50 Versuchen. Daher ist es wahrscheinlicher, dass als Anteil von 70 % „Wappen“ bei zehn
Würfen angenommen wird. Die Schüler erlernen, dass große Abweichungen der relativen
Häufigkeiten von der Wahrscheinlichkeit nur bei kleinen Datensätzen vorkommen können,
da die relativen Häufigkeiten bei dieser Versuchszahl noch stark schwanken. Eine konsequente Unterscheidung zwischen relativer Häufigkeit und Wahrscheinlichkeit ist für dieses
Verständnis hilfreich.166
In der zweiten Frage des Aufgabenteils 2b) wird die Stabilisation des empirischen Gesetzes
der großen Zahlen genauer betrachtet. Die bisherigen Aufgaben brachten den Schülern die
Erkenntnis, dass durch eine Erhöhung der Versuchszahl die Graphen immer ähnlicher werden und sich einem gewissen Wert annähern.
167
Zur Definition der Wahrscheinlichkeit
könnten die Schüler das Zufallsexperiment unendlich oft (im Kopf) wiederholen und den
Limes der relativen Häufigkeit als Definition der Wahrscheinlichkeit verwenden. Diese Idee
hatte auch Richard von Mises im Jahre 1919. Grundlage sollte dabei die Verwendung eines
analytischen Grenzwertes sein. Jedoch garantiert das empirische Gesetz der großen Zahlen
einen analytischen Grenzwert (leider) nicht.168 Bevor die Schüler in Aufgabe 2d) den formalen Gegenbeweis zur Idee von Mises ordnen, sollen sie anhand ihrer Graphen untersuchen,
ob die relative Häufigkeit immer näher an die Laplace-Wahrscheinlichkeit kommt:169
164
Eichler; Vogel: Leitidee Daten und Zufall, S. 163.
Tietze; Klika; Wolpers: Didaktik des Mathematikunterrichts, S. 230.
165
Wollring: Ein Beispiel, S. 3.
166
Lergenmüller: Mathematik Neue Wege, S. 31.
167
Eine Möglichkeit bereits in der Grundschule das Gefühl für das empirische Gesetz der großen Zahlen zu
erlangen, stellt das Spiel „Der Wettkönig“ dar. Allerdings wird das Gesetz der großen Zahlen gilt lediglich zur
Bestätigung des Laplace-Modells verwendet. Damit werden die Zufallsschwankungen bei großen Versuchszahlen unerwünscht. Vgl. Hußmann; Prediger: Je größer.
168
Mathematisch beweisbar ist lediglich eine Stabilisierung, da lim ℎ𝑛+𝑠 (𝐴) − ℎ𝑛 (𝐴) = 0. Vgl. Eichler; Vo𝑛→∞
gel: Leitfaden Stochastik, S. 104.
169
Lergenmüller: Mathematik Neue Wege, S. 29.
43
Abbildung 8: Empirisches Gesetz der großen Zahlen.
Quelle: Lergenmüller: Mathematik Neue Wege, S. 29.
An Graphen wie in Abbildung 8 können die Schüler erkennen, dass sich die relative Häufigkeit sehr dicht an die Laplace-Wahrscheinlichkeit annähern, sich danach aber wieder ein
bisschen entfernen kann. Besonders schön ist das am roten Graphen zwischen dem 70. und
100. Wurf zu erkennen. An dieser Stelle sollen die Schüler ein Gefühl für die Schwankungen
der relativen Häufigkeiten gewinnen. Sie kommen also nicht „immer näher“ an die LaplaceWahrscheinlichkeit heran.
Die Schüler verbinden mit dem Ausdruck „immer näher kommen“ den Konvergenzbegriff
aus der Analysis. Damit sich die Schüler an die mathematische Sprache gewöhnen, wurde
der Gegenbeweis in Papierschnipsel zerschnitten und den Schülern zum Ordnen überlassen.
Auf diese Art und Weise werden die Schüler formal entlastet und können sich stärker auf
den Inhalt des Satzes konzentrieren, indem sie die Argumentationsstruktur ordnen.170 Letztendlich ermitteln die Schüler folgenden Gegenbeweis:
Wenn für ein Ereignis E eine reelle Zahl P(E) existiert, für die P(E) = lim hm171(E) gilt, dann müsste
m→∞
für jede positive Zahl ɛ eine positive Zahl mɛ existieren, so dass |P(E) – hm(E) < ɛ| für alle m ≤ mɛ. Aber
genau das lässt sich nicht garantieren. Denn nach der Wahl eines ɛ>0 wird die relative Häufigkeit in
den sogenannten ɛ-Schlauch P(E) ± ɛ hineinlaufen, aber kann ihn auch wieder verlassen.172
Eine Konvergenz im analytischen Sinne hätte Sicherheit gebracht, da sich die Werte ab einer
gewissen Versuchszahl nicht um mehr als ein gewisses ε unterscheiden. Die Graphen der
Schüler zeigen jedoch, dass die relativen Häufigkeiten in die ε-Umgebung hineinlaufen, sie
aber danach wieder verlassen können (vgl. Abbildung 9). Statt dieser recht wackligen Tendenz kennen sie aus vielen Beispielen der Analysis eine straffe Konvergenz. Die Schüler
erkennen so die Schönheit eines analytischen Grenzwertes.173
170
Brunner: Ein Prozessmodell, S. 270.
hm bezeichnet die relative Häufigkeit in Abhängigkeit von m. Hier kann zusätzlich wieder thematisiert werden, dass hm ebenfalls von der Versuchsreihe abhängt und insofern subjektiv ist.
172
Büchter; Henn: Elementare Stochastik, S. 175.
173 Fischer; Lehner; Puchert: Einführung in die Stochastik, S. 76.
Barth: Leistungskurs, S. 70.
171
44
Abbildung 9: ε-Schlauch.
Quelle: Büchter; Henn: Elementare Stochastik, S. 175.
Die angestrebte Definition der Wahrscheinlichkeit konnte also von Mises durch das empirische Gesetz der großen Zahlen nicht erreichen. Dieses dient „nur“ dazu (theoretisch unendlich oft) wiederholbaren Ereignissen Wahrscheinlichkeiten zuzuschreiben. Dahinter steht
die Vorstellung, dass die relativen Häufigkeiten stochastisch konvergieren. Das
Bernoulli‘sche Gesetz der großen Zahlen (=schwaches Gesetz der großen Zahlen) macht mit
Hilfe des axiomatischen Wahrscheinlichkeitsbegriffs eine mathematische Aussage darüber,
wie wahrscheinlich das Verbleiben der relativen Häufigkeiten im ɛ-Schlauch ist (Vgl. Arbeitsblatt „Der axiomatische Wahrscheinlichkeitsbegriff III). Damit zeigt es, wie die relative
Häufigkeit und die Wahrscheinlichkeit zusammenhängen. Das schwache Gesetz der großen
Zahlen stellt im Gegensatz zum viel komplexeren starken Gesetz der großen Zahlen einen
Lebensbezug für die Schüler dar. Den Fokus auf die starke stochastische Konvergenz der
unendlichen Versuchsreihen zu legen, würde die Einsicht, dass die relativen Häufigkeiten
schwanken, verhindern. Auch wenn die Schwankungen unangenehm sein können, ist es jedoch wichtig mit dieser Unsicherheit umzugehen, damit der Charakter der Stochastik verdeutlicht wird.174
Aufgabe 3 versucht die Zufallsschwankungen experimentell zu erfassen. Hierbei soll das
1
-
√n
Gesetz ähnlich wie das empirische Gesetz der großen Zahlen als eine Art Naturgesetz angesehen werden und eine Verbindung zwischen Intuition und beurteilender Statistik herstellen.
174
Riemer: Stochastische Probleme, S. 19.
Bender: Grundvorstellungen und Grundverständnisse, S. 17.
45
Das mathematische Pendant stellt dabei der Zentrale Grenzwertsatz175 dar. Die Schüler benutzen die in Aufgabe 2 erstellten Werte der Simulation und erhalten in etwa diese Tabelle
(vgl.Tabelle 3):176
𝟏
Tabelle 3: √𝒏 – Gesetz.
N
25
100
400
1000
Relative Häufigkeit
Individuell verschieden
Individuell verschieden
Individuell verschieden
Individuell verschieden
Intervall für h (im Plenum)
0,5±0,2
0,5±0,1
0,5±0,05
0,5±0,01
Quelle: Lergenmüller: Mathematik Neue Wege, S. 33.
So wird wiederum deutlich, dass die relativen Häufigkeiten von der Versuchsreihe stark abhängig sind. Die Intervallgrößen zeigen, dass die Standardabweichung für höhere Versuchszahlen immer geringer wird. Diese Tatsache ist den Schülern aus der Sek. I bewusst. Im
letzten Schritt kann die Intervallgröße durch
1
√n
abgeschätzt werden. Dieser Schritt muss über
die Werte begründet werden.177
Den Abschluss dieses Arbeitsblattes bilden Übungen zum
1
-Gesetz. In Aufgabe 3b) wird
√n
ein Würfel 200 Mal gewürfelt. Mit 95% Sicherheit kann davon ausgegangen werden, dass
die relative Häufigkeit im Bereich des Intervalls [0,43; 0,57] liegt.178
Weiterhin beschäftigt sich die Aufgabe 3c) mit einer Einschätzung der Wurfanzahl, falls ein
bestimmtes Prognoseintervall mit einer 95%igen Sicherheit erreicht werden soll. Diese
Wurfanzahl wird hierbei grundsätzlich unterschätzt. In dieser Aufgabe wurde ein Prognoseintervall von [0,48; 0,52] angegeben. Mit Hilfe des
Versuchszahl n:
1
√n
1
-Gesetzes errechnen die Schüler die
√n
1
= 0,02 ⇒ √n = 0,02 ⇒ n = 502 = 2500. Dies verdeutlicht die Schwäche
des frequentistischen Wahrscheinlichkeitsmodells. Es müssen sehr viele Versuche durchgeführt werden, um zu einer genauen Schätzung zu gelangen. Trotzdem ist diese noch mit einer
Unsicherheit (95%-Prognoseintervall) verbunden. 179
175
Dieser führt zu weit über die Einführung der Wahrscheinlichkeitsbegriffe hinaus und wird daher in dieser
Arbeit nicht behandelt, sondern nur angeschnitten. Im Fokus soll hier die zentrale Bedeutung des Stichprobenumfangs stehen. Vgl. Riemer: Anmerkungen zu Buth, S. 23.
Vgl. Biehler; Engel: Stochastik, S. 241.
176
Lergenmüller: Mathematik Neue Wege, S. 33.
177
Freudenthal: Empirical Law, S. 486.
Vanscó; Warmuth: Schwierigkeiten, S. 22.
178
Lergenmüller: Mathematik Neue Wege, S. 33.
179
Ebd. S. 33.
46
In der Vertiefung behandeln die Schüler erneut die „Wette des Chevaliers“. Die Schüler
haben bereits mit Hilfe des Laplace-Wahrscheinlichkeitsbegriffs die Wahrscheinlichkeiten
0,482 bzw. 0,509 errechnet. Das
1
-Gesetz liefert das Ergebnis, dass der Chevalier 3.086-
√n
bzw. 12.345-mal würfeln musste, um mit 95%iger Sicherheit diese Unterschiede bemerkt zu
haben.180
Darüber hinaus erfolgt im zweiten Teil der Vertiefung eine Reflexion des frequentistischen
Wahrscheinlichkeitsbegriffs anhand eines Zitats Bernoullis181. Er stellte sich die Frage, wie
sich die relativen Häufigkeiten der Wahrscheinlichkeit annähern: Werden die relativen Häufigkeiten bei genügend großer Anzahl der Wiederholungen das „wahre Verhältnis“, das heißt
die Wahrscheinlichkeit, erreichen oder kann die Wahrscheinlichkeit nur bis zu einem gewissen Grad der Gewissheit gefunden werden.182 Mit dieser Fragestellung wirft Bernoulli in
seinem Zitat beide Problematiken des empirischen Gesetzes der großen Zahlen auf. Er stellte
sich die Frage, was „genügend groß“ bedeuten soll und problematisiert vor allem die Art der
Konvergenz (Stabilisation) um die innewohnende Wahrscheinlichkeit. Es wird nochmals
deutlich, dass durch den frequentistischen Wahrscheinlichkeitsbegriff lediglich Wahrscheinlichkeiten berechnet werden können. Was Wahrscheinlichkeiten sind, kann nicht ausgedrückt werden. Daher bleibt die Frage, in welchem Verhältnis die relativen Häufigkeiten und
die Wahrscheinlichkeit stehen, zunächst offen und kann auf dem Arbeitsblatt aus der ersten
Sitzung notiert werden. Beim Aufbau der Axiomatik wird sich an diesen Problemen orientiert, um den Schülern Sinn und Zweck einer Axiomatik deutlich zu machen.183
3.3.2 Arbeitsblatt II - Der Begriff der Unabhängigkeit
Bei der Bestimmung von Wahrscheinlichkeiten im frequentistischen Modell spielt die Unabhängigkeit der einzelnen Zufallsversuche eine große Rolle. Dies soll durch einen einleitenden Zeitungsartikel deutlich werden: In diesem wurde ein alkoholisierter Systemanalytiker kurz vor dem Einsteigen in sein Auto von der Polizei bemerkt und ermahnt nicht nach
Hause zu fahren. Kurze Zeit später kehrte die Polizei zurück und sah den Systemanalytiker
im Auto wegfahren. Als die Polizei ihn anhielt, reagierte der Systemanalytiker verwirrt. Er
ging vom frequentistischen Wahrscheinlichkeitsbegriff aus und fasst die einzelnen Tage als
180
Ebd. S. 36.
Bernoulli trug mit seinem Werk „Ars Conjectandi“ wesentlich zur Entwicklung der Stochastik bei.
182
Ineichen: Würfel und Wahrscheinlichkeiten, S. 7.
183
Büchter; Henn: Elementare Stochastik, S. 177.
Kütting: Didaktik der Stochastik, S. 50.
Hacking: Emergence of Probability, S.143.
181
47
̅̅̅̅̅̅̅̅̅̅̅̅ auf. Daraus beZufallsexperiment mit den Elementarereignissen Kontrolle und Kontrolle
rechnet er die Wahrscheinlichkeit und kommt zu dem Schluss, dass die nächste Kontrolle
erst in 100 Jahren stattfinden wird. Dabei vernachlässigt er allerdings, dass die erste und die
zweite Kontrolle nicht unabhängig voneinander waren. Der Polizei fiel der Systemanalytiker
bereits im Vorhinein auf, als er betrunken Autofahren wollte. Dieses Faktum erhöht natürlich
die Wahrscheinlichkeit, dass er kurz danach wieder kontrolliert wird. Die Schüler erkennen
so, dass die Unabhängigkeit im frequentistischen Wahrscheinlichkeitsmodell eine notwendige Voraussetzung darstellt. Erst durch ihn können Daten zu theoretischen Modellen ausgebaut werden.184 Die Schüler sollen die Annahme der stochastischen Unabhängigkeit ähnlich wie bei der Laplace-Wahrscheinlichkeit stets als Vereinfachung bzw. Modellbildung
auffassen und gegebenenfalls im Nachhinein reflektieren. Sie müssen also hinterfragen, ob
sich die einzelnen Versuche gegenseitig beeinflussen. Erst wenn sie dies als Modellannahme
akzeptiert haben, greift der frequentistische Wahrscheinlichkeitsbegriff, da die Situation und
damit auch die „innewohnende“ Wahrscheinlichkeit in jeder Wiederholung des Ereignisses
gleich bleiben. Dies ist auch der Grund, warum bei der Behandlung des frequentistischen
Modells öfters Laplace-Zufallsgeneratoren verwendet werden. Dort ist die Modellannahme
der stochastischen Unabhängigkeit sinnvoll, das heißt, dass beispielsweise die Wahrschein1
lichkeit eine 6 zu würfeln in jedem Versuch 6 beträgt. Dadurch können Simulationen ausgeführt und Eigenschaften des frequentistischen Modells erkundet werden.185
Dies wird im letzten Teil der ersten Aufgabe durch einen Vergleich von zwei Situationen
vertieft, die die Schüler schon in Aufgabe 3c) des Arbeitsblattes „Der Laplace-Wahrscheinlichkeitsbegriff II“ behandelt haben. Dort wurden im ersten Teil der Aufgabe abwechselnd
Lose ohne Zurücklegen aus einem Hut gezogen. In dieser Situation wird ersichtlich, dass der
vorherige Zug die Wahrscheinlichkeit im nächsten Zug beeinflusst, da sich insbesondere die
Ergebnismenge ändert. Im Gegensatz dazu steht das mehrmalige Drehen eines Glücksrades,
da die Wahrscheinlichkeit vom vorherigen Zug unbeeinflusst bleibt.186 Daher können die
Schüler folgende Definition der stochastischen Unabhängigkeit auf ihrem Arbeitsblatt notieren:
184
Steinbring: Wahrscheinlichkeit, S. 228.
Eichler; Vogel: Leitidee Daten und Zufall, S. 204.
186
Diese Tatsache kann mit Hilfe eines Einheitsquadrats verdeutlicht werden. Die Ereignisse A und B sind
genau dann unabhängig, wenn das empirische Einheitsquadrat bündig abschließt. Hier wird deutlich, dass die
Unabhängigkeit ebenfalls lediglich ein Modell darstellt, das (fast) nie mit empirischen Daten erreicht werden
kann. Vgl. Ebd. S. 183.
185
48
Es sei (Ω, P(Ω), P) ein endlicher Wahrscheinlichkeitsraum. Die Ereignisse A, B ∈ P(Ω) heißen stochastisch unabhängig genau dann, wenn gilt: P(A∩B) = P(A)·P(B).187
In der zweiten Aufgabe wird die stochastische Unabhängigkeit auf mehrere Ereignisse erweitert. Die Schüler hinterfragen also die Bedeutung der Beeinflussung der einzelnen Ereignisse. Dazu betrachten sie ein Beispiel, dass vom russischen Mathematiker Bernstein entwickelt wurde. Dort ist ein Tetraeder gegeben, bei dem die vier Flächen durch rot (R), blau
(B), grün (G) und die letzte durch alle drei Farben gekennzeichnet sind. Die Schüler sollen
zunächst untersuchen, ob die Ereignisse beim Tetraederwurf paarweise unabhängig sind.
Dazu bestimmen sie die Laplace-Wahrscheinlichkeit für die einzelnen Farben: P(R) = P(B)
1
1
= P(G) = 2. Danach berechnen sie P(R∩B) = P(R∩G) = P(B∩G) = 4. Durch die in Aufgabe
1 aufgestellte Definition der Unabhängigkeit von zwei Ereignissen erkennen die Schüler,
dass die Ereignisse paarweise unabhängig sind.
Im Aufgabenteil b) stellen die Schüler zunächst eine Vermutung über die Wahrscheinlichkeit P(R∩B∩G) auf. Sie könnten aus der paarweisen Unabhängigkeit der Ereignisse vermu1 1 1
1
ten, dass P(R∩B∩G) = P(R) ∙ P(B) ∙ P(G) = 2 ∙ 2 ∙ 2 = 8 beträgt. Anschließend überprüfen sie
1
diese Vermutung, wobei sie feststellen, dass P(R∩ B∩G) = 4 beträgt, da nur eine Seite des
Tetraeders aus allen Farben besteht. Die Schüler erkennen so, dass ihre Vermutung falsch
war und bei der Überprüfung der Unabhängigkeit alle möglichen Kombinationen (2n -1-n
Stück) auf ihre Gültigkeit betrachtet werden müssen.188
Die Schüler stellen an der Definition der stochastischen Unabhängigkeit fest, dass es sich
hierbei um einen theoretischen Begriff handelt, der mengentheoretisch definiert wurde. Daher bietet sich bei der Untersuchung des Unabhängigkeitsbegriffs das Laplace-Wahrscheinlichkeitsmodell an, das ebenfalls wie die Axiomatik Kolmogorovs auf der Mengentheorie
basiert. Deswegen sollte auch die Bezeichnung „nicht stochastisch unabhängig“ nicht mit
„keinem realen Einfluss in der Wirklichkeit“ interpretiert werden. Allerdings ist es für den
Modellierungsprozess wichtig die andere Richtung zu betrachten. Die Schüler interpretieren
„keinen realen Einfluss“ mit „stochastisch unabhängig“ und bestimmen dann die Wahrscheinlichkeit über den frequentistischen Wahrscheinlichkeitsbegriff.189
187
An dieser Stelle wurde die Schreibweise mit Hilfe der Axiomatik gewählt. Für die Schüler reicht der zweite
Teil der Definition aus. Vgl. Kütting; Sauer; Padberg: Elementare Stochastik, S. 177.
188
Ebd. S. 179.
189
Ebd. S. 120.
49
Dies hat auch Auswirkungen auf die Wahrscheinlichkeitsverteilungen. Für die Entwicklung
der Wahrscheinlichkeitstheorie spielt (in dieser Arbeit) vor allem die Modellierung der Binomialverteilung190 eine große Rolle. Problematisch daran ist, dass oft von einer Unabhängigkeit der Einzelversuche ausgegangen wird, die insbesondere bei einer realitätsbezogenen
Interpretation Realität nicht haltbar ist. In einer Abituraufgabe wurde so von der Trefferquote
des Basketballers Dirk Nowitzki, die über die relative Häufigkeit bestimmt wurde, eine Binomialverteilung erstellt. Jedoch können die einzelnen Würfe eigentlich nicht als unabhängig angesehen werden, da hierbei die Tagesform, die Drucksituationen etc. vernachlässigt
werden. Es muss daher ganz klar gemacht werden, dass es sich hierbei um ein Modell und
nicht um die Realität handelt. Eine Interpretation und Reflexion der Ergebnisse ist notwendig.191 Um auf dieses Verständnis für den Aufbau der Wahrscheinlichkeitsverteilungen auf
dem nächsten Arbeitsblatt (Der frequentistische Wahrscheinlichkeitsbegriff III) zurückgreifen zu können, diskutieren die Schüler, in wie fern die Trefferquote Dirk Nowitzkis für jeden
seiner Würfe gilt.
Den Abschluss des Arbeitsblattes (Aufgabe 3) bildet die Wiederholung des Themenblocks
„frequentistischer Wahrscheinlichkeitsbegriff“ anhand des Intuitionsarbeitsblatts. Der erste
Aufgabenteil vertieft das Verständnis des empirischen Gesetzes der großen Zahlen durch
das im Kapitel „Sind Menschen gute Statistiker?“ vorgestellte Beispiel der Krankenhausaufgabe. Eine intuitive Vorstellung für das
1
-Gesetzes würde diese Einsicht verstärken.192 Au-
√n
ßerdem soll den Schülern bewusst werden, dass sich die Schwankung der absoluten Häufigkeiten bei wachsender Versuchszahl keineswegs stabilisiert und jede vorgegebene Grenze
überschreitet. Dafür steht der Gambler's Fallacy, der häufig beim Roulette zu beobachten
ist.193 Eng damit verbunden ist die Missachtung der Unabhängigkeit der Roulettedurchgänge. Der Ausspruch „Die Roulettkugel hat kein Gedächtnis“ drückt die Unabhängigkeitsannahme aus und verdeutlicht, dass die Wahrscheinlichkeit in jedem Durchgang die gleiche
ist. Hingegen werden die Karten beim Kartenspiel Black-Jack nicht wieder in den Stapel
190
Die gilt natürlich für alle weiteren Verteilungen, die als Modell für statistische Daten dienen. Außerdem
werden schon bei der Datenbeschaffung Unabhängigkeitsannahmen getätigt. So soll die Art und Weise der
Erhebung unabhängig von Ort, Person und Zeit sein. Vgl. Eichler; Vogel: Leitidee Daten und Zufall, S. 204.
191
Diepgen: Ein Witz, S. 23.
Mittag: Statistik, S. 175.
192
Biehler; Maxara: Integration, S. 50.
193
Dieser Fehlschluss kann mit Hilfe von Runs besser verstanden werden. An dieser Stelle wurde diese Thematik aber reduziert, weil zum einen der Logarithmus eine entscheidende Rolle spielt und zum anderen die
Binomialverteilung bei den Schülern präsent sein muss. Eichelsbacher: Mit Runs, S. 4.
50
gemischt. Daher kann aus wahrscheinlichkeitstheoretischer Sicht, die Chance zu gewinnen
erhöht werden, wenn die abgeworfenen Karten „gezählt werden“.194
Die Intuitionsaufgabe wird durch zwei nicht ernst gemeinte Aussagen abgeschlossen, da die
Unabhängigkeitsannahme für den Aufbau der Wahrscheinlichkeitstheorie zentral ist.195 In
der Aussage „Ein Flugreisender, der Angst vor Attentaten hat, sollte stets eine Bombe mit
sich führen. Die Wahrscheinlichkeit, dass gleichzeitig zwei Bomben an Bord sind, ist fast
Null!“ wird fälschlicherweise mit einer nicht vorhandenen Unabhängigkeit argumentiert.196
Die über den frequentistischen Wahrscheinlichkeitsbegriff ermittelten Wahrscheinlichkeiten
für eine Bombe, können nicht gemäß den Pfadregeln miteinander multipliziert werden, um
so die Wahrscheinlichkeit von zwei Bomben zu ermitteln.197 Dagegen wird im zweiten Beispiel nach Polya von einer Abhängigkeit der Ereignisse ausgegangen, die in der Realität
nicht tragfähig ist. Hinter dem Beispiel Polyas steckt die Vorstellung eines Ziehens ohne
Zurücklegen (wie beim Beispiel der abwechselnden Losziehung aus der Urne):
„Der Arzt eröffnet dem Patienten nach der Untersuchung: ‚Also, die Lage ist ernst. Sie sind sehr krank;
statistisch gesehen überleben 9 von 10 Menschen diese Krankheit nicht.‘ Der Patient erbleicht. ‚Sie
haben aber Glück‘, beruhigt der Arzt. ‚Ich hatte schon neun Patienten mit den gleichen Symptomen,
und die sind alle tot.‘
Diese Vorstellung ist falsch, da von der Unabhängigkeit der Ereignisse ausgegangen werden
muss. Dies bedeutet, dass ein Patient in 9 von 10 Fällen stirbt, egal wie viele Patienten der
Krankheit vorher erlagen.198
3.3.3 Arbeitsblatt III - Wahrscheinlichkeitsverteilungen
Durch das vorherige Arbeitsblatt wurde betont, welche große Rolle die Modellannahme der
Unabhängigkeit für den frequentistischen Wahrscheinlichkeitsbegriff und für die Entwicklung der Wahrscheinlichkeitstheorie insgesamt einnimmt.199 Denn auch für den axiomatischen Aufbau nach Kolmogorov spielt die Unabhängigkeit eine zentrale Rolle:
„Historisch stellt die Unabhängigkeit von Experimenten und Zufallsvariablen genau jenes mathematische Konzept dar, das der Wahrscheinlichkeitstheorie ihren eigenen Stempel aufprägt." 200
194
Schupp: Das Galtonbrett, S. 13.
Beide Beispiele wirken durch die Beziehung von Gefahr/ Krankheit/ Tod besonders emotionalisierend. Dies
kann einen hohen Lerneffekt bei den Schülern bewirken. Allerdings muss die Lehrkraft im konkreten Unterricht sehr sensibel auf die aktuelle Situation der Schüler reagieren. Das gleiche gilt für diagnostische Aufgaben
im Bereich der bedingten Wahrscheinlichkeit (z.B. der Aidstest auf dem Arbeitsblatt „Der subjektive Wahrscheinlichkeitsbegriff I und II).
196
Ein ähnliches Beispiel findet sich in Dahl: Unabhängigkeit unterrichten, S. 4.
197
Bieler: Gesetze, S. 14.
198
Büchter; Henn: Elementare Stochastik, S. 209.
Bartz: Denkfallen vermeiden, S. 32.
199
Auch für die bedingte Wahrscheinlichkeit lassen sich Wahrscheinlichkeitsverteilungen erkunden. Es wurde
sich an dieser Stelle allerdings am Lehrplan orientiert. Vgl. Wickmann: Bayes-Statistik.
200
Dahl: Unabhängigkeit Unterrichten, S. 4.
195
51
Erst durch die Unabhängigkeitsannahme können Muster in Daten erkannt werden und zu
Wahrscheinlichkeitsverteilungen ausgebaut werden. Dies zeigt sich auch im Lehrplan der
gymnasialen Oberstufe in Rheinland-Pfalz, der fast komplett auf dem Begriff der Unabhängigkeit aufgebaut ist.201 Im Lehrplan nimmt die Erkundung der Binomialverteilung einen
großen Raum ein (4 von 17 Unterpunkten). Die Binomialverteilung soll auch in der ersten
Aufgabe dieses Arbeitsblattes entdeckt werden. Die Aufgabe wurde als Stationenlernen verfasst: In der Station 1 schätzen Schüler zunächst, wie ein Balkendiagramm aussehen könnte,
wenn Sie in 20 Würfe jeweils vier Münzen werfen und die Anzahl der Wappen zählen. Diese
Einschätzung kann dem subjektiven Wahrscheinlichkeitsbegriff zugeordnet werden. Zudem
ist auf Grund der Verwendung von Münzen die Hypothese der Gleichwahrscheinlichkeit
möglich. Danach führt jeder Schüler die 20 Versuche selbst aus. Die Schüler können bereits
nach 20 Würfen die Tendenz erkennen, dass sich die Wappenanzahl „um die Mitte“ konzentriert. Dies ist ein erster Hinweis darauf, dass die mögliche Hypothese der Gleichverteilung verworfen werden muss.202 Allerdings könnte das auch Zufall sein. Daher werden die
Ergebnisse der Schüler innerhalb einer Kleingruppe (circa fünf Personen) zusammengeführt.
Mit dieser gemeinsamen Versuchsreihe kann besser eingeschätzt werden, welche der geschätzten Wahrscheinlichkeitsverteilungen zutrifft.203 Hierbei wird beispielsweise bestärkt,
dass die Vermutung der Gleichverteilung verworfen werden muss.
Danach sollen die Balkendiagramme in Aufgabenteil 1b) mit den anderen Kleingruppen verglichen werden. Dabei fällt auf, dass sich alle Diagramme hinsichtlich ihrer Struktur ähneln,
aber nicht gleich aussehen. Darin erkennen die Schüler erneut das empirische Gesetz der
großen Zahlen. Dieses gilt also nicht nur für Einzelwahrscheinlichkeiten, sondern sogar für
ganze Verteilungen.204 Das erkennbare Muster motiviert zur Theoriebildung. Über Symmetrieargumente ähnlich wie beim Riemer-Quader kann aus den Häufigkeitsverteilungen der
Schüler die Binomialverteilung entdeckt werden. Dabei wird den Schülern bewusst, dass es
sich hierbei lediglich um ein Modell handelt und nicht um die Realität. Mit diesem Hintergrundwissen können die Schüler ein Baumdiagramm zeichnen, das die möglichen Ausgänge
der Laplace-Wahrscheinlichkeiten symbolisiert. Dieses Baumdiagramm erinnert die Schüler
an das Zählprinzip „Ziehen mit Beachtung der Reihenfolge (Variation) und mit Zurückle-
201
Vgl. Einleitung.
Schupp: Das Galtonbrett, S. 13.
203
Büchter: Daten und Zufall, S. 6.
204
Biehler: Denken in Verteilungen, S. 1.
202
52
1
gen“. Daher wissen sie, dass jeder Pfad die Laplace-Wahrscheinlichkeit ( )n (hier n=4) be2
sitzt.205 Hierbei wurde die Pfadregel für unabhängige Teilereignisse verwendet. Ebenso
muss die Unabhängigkeit der Münzwürfe betont werden, damit ersichtlich wird, dass die
Binomialverteilung ein Modell darstellt. Darüber hinaus kann die Vermutung der Gleichwahrscheinlichkeit erneut aufgegriffen werden. Die Schüler sollen durch eine Analyse den
Unterschied zwischen Kopf – Kopf – Kopf – Zahl – Zahl – Zahl und 3-mal Kopf - 3mal Zahl
bzw. zwischen Kopf – Zahl – Kopf – Kopf – Zahl – Kopf und 4-mal Kopf – 2-mal Zahl
erklären. Hierbei könnte die Methode des advocatus diavoli206 hilfreich sein.
Dabei werden die Schüler vermutlich über das Baumdiagramm argumentieren. Sie fassen
daher die Ausgänge so zusammen, dass sie zur Fragestellung passen. Dabei bemerken die
Schüler, dass das Zusammenfassen der Pfade mit steigender Versuchsanzahl immer undurchsichtiger wird. Um diese Anzahlen zu ermitteln, kann das Pascal‘sche Dreieck, das die
Schüler aus dem Bereich der Algebra (oder aus der Behandlung der Kombinatorik) kennen,
mit dem Baumdiagramm verglichen werden (vgl. Abbildung 10):
Abbildung 10: Baum für den vierfachen Münzwurf und das Pascal‘sche Dreieck.
Vgl. Eichler; Vogel: Leitidee Daten und Zufall, S. 220.
Diese Werte kennen die Schüler bereits vom Binomialkoeffizienten. An dieser Stelle werden
also die Algebra und die Stochastik durch den Binomialkoeffizienten miteinander verknüpft.207 Im Endeffekt können die Schüler die Wahrscheinlichkeitsverteilung für den vierfachen Münzwurf aufstellen (vgl. Tabelle 4):
Tabelle 4: Wahrscheinlichkeitsverteilung Bino-Ley.
Ereignis
Möglichkeiten
Wahrscheinlichkeit
0 Wappen
1
1 Wappen
4
2 Wappen
6
3 Wappen
4
4 Wappen
1
∑
16
1
16
4
16
6
16
4
16
1
16
1
Vgl. Eichler; Vogel: Leitidee Daten und Zufall, S. 221.
205
Schupp: Das Galtonbrett, S. 31.
Mindestens zwei Personen führen in Frage und Antwort, These und Gegenthese eine Wechselrede, in der
eine Person die Rolle des „Advocatus diaboli“ übernimmt. Sie widerspricht bewusst einer anderen Position.
207
Steinbring: Mathematische Begriffe, S. 106.
Steinbring: Zur Entwicklung, S. 20.
Engel: Wahrscheinlichkeitstheorie und Statistik, S. 103.
206
53
Intuitiv haben die Schüler dabei eine Zufallsvariable verwendet, indem sie die einzelnen
Elementarereignissen bzw. Pfade zusammengefasst haben. Allerdings wird die Zufallsvariable wegen der hohen Formalität erst bei der Entwicklung des axiomatischen Wahrscheinlichkeitsbegriffs, von dem sie elementarer Bestandteil ist, eingeführt.
Die Station 2 ist strukturgleich zur Station 1, was durch die gleich formulierten Aufgabenstellungen verdeutlicht wird. Hier betrachten die Schüler ein Galtonbrett mit 5 Ausgängen
und durchlaufen ebenfalls die Aufgabenteile a) Schätzung der Verteilung, b) Versuchsdurchführung und c) theoretische Verallgemeinerung durch das Baumdiagramm. Es wurde sich
aus zwei Gründen dazu entschieden beide Zufallsexperimente durchzuführen: Erstens haben
beide Zugänge zur Binomialverteilung Vorteile gegenüber dem anderen: Das Bino-Ley (Station 1) setzt den bekannten zweifachen Münzwurf sukzessiv zum mehrstufigen Münzwurf
fort. Damit wird an das Vorwissen der Schüler angeknüpft, das sie insbesondere auf dem
Arbeitsblatt „Der Laplace-Wahrscheinlichkeitsbegriff I“ erworben haben. Beim Galtonbrett
entsteht die empirische Binomialverteilung durch dessen Struktur. 208 Das Baumdiagramm
und das Pascal‘sche Dreieck entstehen sozusagen „vor dem Auge des Schülers“. Daher kann
das Galtonbrett, als der Zufallsgenerator und Repräsentant für die Klasse der Binomialverteilung angesehen werden.209
Zweitens erkennen die Schüler, dass das vierstufige Galton-Brett das gleiche Muster wie der
vierfache Münzwurf aufweist. Allerdings unterscheiden sich die Häufigkeitsdiagramme etwas, wodurch erneut die Unsicherheit und Variabilität statistischer Daten deutlich wird. Spätestens an dieser Stelle wird deutlich, dass „Unsicherheit nicht gleich Zufall ist, auch wenn
beide Begriffe in analoger Weise (mathematisch) beschrieben werden.“210 Dabei ist es für
die Lehrkraft und die Schüler diagnostisch besonders wertvoll, an welcher Stelle der Aufgabenteile die Schüler die Strukturgleichheit der Zufallsversuche erkennen (bei der Schätzung
der Verteilung, in der Versuchsdurchführung oder erst bei der theoretischen Verallgemeinerung).
Durch den Vergleich der Stationen (Bino-Ley und Galtonbrett) erkennen die Schüler aber
vor allem, dass das Baumdiagramm an jeden Knoten zwei mögliche Pfade aufweist. Es werden also in jedem Teilversuch zwei mögliche Ereignisse betrachtet. Hier wird der Modellcharakter erneut deutlich, da beispielsweise ein Stehenbleiben auf dem Münzrand oder im
208
Eichler; Vogel: Leitfaden Stochastik, S. 144.
Steinbring: Mathematische Begriffe, S. 107.
209
Eichler; Vogel: Leitidee Daten und Zufall, S. 225.
210
Götz; Humenberger: Das Problem, S. 11.
54
Galtonbrett nicht berücksichtigt wird. Außerdem werden die Münzwürfe und die Kugeldurchläufe als stochastisch unabhängig modelliert und somit jedem Ereignis die Wahrscheinlichkeit
1
2
zugewiesen. Diese Modellannahmen können mit den Schülern diskutiert
werden. Eine erneute Diskussion der Nowitzki-Abituraufgabe kann an dieser Stelle durchgeführt werden.211
Der Vergleich der Zufallsexperimente soll durch die Formalisierung der Binomialverteilung
abgeschlossen werden. Dabei wird der Begriff „Bernoulli-Experiment“ für einen Zufallsversuch mit zwei möglichen Ergebnissen, die als „Erfolg“ und „Misserfolg“ bezeichnet werden,
eingeführt. Die Erfolgswahrscheinlichkeit wird mit p und die Misserfolgswahrscheinlichkeit
mit q = 1-p benannt. Abschließend kann die Wahrscheinlichkeit für k Erfolge durch die Formel P(k) = (nk) ∙ pk ∙ (1 - p)n - k definiert werden.212
Ein großer Schwerpunkt sollte auf das Verständnis der Schüler gelegt werden, wie sich die
Binomialverteilung verändert, wenn die Parameter n und p verändert werden (1b). Hier kann
bzw. sollte dem Vorschlag des Lehrplans gefolgt werden und Computersimulation eingesetzt werden. Die folgende Abbildung (vgl. Abbildung 11) zeigt exemplarisch, wie ein das
Experimentieren der Schüler zusammengefasst werden kann.213
Abbildung 11: Formen der Binomialverteilung.
Eichler; Vogel: Leitidee Daten und Zufall, S. 224.
Anschließend wird im Aufgabenteil c) der Plenumsphase eine Verbindung zur Datenanalyse
und zum empirischen Gesetz der großen Zahlen gezogen. Hierzu wird erneut die Aufgabe 1
des Arbeitsblattes „Frequentistischer Wahrscheinlichkeitsbegriff“ („Warum gibt es immer
so wenige rote Gummibärchen in der Tüte?“) betrachtet. Auch hier kann durch die Untersuchung der Farbe Rot, eine Binomialverteilung modelliert werden. Hierdurch wird klar, dass
jedes Experiment, bei dem genau zwei Ereignisse möglich sind, generell durch die Binomialverteilung modelliert werden kann. Jedoch passt das Modell bei einigen Experimenten besser als bei anderen. Daher sollten die Vereinfachungen, die das Modell mit sich bringt (hier:
Unabhängigkeit der Packungen und Laplace-Annahme), diskutiert werden. Hier zeigt sich
211
Eichler; Vogel: Leitidee Daten und Zufall, S. 224.
Ebd. S. 225.
213
Ebd. S. 225.
212
55
wiederum, dass eine ausführliche Behandlung der Wahrscheinlichkeitsbegriffe elementar
wichtig für das Verständnis der Stochastik ist, da sich die Chancen und Risiken der Modelle
auch auf mehrstufige Zufallsexperimente vererben.214
Dies gilt insbesondere für die Stabilisation der empirischen Häufigkeitsverteilungen bei genügend großer Versuchszahl um die Binomialverteilung. An dieser Stelle werden ganz bewusst die Formulierungen „Stabilisation“ und „genügend groß“ verwendet, um direkt auf
die Probleme dieser Annäherung hinzuweisen. Wie in der Idee von Mises, ist die Versuchung groß, die empirischen Häufigkeitsverteilungen durch einen analytischen Grenzwert
anzunähern, um so die „objektive“ Binomialverteilung zu erhalten. Dies scheitert aus den
gleichen Gründen wie bei der relativen Häufigkeit und der Wahrscheinlichkeit. Es kann also
wiederum nur von einer stochastischen Konvergenz gesprochen werden.
An dieser Stelle soll noch darauf verzichtet werden, die Begriffe der Wahrscheinlichkeitsrechnung als Pendant zu den Begriffen der Datenanalyse einzuführen.215 Hierfür müssten
die Schüler den Begriff der Zufallsvariable kennen, den die Schüler erst beim axiomatischen
Wahrscheinlichkeitsbegriff (vgl. Der axiomatischen Wahrscheinlichkeitsbegriff II) erlernen.
Allerdings wird der Schritt, die theoretischen Wahrscheinlichkeitsverteilungen mit gewissen
Kennwerten zu beschreiben, durch die Verbindung zur Datenanalyse vorbereitet. 216 Dabei
ist es wichtig, die damit verbundene Unsicherheit zu verdeutlichen. Nur so kann der axiomatische Aufbau und der Übergang von der Binomialverteilung zur Normalverteilung (Zentraler Grenzwertsatz) verstanden werden.217
Die nächste Aufgabe (Aufgabe 2) hat zum Ziel, dass die Schüler zum einen die Universalität
der Binomialverteilung erkennen, zum anderen aber auch weitere Verteilungen erfassen. Die
empirischen Häufigkeitsverteilungen und die Gleichverteilung sind den Schülern bereits bekannt. Allerdings können auch weitere Wahrscheinlichkeitsverteilungen aus den Zählprinzipien (vgl. Laplace-Wahrscheinlichkeitsbegriff II) entwickelt werden. Alle haben gemein,
dass sie sich auf diskrete Wahrscheinlichkeitsräume beziehen. Die Wahrscheinlichkeitsverteilungen spielen im weiteren Verlauf dieser Arbeit und im Lehrplan keine Rolle, sodass die
Schüler diese lediglich durch eine Internetrecherche entdecken sollen.
214
Eichler; Vogel: Leitidee Daten und Zufall, S. 206.
An dieser Stelle könnten weitere Kennwerte der Datenanalyse untersucht werden. So könnte beispielsweise
auch die stochastische Konvergenz der Mittelwerte zum Erwartungswert entdeckt werden (vgl. Arbeitsblatt
„Der axiomatische Wahrscheinlichkeitsbegriff II“). Die Arbeit konzentriert sich allerdings auf die Stärken und
Schwächen der Wahrscheinlichkeitsbegriffe. Wahrscheinlichkeitsverteilungen werden sozusagen als Hilfsmittel (für das Beweis des schwachen Gesetzes der großen Zahlen) bzw. als Exkurs angesehen.
216
Biehler: Denken in Verteilungen, S. 2.
217
Daneben ist dieser Übergang problematisch, weil nun kontinuierliche Wahrscheinlichkeitsräume betrachtet
werden. Vgl. Tietze; Klika; Wolpers: Didaktik des Mathematikunterrichts, S. 276.
215
56
In der dritten Aufgabe erhalten die Schüler ein Zitat aus dem Schulbuch „Neue Wege“, zu
dem sie Stellung nehmen sollen:
„Wenn ich nur einen Versuch mache, dann interessiert mich nicht die Wahrscheinlichkeit, ob der Versuch gelingt. Bei einem Versuch glückt dieser oder nicht. Die relative Häufigkeit, mit der der Versuch
bei einer sehr häufigen Versuchswiederholung gelingt, ist für einen Versuch unerheblich.“ 218
Durch die Betrachtung der relativen Häufigkeit wird ersichtlich, dass es sich um eine Wahrscheinlichkeitsbestimmung im Nachhinein handelt, die als Voraussage für weitere Versuche
dient. Somit kann der frequentistische Wahrscheinlichkeitsbegriff natürlich eine Aussage
über einzelne Ereignisse machen. Allerdings ist korrekt, dass bei einem einzigen Versuch
jedes Versuchsergebnis möglich ist. In einem solchen Fall kann nur eine bestmögliche Wette
abgeschlossen werden. Dagegen benötigt eine relativ sichere Wette große Versuchszahlen.219 Darüber hinaus zeigt das frequentistische Modell eine Schwäche bei nicht theoretisch
unendlich oft wiederholbaren Zufallsvorgängen, insbesondere mit nur einmal durchführbaren Experimenten. Vielleicht spielt das Zitat auf diese Eigenart des frequentistischen Wahrscheinlichkeitsbegriffs an, mit dem diese Form von Zufallsexperimenten nicht behandelt
werden können. An dieser Stelle muss der subjektive Wahrscheinlichkeitsbegriff in Betracht
gezogen werden. Das Zitat ermöglicht die Reflexion der Chancen und Risiken des frequentistischen Wahrscheinlichkeitsbegriffs, die die Schüler in der Tabelle auf dem Arbeitsblatt
„Einstieg in die Stochastik“ ergänzen.
3.4 Der subjektive Wahrscheinlichkeitsbegriff
3.4.1 Arbeitsblatt I - Die bedingte Wahrscheinlichkeit
Das Problem des einmaligen Versuches und der Aspekt der Unabhängigkeit von Ereignissen
als notwendige Voraussetzung machen die Grenzen des frequentistischen Wahrscheinlichkeitsbegriffs deutlich. Diese können durch den subjektiven Wahrscheinlichkeitsbegriffs behoben werden. Der subjektive Wahrscheinlichkeitsbegriff bzw. die bedingte Wahrscheinlichkeit wird im Lehrplan eher als Exkurs gesehen. Dieser Meinung folgt diese Arbeit nicht,
da entscheidende Sätze wie die Pfadregeln auf diesem Wahrscheinlichkeitsbegriff aufbauen.
Außerdem ist jede Wahrscheinlichkeit eine bedingte Wahrscheinlichkeit, da sie von Vorinformationen abhängig ist.220 Allerdings sollte der Begriff der bedingten Wahrscheinlichkeit
218
Lergenmüller: Neue Wege, S. 30.
Hussmann; Prediger: Je größer, S. 29.
Schnell; Prediger: From “everything changes”, S. 825.
220
Malle; Malle: Was soll man, S. 53.
219
57
nicht überbetont werden, wie es beispielsweise Wickmann fordert.221 Die Unabhängigkeitsannahme spielt dafür in der Entwicklung der Wahrscheinlichkeitstheorie eine große Rolle.
Die Wahrscheinlichkeitsbegriffe sollten gleichberechtigt entwickelt werden, damit die Schüler beispielsweise bei Hypothesenentscheidungen (angedeutet in Aufgabe 3 des Arbeitsblattes „Subjektiver Wahrscheinlichkeitsbegriff II) das jeweils sinnvollere Wahrscheinlichkeitsmodell anwenden können.222
Um den subjektiven Wahrscheinlichkeitsbegriff einzuführen, wird als erste Aufgabe dieses
Arbeitsblattes auf die bekannten Zufallsgeneratoren des Würfels und des Riemer-Quaders
zurückgegriffen. Für beide „Würfel“ wurden auf dem Arbeitsblatt „Einstieg in die Stochastik“ mögliche Schätzungen für die Wahrscheinlichkeiten abgegeben (vgl. Tabelle 5):
Tabelle 5: Wahrscheinlichkeitsverteilungen Würfel und Quader.
Augenzahl
Wahrscheinlichkeit
Würfel
Wahrscheinlichkeit
Quader
1
1
6
0,05
2
1
6
0,1
3
1
6
0,35
4
1
6
0,35
5
1
6
0,1
6
1
6
0,05
Quelle: Eichler; Vogel: Leitidee Daten und Zufall, S. 166.
Ein Schüler übernimmt die Spielleitung und wählt entweder den Würfel oder den Quader
aus. Die restlichen Schüler sollen einschätzen, mit welcher Wahrscheinlichkeit, welcher
Würfel ausgewählt wurde. Diese Situation ist typisch für den subjektiven Wahrscheinlichkeitsbegriff, da das Ergebnis zum Zeitpunkt der Wahrscheinlichkeitsrechnung bereits feststeht.223 Hier wird die Unsicherheit des Individuums mit stochastischen Methoden beschrieben, was einen entscheidenden Unterschied zu den „objektiven“ Wahrscheinlichkeitsbegriffen darstellt, bei denen das Ergebnis prinzipiell nicht vorhersagbar ist.224
Die Schüler können über das Laplace-Modell argumentieren und die Wahrscheinlichkeit für
die beiden Zufallsgeneratoren mit
1
2
einschätzen. Allerdings können auch für Einschätzung
der Wahrscheinlichkeit für die Wahl des Würfels oder des Quaders subjektive Eindrücke
entscheidend sein. Beispielsweise kann das Argument angeführt werden, dass der Quaderwürfel der interessantere Zufallsgenerator ist und deshalb wahrscheinlicher ausgewählt
wurde. Auch kann das Argument umgedreht werden, sodass eher der bekannte Zufallsgenerator ausgewählt wurde. Dieses Vorgehen ist typisch für den subjektiven Wahrscheinlich-
221
Wickmann: Bayes-Statistik, S. X.
Borovcnik; Bentz; Kapadia: A Probabilistic Perspektiv, S. 44.
223
Eichler: Was ist Wahrscheinlichkeit, S. 70.
224
Götz; Humenberger: Problem des anderen, S. 55.
222
58
keitsbegriff. Es wird viel stärker mit Vergleichen („das eine ist wahrscheinlicher als das andere“) argumentiert, die vor allem im Alltag wiederzufinden sind. An dieser Stelle könnte
eine Wahrscheinlichkeitsskala unterstützend wirken, damit die Schüler numerische Werte
ihren Gefühlen zuordnen können. Somit wird auch deutlich, dass die subjektiven Eigenschaften ebenfalls die Eigenschaften der Nichtnegativität, Normiertheit, Additivität vorweisen müssen. Es wird deutlicher, warum Kolmogorov genau diese drei Eigenschaften als Axiome definierte.225
Des Weiteren kennen die Schüler die Schätzung von Wahrscheinlichkeiten vor dem Versuch
bereits vom Laplace-Modell. Dies verdeutlicht erneut die Schwäche des frequentistischen
Wahrscheinlichkeitsbegriffs, da Versuchsvorgänge immer in genügend großer Zahl durchgeführt werden mussten. Es hebt aber auch hervor, dass im Laplace-Modell nur die Schätzung der Gleichwahrscheinlichkeit möglich ist und diese nicht mehr auf Grund von Daten
modifiziert werden kann. Dieser Aspekt wird in der nächsten Aufgabe aufgegriffen, da auf
Grund eines Wurfes des Spielleiters die a priori-Wahrscheinlichkeit abgeändert werden soll.
Hierbei hilft die in der Einstiegsaufgabe erstellte Schätzung für die beiden Zufallsgeneratoren (vgl. Tabelle 5). An dieser Stelle sind vom Prinzip drei unterschiedliche Würfelergebnisse möglich:
1.
2.
3.
Es fällt eine 1 oder eine 6: Die Wahrscheinlichkeit, dass eine 1 oder eine 6 fällt, ist beim Quader
(0,05) viel unwahrscheinlicher als beim Würfel. Daher verändert sich die a priori Wahrscheinlichkeit nach der Verarbeitung der Informationen zugunsten des gewöhnlichen Würfels.
Es fällt eine 2 oder eine 5: Auch in diesem Fall ist die Wahrscheinlichkeit für den Würfel höher als
für den Quader. Allerdings unterscheiden sich die Wahrscheinlichkeiten kaum. Diese Information
veranlasst die Schüler ihre Anfangsprognose leicht in Richtung des gewöhnlichen Würfels zu verändern.
Es fällt eine 3 oder eine 4: Hier ist die Wahrscheinlichkeit, dass mit dem Quader geworfen wurde
1
(0,35) höher als mit dem Würfel ( ), das heißt die Information begünstigt die Wahrscheinlichkeit
für den Quaderwürfel. 226
6
Die Schüler erkennen so, dass die a priori-Wahrscheinlichkeiten auf Grund von Daten
manchmal verändert werden müssen. Analog zum frequentistischen Wahrscheinlichkeitsbegriff kann diese veränderte Wahrscheinlichkeit durch den Begriff a posteriori charakterisiert
werden. Dadurch wird deutlich, dass der subjektive Wahrscheinlichkeitsbegriff erst mit
mehrstufigen Zufallsexperimenten einen mathematischen Sinn erhält.227 Natürlich kann dieses Verfahren so oft wie gewünscht durchgeführt werden. Dazu wird die ermittelte a posteriori Wahrscheinlichkeit zur a priori Wahrscheinlichkeit modelliert und mit Hilfe von Würfen weitere a posteriori Wahrscheinlichkeiten bestimmt. Dadurch entsteht ein Schema, das
225
Eichler; Vogel: Leitidee Daten und Zufall, S. 166.
Ebd. S. 166.
227
Ebd. S. 116.
226
59
durch den Begriff des „Begünstigens“ geprägt ist. Das bedeutet, dass die Daten entweder
den Würfel oder den Quader begünstigen. Diese Vorstellung hilft beim Erkennen von bedingten Wahrscheinlichkeiten.228
Außerdem wird deutlich, dass die erste Einschätzung der Wahrscheinlichkeit durch die
Schüler, bei der noch keine Daten Einfluss genommen haben, im Laufe des Prozesses immer
unwichtiger werden. Die auf diese Art bestimmten Wahrscheinlichkeiten nähern sich immer
stärker auf Grundlage des empirischen Gesetzes der großen Zahlen den erhobenen Daten an.
Der frequentistische Wahrscheinlichkeitsbegriff hat daher bei großen Versuchszahlen gegenüber dem subjektiven Wahrscheinlichkeitsbegriff den Vorteil, dass die Wahrscheinlichkeiten nicht prozesshaft entstehen, sondern direkt aus den relativen Häufigkeiten übernommen werden können. Dies bedeutet aber auch, dass sich die Unsicherheiten (genügend große
Versuchszahlen und Stabilisation) auf den subjektiven Wahrscheinlichkeitsbegriff vererben.229
In Aufgabe 2 soll mit Hilfe der bereits bekannten Wahrscheinlichkeitsbegriffe das Begünstigen-Konzept quantifiziert werden. Dabei dürfen sich die Schüler aussuchen, mit welchem
Modell (Laplace und frequentistischen Modell) sie arbeiten wollen. Der zentrale Punkt zur
Begriffsbildung der bedingten Wahrscheinlichkeit ist die Reduktion des Wahrscheinlichkeitsraumes, der vom gewählten Modell unabhängig ist.230
In der ersten Gruppe wird erneut das Zufallsexperiment „Summe zweier Würfel“ (ein roter
und ein grüner Würfel) im Laplace-Modell betrachtet. Die Schüler berechnen zunächst die
Wahrscheinlichkeit, dass die Augensumme größer als 9 ist. Diese haben die Schüler bereits
6
in Aufgabe 2 des Arbeitsblattes „Der Laplace-Wahrscheinlichkeitsbegriff I“ mit 36 ermittelt.
Im Aufgabenteil b) ist die Augenzahl des grünen Würfels (6) bekannt. Die Schüler sollen
unter Berücksichtigung dieser Information wiederum die Wahrscheinlichkeit, dass die Augensumme größer als 9 zeigt, berechnen. In diesem Fall reduziert sich die Ergebnismenge
auf sechs Elementarereignisse, von denen drei (nämlich 4, 5, 6) günstig sind. Die Wahr3
scheinlichkeit kann also durch Abzählstrategien bestimmt werden und beträgt 6. Analog
kann in Aufgabeteil c) die Wahrscheinlichkeit für die Augensumme größer als 9 berechnet
3
werden, wenn bekannt ist, dass der grüne Würfel eine Augenzahl kleiner als 6 zeigt (30).
228
Borovcnik: Stochastik im Wechselspiel, S. 197.
Eichler; Vogel: Leitidee Daten und Zufall, S. 167.
230
Buth: Methodische Anregungen, S. 391.
229
60
Diese errechneten Wahrscheinlichkeiten werden als bedingte Wahrscheinlichkeit P(A|B)
bzw. PB(A), was „P von A unter der Bedingung B“ gelesen wird, bezeichnet.231
Die Schüler können durch weitere Beispiele erkennen, dass sie die Wahrscheinlichkeit mit
Hilfe des natürlichen Häufigkeitskonzepts durch P(A|B) = PB(A) =
Gegebenenfalls kann dies durch die Darstellung P(A|B) =
|A ∩ B|
|B|
P(A ∩ B)
P(B)
berechnen können.
erweitert werden. Dies
stellt keine Notwendigkeit dar, da sich die Nenner von P(A∩B) und P(B) gegenseitig wegkürzen. Allerdings sollte dies thematisiert werden, damit der Zusammenhang zur Pfadregel
deutlich wird. Die Schüler können die bedingten Wahrscheinlichkeiten also stets auf das
Modell der natürlichen Häufigkeit transferieren, indem sie sich eine große Versuchszahl N
vorstellen, mit der sie die angegebenen Werte (oft Prozente) multiplizieren.232 Diese Vorgehensweise stellt ein ideales Modell dar, wie es von A. Engel gefordert wurde.233 Außerdem
sollen die Schüler die Vor- und Nachteile der Repräsentationsformen „relative Häufigkeiten“ und „Brüche als Äquivalenzklassen“ an dieser Stelle erneut reflektieren.234
Ebenso kann die gleiche Vorgehensweise im frequentistischen Modell angewandt werden,
indem zunächst die relativen Häufigkeiten bestimmt werden. Sie können das Verfahren dann
analog auf Wahrscheinlichkeiten übertragen. Dabei wird davon ausgegangen, dass sich die
relativen Häufigkeiten auf Grundlage des empirischen Gesetzes der großen Zahlen stabilisieren. Im Endeffekt kann die bedingte relative Häufigkeit bzw. die bedingte Wahrscheinlichkeit wie im Laplace-Modell die durch P(A|B) = PB(A) =
|A ∩ B|
|B|
=
P(A ∩ B)
P(B)
berechnet wer-
den.235
Im Folgenden wird die Formel P(A|B) = PB(A) =
|A ∩ B|
|B|
=
P(A ∩ B)
P(B)
als die Definition der be-
dingten Wahrscheinlichkeit behandelt. Die Schüler erkennen durch die einfache Umformulierung P(A∩B)= P(B) ∙ P(A|B) die Pfadmultiplikationsregel. Außerdem wird der Zusammenhang zur Unabhängigkeit von Ereignissen deutlich. Sind die Ereignisse nämlich unabhängig, können die Schüler P(A∩B) als P(A)∙P(B) darstellen, sodass P(A) = P(A|B) darstellt.
Dies entspricht der intuitiven Vorstellung, dass B keinen Einfluss auf A hat. Die Definition
der bedingten Wahrscheinlichkeit und auch die Multiplikationspfadregel sind ebenfalls Modelle, die unsere Intuitionen ausdrücken sollen.236
231
Kütting; Sauer; Padberg: Elementare Stochastik, S. 170.
Wassner; Biehler; Martignon: Das Konzept, S. 40.
233
Engel: Wahrscheinlichkeitstheorie und Statistik.
234
Kütting; Sauer; Padberg: Elementare Stochastik, S. 170.
235
Ebd. S. 172.
236
Büchter; Henn: Elementare Stochastik, S. 217.
232
61
In der dritten Aufgabe des Arbeitsblattes beschäftigen sich die Schüler mit einem Aidstest.
Das Hauptaugenmerk soll hierbei auf den beiden Fehlertypen liegen, die beim Aids-Test
auftreten können. Bei der Modellierung dieses zweistufigen „Zufallsexperimentes“ mit Hilfe
des Baumdiagramms gibt es vier Pfade, von denen zwei einen Fehler des Aidstests symbolisieren. Die Schüler sollen in der Aufgabe die Wahrscheinlichkeit für die HIV-Erkrankung
unter der Bedingung eines positiven Aidstests ermitteln. Dabei kann der Satz von Bayes im
Modellierungsbereich der bedingten Wahrscheinlichkeit entdeckt werden. In der Aufgabe 3
wird zunächst angenommen, dass alle Menschen in Nordrhein-Westfalen getestet werden
und alle eine gleich hohe Wahrscheinlichkeit für eine Aids-Erkrankung besitzen.Erst im
Aufgabenteil b) wird diese Modellierung hinterfragt und in der ersten Aufgabe des nächsten
Arbeitsblatts (Der subjektive Wahrscheinlichkeitsbegriff II) aufgegriffen.237
In Aufgabenteil 3a) wird einer beliebigen Person aus Nordrhein-Westfalen wird mitgeteilt,
dass ihr Aids-Test positiv ist. Die Schüler sollen intuitiv schätzen, wie wahrscheinlich es ist,
dass sie tatsächlich an HIV erkrankt ist. Diese Schätzungen orientieren sich sehr stark an den
hohen Werten für die Sensitivität (richtig-positiv Rate von 99,9%) und die Spezifität (richtig-negativ Rate von (99,7%) und fallen daher oft viel zu hoch aus (oft zwischen 70-90%).238
Im nächsten Aufgabenteil (b) sollen die Schüler eine Vierfeldertafel erstellen, in der sie sowohl die absoluten als auch die relativen Häufigkeiten aus dem Artikel ermitteln (vgl. Tabelle 6).
Tabelle 6: Vierfeldertafel HIV-Erkrankungen.
Test positiv
Test negativ
Gesamt
Erkrankt
8991
8991
18000000
9
9
18000000
9000
9000
18000000
nicht erkrankt
53973
53973
18000000
17937027
17937027
18000000
17991000
17991000
18000000
Gesamt
62964
62964
18000000
17937036
17937036
18000000
18000000
18000000
18000000
Quelle: Eigene Konzeption.
Den Schülern kann bewusst werden, dass zwei Arten von Fehlern beim Aids-Test vorkommen können: Zum einen kann er positiv ausfallen, obwohl die Person nicht erkrankt ist und
zum anderen kann er negativ ausfallen, obwohl die Person erkrankt ist. An dieser Stelle kann
Biehler: Gesetze, S. 14.
237
Wassner; Biehler; Scheynoch: Authentisches Bewerten, S. 4.
Wassner; Biehler; Martignon: Das Konzept, S. 41.
238
Vgl. Kapitel „Sind Menschen gute Statistiker“ und Büchter: (Lebens-)gefährliche Trugschlüsse, S. 129.
62
also die Begriffsbildung des Fehlers erster und zweiter Art erfolgen und gegebenenfalls die
Begriffe Sensitivität und Spezifität eines Testes eingeführt werden.239
Im Folgenden berechnen die Schüler die in a) gesuchte Wahrscheinlichkeit.240 Dabei gibt es
aus mathematischer Sicht zwei sinnvolle Lösungswege. Die Schüler, die sich an die Aufgabe
2 dieses Arbeitsblattes erinnern, werden das Baumdiagramm über die absoluten Häufigkeiten erstellen (vgl. Abbildung 12):
Abbildung 12: Baumdiagram HIV-Erkrankung (absolute Häufigkeiten).
Quelle: Wassner; Biehler; Schweynoch, : Authentisches Bewerten, S. 4
Allerdings wird voraussichtlich die Mehrzahl der Schüler mit den relativen Häufigkeiten
arbeiten, weil sie dies bisher im Bereich des Baumdiagramms öfter durchgeführt haben(vgl.
Abbildung 13).
Abbildung 13: Baumdiagramm HIV-Erkrankung (relative Häufigkeiten).
1
0,0005
0,0004995
0,9995
0,0000001
0,0029985
0,9965015
Quelle: Eigene Konzeption.
Beide Modellierungen wurden durch die Vierfeldertafel in Aufgabenteil 3b) vorbereitet.
Durch das natürliche Häufigkeitskonzept können die Schwierigkeiten mit Prozenten oder
239
Pinkernell: Test positiv, S. 51.
Vor allem Bea präferiert bei der Berechnung der Wahrscheinlichkeiten an Stelle des Baumdiagramms das
Einheitsquadrat. Dieses hat den Vorteil, dass die Wahrscheinlichkeiten sich geometrisch durch einen Flächenvergleich abbilden. Vgl. Bea: Stochastisches Denken, S. 154.
Fischer: Stochastik einmal anders, S. 99.
In dieser Arbeit wurde sich trotzdem für das Baumdiagramm entschieden, da es sowohl den prädikativen als
auch den funktionalen Lerntyp abdeckt und bereits vorher verwendet wurde (Sequenzargument). Außerdem ist
das Baumdiagramm universell einsetzbar. Vgl. Krauss: Wahrscheinlichkeit und Intuition, S. 144.
240
63
Brüchen umgangen und die Darstellung formal vereinfacht werden.241 Außerdem setzen die
Schüler nicht mehr routinemäßige in die Formel ein, da sie erklären müssen, wie sie die
Situation modelliert haben.242 Der einzige Nachteil dieser Darstellung ist, dass die Knoten
des Baumdiagramms immer natürliche Zahlen darstellen müssen. Dies ist in einigen Situationen unrealistisch, sodass auch das Baumdiagramm mit den relativen Häufigkeiten zur Bezugsgröße 1 verwendet werden soll.243
Aus den Baumdiagrammen können die Schüler nun die gewünschte Wahrscheinlichkeit berechnen: P(erkrankt| Test positiv) =
|erkrankt ∩ Test postiv|
|Test positiv|
8991
8991
= 8991+53973 = 62964 = 14,28%. Das
gleiche Ergebnis erhält man auch bei der Verwendung von relativen Häufigkeiten bzw. Brüchen als Repräsentanten einer Äquivalenzklasse. Die Schüler können so den Satz von Bayes
entdecken:
P(B|A) =
|B ∩ A|
|A|
=
P(B) ∙ P(A|B)
̅ ) ∙ P(A|B
̅)
P(B)∙P(A|B) + P(B
=
P(B) ∙ P(A|B)
P(A)
.
In Worten ausgedrückt bedeutet dies: „Die Wahrscheinlichkeit, dass ein Ereignis über einen bestimmten Pfad eintritt, ist gleich dem Quotienten aus der Wahrscheinlichkeit dieses Pfades und der Summe
der Wahrscheinlichkeiten aller Pfade, die zu dem Ereignis gehören.“ 244
P(B) ∙ P(A|B)
Die Schüler erkennen vor allem am Term P(B) ∙ P(A|B) +P(B̅) ∙ P(A|B̅) die enge Verbindung zwischen dem Satz von Bayes und der Definition der bedingten Wahrscheinlichkeit. Ebenso wie
die Multiplikationspfadregel lässt sich der Satz von Bayes durch die Anwendung der Definition der bedingten Wahrscheinlichkeit beweisen: P(B|A)=
P(A ∩ B)
P(A ∩ B)
∙ P(B)
P(B)
P(A)
P(A)
=
P(A|B) ∙ P(B)
=
P(A)
.
Daher wird der Satz von Bayes auch manchmal als dritte Pfadregel bezeichnet.245
Der letzte Aufgabenteil (d) hinterfragt die Modellannahme, indem die Bedeutung der sogenannten Basisrate von 7,8% analysiert wird. Dies wird mit dem Begriff „Modell-RealitätRückkopplungsargument“246 bezeichnet, das in stochastischen Modellbildungsprozessen
eine zentrale Rolle einnimmt. Auf der einen Seite ist es nicht sinnvoll, dass alle Menschen
einen Aids-Test machen. So würde bei einem großen Teil der Menschen fälschlicherweise
Aids diagnostiziert werden, was furchterregende Konsequenzen für das Leben der betroffenen Personen hätte. So existieren Fallbeispiele, in denen Personen, die falsch-positiv getestet
241
Büchter; Henn: Elementare Stochastik, S. 129.
Wassner; Biehler; Martignon: Das Konzept, S. 39.
Krauss: Wie man das, S. 5.
243
Eichler; Vogel: Leitidee Daten und Zufall, S. 208.
244
Büchter; Henn: Elementare Stochastik, S. 216.
245
Ebd. 217.
Fischer: Stochastik einmal anders, S. 105.
246
Krauss: Wahrscheinlichkeit und Intuition, S. 143.
242
64
wurden, ihre komplette Existenz verloren haben und Selbstmord begingen. Natürlich gibt es
aber auch Risikogruppen wie Drogensüchtige, bei denen ein Aids-Test sinnvoll ist. Bei diesen Gruppen verändert sich die Basisrate. Daher soll in Aufgabe 1 des folgenden Arbeitsblattes die Auswirkung der Basisrate auf die Fehlertypen untersucht werden. 247
Auf der anderen Seite stellt der Aidstest einen Informationsgewinn dar, der sich schrittweise
durch den Satz von Bayes vollzieht. Daher wird in der Vertiefung die erste Aufgabe dieses
Arbeitsblattes erneut betrachtet und die Ergebnisse quantitativ analysiert. Die Schüler erfahren auf diese Weise, was es im mathematischen Sinne bedeutet durch Informationen bzw.
Indizien zu lernen. Es wird deutlich, dass der Satz von Bayes oftmals in Situationen angewandt wird, die mit dem frequentistischen Wahrscheinlichkeitsbegriff nicht erfasst werden
können. Mit dem frequentistischen Wahrscheinlichkeitsbegriff kann beispielsweise nicht erfasst werden, welcher Würfel gewählt wurde oder ob eine bestimmte Person an HIV erkrankt
ist.248
3.4.2 Arbeitsblatt II - Die Basisrate
In der ersten Aufgabe des zweiten Arbeitsblattes zum subjektiven Wahrscheinlichkeitsbegriff wird die Basisrate untersucht. Im ersten Aufgabenteil berechnen die Schüler für Risikogruppen eine Wahrscheinlichkeit für einen falsch-positiven Aids-Test.249 Dafür benutzen
sie wieder den Satz von Bayes und erhalten schließlich als Ergebnis
847
847 + 20
=
847
, also
867
97,69%. Es gibt zwar immer noch Fälle, in denen ein falsch-positives Ergebnis zustande
kommt, allerdings sind diese viel weniger. Dies liegt an der höheren Basisrate (11,3%).
Diese Tatsache lässt sich auf jede Umfrage übertragen, da es eine große Rolle spielt, welche
Personengruppe befragt wurde. Den Schülern soll so bewusst werden, welchen großen Einfluss die Stichprobe einnimmt. Aus diesem Grund ist die Frage nach dem Zustandekommen
der Informationen bzw. der Daten für die Aussagekraft der Umfrage essentiell.250
Der große Einfluss der Basisrate auf das Ergebnis wird auch im Aufgabenteil b) deutlich
(vgl. Abbildung 14). In diesem sollen die Schüler einen Funktionsgraphen für eine Stadt mit
100.000 Einwohnern erstellen. Durch die Nennung der Einwohnerzahl soll das natürliche
Häufigkeitskonzept offen gehalten werden. Hier ist es aber sinnvoller mit relativen Häufigkeiten bzw. Brüchen zu arbeiten, um einen Verallgemeinerungscharakter zu erzielen. Die
Schüler bemerken so intuitiv, dass es sich bei der Sensitivität, Spezifität und den Fehlern
247
Wassner; Biehler; Schweynoch: Authentisches Bewerten, S. 10.
Eichler; Vogel: Elementare Stochastik, S. 200.
249
Israel: Was hat Aids, S. 104.
250
Götz; Humenberger: Das Problem, S. 53.
248
65
erster und zweiter Art um bedingte Wahrscheinlichkeiten handelt, da sie von der Basisrate
abhängen.251
Abbildung 14: Basisrate.
Quelle: Eigene Konzeption.
Die zweite Aufgabe des Aufgabenblattes ist als Stationenlernen konzipiert worden. Alle Stationen (das Taxiproblem, das Ziegenproblem252, das Kästchenparadoxon Bertrands253, Gerichtsverhandlung254) wurden bereits auf dem einleitenden Arbeitsblatt „Sind Menschen
gute Statistiker?“ behandelt. Auf diesem schätzten die Schüler ohne wahrscheinlichkeitstheoretische Kenntnisse die Wahrscheinlichkeit für die jeweilige Problemstellung.255 Nun werden diese von den Schülern überprüft. Zum einen wird durch das Stationenlernen deutlich,
dass die bedingte Wahrscheinlichkeit in vielen Bereichen zu intuitiven Fehlschlüssen führt
und dass es kein Problem darstellt, Fehler zu machen. Eine Reflexion der Situation kann
helfen, um rationale Entscheidungen unter Unsicherheit zu treffen. Die Lehrkraft soll die
Schüler lediglich bei mathematischen Fragestellungen unterstützen. Es darf nicht der Eindruck entstehen, dass sie bei Fehlschlüssen versagt haben. Vielmehr muss der Lernprozess
betont und deutlich gemacht werden, dass man sich in stochastischen Fragestellungen nicht
allzu sehr auf die Intuition verlassen kann.
251
Darüber hinaus kann untersucht werden, wie sich der Graph ändert, wenn die Spezifität und Sensitivität des
Tests geändert werden. Vgl. Wassner; Biehler; Schweynoch: Authentisches Bewerten, S. 10.
252
Zimmermann; Gundlach: Wie Ziegen, S. 316.
253
Bartz: Denkfallen vermeiden, S. 32.
254
Schrade: Schwierigkeiten, S. 88.
Krauss: Eignet sich die Formel, S. 123.
255
Für eine Analyse der Aufgaben vgl. Kapitel 2 „Sind Menschen gute Statistiker?“.
66
In Aufgabe 3 sollen die Stärken und Schwächen des subjektiven Wahrscheinlichkeitsbegriffs
deutlich werden. Dazu wird ein Vergleich der unterschiedlichen Vorgehensweisen des subjektiven und des frequentistischen Wahrscheinlichkeitsbegriffs bei der Hypothesenüberprüfung durchgeführt. Dieser Aufgabenteil bereitet daher die beurteilende Statistik vor. Dabei
ist es wichtig, dass der Begriff des Hypothesentests bereits beim Satz vom Bayes im Vordergrund steht und nicht erst losgelöst von den bedingten Wahrscheinlichkeiten beim Signifikanztest eingeführt wird. Außerdem sollte betont werden, dass der Signifikanztest bedingte
Wahrscheinlichkeiten verwendet. Durch eine Gegenüberstellung der beiden Arten des Hypothesentests kann der oft geforderte Methodenpluralismus erreicht werden.256
Zunächst betrachten die Schüler dazu, wie sie über die Hypothese in der Aufgabe „Warum
gibt es immer so wenige rote Gummibärchen in der Tüte?“ entschieden haben. Ihnen wird
bewusst, dass sie zunächst eine Hypothese aufgestellt haben, die zum Beispiel aus dem Laplace-Ansatz entstanden ist. In der Folge sammelten sie möglichst viele Daten, um danach
über die Hypothese zu entscheiden. Mathematisch gesehen ging es hierbei um die Beurteilung der bedingten Wahrscheinlichkeit P(relative Häufigkeit der roten Gummibärchen|
Gleichwahrscheinlichkeitsverteilung der Gummibärchen). Wann und ob die Hypothese verworfen wird, war jeder Versuchsperson selbst überlassen. In der Wissenschaft wird fast
durchgängig das sogenannte Signifikanzniveau von 5% verwendet.257 Es wird eine bedingte
Wahrscheinlichkeit nach Durchführung von möglichst vielen Versuchen berechnet, wobei
die einzelnen Versuche unabhängig sein müssen.258
Der subjektive Wahrscheinlichkeitsbegriff bzw. der Satz von Bayes geht entgegengesetzt
vor. Es wird von einer subjektiven Wahrscheinlichkeit a priori ausgegangen, die schrittweise
mit Daten verändert wird (a posteriori Wahrscheinlichkeit). Somit wird mit Hilfe des Satzes
von Bayes die bedingte Wahrscheinlichkeit P(Gleichwahrscheinlichkeitsverteilung der
Gummibärchen| relative Häufigkeit der roten Gummibärchen) verwendet. Das bedeutet, dass
„die Wahrscheinlichkeit, dass die Hypothese zutrifft unter Voraussetzung der Information,
die unter Berücksichtigung einer a-priori-Wahrscheinlichkeit für die Hypothese durch das
256
Ziel der Arbeit ist es nicht die Hypothesentests zu entwickeln, sondern lediglich das unterschiedliche Vorgehen zu verdeutlichen. Vgl. Krauss; Wassner: Wie man das, S. 33.
257
Durch diese Vorbereitung könnten viele Schwächen bei der Interpretation des Signifikanzniveaus vorgebeugt werden. Vgl. Birnbaum: Interpretation statistischer Signifikanz, S. 42.
Spandaw: Was bedeutet, S. 42.
258
Eichler; Vogel: Leitidee Daten und Zufall, S. 206.
Wickmann: Bayes- Statistik, S. 154.
67
Stichprobenergebnis zustande gekommen ist.“259 Daher muss im subjektiven Wahrscheinlichkeitsmodell jede Wahrscheinlichkeit neu interpretiert werden, eine Bestätigung der Vermutung gibt es nicht.260
Obwohl aus algebraischer Sicht beide Vorgehensweisen korrekt sind, ist in der Mathematik
und auch in der Didaktik deswegen ein Streit entbrannt. Die Verfechter des frequentistischen
Ansatzes werfen den Subjektivisten einen unwissenschaftlichen Ansatzpunkt vor, da eine
subjektive Meinung Einfluss auf die Ergebnisse hat. Hingegen betonen die Bayesianer die
subjektiven Einflüsse im Bereich des frequentistischen Ansatzes. So stellt beispielsweise das
Signifikanzniveau aus der Sicht der Subjektivisten eine beliebige Setzung dar. Letztendlich
kann man festhalten, dass beide Ansätze ihre Stärken und Schwächen besitzen, die aus den
verschiedenen Wahrscheinlichkeitsbegriffen folgen. Als Unterscheidungsmerkmal kann laut
Wickmann die Charakterisierung „objektive Wahrscheinlichkeiten sind fest, aber unbekannt“ und „subjektive Wahrscheinlichkeit sind veränderlich, aber bekannt“ verwendet werden.261 Es ist somit eine Frage der Modellbildung, welcher Hypothesentest verwendet
wird.262 Damit die Schüler für die Realität jedoch ein adäquates Modell finden können, müssen den Schülern die stochastischen Denkweisen bewusst sein sowie mehrere Modelle zur
Auswahl stehen.263 Allerdings bedeutet dies auch, dass die stochastische Theorie umfassend
zu bearbeiten ist. Beispielsweise würde die didaktische Reduzierung der stochastischen
Konvergenz die Unsicherheit beim frequentistischen Hypothesentest zu großen Teilen überdecken.264
Die letzte Aufgabe des Arbeitsblattes (Vertiefung) bildet den Abschluss der inhaltlichen
Wahrscheinlichkeitsbegriffe. Die Schüler sollen die Stärken und Schwächen der einzelnen
Wahrscheinlichkeitsmodelle reflektieren und die bereits erhaltene Tabelle ergänzen.265 Dabei werden ihnen auch Probleme bewusst, die mit Hilfe der inhaltlichen Wahrscheinlichkeitsbegriffe nicht gelöst werden konnten. Dazu zählen vor allem die Probleme des kontinuierlichen Wahrscheinlichkeitsraums, der stochastischen Konvergenz sowie insbesondere die
Beantwortung der Frage „Was sind Wahrscheinlichkeiten?“. Bisher lernten die Schüler nur
259
Eichler; Vogel: Leitidee Daten und Zufall, S. 206.
Gigerenzer; Krauss: Statistisches Denken, S. 60.
261
Wickmann: Zur Begriffsbildung, S.55.
262
Eichler; Vogel: Leitidee Daten und Zufall, S. 207.
Spandaw: Was bedeutet, S. 53.
Ausführliche Analyse in: Tschirk: Statistik: Klassisch oder Bayes.
263
Vascó: Parallel Discussion, 295.
264
Kütting: Stochastik im Matheunterricht, S. 11.
Wickmann: Der Theorieeintopf, S. 123.
265
Eine ausgefüllte Tabelle ist im Anhang zu finden.
260
68
die Berechnung von Wahrscheinlichkeiten und nicht was darunter verstanden wird. Die Herleitung des axiomatischen Wahrscheinlichkeitsbegriffs soll sich stark an diesen Problemen
orientieren. Währende der Bearbeitung der Arbeitsblätter können die Schüler die Stärken
und Schwächen des axiomatischen Zugangs erlernen, sodass die Wahrscheinlichkeitsbegriffe abschließend diskutiert werden können.
3.5 Der axiomatische Wahrscheinlichkeitsbegriff
3.5.1 Arbeitsblatt I - Die Axiomatik nach Kolmogorov
In Aufgabe 1 des Arbeitsblattes sollen die Schüler den axiomatischen mit den inhaltlichen
Wahrscheinlichkeitsbegriffen vergleichen. Ihnen wird bewusst, dass die Bindung an konkrete Situationen aufgegeben werden musste, um den Begriff Wahrscheinlichkeit zu definieren. Nichtsdestotrotz sollte die Wahrscheinlichkeitstheorie immer noch zur Beschreibung
der Realität verwendet werden. Kolmogorov stellte 1933 in seinem Werk „Grundbegriffe
der Wahrscheinlichkeitsrechnung“ seine Axiomatik vor. Vorbild hierfür ist Hilberts Vorstellung über die Geometrie. Auch er löste sich von den konkreten Vorstellungen und Definitionen (vor allem die Euklids) und legte formale Regeln fest, die für Punkte und Geraden
gelten sollten.266 Setzt man das Jahr 1654 als Geburt der Wahrscheinlichkeitsrechnung,
konnte erst knapp 300 Jahre später überhaupt definiert werden, was Wahrscheinlichkeiten
sind. Statt einer objektiven Wahrscheinlichkeit bzw. einer konkreten Anschauung, geht Kolmogorov von einer (un)endlichen267 Menge Ω und einer Teilmenge Ϝ der Potenzmenge P(Ω)
aus, deren Elementarelemente als zufällige Ereignisse bezeichnet werden. Für diese stellt
Kolmogorov Axiome auf. Das Axiomensystem sollte also „als Endstufe des genetischen
Prozesses“268 behandelt werden.
Dieses Axiomensystem stellt nur eine mögliche Form von Verknüpfungen dar und nicht die
Tatsache an sich. Anders ausgedrückt legen die Axiome fest, wie man mit Wahrscheinlichkeiten rechnen kann und nicht, was Wahrscheinlichkeiten sind.269 Erst im Nachhinein werden die konkreten Situationen interpretiert. Bisher wurde die konkrete Situation analysiert
und dort nach Regelmäßigkeiten gesucht.270 Man hat also sozusagen den „Spieß umgedreht“271.
266
Fischer; Lehner; Puchert: Einführung in die Stochastik, S. 77.
Die Schüler bekommen zunächst eine Definition für endliche Wahrscheinlichkeitsräume. Danach wird diese
in einer Art Ausblick auf unendliche Mengen erweitert.
268
Wittmann: Grundfragen des Mathematikunterrichts, S. 147.
269
Biehler; Engel: Stochastik, S. 224.
270
Ineichen: Modellbildung von Zufallsphänomenen, S. 48.
271
Fischer; Lehner; Puchert: Einführung in die Stochastik, S. 78.
267
69
Dennoch sind die Axiome nicht beliebig, sondern repräsentieren die Gemeinsamkeiten der
inhaltlichen Wahrscheinlichkeitsbegriffe, also Nichtnegativität, Additivität und Normiertheit. Damit spiegelt die Axiomatik die Eigenschaften der Laplace-Wahrscheinlichkeit, des
subjektiven Wahrscheinlichkeitsbegriffs und insbesondere der relativen Häufigkeiten wider.272 Im endlichen (und ähnlich im abzählbar unendlichen) Fall, in der die Potenzmenge
als Wahrscheinlichkeitsfeld verwendet werden kann,273 reichen diese drei Axiome für die
Wahrscheinlichkeitsverteilung P aus. Alle anderen Eigenschaften, die schon durch die inhaltlichen Wahrscheinlichkeitsbegriffe bekannt waren, lassen sich daraus herleiten.274
Die folgende Definition Kolmogorovs ist also effizient, widerspruchsfrei und valide275:
Ein Wahrscheinlichkeitsraum (Ω, P) ist ein Paar bestehend aus einer nichtleeren Menge Ω={ω1 , … , ωn }
und einer Funktion P: P(Ω)→ ℝ mit den Eigenschaften:
1) P(E) ≥0 für alle Teilmengen E von Ω (Nichtnegativität).
2) P(Ω) = 1 (Normiertheit).
3) P(E1∪E2) = für alle Teilmengen E1, E2 mit E1∩E2=Ø (Additivität).
Ω heißt Ergebnismenge, P(Ω) Ereignismenge, P Wahrscheinlichkeitsverteilung und P(E) Wahrscheinlichkeit des Ereignisses E.
Durch dieses Axiomensystem wird die Wahrscheinlichkeit als normiertes Maß276 definiert,
das heißt jedem Ereignis wird eine reelle Zahl mit den oben genannten Eigenschaften zugeordnet. Jedoch wird nicht beantwortet, wie die Zuordnung P(E) aussieht.277 Wahrscheinlichkeit muss also als ein theoretischer Begriff verstanden werden, der sich im Wahrscheinlichkeitskalkül entfaltet.278 Daher ist es notwendig, den formalen Aspekt der Stochastik zu betonen. Dieser wurde bisher zu Gunsten des Anwendungsaspekts bisher möglichst gering gehalten. Den Schülern wird somit klar, was mit dem Zusammenspiel von Theorie und Praxis
gemeint ist.279
Darüber hinaus beweisen die Schüler in Aufgabenteil 2b) die Eigenschaften einer Wahrscheinlichkeitsverteilung, die sie sowohl vom Laplace- als auch vom frequentistischen
Wahrscheinlichkeitsbegriff kennen, um den Umgang mit dem Axiomensystem zu üben und
mathematisch beweisen zu lernen:
- P(E) ≤ 1 für alle E ⊆ Ω .
- P(∅) = 0.
̅) = 1 − P(E) für alle E ⊆ Ω .
- P(E
272
Biehler: Gesetze, S. 17.
Im unendlichen Fall benötigt Kolmogorov die Maßtheorie.
274
Eichler; Vogel: Leitfaden Stochastik, S. 106.
275
Dörte: Mathe sehen, S. 263.
276
Wahrscheinlichkeiten können also wie physikalischen Größen gemessen werden, da die relative Häufigkeit
als gute Schätzgröße für die Wahrscheinlichkeit angesehen werden kann. Hierzu ist das Bernoulli‘sche Gesetz
der großen Zahlen nötig.
277
Barth: Abiturtraining, S. 37.
278
Dinges: Zum Wahrscheinlichkeitsbegriff, S. 61.
279
Eichler: Vorstellungen, S. 44.
Freudenthal: Mathematik als pädagogische Aufgabe, S. 535.
273
70
- P(E1 ∪ E2) = P(E1) + P(E2) − P(E1∩E2) für alle E1, E2 ⊆ Ω .
- Speziell gilt: P(E) = ∑ω∈E P({ω}) und P(Ω) = ∑ω∈Ω P({ω}) = ∑ni=1 P({ωi}) = 1.280
So erkennen die Schüler, dass es sich bei der Axiomatik um eine Mengendarstellung handelt.
Aus der Analysis kennen sie für Mengendarstellungen das Visualisierungswerkzeug des
Venn281-Diagramms. Bei der Verwendung muss darauf geachtet werden, dass nicht alle Situationen abgedeckt werden können (beispielsweise können disjunkte Mengen nicht dargestellt werden). Der Beweis über die Axiome deckt hingegen alle Fälle ab.282
Neben den Eigenschaften einer Wahrscheinlichkeitsverteilung sollen die Schüler auch den
Satz über die Festlegung einer Wahrscheinlichkeitsrechnung beweisen (Aufgabe 2b):
Ist Ω = {ω1, ω2,…, ωn} eine endliche Ergebnismenge, so ist eine Wahrscheinlichkeitsverteilung P durch
ihre Werte für die Elementarereignisse eindeutig festgelegt. Wird hierfür jedem ωi ∈ Ω eine Zahl
P({ωi}) ∈ [0; 1] zugeordnet, wobei ∑ni=1 P({ωi}) = 1 gilt und P(E) ∶= ∑ω∈E P({ω}), so ist P eine Wahrscheinlichkeitsverteilung von P. Die Umkehrung gilt ebenfalls. 283
An diesem Satz wird deutlich, dass die Festlegung einer Wahrscheinlichkeitsverteilung
durch die Kolmogorov Axiome und durch die Elementarereignisse äquivalent ist. Diese
Äquivalenz gilt allerdings bei (abzählbar) unendlichen Mengen nicht, wie in der nächsten
Aufgabe deutlich wird. Hier wird die Umgang mit einer Axiomatik deutlich: Da diese Äquivalenz für unsere Vorstellung elementar wichtig ist, wird ein neuer (inhaltlich wenig gefüllter) Begriff (Sigma-Additivität) definiert, unter dem diese Äquivalenz weiterhin gilt. Allerdings steht nicht die Definition der Sigma-Additivität im Vordergrund, sondern lediglich das
Verständnis, welche Probleme der Übergang von endlichen zu unendlichen Mengen mit sich
bringt.
Aufgabe 3 verdeutlicht diese Problematik. Die Schüler haben bereits gelernt, dass LaplaceWahrscheinlichkeiten bei abzählbar unendlichen Ergebnismengen nicht mehr berechnet
werden können. Stattdessen kann bei einer kontinuierlichen Menge durch eine Flächenbetrachtung ein Laplace-ähnlicher Zustand hergestellt werden. Anhand des Beispiels „Warten
auf den ersten Erfolg beim Glücksrad“ wird eine abzählbar unendliche Ergebnismenge betrachtet (Ω={1, 2, 3, …}). In dieser Ergebnismenge besitzen die Elementarereignisse nicht
9
1
10
10
die gleiche Wahrscheinlichkeit, sondern können über die Formel P(ωn) = ( )n-1 ∙
berech-
net werden. Damit eine Wahrscheinlichkeitsverteilung vorliegt, müssen sich die Wahrscheinlichkeiten der Elementarereignisse zu 1 aufsummieren, das heißt ∑∞
i=1 P(ωi) = 1.
280
Büchter; Henn: Elementare Stochastik, S. 185.
Diese sind nach dem englischen Geistlichen und Logiker John Venn benannt, wurden aber eigentlich von
Euler eigeführt.
282
Die Lösungen der Aufgabe 2 befinden sich im Anhang.
Bosch: Elementare Einführung, S. 12.
283
Ebd. S. 187.
281
71
Durch den Tipp, dass die Schüler die geometrische Summenformel anwenden sollen, be9
1
1
9
1
∞
∞
i-1
i
rechnen sie ∑∞
i=1 P(ωi) = ∑i=1(10) ∙ 10 = 10 ∙ ∑i=0(10) = 10 ∙
1
1−
9
10
= 1.284
Damit wird den Schülern im abzählbar unendlichen Fall ersichtlich, dass aus der Festlegung
einer Wahrscheinlichkeitsverteilung über die Elementarereignisse, die Kolmogorov-Axiome
geschlossen werden können. Allerdings gilt die Rückrichtung (Schluss von den Kolmogorov-Axiomen auf die Festlegung einer Wahrscheinlichkeitsverteilung über Elementarereignisse) nicht, sodass die erwähnte Sigma-Additivität eingeführt werden muss. Diese Information erhalten die Schüler in einem Info-Text. Eine ausführliche Begriffsbildung für die
Sigma-Additivität (bzw. der Sigma-Algebra) würde das Schulniveau überschreiten, sodass
es didaktisch reduziert wurde.285 Außerdem wird die Notwendigkeit der Verwendung einer
Mengenalgebra erst an dieser Stelle deutlich. Würde man sich auf endliche Ergebnismengen
konzentrieren, würde die Mengenalgebra überflüssig wirken.286
Der nächste Aufgabenteil (3b) behandelt die überabzählbar unendlichen Ergebnismengen.
Die Schüler wissen bereits, dass mit Hilfe des geometrischen Ansatzes, Wahrscheinlichkeiten berechnet werden können. Jedoch bleibt das Problem bestehen, dass die Wahrscheinlichkeitsverteilung nicht mehr über die Elementarereignisse und damit über die Potenzmenge
definiert werden kann. Ein Satz der Maßtheorie besagt nämlich, „dass es keine Funktion P
gibt, die im überabzählbaren Fall auf der Potenzmenge definiert ist, auf den einelementigen
Teilmengen den Wert 0 hat und die Axiome einer Wahrscheinlichkeitsverteilung erfüllt.“287
Da die Schüler nur endliche und selten abzählbar unendliche Problemstellungen lösen werden, wird die Erweiterung der Axiomatik (Ersetzung der Potenzmenge durch die Borel‘sche
Sigma-Algebra) didaktisch reduziert. Allerdings sollen die Schüler für die Probleme sensibilisiert werden, die beim Übergang von diskreten zu kontinuierlichen Mengen, wie beim
zentralen Grenzwertsatz, entstehen. Oftmals geht die Binomialverteilung sozusagen fließend
in eine stetige Funktion über. Dabei „verlieren“ die einzelnen diskreten Werte der Binomialverteilung jedoch ihre Wahrscheinlichkeiten. In kontinuierlichen Wahrscheinlichkeitsräu-
284
Ebd. S. 188.
Ebenfalls didaktisch reduziert wurde die Tatsache, dass die Wahrscheinlichkeitsverteilung weiterhin über
die Potenzmenge definiert wird. Für die Wohldefiniertheit benötigten die Schüler Kenntnisse über die absolute
Konvergenz von Summen. Vgl. Büchter; Henn: Elementare Stochastik, S. 187.
286
Schmidt: Schwächen, S. 21.
287
Büchter; Henn: Elementare Stochastik, S. 195.
285
72
men können die Wahrscheinlichkeiten nur über eine Flächenbetrachtung mittels (Lebesque288-) Integrale bestimmt werden.289
Des Weiteren sollen die Schüler in Aufgabenteil 3b) die Wahrscheinlichkeit berechnen, dass
die Gleichung x2 + ax + b = 0 mit a, b ≤ |1| eine Lösung besitzt, um die Teilbereiche Analysis
und Stochastik stärker miteinander zu verknüpfen. Dazu testen sie zunächst einige Werte für
a und b, um ein Gefühl für die Situation zu bekommen. Dieses Vorgehen kann verallgemeinert werden, indem sie die p-q-Formel nutzen bzw. quadratisch ergänzen und den Radikand
a
√−b + (2)² betrachten. Die Gleichung ist genau dann lösbar, wenn der Radikand ≥0 ist.
a²
Dies führt zur Funktion b(a) ≤ 4 , die als die Dichtefunktion bezeichnet werden kann. Folgendes Schaubild (vgl. Abbildung 15) verdeutlicht die Situation:
Abbildung 15: Lösung quadratische Funktion.
Quelle: Eigene Konzeption.
Die Schüler können den geometrischen Wahrscheinlichkeitsbegriff anwenden, den Punkten
1
unter der x-Achse die Wahrscheinlichkeit 2 zuweisen und mit Hilfe des Integrals die Fläche
1
1
unter dem Graphen mit 6 bestimmen. Anschließend berechnen die Schüler den Anteil von 6
vom gesamten Quadrat, also
1
6
2²
1
= 24. Dieses Vorgehen kennen sie bereits aus dem Laplace13
Ansatz. Die Gleichung ist also mit der Wahrscheinlichkeit von 24 lösbar. Hier wird erneut
deutlich, dass die Wahrscheinlichkeit für die Lösbarkeit eines einzelnen Punktes 0 beträgt.
Dies liegt daran, dass das Integral über einen Punkt den Wert 0 besitzt.
288
Mit Riemann-Integralen können nur Intervalle und keine Mengen berechnet werden. Daher wird das allgemeinere Lesbeque-Integral verwendet. Vgl. Ebd. S. 193.
289
Bender: Grundvorstellungen und Grundverständnisse, S.19.
73
Die Schüler sollen generell erkennen, dass die Axiomatik nach Kolmogorov sehr nah an den
inhaltlichen Wahrscheinlichkeitsbegriffen aufgebaut ist. Dies wird daran deutlich, dass die
Axiome lediglich Eigenschaften der inhaltlichen Wahrscheinlichkeitsbegriffe widerspiegeln. Entscheidend ist aber die Abkehr von der inhaltlichen Bindung, sodass definiert werden konnte, was Wahrscheinlichkeiten im mathematischen Sinne sind. Die Schüler müssen
daher bei der Betrachtung des Zufallsexperiments folgende Unterscheidungen eines Wahrscheinlichkeitsansatzes machen: Ihnen stellen sich die Fragen, ob das Experiment wiederholbar ist oder nicht, ob die Ergebnismenge endlich, abzählbar oder überabzählbar unendlich
ist und mit Hilfe welches Wahrscheinlichkeitsmodells die Wahrscheinlichkeitsansätze konkret gewonnen wurden.290
Gerade in der heutigen Zeit, in der die Bedeutung der Mathematik durch den Computereinsatz in Frage gestellt wird, ist es notwendig mathematische Grundfragen im Schulunterricht
zu behandeln. Ziel kann dabei nicht sein, die formalen Aspekte der Mathematik zu stark zu
fokussieren. Allerdings sollte den Schülern bewusst sein, warum diese Formalitäten Einzug
in die Mathematik erhalten haben. Die Betrachtung des Wahrscheinlichkeitsraumes und der
stochastischen Konvergenz sind Beispiele hierfür. Anhand inhaltlicher Problemstellungen
und Begründungen sollen die Schüler erfahren, warum in der Kolmogorov’schen Axiomatik
beispielsweise eine σ-Algebra eingeführt wurde. Eine Ausklammerung dieser mathematischen Grundlagenprobleme kann und darf nicht das Ziel eines Unterrichtes im Leistungskurs
sein.291
In der Vertiefung üben die Schüler erneut den Umgang mit der Axiomatik, indem sie zeigen,
dass durch die bedingte Wahrscheinlichkeit eine neue Wahrscheinlichkeitsverteilung definiert wird.292 Die Schüler bemerken, dass die Definition der bedingten Wahrscheinlichkeit
ebenso wie die Definition des Begriffs der Wahrscheinlichkeit eine normative Setzung ist,
die die Intuition ausdrücken soll. Mathematisch korrekt ist sie auf jeden Fall, es stellt sich
die eher Frage, ob sie inhaltlich interpretiert sinnvoll ist. Die Axiomatik sollte also erst dann
verwendet werden, wenn die Schüler genügend Erfahrungen gesammelt haben, um diese zu
systematisieren und zu interpretieren. Es wird deutlich, dass die Modellbildung eine subjektive Frage und keine Frage der Wahrscheinlichkeitsrechnung ist.293
290
Büchter; Henn, S. 198.
Tietze; Klika; Wolpers: Didaktik des Mathematikunterrichts, S. 243.
291
Pfeifer: Unabhängige Ereignisse, S. 11.
292
Beweis im Anhang.
Borovcnik: Ein intuitiver Zugang, S. 23.
293
Borovcnik: Zum Anwendungsroblem, S. 216.
74
3.5.2 Arbeitsblatt II - Zufallsvariablen & Erwartungswert/ Varianz
Die Einführung der Zufallsvariablen orientiert sich stark an der beschreibenden Statistik. Die
Schüler sollen erkennen, dass die „Datenreihen als empirische Realisierungen von Zufallsvariablen“ betrachtet werden können.294 Das Merkmal in der beschreibenden Statistik entspricht also der Zufallsvariable in der Wahrscheinlichkeitstheorie. Daraus folgt, dass die
Merkmalsausprägungen den Werten der Zufallsvariablen bzw. die empirische Verteilungsfunktion der Verteilungsfunktion der Zufallsvariablen entsprechen.295
Intuitiv haben die Schüler eine Zufallsvariable beispielsweise bei der Erkundung der Binomialverteilung verwendet, formalisiert wird sie allerdings erst jetzt. Dabei wurde den Schülern eine Definition vorgegeben, die sie auf Beispiele anwenden. Sie erlernen damit den
Umgang mit der mathematischen Sprache. Die drei Zufallsvariablen werden durch das Beispiel des Zufallsexperiments Werfen mit zwei Würfeln verdeutlicht. Die Ergebnismenge
wird sinnvollerweise durch die Menge {(1|1), (1|2),…, (1|6), (2|1), (2|2),…, (5|5), (5|6),
(6|1),…, (6|6)} modelliert. Die Funktion, die jedem Tupel der Ergebnismenge eine reelle
Zahl zuordnet, ist nichts anderes als die Zufallsvariable. Dies wird an den Wahrscheinlichkeitsverteilungen deutlich:
a) Z1: Ω→ ℝ; (a|b)→ a + b
Tabelle 7: Wahrscheinlichkeitsverteilungen für Würfelverteilungen I.
2
3
1
36
4
2
36
5
3
36
6
4
36
7
5
36
8
6
36
9
5
36
4
36
10
3
36
11
2
36
12
1
36
b) Z2: Ω→ ℝ; (a|b)→ max {a, b}
Tabelle 8: Wahrscheinlichkeitsverteilungen für Würfelverteilungen II.
1
2
1
36
3
3
36
4
5
7
36
5
36
6
9
36
11
36
c) Z3: Ω→ℝ; (a|b)→ |a - b|
Tabelle 9: Wahrscheinlichkeitsverteilungen für Würfelverteilungen III.
0
1
6
36
2
10
36
3
8
36
4
6
36
5
4
36
2
36
Tabellen 7-9: Quelle: Lergenmüller: Mathematik Neue Wege, S. 108.
294
Büchter; Henn: S. 282.
Ebd. S. 283.
Eichler; Vogel: Leitfaden. Stochastik, S. 100.
295
75
Den Schülern wird also verständlich, wie sie P(Z=4) berechnen, da dies die Kurzschreibweise für PZ(4) = P(Z-1{4}) = ∑
P(a|b)
(a|b)
Z(a|b)) = 4
darstellt. Die Kurzschreibweise ist sehr
praktisch, da durch sie schnell Wahrscheinlichkeiten von Ereignissen berechnet werden können, wie beispielsweise P(a < Z ≤ b) = ∑c∈Z(Ω) P(Z = c). Allerdings ist sie gewöhnungsbea<c≤b
dürftig, da die Schüler aus der Analysis Aufgabenstellungen der Art ,,gegeben ω, gesucht
Z(ω)“ kennen. Sie bilden also im Graphen senkrechte Schnitte. Im Bereich der Stochastik
ist eher der Aufgabentyp ,,gegeben a, gesucht Z-1(a)“ vorhanden. Es werden also die waagerechten Schnitte gesucht. Dieses Verständnis soll durch das Zeichnen der Balkendiagramme296 der Wahrscheinlichkeitsverteilungen (vgl. Tabellen 7-9) vertieft werden.
Die Wahrscheinlichkeit wird also über die Elementarereignisse berechnet, da es sich um eine
diskrete Zufallsvariable handelt (vgl. Aufgabe 2 des vorhereigen Arbeitsblattes). Die gegebene Definition der Zufallsvariable verallgemeinert dieses Vorgehen:
Ω sei eine diskrete Ergebnismenge. Dann ist eine Zufallsvariable Z eine reellwertige Funktion auf Ω, d.
h. Z: Ω →ℝ; ω→ Z(ω).
Es sei (Ω, P) ein diskreter Wahrscheinlichkeitsraum und Z eine Zufallsvariable auf Ω. Dann wird durch
PZ: P(Z(Ω))→ ℝ, A→ PZ(A) = P(Z-1(A)) eine Wahrscheinlichkeitsverteilung auf der Ereignismenge
P(Z(Ω)) definiert, und (Z(Ω), P Z) ist ein Wahrscheinlichkeitsraum.
Die Funktion einer Zufallsvariable wird vor allem durch den Aufgabenteil 1b) deutlich. Die
Schüler sollen einen Vergleich der Datenanalyse und der Wahrscheinlichkeitsrechnung
durchführen (vgl. Tabelle 10)297:
Tabelle 10: Vergleich Datenanalyse und Wahrscheinlichkeitsrechnung.
Datenanalyse
Merkmal
Merkmalsausprägung
Empirische Häufigkeitsverteilung
Relative Häufigkeit
Arithmetisches Mittel
Standardabweichung in Bezug auf
die Häufigkeitsverteilung
Wahrscheinlichkeitsrechnung
Zufallsvariable
Werte der Zufallsvariablen/ Ereignis
Wahrscheinlichkeitsverteilung der Zufallsvariablen
Wahrscheinlichkeit
Erwartungswert
Standardabweichung in Bezug auf die theoretisch erwartete Streuung der Zufallsvariable
Quelle: Eichler; Vogel: Leitidee Daten und Zufall, S. 241.
296
Besser wäre die Bezeichnung der induzierten Wahrscheinlichkeitsverteilung. Gegebenenfalls kann dieser
Begriff an dieser Stelle geprägt werden. Es wäre auch sinnvoll, die Balken möglichst schmal zu zeichnen, um
zu betonen, dass es sich um einen diskreten Wahrscheinlichkeitsraum handelt.
297
Schupp: Zum Verhältnis, S. 210.
Mittag: Statistik, 159.
76
Durch die Entsprechungen Erwartungswerts/ Arithmetisches Mittel und Standardabweichung (Häufigkeitsverteilung)/ Standardabweichung (theoretische Wahrscheinlichkeitsverteilung) können die Schüler den Erwartungswert und die Varianz bzw. Standardabweichung
analog zur beschreibenden Statistik definieren:298
Es sei (Ω, P) ein diskreter Wahrscheinlichkeitsraum und Z eine Zufallsvariable auf Ω. Dann heißt die
Zahl E(Z)=μZ ∶= ∑x∈Z(Ω) P(Z = x) ∙ x (sofern sie existiert) der Erwartungswert von Z. Die Zahlen
V(Z)∶= ∑x∈Z(Ω) P(Z = x) ∙ (x − E(Z))2 und σZ=√V(Z) heißen (sofern sie existieren) Varianz und Standardabweichung von Z.299
Im Anschluss an die Definition sollte thematisiert werden, dass sowohl der Erwartungswert
als auch die Varianz theoretische Werte sind, die in der Realität nur für große Versuchszahlen gute Schätzungen liefern. Diese Einsicht können die Schüler nur erlangen, wenn die
Probleme der inhaltlichen Wahrscheinlichkeitsbegriffe (stochastischen Konvergenz) thematisiert werden.300
In Aufgabe 2 lernen die Schüler das Spiel „Chuck a Luck“ kennen, an dem die unsichere,
stochastische Konvergenz für Mittelwerte thematisiert wird. In dem Spiel setzt ein Spieler
seinen Einsatz (z.B. ein Euro) auf eine Augenzahl seiner Wahl (=x). Anschließend wirft der
Bankhalter mit drei Würfeln. Je nachdem wie viele Würfel die gesetzte Augenzahl zeigen,
bekommt der Spieler den Einsatz einfach, doppelt, oder dreifach zurück. Ansonsten hat er
den Einsatz verloren. Die Idee des fairen Spiels soll inhaltlich mit dem Erwartungswert verknüpft werden. Die Schüler diskutieren daher zunächst, wie ein faires Spiel mathematisch
dargestellt werden kann. Die meisten werden hier für einen Erwartungswert gleich 0 plädieren. Allerdings kann auch ein positiver Erwartungswert als fair angesetzt werden. Letztendlich wird ersichtlich, dass ein faires Spiel eine normative Setzung darstellt.301
Anschließend führen die Schüler das Spiel Chuck a Luck ein paar Mal durch und notieren
ihren durchschnittlichen Nettogewinn. Dies soll das empirische Gesetz der großen Zahlen
für Mittelwerte vorbereiten, das in Aufgabenteil d) entdeckt wird.302 Vorher stellen die Schüler jedoch die Zufallsvariable Z und die Wahrscheinlichkeitsverteilung (vgl. Tabelle 11) auf:
3, falls a = b = c = x.
2, falls zwei x − er dabei sind.
Z: Ω→ ℝ; (a|b|c)→ {
1, falls ein x dabei ist.
−1, falls kein x dabei ist.
298
Engel: Wahrscheinlichkeitstheorie und Statistik, S. 76.
Büchter; Henn: Elementare Stochastik, S. 285.
300
Bieler: Gesetze, S. 18.
301
Büchter; Henn: Elementare Stochastik, S. 285.
302
Dieses hätte auch im Kapitel „Der frequentistische Wahrscheinlichkeitsbegriff“ behandelt werden können.
Die Arbeit konzentriert sich allerdings auf die Stärken und Schwächen der Wahrscheinlichkeitsbegriffe. Wahrscheinlichkeitsverteilungen werden sozusagen als Hilfsmittel bzw. als Exkurs angesehen.
299
77
Tabelle 11: Chuck a Luck.
Y
P(Z=y)
-1
125
216
1
75
216
2
15
216
3
1
216
Quelle: Büchter; Henn: Elementare Stochastik, S. 282.
Mit diesen Werten können nun Erwartungswert und Varianz bzw. Standardabweichung bestimmt werden:
125
75
15
1
17
μ=E(Z)=216 ∙ (−1) + 216 ∙ 1 + 216 ∙ 2 + 216 ∙ 3=− 216 ≈ -0,07.
125
75
15
1
57815
V(Z)=216 ∙ (−1 − μ)² + 216 ∙ (1 − μ)² + 216 ∙ (2 − μ)² + 216 ∙ (3 − μ)²=46656 ≈ 1,24 und
somit σZ ≈ 1,11.
Die Spielenden des Chuck a Luck verlieren also auf lange Sicht sieben Cent pro Runde.
Ähnlich wie bei der relativen Häufigkeit kann für ein einzelnes Spiel nur die bestmögliche
Wahl getroffen werden. Erst auf lange Sicht stabilisiert sich das arithmetische Mittel um den
Erwartungswert.303 Da die Standardabweichung zusätzlich im Betrag größer als der Erwartungswert ist, muss die Bank das Spiel lange spielen, um die sieben Cent pro Spiel zu gewinnen. Bei kleinen Versuchszahlen kann ähnlich wie bei der relativen Häufigkeit alles passieren. Diese Tatsache soll durch die Simulation des Chuck a Luck Spiel deutlich werden.
Insbesondere wird erneut die unsichere Stabilisation der Werte vermittelt (vgl. Abbildung
16).304
Abbildung 16: Chuck a Luck.
Lergenmüller: Mathematik Neue Wege, S. 112.
Diese Schwankungen werden im Zugang über die Axiomatik mit einer Zufallsvariable einer
Wahrscheinlichkeitsverteilung verdeckt.305 Dieses deterministische Vorgehen verhindert
ohne die Reflexion der Ergebnisse das stochastische Denken.306
303
Barth; Haller: Soll ich, S. 20.
Schupp: Das Galtonbrett, S. 15.
305
Engel: Entdecken von Wahrscheinlichkeitsverteilungen, S. 6.
306
Heymann: Allgemeinbildender Mathematikunterricht, S. 8.
304
78
In der dritten Aufgabe erlernen die Schüler Rechenregeln für den Erwartungswert sowie für
die Varianz einer Zufallsvariable, die anschließend auf die Binomialverteilung angewendet
werden. Die Schüler experimentieren mit einer Excel-Tabelle, um Antworten auf folgende
Fragen zu erhalten: Wie verändert sich der Erwartungswert E(Z) einer Zufallsvariable Z,
wenn man zu Z eine Konstante c addiert? Was passiert mit dem Erwartungswert E(Z), wenn
die Zufallsvariable Z mit einem konstanten Faktor multipliziert wird? Wie hängt der Erwartungswert von Y + Z von den Erwartungswerten Y und Z ab? Schließlich erhalten sie die
Rechenregeln E(Z+10)=E(Z) + 10, E(a∙Z) = a ∙ E(Z) und E(Y+Z) = E(Y) + V(Z). Die analogen Rechenregeln für die Varianz wurden den Schülern vorgegeben. Diese sollten sie lediglich an Beispielen verifizieren. Sie lauten: V(a∙Z +c)=a ∙ V(Z) und falls Y und Z unabhängig sind: V(Y+Z)=V(Y) + V(Z). Für die Formeln des Erwartungswertes sollen die Schüler ein Beispiel aus der Glücksspielwelt erfinden. Diese Vorgehensweise wird Prinzip der
Reversibilität genannt. So kann beispielsweise für die Rechenregel E(X+a) = E(X) + a eine
Lotterie betrachtet werden, bei der die Gewinne in jeder Gewinnklasse um a € erhöht werden.307
Diese Erkenntnisse sollen auf die Binomialverteilung übertragen werden. Die Bestimmung
des Erwartungswertes ist durch dessen Definition nur schwer möglich, denn dazu müsste die
Gleichung E(Z)= ∑ni=1(nk) ∙ pk ∙ (1-p)n-k ∙ k vereinfacht werden. Einfacher ist die Rechenregeln zu beachten und die Zufallsvariable Z als zusammengesetzte Bernoulli-Experimente
aufzufassen und als Z = ∑ni=1 Zi zu schreiben. Zi soll dabei den i-ten Teil des Zufallsexperimentes darstellen. Da Zi(Treffer) = 1 und Zi(Niete) = 0 ist, gilt P(Zi=1) = p und P(Zi=0) = 1p, woraus der Erwartungswert E(Zi) = p folgt. Durch die Rechenregel E(Y+Z) = E(Y) + E(Z)
kann E(Z) = E(∑ni=1 Zi) = n∙p gefolgert werden. Die Varianz kann analog als V(Z) = n∙p∙(1p) berechnet werden. Dafür mussten die Zi unabhängig sein, was durch die Binomialverteilung gegeben ist.308
In der Vertiefung soll nochmal auf die Definition des Erwartungswertes eingegangen und
erneut auf die Problematik von unendlichen Ergebnismengen hingewiesen werden. Dazu
eignet sich das St. Petersburger Paradoxon. Das Problem geht auf Cardano zurück und hat
die Entwicklung der Stochastik stark beeinflusst. Zwei Spielende werfen eine Münze bis
zum ersten Mal Kopf fällt. Geschieht dies beim ersten Mal, so erhält ein Spieler A vom
Spieler B 2€. Kommt Kopf erst beim zweiten Mal, erhält er 4€, beim dritten Mal 8€ usw.
Kommt Kopf also erst beim n-ten Wurf, so erhält der Spieler B 2n €. Es stellt sich die Frage,
307
308
Lergenmüller: Mathematik Neue Wege, S. 116.
Büchter; Henn: Elementare Stochastik, S. 308.
79
was Spieler B einsetzen soll, damit das Spiel fair ist. Durch die Formulierung des fairen
1
1
Spiels berechnen die Schüler zunächst den Erwartungswert und erhalten E(Z) = 2 ∙ 2 + 4 ∙
1
4+. . . + (2)n ∙ 2n + … = 1+1+…+1+…= ∞. Spieler B müsste also ∞ € einsetzen, das bedeutet
das jeder Einsatz für Spieler B zu gering wäre. Dieses Paradoxon löst sich auf, wenn man
sich die Definition des Erwartungswertes anschaut, da dieser in diesem Fall nicht existiert.309
Der zweite Teil der Aufgabe besteht aus der Berechnung des Erwartungswertes und der
Standardabweichung einer Binomialverteilung, die geübt werden sollen. Hierbei wurden die
Werte der Binomialverteilung der Aufgabe 1 des Arbeitsblattes „Der frequentistische Wahrscheinlichkeitsbegriff I“ wieder aufgegriffen. An dieser Stelle bekommen die dort eingeführten Bezeichnungen „linkssteil“, „rechtssteil“ oder „symmetrisch“ eine mathematische
Bedeutung. Außerdem wird die Auswirkung der Versuchsanzahl auf die Binomialverteilung
in Aufgabe 2 des nächsten Arbeitsblattes (Der axiomatische Wahrscheinlichkeitsbegriff III)
vertieft. Die Schüler können so die numerischen Werte mit einem Graphen verknüpfen.
Im letzten Teil der Vertiefung werden Behauptungen im Format „Richtig oder Falsch“ aufgestellt, die die Thematik vertiefen und den Beweis des schwachen Gesetzes der großen
Zahlen auf dem nächsten Arbeitsblatt vorbereiten. So ist der Erwartungswert proportional
zur Versuchszahl n, was sich aus μ = n∙p ableitet. Dagegen ist die Standardabweichung proportional zu √n. Diese Tatsache soll die Schüler an das
1
-Gesetz erinnern, das ebenfalls auf
√n
dem nächsten Arbeitsblatt vertieft wird. Außerdem erlernen die Schüler, dass die Stan1
dardabweichung bei fester Versuchszahl am größten ist, wenn p = 2. Dies kann leicht herge1
leitet werden, denn der quadratische Term p∙(1-p) hat sein Maximum bei p = 2.310
3.5.3 Arbeitsblatt III - Das schwache Gesetz der großen Zahlen
Die Schüler haben bisher gelernt, dass das empirische Gesetz der großen Zahlen einen
Grenzwert im analytischen Sinne nicht garantiert. Es dient „nur“ dazu (theoretisch) wiederholbaren Ereignissen, Wahrscheinlichkeiten zuzuschreiben. Diese Schätzung ist stets subjektiv, da verschiedene Versuchsreihen auch andere Schätzungen hervorbringen. Der frequentistische Wahrscheinlichkeitsbegriff geht davon aus, dass jedes Ereignis eine innewohnende bzw. objektive Wahrscheinlichkeit besitzt. Dahinter steht die Vorstellung, dass die
relativen Häufigkeiten stochastisch konvergieren. Das Bernoulli‘sche Gesetz der großen
309
Götz; Humenberger: Das Problem, S. 50.
Krämer: Denkste, S. 128.
Székely: Paradoxa, S. 35.
310
Lergenmüller: Mathematik Neue Wege, S. 132.
80
Zahlen trifft mit Hilfe des axiomatischen Wahrscheinlichkeitsbegriffs eine mathematische
Aussage darüber, wie wahrscheinlich das Verbleiben der relativen Häufigkeiten im ɛSchlauch ist. Die Schüler ordnen in Aufgabe 1 den Beweis für das schwache Gesetz der
großen Zahlen. Dabei wurden ebenfalls Erläuterungen der einzelnen Formeln formuliert, um
das Verständnis der Schüler für das schwache Gesetz der großen Zahlen zu erhöhen. Abschließend halten die Schüler in verkürzter Form folgenden Beweis fest:311
Voraussetzung für das Bernoulli‘sche Gesetz der großen Zahlen ist die Ungleichung von
Tschebycheff312 für Zufallsvariablen:
Sei (Ω,P) ein diskreter Wahrscheinlichkeitsraum und Z eine Zufallsvariable auf Ω mit dem Erwartungswert μ und der Standardabweichung σ. Dann gilt: P(|Z-μ| ≤ ɛ) > 1-
σ²
ɛ²
.
Die Ungleichung von Tschebycheff gibt an, mit welcher Wahrscheinlichkeit die Werte einer
Zufallsvariable in ein vorgegebenes Intervall um den Erwartungswert fallen. Diese Abschätzung ist relativ schlecht313, aber dennoch für alle Zufallsvariablen gültig. Bernoulli benutzte
diese Ungleichung, um die Annäherung der relativen Häufigkeit an die unbekannte Wahrscheinlichkeit mathematisch darzustellen. Durch die Allgemeingültigkeit der TschebycheffUngleichung konnte sich Bernoulli auf eine B(n,p)-verteilte Zufallsvariable Z beschränken.314 Dabei sind ihm der Erwartungswert E(Z) = n·p und die Varianz V(Z) = n·p·(1-p)
1
bereits bekannt. Bernoulli definierte sich eine neue Zufallsvariable Z‘∶= n·Z, um die relative
Häufigkeit beschreiben zu können. Durch die Eigenschaften des Erwartungswert und der
Varianz erhält er auch für diese Zufallsvariable die entsprechenden Kenndaten: E(Z‘) = p315
und V(Z‘) =
p · (1−p)
n
.
Diese Kenndaten ersetzt Bernoulli in der Ungleichung von Tschebycheff, sodass er P(|Z-p|
≤ ɛ) > 1 -
p · (1−p)
n · ɛ²
erhält. Den größten Wert, den der Zähler p · (1 - p) annehmen kann, liegt
1
bei 4. Hieraus folgt das Bernoulli‘sche Gesetz der großen Zahlen:
311
Die Fußnoten erläutern einige Tatsachen im mathematischen Sinn. Diese sind für die Schüler an dieser
Stelle nicht relevant.
312
Eine analoge Ungleichung gibt es auch für die beschreibende Statistik. Dort liefert sie eine Abschätzung für
die relative Häufigkeit der Werte, die in ein vorgegebenes Intervall um das arithmetische Mittel fallen. Die
Entsprechungen von Merkmal und Zufallsvariable liefern direkt die Tschebycheff-Ungleichung für Zufallsvariablen.
313
Sie könnte durch weitere Voraussetzungen, z.B. eine vorausgesetzte Normalverteilung verbessert werden.
314
Eichler; Vogel: Leitfaden Stochastik, S. 165.
315
Der Erwartungswert der Zufallsvariablen ist unabhängig von n, das heißt der Erwartungswert der relativen
Häufigkeit ist p. Die relative Häufigkeit ist also ein erwartungstreuer Schätzer.
81
Sei (Ω, P) ein endlicher Wahrscheinlichkeitsraum und E⊆Ω ein Ereignis mit der Wahrscheinlichkeit
P(E) = p. Die Zufallsvariable Z´ beschreibe die relative Häufigkeit des Eintretens von E bei n unabhän1
gigen Versuchen. Dann gilt: P(|Z´- p| ≤ ɛ) > 1und
lim P(|Z′ − p| ≤ ɛ316) = 1.317
4 · n · ɛ²
n→∞
Die erste Aussage ist in der Praxis sehr hilfreich, da ein Zufallsexperiment nur endlich oft
wiederholt werden kann. Das bedeutet, dass es sich um endliche Wahrscheinlichkeitsräume
handelt. Die erste Ungleichung gibt also eine Antwort auf die Frage, wie oft gewürfelt werden muss, um beispielsweise die Wahrscheinlichkeit auf ɛ = 1% genau mit einer Sicherheit
1
von 99% zu schätzen. Nach dem Gesetz der großen Zahlen müsste tatsächlich 1- 4 · n · ɛ² ≥
0,99, das heißt mindestens 250.000-mal gewürfelt werden. Dies ist praktisch nicht zu realisieren und zeigt die Schwäche des frequentistischen Ansatzes.
Die zweite Aussage umfasst eine Grenzwertaussage im Sinne der Analysis. Durch sie konnte
die Lücke zwischen Empirie und Theorie geschlossen werden. Bisher konnte durch das empirische Gesetz der großen Zahlen lediglich eine Stabilisierung der relativen Häufigkeiten
gesichert werden. Nun kann sogar eine Stabilisierung in der Nähe der von p (Erwartungswert
von Z‘) vermutet werden.318 Wahrscheinlichkeiten können also (unter diesen Bedingungen)
wie physikalischen Größen gemessen werden, da die relative Häufigkeit als gute Schätzgröße für die Wahrscheinlichkeit angesehen werden kann.319
Weiterhin erstellen die Schüler in Aufgabenteil 1c) eine Tabelle, in der sie das empirische
Gesetz der großen Zahlen mit dem schwachen Gesetz der großen Zahlen vergleichen (vgl.
Tabelle 12). Dabei wird vor allem der Unterschied zwischen der analytischen und der
stochastischen Konvergenz sichtbar:
Tabelle 12: Vergleich empirisches und schwaches Gesetz der großen Zahlen.
Empirisches Gesetz der großen Zahlen
- Stabilisierung der relativen Häufigkeiten.
- Setzt große Versuchsreihen voraus.
- Kann ohne den Begriff der Wahrscheinlichkeit formuliert werden.
- Relative Häufigkeiten gehen im Unendlichen zu Wahrscheinlichkeiten über.
- Unklar: n groß genug, stabilisiert sich.
- Ab einem gewissen n müsste die relative
Häufigkeit in der ɛ-Umgebung bleiben
(Idee von von Mises).
Schwaches Gesetz der großen Zahlen
- Theorie des Wahrscheinlichkeitsraums
von Kolmogorov (axiomatischer Wahrscheinlichkeitsbegriff).
- Grenzwertaussage im Sinne der Analysis.
- Gibt ein n an, so dass die relative Häufigkeit ab diesem n mit einer gewissen Wahrscheinlichkeit (z.B. 95%) in der ɛ-Umgebung verbleibt.
Quelle: Eigene Konzeption.
An dieser Stelle könnte man versucht sein ε=0 zu setzen. Bereits Bernoulli hat darauf hingewiesen, dass
dann lim 𝑃(|𝑍´ − 𝑝| = 0)=0. Vgl. Barth: Leistungskurs, S. 249.
316
317
𝑛→∞
Bosch: Elementare Einführung, S. 52.
318
Eichler; Vogel: Leitfaden Stochastik, S. 164.
319
Tietze; Klika; Wolpers: Mathematik in der Sekundarstufe II, S. 28.
82
Für das starke Gesetz der großen Zahlen müsste eine unendliche Folge von Zufallsexperimenten betrachtet werden. Diese ist selbst für ein endliches Omega mit zwei Elementen nicht
mehr abzählbar, sodass für einen Beweis der axiomatische Aufbau mit überabzählbaren
Mengen notwendig ist.320 Das starke Gesetz der großen Zahlen zeigt, warum der Definitionsversuch von Mises scheiterte. Die Konvergenz einer Folge der relativen Häufigkeiten ist
nur „fast sicher“, was bedeutet, dass „verrückte“ Folgen können nicht ausgeschlossen, sondern nur mit der Wahrscheinlichkeit 0 versehen werden können. Allerdings ist es für die
Schule sinnvoller, sich auf die Schwankungen der relativen Häufigkeiten zu konzentrieren
und nicht auf die fast sichere Konvergenz, die den Eindruck der Unsicherheit verdecken
würde. Daher wird das starke Gesetz der großen Zahlen didaktisch reduziert.321
Beim schwachen Gesetz der großen Zahlen wird die Stärke der Axiomatik sehr deutlich.
Ähnlich wie beim Laplace-Ansatz könnte ein Zirkelschluss in der Definition vermutet werden, da der Zusammenhang zwischen der relativen Häufigkeit und der Wahrscheinlichkeit
schon zur Definition bzw. Interpretation der Wahrscheinlichkeit verwendet wurde. Jedoch
liegt dieser Zirkelschluss nicht vor, da die Wahrscheinlichkeit im Axiomensystem völlig
unabhängig von inhaltlichen Betrachtungen und somit auch von der relativen Häufigkeit definiert wurde. Zudem wird deutlich, dass das empirische Gesetz der großen Zahlen die Stabilisierung nicht exakt fassen konnte, weil der Begriff der Wahrscheinlichkeit fehlt.322
Analog zum Arbeitsblatt „Das empirische Gesetz der großen Zahlen“ kann die Frage gestellt
werden, wie gut einem gefundenen Schätzwert vertraut werden kann. Dafür berechnen die
Schüler in Aufgabe 2 zunächst die Wahrscheinlichkeit, dass die Trefferanzahl von Zahl (Z)
vom Erwartungswert μ um nicht mehr als die Standardabweichung σ in Abhängigkeit von n
abweicht. Dies kann mathematisch als P(|Z-μ| ≤ σ) ausgedrückt werden. Die Werte für n =
50, n = 100 und n = 500 betragen 0,624; 0,6763 und 0,6581. Die Schüler vermuten daher,
dass die berechneten Wahrscheinlichkeiten fast unabhängig vom Versuchsumfang n sind
und sich bei hinreichend großen n kaum noch ändern.323 Damit haben die Schüler die sogenannten Sigma-Regeln entdeckt. Zusammen mit Aufgabe b) können diese σ-Umgebungen
von μ festgehalten werden: P(|Z-μ| ≤ σ) ≈ 68,3%, P(|Z-μ| ≤ 2σ) ≈ 95,5%, P(|Z-μ| ≤ 3σ) ≈
99,7%.324
320
Barth: Leistungskurs, S. 250.
Fischer; Lehner; Puchert: Einführung in die Stochastik, S. 246.
322
Barth: Leistungskurs, S. 251.
323
Eine Faustregel besagt, dass die Sigma-Regeln gute Werte liefern, falls σ>3. Vgl. Lergenmüller: Mathematik Neue Wege, S. 129.
324
Ebd. S. 129.
321
83
Als Info-Text bekommen die Schüler den umgekehrten Weg geliefert, das heißt in welches
zum Erwartungswert symmetrische Intervall die Trefferwahrscheinlichkeit X mit einer bestimmten Wahrscheinlichkeit fällt. Zum Beispiel nimmt man für eine 95%ige-Sicherheit an,
dass P(|X-μ| ≤ a) ist (a = 1,96 ∙ σ). Daher wird das Intervall [μ - 1,96∙σ; μ + 1,96 ∙ σ] als das
95%-Prognoseintervall bezeichnet.325
Die Bezeichnung 95%-Prognoseintervall kennen die Schüler bereits in Verbindung mit dem
1
-Gesetz. Ein Ziel dieser Aufgabe ist die Formalisierung dieses empirischen „Naturgeset-
√n
zes“ mit Hilfe der Axiomatik.326 Darüber hinaus bildet die Aufgabe die Möglichkeit, die
Stabilisierung der relativen Häufigkeit erneut zu begründen sowie die Stabilisierung der absoluten Häufigkeit zu widerlegen. Dies wird den Schülern ersichtlich, da die 95%-Prognoseintervalle für die absolute Häufigkeit mit wachsender Versuchszahl immer größer werden
und für die relative Häufigkeit immer kleiner. Schließlich können die Schüler für den Spezialfall begründen, dass das 95%-Prognoseintervall mit wachsendem n proportional zu
1
√n
kleiner wird. Dafür müssen sie lediglich die Breite des Prognoseintervalls bestimmen (2∙
σ
1
1,96 ∙ n) und σ durch die Formel √n ∙ p ∙ (1 − p) ersetzen (p = 2).327
Als letzte Aufgabe werden die Wahrscheinlichkeitsbegriffe in einer Fishbowl-Diskussion328
abgeschlossen. Dabei ziehen die Schüler jeweils eine Karte, auf der eine historische Figur
abgebildet ist, die die verschiedenen Wahrscheinlichkeitsbegriffe repräsentiert. Laplace
steht für den Laplace-, von Mises für den frequentistischen, Bayes für den subjektiven und
Kolmogorov für den axiomatischen Wahrscheinlichkeitsbegriff. Damit soll zum einen
Fremdverstehen gefördert werden und zum anderen klar werden, dass nicht die Schüler
selbst das Modell präferieren, sondern die historische Person. Dies soll den Einstieg in die
Diskussion erleichtern. Die Schüler bereiten sich in ihrer Gruppe auf die Diskussion vor, in
dem sie die Stärken und Schwächen der verschiedenen Modelle reflektieren. Dabei sollen
sie auch Strategien entwickeln, um auf Argumente zu reagieren und ihren eigenen Standpunkt zu vertreten.329
325
Das Prognoseintervall kann auch also Ellipse bzw. als Kreis dargestellt werden. Dies kann den visuellen
Lerntyp ansprechen. Vgl. Ineichen: Wie könnte man, S. 93.
326
Schnell: Muster und Variailität, S. 23.
327
Lergenmüller: Mathematik Neue Wege, S. 132.
Vanscó; Warmuth: Schwierigkeiten, S. 34.
328
Die Methode Fishbowl hat den Vorteil, dass aus jeder Gruppe zunächst nur eine Person diskutiert, die jedoch
von einer anderen Person aus der Gruppe unterstützt werden kann.
329
Mögliche Argumente erschließen sich aus Tabelle im Anhang.
84
4. Die stochastische Modellbildung
Durch den alternativen Zugang zur Stochastik wurde deutlich, dass stochastische Fragestellungen erst nach dem Aufstellen eines mathematischen Modells gelöst werden können. Daher wurde ein weiteres Aufgabenblatt erstellt, das den Modellierungskreislauf vertieft behandelt. Es kann am Ende des Themengebietes „Stochastik“ behandelt werden.
Im Kapitel „Der axiomatische Wahrscheinlichkeitsbegriff“ haben die Schüler gelernt, dass
die Axiomatik Kolmogorovs den Wahrscheinlichkeitsbegriff präzise festlegt. Dazu war eine
Abkehr von der konkreten Situation notwendig. Dennoch soll die Wahrscheinlichkeitslehre
letztendlich Probleme aus der Realität lösen. Der folgende Modellkreislauf (vgl. Abbildung
17) stellt eine Möglichkeit dar, mit diesem scheinbaren Widerspruch umzugehen.330
Abbildung 17: Stochastische Modellbildung.
Quelle: Büchter; Henn: Elementare Stochastik, S. 199.
Die Schüler beschreiben in Aufgabe 1 den Modellkreislauf und übertragen diesen auf die
Aufgabe „Der Riemerquader“ des Arbeitsblatts „Der Einstieg in die Stochastik“: Im Modellkreislauf wird von einer realen Situation ausgegangen, in der Ergebnisse festgelegt werden, sodass ein Realmodell entsteht. Dann wird eine Wahrscheinlichkeitsverteilung P: Ϝ→
ℝ festgelegt, welche die Kolmogorov-Axiome erfüllt. Somit ist ein mathematisches Modell
konstruiert. Mit Hilfe der Wahrscheinlichkeitstheorie können weitere Wahrscheinlichkeiten
berechnet werden. Man erhält also mathematische Resultate, die in der Realität gedeutet
werden müssen. Mathematisch gesehen ist das Modell weder falsch noch richtig, das heißt
je nach Modell erfolgen korrekte mathematische Folgerungen.331
Deutlich wird dieser Modellkreislauf im Einstiegsproblem des Riemer-Quaders. Im LaplaceAnsatz werden die Funktionswerte von der Wahrscheinlichkeitsfunktion so gedeutet, dass
alle Elementarergebnisse den gleichen Wert haben. Der frequentistische Ansatz benutzt die
330
Büchter; Henn: Elementare Stochastik, S. 199.
Ebd. S. 200.
Schupp: Zum Verhältnis, S. 209.
Sill: Zur Modellierung, S. 13.
331
85
bekannten relativen Häufigkeiten als Werte von P. Im subjektiven Ansatz werden die Funktionswerte allein auf Grund subjektiver Einschätzungen getroffen. Beim Riemer-Quader ist
beispielsweise das Modell der Gleichwahrscheinlichkeit in der Realität nicht sinnvoll. Dennoch ist an den mathematischen Folgerungen nichts zu kritisieren. Am Riemer-Quader wird
auch deutlich, dass die verschiedenen Modelle sich nicht gegenseitig ausschließen. Ausgehend von den relativen Häufigkeiten könnten die gleich großen Flächen trotz kleiner Unterschiede in den relativen Häufigkeiten mit der gleichen Wahrscheinlichkeit versehen werden.
Hier ist eine Kombination des frequentistischen und des Laplace-Modells klar zu erkennen.
Es wird deutlich, dass die Modellbildung eine subjektive und keine Frage der Wahrscheinlichkeitsrechnung ist. Es ist daher elementar wichtig, die Chancen und Risiken der Wahrscheinlichkeitsbegriffe zu kennen, um ein angemessenes Modell aufzustellen. Für die Lehrkräfte bedeutet das, dass die „vermeintliche Sicherheit des Expertenwissens ein Stück weit
zugunsten echter Anwendung aufzugeben“332 ist.
Die hohe Bedeutung des Modellierungsaspekts stellt das sogenannte Sehnenparadoxon von
Bertrand (Aufgabe 2) dar, in dem ein Kreis mit dem Radius r gegeben ist. Die Schüler sollen
die Frage beantworten, wie groß die Wahrscheinlichkeit ist, dass eine zufällig in diesen Kreis
gezogene Sehne länger als die Seite des einbeschriebenen gleichseitigen Dreiecks ist. Bereits
Bertrand thematisierte in seinem Werk „Calcules des probabilités“ drei Wege,333 wie das
Problem gelöst werden kann. Dies liegt daran, dass in der Aufgabe offen gelassen wird, wie
die Auswahl der Sehnen erfolgen soll. Die folgenden Modellierungen sind also nicht Lösungen einer Aufgabe, sondern Lösungen von verschiedenen Aufgaben.334
In der ersten Modellierungsidee wird ein Punkt im Inneren des Kreises gewählt, der Mittelpunkt der Sehne ist (vgl. Abbildung 18). Die Sehne ist somit fest gewählt. Falls die Sehne
länger als die Seitenlänge a sein soll, muss der Mittelpunkt in einem Kreis mit Radius
liegen. Daraus folgt P =
r2
∙π
4
2
r ∙π
r
2
1
= 4.335
332
Ullmann: Diagramme, S. 59.
Es können weitere Modellierungen gefunden werden. Vgl. Büchter; Henn: Elementare Stochastik, S. 253.
334
Kütting; Sauer; Padberg: Elementare Stochastik, S. 123.
Borovcnik: A Probabilistic Perspektiv, S. 60.
335
Kütting; Sauer; Padberg: Elementare Stochastik, S. 123.
Székely: Paradoxa, S. 51
333
86
Abbildung 18: Lösung Sehnenproblem I.
Quelle: Kütting; Sauer; Padberg: Elementare Stochastik, S. 123.
Die zweite Modellierung geht davon aus, dass ein Punkt auf dem Kreis gewählt wird, der
der Eckpunkt eines gleichseitigen Dreiecks ist (vgl. Abbildung 19). Damit die Sehne größer
als die Seitenlänge ist, muss der zweite Endpunkt der Sehne auf dem Kreisbogen BC liegen.
1
Da die drei möglichen Kreisbögen gleich lang sind, folgt P = 3.336
Abbildung 19: Lösung Sehnenproblem II.
Quelle: Kütting; Sauer; Padberg: Elementare Stochastik, S. 123.
Außerdem kann ein Punkt auf einem festen Durchmesser des Kreises gewählt werden (vgl.
Abbildung 20). Der Höhenfußpunkt H halbiert die Strecke AM. Daher stammen alle Sehnen,
die kürzer als die Dreiecksseite sind, vom obersten und vom untersten Viertel des Durch1
messers, sodass sich eine Wahrscheinlichkeit von P = 2 ergibt.337
Abbildung 20: Lösung Sehnenproblem III.
Quelle: Kütting; Sauer; Padberg: Elementare Stochastik, S. 123.
336
Kütting; Sauer; Padberg: Elementare Stochastik, S. 123.
Székely: Paradoxa, S. 51.
337
Büchter; Henn: Elementare Stochastik, S. 256.
87
Alle drei Modellierungen sind mathematisch korrekt. Die unterschiedlichen Ergebnisse
kommen durch die Interpretation des Wortes „zufällig“ zustande.338 Den Konflikt auszuhalten, dass es mehr als eine richtige Lösung gibt, ist ein entscheidendes Ziel der Allgemeinbildung im Mathematikunterricht.339
Abschließend wird eine Abituraufgabe (Hessen, Grundkurs 2010) analysiert, in der die Probleme deutlich werden, die durch die Umsetzung des in der Einleitung beschriebenen Vorgehens des Lehrplans entstehen.340 In der Aufgabe stellt eine Schokoladenfirma Überraschungseier her, in denen jedes fünfte Ei eine Simpsons-Figur enthalten soll. Die Überraschungseier können im Geschäft einzeln oder in einer Schachtel gekauft werden. Bis zu diesem Punkt stellt die Aufgabe einen anwendungsbezogenen Kontext her, der Ähnlichkeiten
zu der Aufgabe „Warum gibt es immer so wenige rote Gummibärchen in der Tüte?“ aufzeigt.
Der letzte Satz des einleitenden Textes irritiert jedoch stark: „Es wird garantiert, dass auch
in jeder Schachtel die Anzahl der Eier mit einer Simpsons-Figur dem angegebenen Anteil
entspricht.“341 Anstatt im sinnvollen frequentistischen Modell zu bleiben oder eine LaplaceHypothese aufzustellen, wird der Anteil
1
5
für eine Schachtel „garantiert“. Damit geht das
Wesen der Stochastik verloren. Wenn sich in jeder Schachtel genau
1
5
Simpsons-Figuren
befinden, müssen keine wahrscheinlichkeitstheoretischen Fragen mehr gestellt werden. Die
Aufgabensteller wollten den Schülern die Modellierung der Aufgabe mit Hilfe des frequentistischen Modells abnehmen und zerstörten dadurch die Situation. Besonders deutlich wird
dies an Teilaufgabe 3.2. Nachdem 100 Überraschungseier, die für ein Schulfest gekauft wurden, geöffnet wurden und nur 16 Figuren enthalten waren, beschwerten sich die Schüler bei
der Überraschungseierfabrik. Diese antworteten ihnen, dass dies in einem Bereich liegt, der
nicht unwahrscheinlich ist. Im frequentistischen Modell, in dem Schwankungen der relativen
Häufigkeiten normal sind, ergibt die Aufgabe einen Sinn. Mit Einbezug des garantierten
Anteils an Simpsons-Figuren kann es jedoch keine Zufallsschwankungen geben. Im einleitenden Text der Aufgabe hätte daher den Schülern die Modellierung überlassen werden sollen. Bei einer stärkeren Lenkung könnte auch der Anteil von
1
5
als Hypothese vorgegeben
werden („Die Schokoladenfabrik behauptet, dass jedes fünfte Ei eine Figur enthält“).342
338
Büchter; Henn: Was heißt, S. 122.
Schmidt: Schwächen, S. 24.
340
Abituraufgaben Hessen.
341
Ebd.
342
Dabei wird dafür plädiert, dass die Schüler den Modellierungscharakter auch in Abituraufgaben selbst übernehmen sollen. Einige Didaktiker sehen dies allerdings nicht als Teil einer Abiturprüfung an.
339
88
Auch in Aufgabe 2 der Abiturprüfung zeigt sich diese Modellierungsproblematik. Wieso
sollte ein Schüler die Wahrscheinlichkeit bestimmen, dass genau vier Figuren in einer
1
Schachtel sind? Dieser Aspekt ist bereits bekannt, da der Anteil von 5 in jeder Schachtel (20
Eier) garantiert wird. Lässt man diese Modellierungsproblematik außer Acht und betrachtet
die Musterlösungen wird ein weiteres Problem deutlich, das mit den Wahrscheinlichkeitsbegriffen eng verbunden ist. Die Schüler können sowohl die Binomial- als auch die Normalverteilung verwenden, um die Wahrscheinlichkeit für genau vier Figuren in einer Schachtel
zu bestimmen. Allerdings ist in diesem Kontext das kontinuierliche Modell der Normalverteilung unbegründet, da lediglich mit Hilfe einer diskreten Wahrscheinlichkeitsverteilung,
hier die Binomialverteilung, dieses Problem angemessen modelliert werden kann. Die Schüler haben gelernt, dass einer einelementigen Menge in einem kontinuierlichen Wahrscheinlichkeitsmodell die Wahrscheinlichkeit 0 zugeordnet werden muss. In Aufgabe 2.1 wird dieses Verständnis umgesetzt und in der Musterlösung nur die Binomialverteilung angegeben.
Dagegen wird in Aufgabe 3 eine Annäherung, dass in 100 Packungen 20 Figuren vorhanden
sind, mit der Normalverteilung angegeben.
Auch beim Berechnen der Wahrscheinlichkeit in Aufgabe 2.2, in der die Wahrscheinlichkeit
für mehr als vier Figuren in einer Schachtel bestimmt werden soll, ist die Normalverteilung
kein brauchbares Modell. Die Wahrscheinlichkeit für die einzelnen Summanden würde im
kontinuierlichen Modell 0 betragen, sodass auch die Wahrscheinlichkeit insgesamt 0 betragen würde. Nur mit Hilfe der Binomialverteilung kann die realitätsnahe Wahrscheinlichkeit
von 37% ermittelt werden. Darüber hinaus wurde auch die Faustregel vernachlässigt, dass
die Binomialverteilung durch die Normalverteilung angenähert werden kann, wenn σ>3 beträgt. So wird auch das Ergebnis 50% bei der Anwendung der Normalverteilung als richtiges
Ergebnis akzeptiert. Der 23%ige Unterschied in den Werten wird weder erwähnt noch reflektiert.
Insgesamt zeigt sich, dass in der Abituraufgabe die Modelle unreflektiert an eine Aufgabe
herangetragen werden. Es wird ein kontinuierliches Modell verwendet, obwohl die Aufgabe
durch ein diskretes Modell besser beschrieben werden würde. Außerdem werden Voraussetzungen, wie die σ>3-Regel nicht beachtet. Die Schwierigkeiten des Lehrplans werden durch
das „Garantieren“ eines Anteils an Figuren am deutlichsten. Durch diese Aufgabenstellung
wird der Aufgabe der Charakter der Stochastik genommen. Im Vergleich zum Modellierungskreislauf wird deutlich, dass die Übergänge von der Realität zum Modell nicht eindeutig herausgestellt werden. Sowohl das Mathematisieren als auch das Anwenden/ Interpretie89
ren/ Validieren werden überhaupt nicht beachtet. Dies zeigt sich auch daran, dass die berechneten Werte an keiner Stelle reflektiert werden sollen. Beispielsweise könnte der Erwartungswert im frequentistischen Modell als der Wert interpretiert werden, zu dem die Mittelwerte stochastisch konvergieren. Unsicherheit, die sich in der Stochastik besonders in den
Wahrscheinlichkeitsmodellen ausdrückt, darf es anscheinend in der Mathematik und in Abituraufgaben erst Recht nicht geben.343 Doch nur wenn die Unsicherheit in Datensätzen akzeptiert wird und sich in (Abitur-)Aufgaben widerspiegelt, können die Schüler einen sinnvollen Umgang mit Daten erlernen.
5. Fazit
Die Briefwechsel Pascals und Fermats über das Teilungsproblem und die sogenannte „Wette
des Chevalier de Méré“ wird oft als die „Geburt der Wahrscheinlichkeitstheorie“ bezeichnet.
Fermat und Pascal entwickelten zum ersten Mal einen allgemeingültigen, theoretischen Lösungsweg, der auf ähnliche Probleme in der Glückspielwelt übertragen werden konnte. Sie
verwendeten dabei den sogenannten Laplace-Wahrscheinlichkeitsbegriff. In diesem nach
Laplace benannten Wahrscheinlichkeitsmodell können die Wahrscheinlichkeiten durch den
Quotient von günstigen und möglichen Fällen berechnet werden (P(E):=
Anzahl der Elemente von E
Anzahl der Elemente von Ω
=
Günstige
|E|
|Ω|
=
). Um diese Formel anzuwenden, müssen alle Fälle gleich-
Mögliche
wahrscheinlich und die Ergebnismenge endlich sein. Für eine unendliche Ergebnismenge
kann keine Laplace-Wahrscheinlichkeit berechnet werden. Allerdings kann mit Hilfe des
geometrischen Wahrscheinlichkeitsbegriffs eine Laplace-ähnliche Situation hergestellt werden und somit über die Flächenbetrachtung kontinuierliche Wahrscheinlichkeitsmengen behandelt werden.
Mit dem Einsetzen der Statistik im 17. Jahrhundert verlor das Modell der Gleichwahrscheinlichkeit seine Allgemeingültigkeit. Es rückte immer mehr die Frage nach der Verbindung
zwischen der relativen Häufigkeit und der Wahrscheinlichkeit in den Vordergrund. Bereits
zu dieser Zeit verwendeten die Menschen das empirische Gesetz der großen Zahlen, bei dem
sich die relativen Häufigkeiten bei genügend großer Versuchsanzahl um die Wahrscheinlichkeit stabilisieren. Bei diesem „Naturgesetz“ bleibt allerdings unklar, was eine genügend
große Versuchszahl ist und was stabilisieren bedeutet. Bernoulli konnte diese Aussage im
weitergehenden schwachen Gesetz der großen Zahlen präzisieren und wandte es auf statistische Fragestellungen an. Von Mises versuchte noch einen Schritt weiter zu gehen und die
343
Biehler: Gesetze, S. 16.
90
Wahrscheinlichkeit als analytischen Grenzwert der relativen Häufigkeit zu definieren. Dies
scheiterte jedoch, da lediglich eine stochastische Konvergenz im Sinne des schwachen Gesetzes der großen Zahlen nachgewiesen werden kann. Die Herangehensweise die Statistik,
als Ausgangspunkt für die Beschreibung der Wahrscheinlichkeitstheorie zu verwenden, wird
mit dem frequentistischen Wahrscheinlichkeitsbegriff bezeichnet.
Voraussetzung für den frequentistischen Wahrscheinlichkeitsbegriff ist also eine theoretisch
unendlich oft wiederholbare Anzahl an Zufallsversuchen sowie die Unabhängigkeit der einzelnen Versuche. Im Alltag wird der Begriff „Wahrscheinlichkeit“ jedoch viel breiter verwendet. Oftmals werden Bewertungen mit „mehr“ oder „weniger wahrscheinlich“ getroffen,
die qualitativ und stets subjektiv sind. Allerdings nähern sich die einzelnen subjektiven Meinungen mit einer wachsenden Menge an Daten immer stärker an. Diese Tatsache wird mit
dem „Lernen aus Erfahrung“ bezeichnet, dessen mathematische Grundlage der Satz von
Bayes ist. Diese Art der Auffassung, in der die Intuition der Ausgangspunkt einer Wahrscheinlichkeitsschätzung ist, drückt der subjektive Wahrscheinlichkeitsbegriff aus. Dieser
steht gleichberechtigt neben dem Laplace- und frequentistischen Wahrscheinlichkeitsbegriff. Insbesondere durch die Gegenüberstellung des Satzes von Bayes und des klassischen
Hypothesentests werden die unterschiedlichen Vorgehensweisen des frequentistischen und
des subjektiven Wahrscheinlichkeitsbegriffs deutlich und bilden gleichberechtigte Möglichkeiten bei der Entscheidung über Hypothesen.
Allerdings konnte der subjektive Wahrscheinlichkeitsbegriff, wie auch der Laplace- und frequentistische Wahrscheinlichkeitsbegriff nicht definieren, was Wahrscheinlichkeiten im mathematischen Sinne sind. Dies leistete erst der axiomatische Wahrscheinlichkeitsbegriff von
Kolmogorov, der sich komplett von der Anschauung löste und lediglich unbestimmte Beziehungen forderte. Dabei sind seine aufgestellten Axiome nicht beliebig, sondern spiegeln die
Gemeinsamkeiten der inhaltlich geprägten Wahrscheinlichkeitsbegriffe (Nichtnegativität,
Additivität und Normiertheit) wider. Diese Verbindung und der gleichzeitige fundamentale
Unterschied zwischen den inhaltlichen Wahrscheinlichkeitsbegriffen und der Axiomatik
sind notwendig, um die Schwierigkeiten der inhaltlichen Wahrscheinlichkeitsbegriffe (kontinuierliche Mengen und stochastische Konvergenz) zu beheben.
Das Axiomensystem erleichtert also das Rechnen mit Wahrscheinlichkeiten. Es löst allerdings nicht das Problem, dass die Realität in ein mathematisches Modell überführt werden
muss, um die mathematischen Ergebnisse zu interpretieren. Daher sind für die Modellierung
einer realen Situation die inhaltlichen Wahrscheinlichkeitsbegriffe unabdingbar. Es müssen
also die Chancen und Risiken der inhaltlichen Wahrscheinlichkeitsbegriffe bekannt sein.
91
Dabei wird deutlich, dass mit der Modellierung der Realität eine Unsicherheit miteinhergeht.
Der spöttisch gemeinte Spruch „In der Stochastik geht man von Unsicherheiten aus und berechnet neue Unsicherheiten“ trifft das Wesen der Stochastik. Dies wird verdeckt, wenn der
Fokus auf das Wahrscheinlichkeitskalkül gelegt wird. Vielmehr müssen die Schüler und
auch Erwachsene lernen, mit dieser Unsicherheit umzugehen. Die Stochastik kann keine absolute Gewissheit oder Wahrheit garantieren. Allerdings zeigen sowohl der Lehrplan als
auch die abschließend betrachtete Abituraufgabe, dass der Umgang mit Unsicherheit kaum
gefördert und gefordert wird. Durch die Analyse der einzelnen Wahrscheinlichkeitsbegriffe
und durch die starke Betonung des Modellierungseffekts kann der Umgang mit Unsicherheit
gefördert werden. Durch die Umstrukturierung (vgl. Tabelle 13), in der die Wahrscheinlichkeitsbegriffe als Schlüssel zur Stochastik verwendet werden und dem damit einhergehenden
Einbezug von kontinuierlichen Mengen, der stochastischen Konvergenz und der Beseitigung
des Schattendaseins der bedingten Wahrscheinlichkeit, können die Schüler im Mathematikunterricht zu mündigen Bürgern erzogen werden, die „Kompetenzen für den kritischen Umgang mit Daten, Chancen und Risiken“344 erlernt haben. Statt dem vorgeschlagenen Ablauf
des Lehrplans zu folgen, sollte daher das folgende Vorgehen345 beachtet werden, um den
Schülern die Beschäftigung mit der Unsicherheit im Mathematikunterricht zu ermöglichen:
Tabelle 13: Eigener Lehrplan.
Ziele/Inhalte (Sachund Methodenkompetenz)
1) Wahrscheinlichkeiten bestimmen und
in
Sachzusammenhangen interpretieren.
2) Wahrscheinlichkeiten mit Hilfe des
Laplace-Wahrscheinlichkeitsmodells bestimmen.
Hinweise zur Unterrichtsgestaltung
und Methodenkompetenz
Der Schwerpunkt liegt auf der Entwicklung eines inhaltlichen Verständnisses der
Wahrscheinlichkeitsbegriffe. Wahrscheinlichkeiten können demnach mit Hilfe des
Prinzips des unzureichenden Grundes (Laplace-Wahrscheinlichkeitsbegriffs), des
empirischen Gesetzes der großen Zahlen (frequentistischer Wahrscheinlichkeitsbegriff) und über die Intuition (subjektiver Wahrscheinlichkeitsbegriff) bestimmt
werden.
Zufallsexperimente durch ihre Ergebnismengen beschreiben.
Die Schüler/innen sollen das Prinzip des unzureichenden Grundes vertiefen und
die Bedeutung der Gleichwahrscheinlichkeit der Elementarereignisse erkennen.
Dabei soll die Grenze des Laplace-Wahrscheinlichkeitsbegriffs bei unendlichen
Ergebnismengen erkannt werden.
Die Berechnungsstrategie von Laplace-Wahrscheinlichkeiten durch die Formel
Günstige
soll behandelt werden. Dabei können systematische Abzählverfahren verMögliche
3) Wahrscheinlichkeiten mit Hilfe des
frequentistischen
wendet werden; eine ausführliche Behandlung kombinatorischer Regeln ist nicht
intendiert.
Intuitive Rechenregeln wie z.B. Pfadregeln (Summe, Produkt), Wahrscheinlichkeit
des Gegenereignisses, Wahrscheinlichkeit der Vereinigungsmenge von Ereignissen kennen und anwenden können.
Verbindung zur Datenanalyse schaffen und die Begriffe „Mermal“, „Empirische
Häufigkeitsverteilung“, „relative Häufigkeit“, „arithmetisches Mittel“ und „Standardabweichung wiederholen“.
344
Biehler: Daten und Zufall, S. 5.
Hierbei wurde sich stark am Lehrplan orientiert, sodass einige Formulierungen übernommen wurden. Daher
werden an dieser Stelle im Gegensatz zum Rest der Arbeit keine Operatoren verwendet.
345
92
Wahrscheinlichkeitsmodells bestimmen.
4) Wahrscheinlichkeiten mit Hilfe des
subjektiven
Wahrscheinlichkeitsmodells bestimmen.
5) Wahrscheinlichkeiten mit Hilfe des
axiomatischen Wahrscheinlichkeitsmodells bestimmen.
Das empirische Gesetz der großen Zahlen soll vertiefend behandelt werden. Die
großen Schwankungen der relativen Häufigkeiten zu Beginn einer Versuchsreihe
und die „Stabilisation der relativen Häufigkeiten bei genügend großer Versuchszahl“ soll analysiert werden. Die wacklige Konvergenz der relativen Häufigkeit
1
(stochastische Konvergenz) und die Faustregel des -Gesetz sollen thematisiert
√n
werden. Dabei bieten sich Simulationen an.
Der Begriff der Unabhängigkeit von Zufallsexperimenten kennen und anwenden
können. Er soll als Voraussetzung für den frequentistischen Wahrscheinlichkeitsbegriffs erkannt werden.
„Die Begriffe ‚Bernoullikette‘, ‚Binomialverteilung‘ verstehen und die Formel zur
Berechnung der Werte einer Binomialverteilung herleiten. Die Formeln für Erwartungswert und Standardabweichung einer Binomialverteilung kennen und anwenden.“ 346
Den Begriff der bedingten Wahrscheinlichkeit kennen und anwenden können.
Die Intuition als Ausgangspunkt zur Bestimmung von Wahrscheinlichkeiten erkennen und mit dem Lernen aus Erfahrung verbinden. Den Satz von Bayes als Werkzeug zur Mathematisierung des Lernens aus Erfahrung erkennen.
Die intuitiven Fehleinschätzungen zur bedingten Wahrscheinlichkeiten kennen.
Das natürliche Häufigkeitskonzept zur Hilfe im Umgang mit bedingten Wahrscheinlichkeiten kennen und anwenden können.
Ein Vergleich der unterschiedlichen Vorgehensweisen von subjektiven und objektiven Wahrscheinlichkeitsmodellen soll zur Vorbereitung der beurteilenden Statistik dienen.
Die unterschiedliche Vorgehensweise der Axiomatik erkennen und die Vor- und
Nachteile dieser Arbeitsweise einschätzen können.
Die Erweiterung der Wahrscheinlichkeitsräume auf kontinuierliche Mengen soll
angedeutet werden. Hierbei soll ein Rückbezug auf das Laplace-Modell vollzogen
werden.
„Die Begriffe ‚Zufallsgröße‘ und ‚Wahrscheinlichkeitsverteilung‘ kennen und an
Beispielen erläutern. Die Begriffe ‚Erwartungswert‘, ‚Varianz‘ und ‚Standardabweichung‘ einer Zufallsvariable kennen und anwenden.“347 Hierbei bietet sich eine
Verbindung zum frequentistischen Wahrscheinlichkeitsbegriff an.
Das schwache Gesetz der großen Zahlen beweisen und die mathematische Entspre1
chung des -Gesetzes aufstellen.
√n
Quelle: Eigene Konzeption.
Auf dieser Basis können die Probleme, die beim Übergang zur Normalverteilung entstehen,
vorgebeugt werden. Durch diese Änderungen in der Vorgehensweise kann der Lehrplan den
Anspruch erfüllen, den er sich selbst im ersten Satz stellt:
„Zentrales Anliegen dieses Themenbereichs [Stochastik] ist es, die Schülerinnen und Schüler mit Denkweisen und Verfahren der Stochastik vertraut zu machen. Dabei steht auch im Leistungskurs der Anwendungsbezug und nicht der Aufbau einer mathematischen Theorie im Mittelpunkt.“ 348
346
Mathea: Lehrplan Mathematik, S. 54.
Ebd. S. 54.
348
Ebd. S. 53.
347
93
Sind Menschen gute Statistiker?
6. Anhang
6.1 Arbeitsblätter
Bearbeiten Sie die Stationen intuitiv. Die Aufgaben werden im Laufe der Reihe wieder aufgegriffen und analysiert.
Station 1:349
a) Was ist wahrscheinlicher: 20-mal hintereinander bei einer (Laplace-)Münze Wappen zu
würfeln oder einen 6er im Lotto zu tippen (ohne Super-Zahl)?
b) Was ist wahrscheinlicher: 10-mal hintereinander eine 6 zu würfeln oder einen 6er im
Lotto (ohne Super-Zahl) zu tippen.
c) Welche der folgenden Münzwurfreihen ist am wahrscheinlichsten?
A: Kopf – Kopf – Kopf – Zahl – Zahl – Zahl
B: Zahl – Zahl – Zahl – Zahl – Zahl – Zahl
C: Kopf – Zahl – Kopf – Kopf – Zahl – Kopf
d) Auf einer Geburtstagparty treffen sich 30 Personen. Wie wahrscheinlich ist es, dass 2
Personen am gleichen Tag Geburtstag350 haben?
Station 2:351
a) Was halten Sie für wahrscheinlicher? Kreuzen Sie an!
○ (1) Mindestens 7 von 10 Neugeborenen in einem Krankenhaus sind Mädchen.
○ (2) Mindestens 70 von 100 Neugeborenen in einem Krankenhaus sind Mädchen.
○ (1) und (2) sind gleichwahrscheinlich.
b) Ist es als Roulette-Spieler sinnvoll sich die vorherigen Kugelziehungen anzuschauen?
Würden Sie einem Roulette-Spieler raten, nach 10-maligen Rot im nächsten Versuch auf
Schwarz zu setzen? Ändert sich Ihr Ratschlag für das Spiel Black-Jack, falls mehrere
Karten bekannt sind?
349
Aufgabe in modifizierter Form übernommen aus Strick: Vorstellungen, S. 53
Berücksichtige bei der Rechnung keine Schaltjahre.
351
Aufgabe in modifizierter Form übernommen aus Büchter; Henn: Elementare Stochastik, S. 176, 208.
350
96
Sind Menschen gute Statistiker?
c) Nehmen Sie Stellung zu folgenden (nicht ernst gemeinten) Aussagen:
-
Ein Flugreisender, der Angst vor Attentaten hat, sollte stets eine Bombe mit sich
führen. Die Wahrscheinlichkeit, dass gleichzeitig zwei Bomben an Bord sind, ist
fast Null!
-
Der Arzt eröffnet dem Patienten nach der Untersuchung: ,,Also, die Lage ist ernst.
Sie sind sehr krank; statistisch gesehen überleben 9 von 10 Menschen diese Krankheit nicht.“ Der Patient erbleicht. „Sie haben aber Glück“, beruhigt der Arzt. „Ich
hatte schon neun Patienten mit den gleichen Symptomen, und die sind alle tot.“
Station 3:
a) Das Taxiproblem352
Ein Taxi war an einem nächtlichen Verkehrsunfall mit Fahrerflucht beteiligt. In der Stadt, in
der der Unfall passierte, gibt es zwei Taxiunternehmen, eines mit grünen und eines mit
blauen Taxis. Folgende Daten sind nun gegeben: (i) 85% aller Taxis in der Stadt sind blau,
die anderen 15% sind grün. (ii) Ein Zeuge identifizierte das davonfahrende Taxi als „grün“.
Das Gericht untersuchte nun die Fähigkeit des Zeugen, die Farbe eines Taxis bei Nacht richtig zu identifizieren. In der Versuchsreihe (die Hälfte der Taxis war blau, die andere Hälfte
war grün), konnte der Zeuge beide Farben zu 80% richtig identifizieren, aber zu 20% irrte
er. Schätzen Sie, wie groß die Wahrscheinlichkeit ist, dass das Unfalltaxi wirklich grün und
nicht blau war?
b) Das Ziegenproblem353
Sie nehmen an einer Spielshow im Fernsehen teil, bei der Sie eine von drei verschlossenen
Türen auswählen sollen. Hinter einer der Türen wartet der Preis, ein Auto, hinter den beiden
anderen stehen Ziegen. Sie zeigen auf eine Tür, sagen wir Nummer eins. Sie bleibt vorerst
geschlossen. Der Moderator weiß, hinter welcher Tür sich das Auto befindet; mit den Worten: ‚Ich zeige Ihnen mal was‘ öffnet er eine andere Tür, zum Beispiel Nummer drei, und
eine meckernde Ziege schaut ins Publikum. Er fragt: ‚Bleiben Sie bei Nummer eins, oder
wählen Sie Nummer zwei?“
352
353
Aufgabe in modifizierter Form übernommen aus Kahneman; Tversky: On the Psychology, S. 241.
Aufgabe in modifizierter Form übernommen aus Zimmermann; Gundlach: Wie Ziegen, S. 316.
97
Sind Menschen gute Statistiker?
c) Das Kästchenparadoxon Bertrands 354
Drei zweigeteilte Schubladen enthalten in jedem Teil eine Münze. Man kann sie nach rechts
oder nach links jeweils zur Hälfte herausziehen und sieht dann die eine Münze. Eine enthält
zwei Goldmünzen, eine zwei Silbermünzen und die letzte eine Silber- und eine Goldmünze.
Sie ziehen eine Schublade halb heraus und sehen eine Goldmünze. Schätzen Sie die Wahrscheinlichkeit, dass hinter dem zweiten Teil der Münze eine silberne Münze steckt.
d) Der Fall Sally Clark355
Auf der Basis des DNA-Profils der am Tatort an der Leiche gefundenen Blutspur erstellte
der Sachverständige Dr. K. ein Gutachten, in dem er zu Protokoll gab, dass in einer Stadt
von der Größe Berlins ungefähr eine Million Männer als mögliche Täter in Frage kommen.
Im Falle der Schuld des Angeklagten zeigt die verwendete DNA-Analyse mit an Sicherheit
grenzender Wahrscheinlichkeit eine Übereinstimmung des DNA-Profils des Angeklagten
mit dem in der Blutprobe an der Leiche sichergestellten genetischen Fingerabdruck. Die
Wahrscheinlichkeit, dass der genetische Fingerabdruck eines Unschuldigen rein zufällig mit
dem DNA-Profil übereinstimmt, das in der Blutprobe an der Leiche gefunden wurde, beträgt
0,0001%. Im vorliegenden Fall stimmt das DNA-Profil der DNA-Probe des Angeklagten
mit dem DNA-Profil der am Tatort gefundenen Spur überein.
Stellen Sie sich vor, Sie sind Richter und müssen nun die Aussagekraft der gefundenen
DNA-Übereinstimmung bewerten: Mit welcher Wahrscheinlichkeit ist der Angeklagte tatsächlich Verursacher der am Tatort sichergestellten Spur? Mit welcher Wahrscheinlichkeit
ist er der Mörder?
354
355
Aufgabe in modifizierter Form übernommen aus Bartz: Denkfallen vermeiden, S. 32.
Aufgabe in modifizierter Form übernommen aus Schrade: Schwierigkeiten, S. 88.
98
Der Einstieg in die Stochastik
Aufgabe 1: Der Riemer-Würfel356
In der unten abgebildeten Grafik sind zwei Würfel zu sehen. Einer der beiden ist ein gewöhnlicher Spielwürfel, der andere ein Quaderwürfel357.
a) Schätzen Sie für beide Würfel vor dem Werfen die Wahrscheinlichkeit dafür, dass beim
einfachen Werfen der Würfel eine bestimmte Augenzahl fällt. Tragen Sie Ihre Schätzungen in die untenstehende Tabelle ein. Begründen Sie, wie Sie auf Ihre Einschätzung gekommen sind.
Augenzahl
Gewöhnlicher Würfel
Quader-Würfel
1
2
3
4
5
6
b) Diskutieren Sie, ob und wenn ja wie Sie Ihre Schätzungen verbessern können. Tragen
Sie diese (möglicherweise verbesserten) Schätzungen in die untenstehende Tabelle ein.
Augenzahl
Gewöhnlicher Würfel
Quader-Würfel
1
2
3
4
5
6
356
Aufgabe in modifizierter Form übernommen aus Eichler; Vogel: Leitidee Daten und Zufall, S. 147.
Der Mathematikdidaktiker Wolfgang Riemer benutzte diesen als Erster im Mathematikunterricht. Daher
wird dieser auch öfter als Riemer-Quader bezeichnet.
357
99
Der Einstieg in die Stochastik
Aufgabe 2: Die „Geburt“ der Stochastik – Die Wette des Chavalier de Méré358
Der Chevalier de Méré war ein leidenschaftlicher Spieler und lebte im Frankreich des 17. Jahrhunderts. Eines der Spiele, mit denen er seine Mitspieler verführte, war das folgende: „Wir werfen einen Würfel viermal. Wenn dabei eine
oder mehrere Sechsen sind, gewinne ich. Wenn keine Sechs dabei ist, gewinnen
Sie.“ Soweit wir wissen, waren seine Würfel fair; dennoch gewann der Chevalier mit diesem
Spiel regelmäßig Geld. Schließlich fand er keine Opfer mehr, oder das Spiel wurde auf die
Dauer eintönig - was immer der Grund war, er dachte sich eine Variante aus, die ebenso
lukrativ sein sollte. Hier ist das neue Spiel, das der Chevalier seinen Mitspielern anbot: Wir
werfen ein Paar von Würfeln 24 Mal. Wenn dabei eine Doppel-Sechs oder mehrere sind,
gewinne ich. Wenn keine Doppel-Sechs dabei ist, gewinnen Sie.
a) Würden Sie das Angebot des Chevaliers annehmen?
b) Erklären Sie, wie der Chevalier auf die Vermutung kam, dass er auch mit dieser Wette
gewinnt.
c) Nach ein paar Spielen bemerkte der Chevalier allerdings, dass er öfter verlor als gewann.
Was könnte er tun, um zu entscheiden, ob seine Intuition (höhere Gewinnwahrscheinlichkeit) oder seine Erfahrung (niedrigere Gewinnwahrscheinlichkeit) richtig ist?
Aufgabe 3: Die Wahrscheinlichkeitsbegriffe
a) Untersuchen Sie in Aufgabe 1 und Aufgabe 2, auf welche Art und Weise wir Wahrscheinlichkeiten bestimmen können.
b) Diskutieren Sie, welche Möglichkeiten aber auch Grenzen die Wahrscheinlichkeitsbegriffe haben. Welche Fragen bleiben noch offen?
Wahrscheinlichkeitsbegriffe
Möglichkeiten
Grenzen
Offene Fragen
Vertiefung: Die „Geburt“ der Stochastik – Die Wette des Chevalier de Méré
Überprüfen Sie mit Hilfe des frequentistischen Wahrscheinlichkeitsbegriffs die Vermutung
des Chevaliers.
358
Aufgabe in modifizierter Form übernommen aus Gigerenzer: Die Evolution, S. 2.
100
Der Laplace-Wahrscheinlichkeitsbegriff I - So berechne ich Laplace-Wahrscheinlichkeiten
Aufgabe 1: Die Wette des Chavalier de Méré (Fortsetzung)359
De Méré war sich immer noch unschlüssig, wie er sich entscheiden sollte. Daher
fragte er die zu dieser Zeit wohl bekanntesten Mathematiker seiner Zeit: Blaise
Pascal und Pierre de Fermat. Diese benutzten bei ihren Berechnungen im Grunde genommen das Laplace-Wahrscheinlichkeitsmodell.
Fermat
Pascal
a) Lösen Sie das Problem des Chevaliers mit Hilfe des Laplace-Wahrscheinlichkeitsmodells. Berechnen Sie zunächst die Wahrscheinlichkeit, dass der Chevalier gewinnt, wenn
er auf mindestens eine 6 in vier Würfeln setzt. Falls Sie nicht weiterkommen, stehen
Ihnen Hilfen zur Verfügung.
b) Fassen Sie zusammen, wie man mit Hilfe des Laplace-Wahrscheinlichkeitsbegriff Wahrscheinlichkeiten berechnen kann. Welchen Fehler machte de Méré in seinen theoretischen Überlegungen? Falls Sie noch keine Idee haben, lösen Sie zunächst Aufgabe 2.
359
Aufgabe in modifizierter Form übernommen aus Gigerenzer: Die Evolution, S. 2.
101
Der Laplace-Wahrscheinlichkeitsbegriff I - So berechne ich Laplace-Wahrscheinlichkeiten
Aufgabe 2: Das Werfen mit zwei Würfeln360
Beim Strategiespiel „Die Siedler von Catan“ würfelt jeder Spieler mit 2 Würfeln und addiert
die Augenzahlen. In diesem Spiel hat die Zahl 7 eine Sonderfunktion, da man mit ihr die
Rohstoffe eines Gegenspielers blockieren kann.
Spielfeld: Siedler von Catan
a) Schätzen Sie die Wahrscheinlichkeit, dass Sie eine 7 würfeln.
b) Bestimmen Sie die Laplace-Wahrscheinlichkeit, dass Sie eine 7 würfeln. Falls Sie nicht
weiterkommen, stehen Ihnen Hilfe zur Verfügung.
c) Beurteilen Sie die Vorgehensweise der Schüler aus Hilfe 3.
d) Berechnen Sie die Laplace-Wahrscheinlichkeit der restlichen Zahlen (2-12). Vergleichen Sie die Größen der Zahlen mit den Laplace-Wahrscheinlichkeiten der Kärtchen
(siehe Abbildung).
Merke: So berechne ich Laplace-Wahrscheinlichkeiten
360
Aufgabe in modifizierter Form übernommen aus Prediger: Auch will ich, S. 34.
102
Der Laplace-Wahrscheinlichkeitsbegriff I - So berechne ich Laplace-Wahrscheinlichkeiten
Aufgabe 3: Eigenschaften der Laplace-Wahrscheinlichkeit361
Beweisen Sie die Eigenschaften a) - f)!
Es liege ein Laplace-Experiment mit endlicher Ergebnismenge Ω = {ω1, ω2,…, ωn}
vor. Dann gilt für die Laplace-Wahrscheinlichkeiten der Ereignisse:
a) 0 ≤ P(E) ≤ 1 für alle E ⊆ Ω .
b) P(Ω) = 1; P(∅) = 0.
c) P(𝐸̅ ) = 1 − P(E) für alle E ⊆ Ω .
d) P(E1 ∪ E2) = P(E1) + P(E2) für alle E1,E2 ⊆ Ω mit E1∩E2 = ∅ .
e) P(E1 ∪ E2) = P(E1) + P(E2) − P(E1∩E2) für alle E1, E2 ⊆ Ω .
f) Speziell gilt: P(E) = ∑𝜔∈𝐸 𝑃({𝜔}) und P(Ω) = ∑𝜔∈𝛺 𝑃({𝜔})= ∑𝑛𝑖=1 𝑃({𝜔𝑖})= 1
Vertiefung: Schon wieder der Chevalier de Méré!362
Chevalier de Méré vermutete aufgrund theoretischer Überlegungen, dass beim gleichzeitigen Werfen dreier symmetrischer (unterscheidbarer) Spielwürfel die Chancen für das Auftreten der Augensumme 11 und der Augensumme 12 gleich groß sein müssen, denn sowohl
für die Augensumme 11 als auch für die Augensumme 12 gibt es jeweils sechs verschiedene
Möglichkeiten:
Augensumme 11: {(6, 4, 1), (6, 3, 2), (5, 5, 1), (5, 4, 2), (5, 3, 3), (4, 4, 3)}
Augensumme 12: {(6, 5,1), (6, 4, 2), (6, 3, 3), (5, 5, 2), (5, 4, 3), (4, 4, 4)}
a) Widerlegen Sie anhand der doppelt unterstrichenen Beispiele, warum de Mérés These
verworfen werden muss.
b) Berechnen Sie die Laplace-Wahrscheinlichkeit für die Augensumme 11 beziehungsweise Augensumme 12 beim Werfen dreier unterscheidbarer Würfel.
361
362
Aufgabe in modifizierter Form übernommen aus Büchter; Henn Elementare Stochastik, S. 168.
Aufgabe in modifizierter Form übernommen aus Kütting; Sauer; Padberg: Elementare Stochastik, S. 77.
103
Der Laplace-Wahrscheinlichkeitsbegriff I - So berechne ich Laplace-Wahrscheinlichkeiten
Aufgabe 1: Die Wette des Chavalier de Méré (Fortsetzung) - Hilfestellungen
a) Lösen Sie die Aufgabe des Chevaliers de Méré
Hilfe 1: Berechnen Sie zunächst die Wahrscheinlichkeit, dass der Chevalier das Spiel verliert. Warum ist es leichter dieses Problem zu lösen? Wie können wir daraus die Gewinnwahrscheinlichkeit des Chevaliers ableiten? Begründen Sie Ihre Antwort mit Hilfe der Eigenschaften der Laplace-Wahrscheinlichkeit aus Aufgabe 3.
Hilfe 2: Der Chevalier de Méré hat uns in seinen Überlegungen zur zweiten Wette schon
einen Tipp gegeben: Wie berechnet er die Wahrscheinlichkeit, dass eine Doppel-6 fällt?
Verallgemeinern Sie dieses Verfahren und berechnen Sie die Wahrscheinlichkeit, dass keine
6 in vier Würfen fällt.
Hilfe 3: Vervollständigen Sie folgenden Lückentext.
Wir wissen, dass die Laplace-Wahrscheinlichkeit
beträgt. Mit Hilfe der Eigenschaften der
Laplace-Wahrscheinlichkeit wissen wir, dass die Wahrscheinlichkeit keine 6 zu würfeln
(= 1 - ) beträgt. Es ist leichter dieses Problem zu lösen, weil ________________________.
Durch die Überlegungen des Chevaliers wissen wir, dass P(keine 6 in vier Würfen) =
∙ ∙
= . Daher wissen wir, dass die Gewinnwahrscheinlichkeit des Chevaliers
∙
(1 - )
beträgt.
104
Der Laplace-Wahrscheinlichkeitsbegriff I - So berechne ich Laplace-Wahrscheinlichkeiten
Aufgabe 2: Das Werfen mit zwei Würfeln - Hilfestellungen
a) Bestimmen Sie die Laplace-Wahrscheinlichkeit, dass Sie eine 7 würfeln.
Hilfe 1: Überlegen Sie, wie Sie die Wahrscheinlichkeit einer 6 bei der Wette des Chevaliers
bestimmt haben. Übertragen Sie dieses Prinzip auf die Aufgabe.
Hilfe 2: Wie hoch ist die Wahrscheinlichkeit, dass Sie beim Werfen eines Würfels eine gerade Zahl würfeln? Übertragen Sie dieses Prinzip auf die Aufgabe.
Hilfe 3: Betrachten Sie folgende Vorgehensweisen und entscheiden Sie, wer Recht hat.
Tim: Ich habe mir alle möglichen Zahlenpaare notiert: Ω1 = {(1,1), (1,2),…, (1,6), (2,2),
(2,3),…, (4,6), (5,5), (5,6), (6,6)}. Diese habe ich gezählt und komme auf 21 mögliche Ergebnisse. Da ich eine 7 würfeln möchte, betrachte ich die Tupel deren Addition 7 ergibt, das
heißt E1 = {(1,6), (2,5), (3,4)}. Das heißt die Wahrscheinlichkeit eine 7 zu würfeln, be3
trägt 21.
Lena: „Ich habe mir alle möglichen Zahlenpaare notiert. Dabei habe ich die Würfel unterschieden (zur Veranschaulichung benutzt Lena einen roten und einen blauen Würfel). Die
erste Komponente steht für den blauen Würfel und die zweite für den roten Würfel: Ω2 =
{(1|1), (1|2),…, (1|6), (2|1), (2|2),…, (5|5), (5|6), (6|1),... (6|6)}. Diese habe ich gezählt und
komme auf 36 mögliche Ergebnisse. Da ich eine 7 würfeln möchte, betrachte ich die Tupel
deren Addition 7 ergibt, das heißt E2 = {(1,6), (2,5), (3,4), (4,3), (5,2), (6,1)}. Das heißt die
6
Wahrscheinlichkeit eine 7 zu würfeln beträgt 36.“
Sarah: „Ich habe mir alle möglichen Summen notiert: Ω3 = {2, 3, 4,…, 10, 11, 12}. Um eine
7 zu würfeln, habe ich nur eine Möglichkeit: E3 = {7}. Das heißt die Wahrscheinlichkeit eine
7 zu würfeln, beträgt
1
“.
11
105
Der Laplace-Wahrscheinlichkeitsbegriff II – Kombinatorischer Exkurs
Aufgabe 1: Zählverfahren
Der Vater hat für seine vier Kinder bei einem Glückspiel mitgemacht und tatsächlich zwei
Freikarten für ein Bundesligaspiel gewonnen.363 Der Vater schreibt die Namen seiner Kinder
auf gleich große Zettel und steckt sie in einen Hut/ Urne. Welche Möglichkeiten hat der
Vater die Karten unter seinen Kindern zu verteilen?
Aufgabe 2: Kombinatorische Grundfiguren364
a) Ordnen Sie den Beispielen jeweils eine der erarbeiteten kombinatorischen Zählfiguren
(Ziehen mit Beachtung der Reihenfolge und mit Zurücklegen; Ziehen mit Beachtung der
Reihenfolge und ohne Zurücklegen; Ziehen ohne Beachtung der Reihenfolge und ohne
Zurücklegen) zu und berechnen Sie die Anzahl der Möglichkeiten die jeweiligen Scheine
auszufüllen.
Beispiel 1:
Das Fußball-Toto kam ab 1921 in England auf. Das Wort „Toto“ leitet sich ab vom Totalisator, einer Einrichtung zum Wetten in allen Wettarten auf der Pferderennbahn. In Deutschland wird seit 1948 die 11er Wette des Fußball-Totos gespielt. Bei dieser Wette müssen die
Spielausgänge von 11 Spielpaarungen, die den Toto-Spielern vorher bekannt sind, vorhergesagt werden. Je nach Vorhersage (Sieg der Heimmannschaft, Unentschieden oder Sieg der
Gastmannschaft) kreuzt man 1, 0 oder 2 an.
363
364
In den anderen Gruppen besitzt der Vater jeweils 5 Kinder und hat 3 bzw. 2 Freikarten gewonnen.
Aufgabe in modifizierter Form übernommen aus Büchter; Henn: Elementare Stochastik, S. 232.
106
Der Laplace-Wahrscheinlichkeitsbegriff II – Kombinatorischer Exkurs
Beispiel 2:
Bis vor Einführung der neuen Keno-Lotterie im Jahr 2004 gab es in Deutschland das Pferde
Rennquintett. Bei einer Wette mussten für ein Pferderennen, dessen 15 Teilnehmer den Spielern vorher bekannt waren, die drei besten Pferde vorhergesagt werden. Es waren also drei
Kreuze zu machen, wobei Ankreuzen in der oberen Reihe den 1. Platz vorhersagte, in der 2.
bzw. 3. Reihe dementsprechend den 2. bzw. 3. Platz.
Beispiel 3:
Das Lotto kam im 16. Jahrhundert auf. Das Wort stammt vom niederländischen lot (Los).
[…] Das deutsche Zahlenlotto „6 aus 49“ wurde 1952 in Berlin genehmigt und ab 1955 in
der BRD eingeführt. Bei diesem Lotto müssen auf einem Wettschein sechs der Zahlen 1,
2,…, 49 angekreuzt werden. Den ersten Gewinn erzielt der Tipper, wenn er drei Zahlen
richtig getippt hat; den Hauptgewinn, falls er alle sechs Zahlen korrekt getippt hat.
107
Der Laplace-Wahrscheinlichkeitsbegriff II – Kombinatorischer Exkurs
b) In der Realität werden die Beispiele mit verschiedenen Gewinnsystemen gespielt. Berechnen Sie für jedes Beispiel die gesuchten Laplace-Gewinnwahrscheinlichkeiten.
Beispiel 1: Erweiterung Fußball-Toto
Es gibt drei Gewinnklassen, die Klasse I mit 11, die Klasse II mit 10 und die Klasse III mit
9 richtigen Vorhersagen.
Beispiel 2: Erweiterung Pferderennen
Es gab zwei Gewinnklassen. In der ersten Klasse mussten die drei Gewinn-Pferde in der
richtigen Reihenfolge angekreuzt worden sein, in der zweiten Klasse mussten nur die 3 richtigen Pferde angekreuzt worden sein, die Reihenfolge spielte keine Rolle.
Erweiterung Beispiel 3: Erweiterung Lotto
In Deutschland wird das Lotto-Spiel in Gewinnklassen eingeteilt. Die Spieler können mit 3,
4, 5 oder 6 Richtigen gewinnen.
c) Beurteilen Sie, in welchen Beispielen das Laplace-Modell eine geeignete Annahme darstellt.
Zusatzaufgabe, falls Sie schon fertig seid:
Beim Lotto werden eigentlich zunächst zufällig sechs Gewinnzahlen, dann als siebte Zahl
die Zusatzzahl, gezogen. Berechnen Sie die Wahrscheinlichkeiten mit 3, 4, 5 oder 6 plus
Zusatzzahl.
108
Der Laplace-Wahrscheinlichkeitsbegriff II – Kombinatorischer Exkurs
Aufgabe 3: Das Teilungsproblem365
Ein Freund und Sie haben eine Reihe von Glücksspielen (Partien) abgemacht. Jede Partie
endet mit Gewinn oder Verlust. Es gibt kein Remis. Die Chancen für Sie sind gleich. Wer
zuerst insgesamt 5 Partien gewonnen hat, erhält die Einsätze. Durch höhere Gewalt muss
das Spiel beim Stand von 4:3 für Sie abgebrochen werden.
a) Beurteilen Sie, wie die Einsätze zu verteilen sind?
b) Beurteilen Sie die Lösungsvorschläge, die von den verschiedenen Mathematikern im
Laufe der Geschichte gemacht wurden (Infoblatt).
c) Übertragen Sie die Methode Fermats auf die folgende Problemstellungen:
-
Ein Freund und Sie ziehen abwechselnd aus einem Hut mit 10 Losen. Es gibt 9 Nieten und einen Hauptgewinn. Wer den Hauptgewinn zieht, hat gewonnen. Möchten
Sie anfangen?
-
Ein Freund und Sie drehen abwechselnd an diesem Glücksrad. Das rote Feld gewinnt. Möchtest Sie anfangen zu drehen?
Merke: Pfadregeln (intuitv)
365
Aufgabenteile a) und b) in modifizierter Form übernommen aus Kütting; Sauer; Padberg: Elementare
Stochastik, S. 79.
109
Der Laplace-Wahrscheinlichkeitsbegriff II – Kombinatorischer Exkurs
Infoblatt366
Fra Luca Pacioli (1445–1514), Franziskanermönch und Lehrer für Mathematik an verschiedenen italienischen Universitäten, geht vom realisierten Spielergebnis aus und sagt, es sei
im Verhältnis 4:3 aufzuteilen.
Niccolò Tartaglia (1499-1557), Mathematiklehrer in Venedig, hält von Paciolis Weg nichts:
Ein solches Problem soll eher juristisch als durch die Vernunft gelöst werden; denn egal, auf
welche Art und Weise man es löst, es gibt immer einen Grund zu streiten. Er schlägt aber
dennoch das Verhältnis (5+4−3):(5+3−4) = 3:2 vor.
Pascals Lösung ist folgende: Wenn B die nächste Partie gewinnen würde, wäre Gleichstand,
und B müsste die Hälfte des Einsatzes bekommen. Da die Chance zu gewinnen nur
1
2
ist,
1
gebührt ihm die Hälfte der Hälfte, also 4 der Einsätze, d. h. es ist im Verhältnis 3:1 zu teilen.
Fermat kommt unabhängig von Pascal zum selben Ergebnis. Fermat argumentiert so: Nach
spätestens zwei weiteren Partien ist entschieden, welcher der beiden Spieler Sieger ist. Es
gibt dann vier verschiedene Anordnungen für die Ausgänge der zwei noch zu spielenden
Partien. Die vier möglichen Resultate werden als gleich wahrscheinlich angesehen:
Sieg A
366
Sieg A
Sieg A
Sieg B
Infoblatt in modifizierter Form übernommen aus Kütting; Sauer; Padberg: Elementare Stochastik, S. 79.
110
Der Laplace-Wahrscheinlichkeitsbegriff III-Kontinuierliche Ergebnismengen
Aufgabe 1: Das Glücksrad
Ein Freund und Sie gehen auf einen Jahrmarkt. Auf diesem sehen ihr dieses Glücksrad. Das
rote Feld gewinnt.
a) Berechnen Sie die Laplace-Wahrscheinlichkeit zu gewinnen.
b) Untersuchen Sie die untenstehenden Fragestellungen über das Glücksrad, indem Sie die
Größe der Felder variieren.
-
Was passiert, wenn die Laplace-Felder unendlich klein werden?
-
Wie kann man Wahrscheinlichkeiten berechnen, wenn die Felder nicht gleich groß
sind?
Aufgabe 2: Anwendung des Laplace-Wahrscheinlichkeitsbegriffs
Überprüfen Sie Ihre intuitiven Vermutungen vom Arbeitsblatt („Sind Menschen gute Statistiker“) mit Hilfe des Laplace-Wahrscheinlichkeitsbegriffs.367
a) Was ist wahrscheinlicher: 20-mal hintereinander bei einer (Laplace-)Münze Wappen zu
würfeln oder einen 6er im Lotto zu tippen (ohne Super-Zahl)?
b) Was ist wahrscheinlicher: 10-mal hintereinander eine 6 zu würfeln oder einen 6er im
Lotto (ohne Super-Zahl) zu tippen.
c) Welche der folgenden Münzwurfreihen ist am wahrscheinlichsten?
A: Kopf – Kopf – Kopf – Zahl – Zahl – Zahl
B: Zahl – Zahl – Zahl – Zahl – Zahl – Zahl
C: Kopf – Zahl – Kopf – Kopf – Zahl – Kopf
d) Auf einer Geburtstagparty treffen sich 30 Personen. Wie wahrscheinlich ist es, dass 2
Personen am gleichen Tag Geburtstag368 haben?
367
Durch die Unterschiede zwischen objektiven und subjektiven Wahrscheinlichkeitswerten rückte die Fragestellung in den Fokus, ob die menschliche Intuition dem wahrscheinlichkeitstheoretischen Kalkül entsprechen
und inwiefern die Intuition durch gewisse Darstellungen unterstützt werden kann. Antworten auf diese Fragen
versuchte die psychologische Forschung seit Mitte des 20. Jahrhunderts zu erzielen. Insbesondere Kahneman
und Tversky erläuterten diese Frage in den 1970er Jahre. Besonders empfohlen wird an dieser Stelle
Kahneman: Schnelles Denken, Langsames Denken. München 2012.
368
Berücksichtige bei der Rechnung keine Schaltjahre.
111
Der Laplace-Wahrscheinlichkeitsbegriff III-Kontinuierliche Ergebnismengen
Aufgabe 3: Reflexion des Laplace-Wahrscheinlichkeitsbegriffs
a) Erläutern Sie folgende Zitate (I, II), indem Sie sie den Wahrscheinlichkeitsbegriffen zuordnen und das damit einhergehende Bild der Stochastik darstellen.
b) Fassen Sie zusammen, welche Probleme mit dem Laplace-Wahrscheinlichkeitsbegriff
gelöst werden konnten und bei welchen es Schwierigkeiten gab. Werten Sie aus, ob mit
Hilfe des Laplace-Ansatzes Wahrscheinlichkeiten definiert werden können.
I.
Nach dem Fermat und Pascal das Teilungsproblem mit dem gleichen Ergebnis gelöst
hatten, schrieb Pascal in einem Brief an Fermat: „Je vois bien, que la verité est la même
à Toulouse et à Paris.“
II.
Der Schweizer Mathematiker und Physiker Jakob Bernoulli
(1655-1705) schrieb in seinem Werk „Ars Conjunctandi“ (Kunst
des Vermutens)369: „Wir sind also dahingelangt, daß zur richtigen
Bildung von Vermutungen nichts anderes zu tun erforderlich ist,
als daß wir zuerst die Zahl der Fälle genau ermitteln und dann bestimmen, um wieviel
die einen Fälle leichter als die anderen auftreten können. Und hier schein uns gerade die
Schwierigkeit zu liegen, da nur für die wenigsten Erscheinungen und fast nirgends als in
Glücksspielen möglich ist; […] Welcher Sterbliche könnte aber je die Anzahl der der
Krankheiten, welche den menschlichen Körper an allen seinen Teilen und in jedem Alter
befallen und den Tod herbeiführen können, ermitteln und angeben, um wie viel leichter
diese als jene Krankheit, die Pest als die Wassersucht, die Wassersucht als Fieber den
Mengen zugrunde richtet, um daraus eine Vermutung über das Verhältnis von Leben und
Sterben künftiger Generationen abzuleiten […] Aber ein anderer Weg steht uns hier offen, um das Gesuchte zu finden und das, was wir a priori nicht bestimmen können, wenigstens a posteriori, d.h. aus dem Erfolge, welcher bei ähnlichen Beispielen in zahlreichen Fällen beobachtet wurde, zu ermitteln.“370
Vertiefung: Eigenschaften der relativen Häufigkeiten
Schlagen Sie in Ihren Unterlagen aus der Sek. I die Eigenschaften der relativen Häufigkeiten
nach. Vergleichen Sie diese mit den Eigenschaften der Laplace-Wahrscheinlichkeit.
Mit seinem Werk „Ars Conjectandi“, das posthum 1713 publiziert wurde, trug er wesentlich zur Entwicklung der Stochastik bei. Insbesondere interessierte ihn die Verbindung zwischen relativer Häufigkeit und Wahrscheinlichkeit.
370
Steinbring: Zur Entwicklung, S. 33.
369
112
Der frequentistische Wahrscheinlichkeitsbegriff I – Das empirische Gesetz der großen Zahlen
Aufgabe 1: Warum gibt es immer so wenige rote Gummibärchen in der Tüte?371
a) Stellen Sie eine Prognose auf, wie viele rote Gummibärchen in einer Packung sind.
b) Beurteilen Sie, wie viele Packungen für eine Prognose geöffnet werden müssen. Bestimmen Sie mit Hilfe der Datenanalyse eine Wahrscheinlichkeit für rote Gummibärchen in
einer Packung. Kann Ihre Hypothese aus Aufgabenteil a) beibehalten werden?
c) Können Sie mit Hilfe der Datenanalyse noch weitere Prognosen angeben?
Aufgabe 2: Ein Test ohne gelernt zu haben372
Wir schreiben einen Chinesisch-Test373, bei dem Sie das deutsche Wort ins Chinesische
übersetzen müssen. Dabei werden Ihnen jeweils zwei Antwortmöglichkeiten gegeben. Wenn
Sie 70% der Aufgaben richtig lösen, haben Sie den Test bestanden.
Sie dürfen auswählen, ob Sie den Test

mit 10 Fragen
oder

mit 50 Fragen
ausführen wollen.
a) Entscheiden Sie sich zunächst für eine Testform und lösen Sie den Test. Modellieren Sie
die Situation anschließend mit einem Münzwurf. Beurteilen Sie diese Form der Modellierung für einen Multiple-Choice-Test mit zwei Antwortmöglichkeiten.
b) Nehmen Sie Stellung zu folgenden Aussagen, indem Sie eine Computersimulation verwenden.
-
Es ist wahrscheinlicher beim 10-fachen Münzwurf mindestens 7-mal „Wappen“ als
beim 50-fachen Münzwurf mindestens 35-mal „Wappen“ zu werfen.
-
Das empirische Gesetz der großen Zahlen besagt, dass die relativen Häufigkeiten
mit zunehmender Versuchszahl „immer näher“ an die Laplace-Wahrscheinlichkeit
kommen.
371
Aufgabe in modifizierter Form übernommen aus Eichler; Vogel: Leitidee Daten und Zufall, S. 159.
Aufgabe in modifizierter Form übernommen aus Lergenmüller: Mathematik Neue Wege, S. 23.
373
Dieser steht für einen Test, bei dem die Schüler keine Präferenz für eine der beiden Antwortmöglichkeiten
haben. Deshalb wird dieser Test an dieser Stelle auch nicht erstellt.
372
113
Der frequentistische Wahrscheinlichkeitsbegriff I – Das empirische Gesetz der großen Zahlen
c) Der Mathematiker Richard von Mises hatte 1919 die Idee die Wahrscheinlichkeit als analytischen Grenzwert der relativen Häufigkeit zu definieren.
Von Mises
Ordnen Sie die einzelnen Sätze. Beurteilen Sie anschließend die Idee von Mises.
so dass |P(E) –hm(E) < ɛ| für alle m≤mɛ.
Wenn für ein Ereignis E eine reelle Zahl P(E) existiert,
sogenannten ɛ-Schlauch P(E)±ɛ hineinlaufen,
dann müsste für jede positive Zahl ɛ eine positive Zahl mɛ existieren
Aber genau das kann man nicht garantieren.
aber kann ihn auch wieder verlassen
Denn nach der Wahl eines ɛ>0 wird die relative Häufigkeit
für die P(E) = lim hm (E) gilt,
m→∞
114
Der frequentistische Wahrscheinlichkeitsbegriff I – Das empirische Gesetz der großen Zahlen
Aufgabe 3: Wie gut kann ich einem gefundenen Schätzwert vertrauen?374
Angenommen die Wahrscheinlichkeit von Wappen bei einer Münze beträgt 0,5. In Aufgabe
2 haben wir gesehen, dass die relative Häufigkeit um den Wert 0,5 „streut“.
a) Füllen Sie folgende Tabelle mit Hilfe einer Computersimulation aus.
N
25
100
400
1000
Relative Häufigkeit
Intervall für h (im Plenum)
Faustregel für Prognoseintervalle (p=0,5; 95%):
b) Eine Münze soll 200-mal geworfen werden. Schätzen Sie die Größe des Prognoseintervalls. Berechnen Sie anschließend das Prognoseintervall, in das mit 95% Sicherheit die
relative Häufigkeit fällt.
c) Schätzen Sie, wie oft Sie eine Münze werfen müssen, damit die relative Häufigkeit für
Wappen mit einer Sicherheit von 95% im Intervall [0,48; 0,52] liegt. Berechnen Sie anschließend die Anzahl der Würfe.
374
Aufgabe in modifizierter Form übernommen aus Lergenmüller: Mathematik Neue Wege, S. 33.
115
Der frequentistische Wahrscheinlichkeitsbegriff I – Das empirische Gesetz der großen Zahlen
Vertiefung: Verbindung relative Häufigkeit und Wahrscheinlichkeit
a) Erinnern Sie sich an die Wette der Chevaliers. In dieser hatten wir die Laplace-Wahrscheinlichkeit für mindestens eine 6 aus vier Würfeln beziehungsweise mindestens eine
Doppel-Sechs in 24 Würfeln berechnet. Konnte der Chevalier mit 5000 Spielen herausfinden, ob die jeweilige Wette von Vorteil ist?
Hinweis:
Statt dem
p±
1
-Gesetz verwendet man bei einer Wahrscheinlichkeit p≠0,5 die Formel
√n
2√p∙(p−1)
1
√n
√n
. Begründen Sie, warum das
-Gesetz ein Spezialfall dieser Formel darstellt.
b) Nehmen Sie Stellung zu folgender Aussage Jakob Bernoullis aus seinem Werk „Ars conjunctandi“:
„Man muss vielmehr noch Weiteres in Betracht ziehen, woran vielleicht niemand bisher
auch nur gedacht hat. Es bleibt nämlich noch zu untersuchen, ob durch Vermehrung der
Beobachtungen das wahre Verhältnis erreicht, und zwar in dem Maße, dass diese Wahrscheinlichkeit schließlich jedem beliebigen Grad der Gewissheit übertrifft, oder ob das
Problem vielmehr, sozusagen, seine Asymptote hat, d.h. ob ein bestimmter Grad der Gewissheit, das wahr Verhältnis der Fälle gefunden zu haben, vorhanden ist, welcher auch
bei beliebiger Vermehrung der Beobachtungen niemals überschritten werden kann.“375
375
Lergenmüller: Neue Wege, S. 33.
116
Der frequentistische Wahrscheinlichkeitsbegriff II – Der Begriff der Unabhängigkeit
Aufgabe 1: Abhängigkeit und Unabhängigkeit von Ereignissen
a) Geben Sie an, welchen Wahrscheinlichkeitsbegriff der Systemanalytiker verwendete.
Erläutern Sie, welchen Fehler er in seiner Argumentation machte.
b) Betrachten Sie auf dem Arbeitsblatt „Der Laplace-Wahrscheinlichkeitsbegriff II“ die
Aufgabe 3c). Prüfen Sie, welche Aufgabe mit dem frequentistischen Wahrscheinlichkeitsbegriff gelöst werden kann.
Definition: Stochastische Unabhängigkeit von zwei Ereignissen
Aufgabe 2: Der gefärbte Tetraeder von Serge N. Bernstein (1880 – 1968)376
Von den vier Flächen eines Tetraeders sei eine rot, eine blau, eine grün und die vierte Fläche
mit allen drei Farben bemalt. Es seien R: das Tetraeder fällt auf eine Fläche mit roter Farbe,
B: das Tetraeder fällt auf eine Fläche mit blauer Farbe, G: das Tetraeder fällt auf eine Fläche
mit grüner Farbe.
a) Untersuchen Sie, ob die Ereignisse paarweise unabhängig sind.
b) Schätzen Sie die Wahrscheinlichkeit für P(R∩B∩G). Überprüfen Sie Ihre Vermutung.
376
Aufgabe in modifizierter Form übernommen aus Kütting; Sauer; Padberg: Elementare Stochastik, S. 177.
117
Der frequentistische Wahrscheinlichkeitsbegriff II – Der Begriff der Unabhängigkeit
Aufgabe 3: Anwendung des frequentistischen Wahrscheinlichkeitsbegriffs
Überprüfen Sie Ihre intuitiven Vermutungen vom Arbeitsblatt („Sind Menschen gute Statistiker“).
a) Was halten Sie für wahrscheinlicher? Kreuzen Sie an!
○ (1) Mindestens 7 von 10 Neugeborenen in einem Krankenhaus sind Mädchen.
○ (2) Mindestens 70 von 100 Neugeborenen in einem Krankenhaus sind Mädchen.
○ (1) und (2) sind gleichwahrscheinlich.
b) Ist es als Roulette-Spieler sinnvoll sich die vorherigen Kugelziehungen anzuschauen?
Würden Sie einem Roulette-Spieler raten nach 10-maligen Rot im nächsten Versuch auf
Schwarz zu setzen? Ändert sich Ihr Ratschlag für das Spiel Black-Jack, falls mehrere Karten
bekannt sind?
c) Nehmen Sie Stellung zu folgenden (nicht ernst gemeinten) Aussagen:
-
Ein Flugreisender, der Angst vor Attentaten hat, sollte stets eine Bombe mit sich
führen. Die Wahrscheinlichkeit, dass gleichzeitig zwei Bomben an Bord sind, ist
fast Null!
-
Der Arzt eröffnet dem Patienten nach der Untersuchung: ,,Also, die Lage ist ernst.
Sie sind sehr krank; statistisch gesehen überleben 9 von 10 Menschen diese Krankheit nicht.“ Der Patient erbleicht. „Sie haben aber Glück“, beruhigt der Arzt. „Ich
hatte schon neun Patienten mit den gleichen Symptomen, und die sind alle tot.“
Vertiefung: Abituraufgabe (LK 2008, Nordrhein-Westfalen)
Der deutsche Basketballprofi Dirk Nowitzki spielt in der amerikanischen Profiliga NBA
beim Club Dallas Mavericks. In der Saison 2006/2007 erzielte er bei Freiwürfen eine Trefferquote von 90,4 %. Diskutieren Sie, in wie weit die Trefferquote Nowitzkis für jeden Wurf
gilt.
118
Der frequentistische Wahrscheinlichkeitsbegriff III – Wahrscheinlichkeitsverteilungen
Aufgabe 1: Das Galton-Brett & Das Bino-Ley377
Station 1: Das Bino-Ley
a) Schätzen Sie, wie ein Balkendiagramm aussehen könnte, wenn Sie in 20 Würfen jeweils
vier Münzen werfen und die Anzahl der Wappen zählen.
b) Führen Sie den Versuch anschließend durch und erstellen Sie ein Balkendiagramm. Tragen Sie danach Ihre Ergebnisse in Ihrer Gruppe (5 Personen) zusammen und erstellen
Sie ein gemeinsames Balkendiagramm. Vergleichen Sie das Balkendiagramm mit Ihrer
geschätzten Verteilung.
c) Verallgemeinern Sie die Situation, indem Sie die Münzwürfe in einem Baumdiagramm
darstellen.
Station 2: Das Galton-Brett
a) Schätzen Sie, wie das Galton-Brett aussehen könnte, wenn Sie 20 Kugeln durch den
Einlass am oberen Ende des Bretts hineinwerfen (Balkendiagramm).
b) Führen Sie den Versuch anschließend zuerst für 20 und dann für 100 Kugeln durch und
erstellen Sie jeweils ein Balkendiagramm. Vergleichen Sie das Balkendiagramm mit Ihrer geschätzten Verteilung.
c) Verallgemeinern Sie die Situation, indem Sie die einzelnen Ebenen des Galton-Bretts in
einem Baumdiagramm darstellen.
Zusammentragen der Stationsarbeit im Plenum
a) Vergleichen Sie die beiden Stationen miteinander. Welche Gemeinsamkeiten und Unterschiede können Sie feststellen?
b) Führen Sie eine Computersimulation durch und untersuchen Sie die Balkendiagramme.
Variieren Sie dabei zunächst die Anzahl der Versuche und anschließend die Wahrscheinlichkeit.
c) Untersuchen Sie nun die Mittelwerte und die Standardabweichung in den einzelnen Balkendiagrammen. Vergleichen Sie diese Ergebnisse, mit denen vom Arbeitsblatt „frequentistischer Wahrscheinlichkeitsbegriff I“ (vor allem Aufgabe 1 „Warum gibt es immer so wenige rote Gummibärchen in der Tüte?“)
377
Aufgabe in modifizierter Form übernommen aus Eichler; Vogel: Leitidee Daten und Zufall, S. 217, 223.
119
Der frequentistische Wahrscheinlichkeitsbegriff III – Wahrscheinlichkeitsverteilungen
Aufgabe 2: Diskrete Wahrscheinlichkeitsverteilungen
Ordnen Sie den Wahrscheinlichkeitsexperimenten der Aufgabe 1 ein kombinatorisches
Zählprinzip zu. Recherchieren Sie im Internet, ob aus den Urnenmodellen andere Verteilungen erschlossen werden können.
Aufgabe 3: Reflexion des frequentistischen Wahrscheinlichkeitsbegriffs
a) Nehmen Sie Stellung zu folgender Aussage:
„Wenn ich nur einen Versuch mache, dann interessiert mich nicht die Wahrscheinlichkeit,
ob der Versuch gelingt. Bei einem Versuch glückt dieser oder nicht. Die relative Häufigkeit,
mit der der Versuch bei einer sehr häufigen Versuchswiederholung gelingt, ist für einen
Versuch unerheblich.“
b) Ergänzen Sie auf dem Arbeitsblatt „Der Einstieg in die Stochastik“ die Tabelle in der
Zeile „frequentistischer Wahrscheinlichkeitsbegriff“.
120
Der subjektive Wahrscheinlichkeitsbegriff I – Die bedingte Wahrscheinlichkeit
Aufgabe 1: Riemer-Quader oder gewöhnlicher Würfel?378
Eine oder einer von Ihnen übernimmt die Spielleitung. Die Spielleitung wählt verdeckt den
Quaderwürfel oder den gewöhnlicher Spielwürfel aus und legt den anderen Würfel für den
Rest des Spiels zur Seite.
a) Schätzen Sie, mit welcher Wahrscheinlichkeit die Spielleitung den Quaderwürfel bzw.
den gewöhnlichen Spielwürfel für das Spiel ausgewählt hat.
b) Die Spielleitung würfelt mit dem ausgewählten Würfel einmal und nennt Ihnen die Augenzahl. Ändern sich Ihre vorab geschätzten Wahrscheinlichkeiten?
c) Die Spielleitung wirft nun ein zweites Mal, ein drittes Mal usw. den ausgewählten Würfel. Beurteilen Sie, ab wann Sie entscheiden können, ob die Spielleitung den Quaderwürfel oder den gewöhnlichen Spielwürfel ausgewählt hat.
Aufgabe 2: Die bedingte Wahrscheinlichkeit im Laplace- und im frequentistischen Modell379
Gruppe 1: Laplace-Modell
Zwei unterscheidbare Laplace-Spielwürfel werden einmal gleichzeitig geworfen. Der eine Würfel sei grün, der andere rot.
a) Berechnen Sie die Wahrscheinlichkeit, dass die Augensumme aus den Augenzahlen beider Spielwürfel größer als 9 ist?
b) Berechnen Sie die Wahrscheinlichkeit, dass die Augensumme aus den Augenzahlen größer als 9 ist, wenn man schon weiß, dass eine 6 gefallen ist?
c) Berechnen Sie die Wahrscheinlichkeit, dass die Augensumme größer als 9 ist, wenn man
schon weiß, dass der grüne Würfel eine Augenzahl kleiner als 6 zeigt?
d) Variieren Sie wie in Aufgabenteil b) und c) die Werte und verallgemeinern Sie, wie die
sogenannten bedingten Wahrscheinlichkeiten bestimmt können.
e) Diskutieren Sie den Zusammenhang zwischen den Pfadregeln, der bedingten Wahrscheinlichkeit und der Unabhängigkeit von Ereignissen.
378
379
Aufgabe in modifizierter Form übernommen aus Eichler; Vogel: Leitidee Daten und Zufall, S. 165.
Aufgabe in modifizierter Form übernommen aus Kütting; Sauer; Padberg: Elementare Stochastik, S. 170.
121
Der subjektive Wahrscheinlichkeitsbegriff I – Die bedingte Wahrscheinlichkeit
Gruppe 2: frequentistisches Modell
In der folgenden Tabelle sind die wegen Vergehen im Straßenverkehr im Jahre
2007 Verurteilte in der Bundesrepublik Deutschland festgehalten.
Jugendliche
Heranwachsende Erwachsene
Verurteilte mit Vergehen 5516
8832
80652
ohne Trunkenheit
Verurteilte mit Vergehen 1424
9394
106028
in Trunkenheit
6940
18226
186680
95000
116846
211846
a) Bestimmen Sie die relativen Häufigkeiten380 bezogen auf die Grundgesamtheit (211846).
b) Berechnen Sie den Anteil der verurteilten Erwachsenen wegen Vergehen im Straßenverkehr in Trunkenheit, falls man nur Erwachsene betrachtet.
c) Berechnen Sie den Anteil der Jugendlichen, falls nur Verurteilte mit Vergehen im Straßenverkehr ohne Trunkenheit betrachtet werden.
d) Variieren Sie wie in Aufgabenteil b) und c) die Werte und verallgemeinern Sie das Vorgehen, wie die sogenannten bedingten relativen Häufigkeiten beziehungsweise Wahrscheinlichkeiten bestimmt werden.
e) Diskutieren Sie den Zusammenhang zwischen den Pfadregeln, der bedingten Wahrscheinlichkeit und der Unabhängigkeit von Ereignissen.
380
Um Ihnen den Umgang mit den Daten zu erleichtern, betrachten Sie zunächst nur relative Häufigkeiten.
Diese dienen als zukünftige Schätzwerte für die Wahrscheinlichkeit.
122
Der subjektive Wahrscheinlichkeitsbegriff I – Die bedingte Wahrscheinlichkeit
Aufgabe 3: Wie sicher ist der AIDS-Test?381
Der sogenannte AIDS-Test ist einer der zuverlässigsten Tests, die jemals entwickelt
wurden. Er wird eingesetzt, um eine Infektion mit HIV festzustellen.382 Wegen der
hohen Gefahr der Verbreitung der tödlichen HIV-Infektion war sogar lange Zeit in der Diskussion, ob nicht die gesamte Bevölkerung zum AIDS-Test gezwungen werden soll. Der
AIDS-Test ist aber nicht perfekt. Wenn jemand HIV-infiziert ist, soll der Test positiv sein.
Zu 99,9% fällt er dann auch positiv aus. Andererseits wenn jemand nicht HIV-infiziert ist,
soll der Test natürlich negativ sein. Zu 99,7% fällt er dann tatsächlich negativ aus.
Angenommen, dass für alle Menschen in NRW ein AIDS-Test durchgeführt werden soll.
Laut Schätzung des Robert-Koch-Instituts sind bundesweit 0,05% der Bevölkerung HIVinfiziert, die Quote kann auch für NRW angenommen werden. Die Bevölkerungsstatistik
sagt, dass in NRW 18.000.000 Menschen leben.
a) Stellen Sie sich vor, eine beliebige Person aus NRW bekommt mitgeteilt, dass ihr Test
positiv ist. Schätzen Sie die Wahrscheinlichkeit, dass sie tatsächlich HIV-infiziert ist?
b) Gliedern Sie die getesteten Personen mit Hilfe einer Vierfeldertafel. Berechnen Sie jeweils die absoluten und die relativen Häufigkeiten.
c) Bestimmen Sie (mit Hilfe eines Baumdiagramms) gesuchte Wahrscheinlichkeit.
d) Bewerten Sie, ob sich alle Personen in NRW einem Aids-Test unterziehen sollten.
Der Satz von Bayes:
Bayes
Vertiefung: Riemer-Quader oder gewöhnlicher Würfel?
Berechnen Sie mit Hilfe des Satzes von Bayes, wie sich die Wahrscheinlichkeiten aus Aufgabe 1 ausgehend von Ihrer subjektiven Schätzung verändern.
381
Aufgabe in modifizierter Form übernommen aus Wassner; Biehler; Schweynoch: Authentisches Beurteilen,
S. 3.
382
Im Sprachgebrauch hat sich AIDS-Test eingebürgert. AIDS bezeichnet eigentlich die Krankheit, die man
bekommen kann, wenn man mit HIV infiziert ist. HIV kommt vom engl. „human immunodeficiency virus“ =
„Immunschwäche-Virus beim Menschen“.
123
Der subjektive Wahrscheinlichkeitsbegriff II – Die Basisrate
Aufgabe 1: Aus dem HIV/AIDS-Bericht II/2002, Robert-Koch-Institut Berlin383
HIV-Infektionen sind bei manchen Bevölkerungsgruppen deutlich häufiger als bei
anderen, man spricht von unterschiedlichen Basisraten. Z. B. bei homosexuellen
Männern, Drogenabhängigen, die ihren „Stoff“ intravenös spritzen, heterosexuellen Partnern von Abhängigen, außerdem Blutern oder Kindern HIV-infizierter Frauen (sog. Risikogruppen) sind die HIV-Basisraten viel höher als bei anderen Bevölkerungsgruppen. Nach
einer Schätzung aus dem Jahre 2002 gibt es in Berlin 7500 intravenös Drogenabhängige
(IVDA), davon sind 848 HIV-infiziert.
a) Berechnen Sie die Wahrscheinlichkeit für eine Person an Aids erkrankt zu sein, wenn
der Test384 positiv ausgefallen ist. Erklären Sie, warum dieser Wert viel höher als in
Aufgabe 3 des vorherigen Arbeitsblattes ist.
b) In einer Stadt mit 100.000 Einwohnern ist die Basisrate für eine HIV-Infektion nicht
bekannt. Es soll der Zusammenhang zwischen der Basisrate und der a-posteriori - Wahrscheinlichkeit einer HIV-Infektion, wenn der Test positiv war, untersucht werden. Zeichnen Sie mit Geograbra einen Funktionsgraph, der diese Wahrscheinlichkeit in Abhängigkeit von der Basisrate darstellt.
Aufgabe 2: Anwendung des subjektiven Wahrscheinlichkeitsbegriffs
Überprüfen Sie Ihre intuitiven Vermutungen vom Arbeitsblatt („Sind Menschen gute Statistiker“)
a) Das Taxiproblem
Ein Taxi war an einem nächtlichen Verkehrsunfall mit Fahrerflucht beteiligt. In der Stadt, in
der der Unfall passierte, gibt es zwei Taxiunternehmen, eines mit grünen und eines mit
blauen Taxis. Folgende Daten sind nun gegeben: (i) 85% aller Taxis in der Stadt sind blau,
die anderen 15% sind grün. (ii) Ein Zeuge identifizierte das davonfahrende Taxi als „grün“.
Das Gericht untersuchte nun die Fähigkeit des Zeugen, die Farbe eines Taxis bei Nacht richtig zu identifizieren. In der Versuchsreihe (die Hälfte der Taxis war blau, die andere Hälfte
war grün), konnte der Zeuge beide Farben zu 80% richtig identifizieren, aber zu 20% irrte
er. Berechnen Sie mit Hilfe des Satz von Bayes die Wahrscheinlichkeit.
383
Wassner; Biehler; Schweynoch: Authentisches Beurteilen, S. 9.
Die Sensitivität und die Spezifität des Aids-Tests sollen aus der Aufgabe 3 des vorherigen Arbeitsblattes
übernommen werden.
384
124
Der subjektive Wahrscheinlichkeitsbegriff II – Die Basisrate
b) Das Ziegenproblem
Sie nehmen an einer Spielshow im Fernsehen teil, bei der Sie eine von drei verschlossenen
Türen auswählen sollen. Hinter einer der Türen wartet der Preis, ein Auto, hinter den beiden
anderen stehen Ziegen. Sie zeigen auf eine Tür, sagen wir Nummer eins. Sie bleibt vorerst
geschlossen. Der Moderator weiß, hinter welcher Tür sich das Auto befindet; mit den Worten: ‚Ich zeige Dir mal was‘ öffnet er eine andere Tür, zum Beispiel Nummer drei, und eine
meckernde Ziege schaut ins Publikum. Er fragt: ‚Bleiben Sie bei Nummer eins, oder wählen
Sie Nummer zwei?“
c) Das Kästchenparadoxon Bertrands
Drei zweigeteilte Schubladen enthalten in jedem Teil eine Münze. Man kann sie nach rechts
oder nach links jeweils zur Hälfte herausziehen und sieht dann die eine Münze. Eine enthält
zwei Goldmünzen, eine zwei Silbermünzen und die letzte eine Silber- und eine Goldmünze.
Sie ziehen eine Schublade halb heraus und sehen eine Goldmünze. Berechnen Sie die Wahrscheinlichkeit, dass hinter dem zweiten Teil der Münze eine silberne Münze steckt.
d) Der Fall Sally Clark
Auf der Basis des DNA-Profils der am Tatort an der Leiche gefundenen Blutspur erstellte
der Sachverständige Dr. K. ein Gutachten, in dem er zu Protokoll gab, dass in einer Stadt
von der Größe Berlins ungefähr eine Million Männer als mögliche Täter in Frage kommen.
Im Falle der Schuld des Angeklagten zeigt die verwendete DNA-Analyse mit an Sicherheit
grenzender Wahrscheinlichkeit eine Übereinstimmung des DNA-Profils des Angeklagten
mit dem in der Blutprobe an der Leiche sichergestellten genetischen Fingerabdruck. Die
Wahrscheinlichkeit, dass der genetische Fingerabdruck eines Unschuldigen rein zufällig mit
dem DNA-Profil übereinstimmt, das in der Blutprobe an der Leiche gefunden wurde, beträgt
0,0001%. Im vorliegenden Fall stimmt das DNA-Profil der DNA-Probe des Angeklagten
mit dem DNA-Profil der am Tatort gefundenen Spur überein.
Stellen Sie sich vor, Sie sind Richter und müssen nun die Aussagekraft der gefundenen
DNA-Übereinstimmung bewerten: Mit welcher Wahrscheinlichkeit ist der Angeklagte tatsächlich Verursacher der am Tatort sichergestellten Spur? Mit welcher Wahrscheinlichkeit
ist er der Mörder?
125
Der subjektive Wahrscheinlichkeitsbegriff II – Die Basisrate
Aufgabe 3: Diskussion über die inhaltlichen Wahrscheinlichkeitsbegriffe zum Entscheiden von Hypothesen.
Betrachten Sie erneut die Aufgabe „Warum gibt es immer so wenige rote Gummibärchen in
der Tüte?“ auf dem Arbeitsblatt „Der frequentistische Wahrscheinlichkeitsbegriff I“. Erläutern Sie Ihr Vorgehen, um über Ihre Hypothese zu entscheiden. Vergleichen Sie dieses mit
der Vorgehensweise beim Entscheiden mit Hilfe des Satzes von Bayes. Wie wird beim Laplace-Modell über Hypothesen entschieden? Diskutieren Sie Chancen und Risiken der Vorgehensweisen.
Vertiefung: Chancen und Grenzen der Wahrscheinlichkeitsbegriffe
Werten Sie unsere bisherigen Erkenntnisse aus und vervollständigen Sie die Tabelle mit den
Chancen und Risiken der Wahrscheinlichkeitsbegriffe. Versuchen Sie zu erklären, was
Wahrscheinlichkeiten im mathematischen Sinne sind. Welche Fragen konnten mit keinem
der inhaltlichen Wahrscheinlichkeitsbegriffe beantwortet werden?
126
Der Axiomatische Wahrscheinlichkeitsbegriff I – Die Axiomatik nach Kolmogorov
Aufgabe 1: Die Axiomatik nach Kolmogorov
Bisher konnten wir die Wahrscheinlichkeiten nur berechnen, aber nicht
definieren, was Wahrscheinlichkeiten im mathematischen Sinne sind. Es
dauerte auch bis ins Jahr 1933 bis Kolmogorov diese Frage mit Hilfe eines
Axiomensystems klärte:
Kolmogorov
Definition: Axiomensystem Kolmogorovs im endlichen Fall
Ein Wahrscheinlichkeitsraum (Ω, P) ist ein Paar bestehend aus einer nichtleeren
Menge Ω={ω1 , … , ωn } und einer Funktion P: P(Ω)→ ℝ mit den Eigenschaften:
1) P(E) ≥ 0 für alle Teilmengen E von Ω (Nichtnegativität).
2) P(Ω) = 1 (Normiertheit).
3) P(E1 ∪ E2) = für alle Teilmengen E1, E2 mit E1∩E2 = Ø (Additivität).
Ω heißt Ergebnismenge, P(Ω) Ereignismenge, P Wahrscheinlichkeitsverteilung und
P(E) Wahrscheinlichkeit des Ereignisses E.
a) Vergleichen Sie das Axiomensystem Kolmogorovs mit den Eigenschaften des Laplacebzw. des frequentistischen Wahrscheinlichkeitsbegriffs. Welche Unterschiede und Gemeinsamkeiten gibt es?
Tipp: Sie haben bereits das Axiomensystem Hilberts in der Geometrie kennen gelernt.
b) Verallgemeinern Sie, was im mathematischen Sinne Wahrscheinlichkeiten sind.
127
Der Axiomatische Wahrscheinlichkeitsbegriff I – Die Axiomatik nach Kolmogorov
Aufgabe 2: Eigenschaften des Axiomensystems385
a) Beweisen Sie mit Hilfe des Axiomensystems folgende Eigenschaften einer Wahrscheinlichkeitsverteilung. Diese kennt Sie bereits aus den inhaltlichen Wahrscheinlichkeitsbegriffen.
- P(∅) = 0.
- P(E) ≤ 1 für alle E ⊆ Ω .
̅) = 1 − P(E) für alle E ⊆ Ω .
- P(E
- P(E1 ∪ E2) = P(E1) + P(E2) − P(E1∩E2) für alle E1, E2 ⊆ Ω .
- Speziell gilt: P(E) = ∑ω∈E P({ω}) und P(Ω) = ∑ω∈Ω P({ω})= ∑ni=1 P({ωi})= 1
b) Beweisen Sie mit Hilfe des Axiomensystems folgenden Satz:
Ist Ω = {ω1, ω2,…, ωn} eine endliche Ergebnismenge, so ist eine Wahrscheinlichkeitsverteilung P durch ihre Werte für die Elementarereignisse eindeutig festgelegt. Wird hierfür jedem
ωi ∈ Ω eine Zahl P({ωi}) ∈ [0; 1] zugeordnet, wobei ∑ni=1 P({ωi})= 1 gilt und
P(E)∶= ∑ω∈E P({ω}), so ist P eine Wahrscheinlichkeitsverteilung von P. Die Umkehrung
gilt ebenfalls.
3. Aufgabe: Erweiterung der Wahrscheinlichkeitsräume386
Erinnern Sie sich an „Aufgabe 1: Das Glücksrad“ des Arbeitsblattes „Der Laplace-Wahrscheinlichkeitsbegriff III“. Dort haben wir gesehen, dass wir keine Laplace-Wahrscheinlichkeiten ausrechnen können, falls der Ergebnisraum unendlich groß wird. Im Folgenden wollen wir dies verallgemeinern. Dazu unterscheiden wir abzählbar unendlich und überabzählbar unendlich große Wahrscheinlichkeitsräume. Wir betrachten wieder das gleiche Glücksrad.
385
386
Die Aufgabe wurde in modifizierter Form übernommen aus Büchter; Henn: Elementare Stochastik, S. 185.
Aufgabe in modifizierter Form übernommen aus Büchter; Henn: Elementare Stochastik, S. 188.
128
Der Axiomatische Wahrscheinlichkeitsbegriff I – Die Axiomatik nach Kolmogorov
Gruppe 1: Warten auf den Erfolg – Abzählbar unendliche Wahrscheinlichkeitsräume
Sie interessieren sich dafür, wie groß die Wahrscheinlichkeit dafür ist, dass Sie im 1., 2.
beziehungsweise n-ten Versuch gewinnen. Stellen Sie dafür zunächst die Ergebnismenge
auf und lösen Sie dann das Problem. Werten Sie aus, ob die Wahrscheinlichkeitsverteilung
noch über die Elementarereignisse definiert werden kann (Aufgabe 2b).
Tipp: Verwenden Sie zum Nachweis des dritten Axioms die geometrische Summenformel:
2
∑∞
i=1 P(ωi)=1 + q + q +… =
1
, wobei |q| <1 sein muss.
1−q
Zusatzinformation für zukünftige Mathematikstudent/innen: In überabzählbaren Mengen gilt der Satz aus Aufgabe 2b) nicht mehr in beide Richtungen. „Bei abzählbar unendlicher Ergebnismenge gilt jedoch nur die eine
Richtung. Zwar folgen die Kolmogorov-Axiome in der Formulierung von Aufgabe 2b aus der Festlegung auf
den Elementarereignissen, aber nicht umgekehrt! Der tiefere Grund ist, dass Axiom (III) nur die Additivität
von P für eine endliche Anzahl disjunkter Ereignisse fordert. Wir müssen also unser drittes Axiom durch fol∞
gendes ersetzen: Für abzählbar viele, disjunkte Teilmengen E i aus P(Ω) gilt: P(⋃∞
i=1 Ei)=∑i=1 P(Ei). Diese Ei-
genschaft nennt man σ-Additivität.
Gruppe 2: Überabzählbar unendliche Wahrscheinlichkeitsräume
a) Im obigen Glücksrad leuchtet eine rote Lampe auf, sobald der Zeiger des Glücksrades
die 6-Uhr Position überquert. Auf Nachfrage erklärt Ihnen der Standbesitzer, dass Sie
den Hauptgewinn bekommen, falls die Lampe leuchtet. Berechnen Sie die Wahrscheinlichkeit den Hauptgewinn zu erzielen. Werten Sie aus, ob die Wahrscheinlichkeitsverteilung noch über die Elementarereignisse definiert werden kann.
b) Berechnen Sie die Wahrscheinlichkeit, dass die Gleichung x 2+ax+b=0 mit a, b≤|1| eine
Lösung in ℝ besitzt. Testen Sie zunächst einige Kombinationen und verallgemeinern Sie
diese.
Vertiefung: Die bedingte Wahrscheinlichkeit in der Axiomatik Kolmogorovs
Beweisen Sie, dass durch PA: P(Ω)→ ℝ, B→ PA(B) ∶=P(B|A) eine neue Wahrscheinlichkeitsverteilung auf P(Ω) definiert wird.
129
Der Axiomatische Wahrscheinlichkeitsbegriff II – Zufallsvariablen & Erwartungswert/ Varianz
Aufgabe 1: Die Zufallsvariable387
Da wir uns durch die Axiomatik Kolmogorovs komplett vom Inhalt gelöst haben, benötigen
wir eine Funktion, die jedem Element der Ergebnismenge eine reelle Zahl zuweist. Solche
Funktionen heißen Zufallsvariablen und werden mit Großbuchstaben (meist Z) bezeichnet.
Definition: Zufallsvariable & Induzierte Wahrscheinlichkeitsverteilung
Ω sei eine diskrete Ergebnismenge. Dann ist eine Zufallsvariable Z eine reellwertige
Funktion auf Ω, d. h. Z: Ω →ℝ; ω→ Z(ω). Die vorgegebene Wahrscheinlichkeitsverteilung P wird jetzt auf die Zufallsvariable übertragen:
Es sei (Ω, P) ein diskreter Wahrscheinlichkeitsraum und Z eine Zufallsvariable auf Ω.
Dann wird durch PZ: P(Z(Ω))→ ℝ, A→ PZ(A) = P(Z-1(A)) eine Wahrscheinlichkeitsverteilung auf der Ereignismenge P(Z(Ω)) definiert, und (Z(Ω), PZ) ist ein Wahrscheinlichkeitsraum.
a) Geben Sie für folgende Beispiele eine Zufallsvariable an und erstellen Sie eine Wahrscheinlichkeitsverteilung (Tabelle und Balkendiagramm). Es wird jeweils mit zwei Laplace-Würfeln geworfen.
-
Die Augensumme
-
Die höchste der beiden Augenzahlen
-
Der Betrag der Differenz der Augenzahlen
b) Vergleichen Sie die beschreibende Statistik mit der Wahrscheinlichkeitsrechnung.
Tipp: Schauen Sie noch einmal Aufgabe 1c) des Arbeitsblattes „Wahrscheinlichkeitsverteilungen an“.
Definition: Erwartungswert und Varianz der Zufallsvariable
387
Aufgabe in modifizierter Form übernommen aus Lergenmüller: Mathematik Neue Wege, S. 108.
130
Der Axiomatische Wahrscheinlichkeitsbegriff II – Zufallsvariablen & Erwartungswert/ Varianz
Aufgabe 2: Chuck a Luck – Ein faires Spiel?388
Chuck a Luck ist ein einfaches Glücksspiel, bei dem Sie Ihren Einsatz (z. B. ein Euro) auf
eine Augenzahl seiner Wahl setzen. Anschließend wirft der Bankhalter mit 3 Würfeln. Je
nachdem wie viele Würfel die gesetzte Augenzahl anzeigen, bekommen Sie Ihren Einsatz
einfach, doppelt, oder dreifach zurück. Ansonsten haben Sie Ihren Einsatz verloren.
a) Diskutieren Sie, wann ein Spiel als fair gelten soll.
b) Führen Sie das Spiel ein paar Mal durch. Notieren Sie dabei jeweils Ihre durchschnittlichen Nettogewinn beziehungsweise -verlust.
c) Stellen Sie eine Zufallsvariable auf, die sich auf Ihre Gewinne bzw. Verluste bezieht und
berechnen Sie die Wahrscheinlichkeitsverteilung. Bestimmen Sie anschließend Erwartungswert und Zufallsvariable.
d) Simulieren Sie den durchschnittlichen Nettogewinn des Chuck a Luck.
Aufgabe 3: Rechenregel für den Erwartungswert und die Varianz389
a) Untersuchen Sie die Excel-Tabelle, indem Sie mit dem Schiebregler experimentieren
und finden Sie Antworten auf folgende Fragen:
-
Wie verändert sich der Erwartungswert E(Z) einer Zufallsvariable Z, wenn man zu
Z eine Konstante c addiert?
-
Was passiert mit dem Erwartungswert E(Z), wenn die Zufallsvariable Z mit einem
konstanten Faktor multipliziert wird?
-
Wie hängt der Erwartungswert von Y+Z von den Erwartungswerten Y und Z ab?
Auf ähnliche Art und Weise könnten Sie auf die Rechenregeln für die Varianz entdecken.
Diese lauten: V(a∙Z+c)=a∙V(Z) und falls Y und Z unabhängig sind: V(Y+Z)=V(Y)+V(Z).
Verifizieren Sie diese mit Hilfe der Excel-Tabelle.
b) Erläutern Sie die entdeckten Formeln, indem Sie zu jeder Formel ein Beispiel aus der
Glückspielwelt angeben.
c) Leiten Sie mit Hilfe der Rechenregeln den Erwartungswert und die Varianz der Binomialverteilung her.
388
389
Aufgabe in modifizierter Form übernommen aus Lergenmüller: Mathematik Neue Wege, S. 112.
Aufgabe in modifizierter Form übernommen aus Lergenmüller: Mathematik Neue Wege, S. 116.
131
Der Axiomatische Wahrscheinlichkeitsbegriff II – Zufallsvariablen & Erwartungswert/ Varianz
Vertiefung: Der Erwartungswert und die Binomialverteilung
a) Das St. Petersburg Paradoxon390
Ein Freund und Sie werfen eine Münze, und zwar so lange, bis zum ersten Mal oben Kopf
erscheint. Geschieht dies beim ersten Mal, so erhält Ihr Freund von Ihnen 2€. Kommt Kopf
erst beim 2. Mal, erhält er 4€, beim 3. Mal 8€ usw. Kommt Kopf also erst beim n-ten Wurf,
so erhält Ihr Freund 2n €. Was soll Ihr Freund einsetzen, damit dieses Spiel fair ist?
b) Berechnen Sie zu den Verteilungen B(20; 0,1; k), B(200; 0,1; k), B(20; 0,5; k) und B(20;
0,9; k) jeweils Erwartungswert und Varianz. Vergleichen Sie diese mit den Graphen aus
Aufgabe 1b) des Arbeitsblattes „Wahrscheinlichkeitsverteilungen“.391
c) Beurteilen Sie, ob folgende Aussagen richtig oder falsch sind:
390
391
-
Der Erwartungswert ist proportional zu der Versuchsanzahl n.
-
Die Varianz ist proportional zur Versuchszahl n.
-
Die Standardabweichung ist bei fester Versuchsanzahl am größten, wenn p=0,5.
Aufgabe in modifizierter Form übernommen aus Büchter; Henn: Elementare Stochastik, S. 288.
Aufgabe in modifizierter Form übernommen aus Lergenmüller: Mathematik Neue Wege, S. 126.
132
Der axiomatische Wahrscheinlichkeitsbegriff III – Das schwache Gesetz der großen Zahlen
Aufgabe 1: Das schwache Gesetz der großen Zahlen
Erinnern Sie sich an Jakobs Bernoullis Zitat aus der Vertiefung des Arbeitsblattes „frequentistischer Wahrscheinlichkeitsbegriff I“. Dieser fragte sich, wie die relativen Häufigkeiten
und die Wahrscheinlichkeit zusammenhängen. Diese Frage kann nun mit Hilfe des axiomatischen Wahrscheinlichkeitsbegriffs beantwortet werden. Die Beweisstruktur wurde bereits
von Jakob Bernoulli entdeckt, sodass das schwache Gesetz der großen Zahlen auch als das
Bernoulli’sche Gesetz der großen Zahlen bezeichnet wird.
a) Ordnen Sie die einzelnen Sätze des Beweises:
Diese Kenndaten ersetzte Bernoulli nun in der Ungleichung von Tschebycheff, sodass er
P(|Z - p| ≤ ɛ) > 1 -
p·(1−p)
n·ɛ²
erhält.
Sei (Ω,P) ein diskreter Wahrscheinlichkeitsraum und Z eine Zufallsvariable auf Ω mit dem
Erwartungswert μ und der Standardabweichung σ. Dann gilt: P(|Z - μ| ≤ ɛ) > 1 -
σ²
ɛ²
.
Durch die Allgemeingültigkeit der Tschebycheff-Ungleichung konnte sich Bernoulli auf
eine B(n,p)-verteilte Zufallsvariable Z beschränken.
1
Bernoulli definierte sich eine neue Zufallsvariable Z‘:= n ·Z, um die relative Häufigkeit beschreiben zu können.
1
Den größten Wert, den der Zähler p·(1-p) annehmen kann, liegt bei 4.
Voraussetzung für das Bernoulli‘sche Gesetz der großen Zahlen ist die Ungleichung von
Tschebycheff392 für Zufallsvariablen:
392
Eine analoge Ungleichung gibt es auch für die beschreibende Statistik. Dort liefert sie eine Abschätzung für
die relative Häufigkeit der Werte, die in ein vorgegebenes Intervall um das arithmetische Mittel fallen. Die
Entsprechungen von Merkmal und Zufallsvariable liefern direkt die Tschebycheff-Ungleichung für Zufallsvariablen.
133
Der axiomatische Wahrscheinlichkeitsbegriff III – Das schwache Gesetz der großen Zahlen
Sei (Ω, P) ein endlicher Wahrscheinlichkeitsraum und E ⊆ Ω ein Ereignis mit der Wahrscheinlichkeit P(E) =p. Die Zufallsvariable Z´ beschreibe die relative Häufigkeit des Eintre1
tens von E bei n unabhängigen Versuchen. Dann gilt: P(|Z‘ - p| ≤ ɛ) > 1 - 4·n·ɛ² und
lim P(|Z′ − p| ≤ ɛ)=1.
n→∞
Durch die Eigenschaften des Erwartungswert und der Varianz erhält er auch für diese Zufallsvariable die entsprechenden Kenndaten: E(Z‘)=p und V(Z‘) =
p·(1−p)
n
.
Hieraus folgt das Bernoulli´sche Gesetz der großen Zahlen:
Die Ungleichung von Tschebycheff gibt an, mit welcher Wahrscheinlichkeit die Werte einer
Zufallsvariable in ein vorgegebenes Intervall um den Erwartungswert fallen.
Den Erwartungswert E(Z) = n·p und die Varianz V(Z) = n·p·(1-p) sind ihm schon bekannt.
b) Berechnen Sie, wie oft wir würfeln müssten um die Wahrscheinlichkeit mit ε = 1% mit
einer Sicherheit von 99% zu schätzen.
c) Vergleichen Sie das empirische Gesetz der großen Zahlen mit dem schwachen Gesetz
der großen Zahlen.
134
Der axiomatische Wahrscheinlichkeitsbegriff III – Das schwache Gesetz der großen Zahlen
Aufgabe 2: Prognoseintervalle393
1
Wir betrachten einen Laplace-Münzwurf, das heißt Z sei durch Binomialverteilung mit p=2
modelliert.
a) Berechnen Sie die Wahrscheinlichkeit, dass die Trefferanzahl von Z (Wappen) vom Erwartungswert μ um nicht mehr als die Standardabweichung σ in Abhängigkeit von n
abweicht.394 Bestimmen Sie die Werte für n = 50, n = 100 und n = 200 von Hand und
stellen Sie eine Vermutung auf. Bestätigen Sie diese mit Ihrem Grafikfähigen Taschenrechner.
b) Überprüfen Sie Ihre gemachten Beobachtungen auch für 2σ und 3σ.
Für zahlreiche Anwendungen ist es von Interesse, in welchem zum Erwartungswert symmetrische Intervall die Trefferwahrscheinlichkeit X mit einer bestimmten Wahrscheinlichkeit fällt. Für eine 95%-Sicherheit, dass P(|X - μ| ≤ a) ist, nimmt man a = 1,96 ∙ σ an. Wir
bezeichnen daher das Intervall [μ - 1,96 ∙ σ; μ + 1,96 ∙ σ] als das 95%-Prognoseintervall.
c) Bestimmen Sie das 95%-Prognoseintervall für die absolute Anzahl und die relative Häufigkeit der Treffer jeweils für die drei Wurfserien (n = 50, n = 100 und n = 200).
d) Begründen Sie, dass das 95%-Prognoseintervall für die relativen Häufigkeiten proportional zu
1
√n
kleiner wird.
Aufgabe 3: Abschlussdiskussion der Wahrscheinlichkeitsbegriffe
Vor Ihnen liegen Karten mit einer gewissen Person (Laplace, von Mises, Bayes, Kolmogorov) drauf, die jeweils für einen gewissen Wahrscheinlichkeitsbegriff stehen. Versammeln
Sie sich in den Gruppen, die die gleiche Person bekommen haben. Reflektieren Sie die
Wahrscheinlichkeitsmodelle (Ihre Tabelle kann Ihnen dabei helfen). Bereiten Sie sich auf
eine Fishbowl-Diskussion vor, bei der Sie Ihr Wahrscheinlichkeitsmodell verteidigt und versucht die anderen Modelle anzugreifen.
Laplace
393
394
Von Mises
Bayes
Kolmogorov
Aufgabe in modifizierter Form übernommen aus Lergenmüller: Mathematik Neue Wege, S. 128, 132.
Dies bedeutet: P(|X-μ|≤σ)
135
Die Stochastische Modellbildung
Aufgabe 1: Der Modellierungskreislauf395
a) Beschreiben Sie den Modellierungskreislauf.
b) Übertragen Sie den Modellierungskreislauf auf Aufgabe 1 des Arbeitsblattes „Einstieg
in die Stochastik“.
c) Beurteilen Sie, welcher Punkt des Modellierungskreislaufes Ihnen am wichtigsten erscheint.
Aufgabe 2: Das Paradoxon von Bertrand396
Vorgegeben sei ein Kreis mit dem Radius r. Wie groß ist die Wahrscheinlichkeit, dass eine willkürlich (zufällig) in diesem Kreis gezogene Sehne
länger als die Seite des dem Kreis einbeschriebenen gleichseitigen Dreiecks397 ist?
Gruppe 1: Wahl eines Punktes im Inneren des Kreises, der Mittelpunkt der Sehne ist.
Gruppe 2: Wahl eines Punktes auf dem Kreis, der Eckpunkt eines gleichseitigen Dreiecks
ist.
Gruppe 3: Wahl eines Punktes auf einem festen Durchmesser des Kreises.
a) Berechnen Sie jeweils in Ihrer Gruppe die Wahrscheinlichkeit.
b) Diskutieren Sie, welche Gruppe die richtige Lösung gefunden hat.
395
396
Aufgabe in modifizierter Form übernommen aus Büchter; Henn: Elementare Stochastik, S. 199.
Aufgabe in modifizierter Form übernommen aus Kütting; Sauer; Padberg: Elementare Stochastik, S. 123.
397
Im gleichseitigen Dreieck mit Seitenlänge a sind die drei Höhen zugleich Winkelhalbierende und Seiten̅̅̅̅̅=𝑟 .
halbierende. Sie schneiden sich im Punkt M. Einfache Rechnungen zeigen, dass gilt: a=r∙√3 und 𝑀𝐷
2
136
Die Stochastische Modellbildung
Aufgabe 3: Abituraufgabe (GK 2010, Hessen)
a) Werten Sie aus, mit welchem Wahrscheinlichkeitsbegriff gearbeitet werden soll.
b) Berechnen Sie die Abituraufgaben.
c) Beurteilen Sie die Musterlösungen im Hinblick auf die Modellierung der Wahrscheinlichkeitsbegriffe (folgende Seite).
137
Die Stochastische Modellbildung
138
6.2 Tabelle – Möglichkeiten und Grenzen der Wahrscheinlichkeitsbegriffe
Wahrscheinlichkeitsbegriffe
Laplace-Wahrscheinlichkeitsmodell
Bestimmung
der
Wahrscheinlichkeit a
priori durch theoretische
Überlegungen (ZählverGünstige
fahren):
Mögliche
Möglichkeiten
Grenzen
Offene Fragen
Effektiv in der Glückspielwelt.
Keine Versuchsdurchführung notwendig  schnelle, theoretische a
priori Bestimmung möglich (Hilfsmittel aus der Kombinatorik).
Abzählen spiegelt natürliches Häufigkeitsformat wider.
Mengenbetrachtung ähnlich zum axiomatischen Modell.
Ähnliche Vorgehensweise beim geometrischen Wahrscheinlichkeitsbegriff (Dichtefunktion wird vorbereitet)
Scheinbare absolute Gewissheit
Außerhalb der Glücksspielwelt nicht
überzeugend.
Keine Möglichkeit, falls die Gleichwahrscheinlichkeit der Ereignisse (Prinzip
des unzureichenden Grundes) nicht gegeben ist.
Betrachtung des Flächenverhältnisses
nicht immer möglich (Quaderwürfel)
Niemals beweisbar (frequentistische Betrachtungen notwendig).
Keine Alternative sinnvoll  hypothetischer Charakter geht verloren.
Nur für endliche Versuchsreihen anwendbar.
Definition der Wahrscheinlichkeit nicht
möglich (Zirkelschluss).
Scheinbare absolute Gewissheit.
Wie kann ich in kontinuierlichen Wahrscheinlichkeitsräumen
Wahrscheinlichkeiten
berechnen?
Wie kann ich Wahrscheinlichkeit definieren?
139
Frequentistisches
Wahrscheinlichkeitsmodell
Bestimmung von Wahrscheinlichkeiten
a
posteriori auf Grundlage
des empirischen Gesetzes der großen Zahlen
Bestimmung der Wahrscheinlichkeit
im Nachhinein (a posteriori).
Simulation als Hilfsmittel.
Theoretisch unendlich oft wiederholbare Zufallsexperimente (breiter angelegt als das Lapalce-Modell).
Verbindung zur Statistik und zu Häufigkeitsverteilungen (Umsetzung des
Bruner’schen Spiralprinzip).
Einbezug von Daten für den Alltag
sehr wichtig.
Auflösung des deterministischen Bildes der StochastikUnsicherheit wir
deutlich (Charakter des Zufalls).
Subjektives
Wahr- Prinzipiell alles möglich, so lange die
Eigenschaften einer Wahrscheinlichscheinlichkeitsmodell
keit beachtet werden.
Intuition als Ausgangs- Aufgreifen der Intuition möglich und
punkt und Lernen aus Lernen aus Erfahrung (AlltagsbedeuErfahrung bzw. Daten
tung).
Stabilisation der subjektiven Ausgangslage mit Hilfe des Satzes von
Bayes bzw. dem empirischen Gesetz
der großen Zahlen.
Auflösung des deterministischen Bildes der Mathematik.
Bestimmung der Wahrscheinlichkeit erst
a posteriori (oft sehr lange Versuchsreihen notwendig).
Unabhängigkeit der einzelnen Zufallsexperimente notwendig.
Theoretisch unendlich oft wiederholbare
Zufallsexperimente Einmalige Versuche nicht modellierbar.
Unklarheiten wie Stabilisation und genügend oft beim empirischen Gesetz der
großen Zahlen (unliebsame Schwankung
auch nach vielen Versuchen).
Schwierigkeiten des empirischen Gesetzes der großen Zahlen ebenfalls bei der
Stabilisation des Häufigkeitsverteilungen und des Erwartungswertes zu findenNur möglichst gute Schätzungen,
die stets subjektiv sind.
Keine unendlichen Mengen.
Definition von Wahrscheinlichkeit nicht
möglich.
Subjektives Urteil wird mit einbezogen
(Abhängigkeit vom Wissensstand einer
Person).
Oft intuitive Fehleinschätzungen bei bedingten Wahrscheinlichkeiten (z. B. Basisrate).
Stabilisation der subjektiven Ausgangslage mit Hilfe des Satzes von Bayes bzw.
dem empirischen Gesetz der großen Zahlen.
In welchem Verhältnis stehen
relative Häufigkeiten und
Wahrscheinlichkeit?
Wie kann ich Wahrscheinlichkeit definieren?
Wie kann ich dies mathematisch darstellen?
Wie kann ich Wahrscheinlichkeit definieren?
140
Neue Interpretation des Ergebnisses immer notwendig (keine Bestätigung einer
Hypothese).
Keine Definition von Wahrscheinlichkeit möglich.
Axiomatisches Wahr- Loslösung vom Inhalt.
Definition der Wahrscheinlichkeit als
scheinlichkeitsmodell
normiertes Maß.
Aufgabe des Inhalts und Eigenschaften der inhaltlichen WahrAufstellen eines Bezie- scheinlichkeitsbegriffe als
hungssystems auf Basis Ausgangspunkt.
einer Mengenalgebra
Starke Verbindung zur beschreibenden Statistik.
Betrachtung kontinuierlicher Mengen
möglich.
Verbindung relative Häufigkeit und
Wahrscheinlichkeit wird durch das
schwache Gesetz der großen Zahlen
geklärt
Unsicherheit wird verborgen.
Loslösung vom Inhalt.
Mathematik und nicht die Schüler bzw.
der Alltag im Zentrum.
Modellierung der Situation mit Hilfe der
inhaltlichen
Wahrscheinlichkeitsbegriffe dennoch notwendig.
Unsicherheit wird verborgen.
141
6.3 Lösungen zu Beweisen
Eigenschaften der Laplace-Wahrscheinlichkeiten398
Da |∅| = 0 und 0 ≤ |E| ≤ |Ω| = n, gilt a) und b).
̅|.
c) Gilt wegen |Ω| = |E| + |E
d) Da E1∩E2 = ∅ gilt, ist |E1 ∪ E2| = |E1| + |E2|.
e) In der Summe |E1| + |E2| sind die Elemente von E1∩E2 zweimal gezählt worden. Also gilt
|E1∪E2| = |E1| + |E2| − |E1∩E2|, woraus die Formel folgt.
f) Dies ist klar, da bei einem Laplace-Experiment P({ω}) =
Eigenschaften des Axiomensystems
|{ω}|
|Ω|
1
= |Ω|.
399
a) 1= P(Ω) = P(Ω∪∅) = P(Ω) + P(∅) = 1 + P(∅), woraus P(∅) = 0 folgt.
̅) = P(E) + P(E
̅) ≥ P(E), woraus P(E) ≤ 1 und P(E
̅) = 1 − P(E)
b) und c) 1 = P(Ω) = P(E∪E
folgen.
d) P(E1∪E2) = P(E1\ E2 ∪ (E1∩E2) ∪ E2\ E1) = P(E1\ E2) + P(E1∩E2) + P(E2\ E1) = P(E1\ E2)
+ P(E1∩E2) + P(E2\ E1) + P(E1∩E2) − P(E1∩E2) = P(E1) + P(E2) − P(E1∩E2).
e) folgt durch wiederholte Anwendung des Axioms III.
Festlegung von Wahrscheinlichkeitsverteilungen400
Axiom I gilt, da alle P({ω}) ≥ 0 sind. Axiom II gilt wegen der Gleichung P(Ω)=∑ni=1 P({ωi)}
= 1. Es seien nun E1={ω1,…, ωa} und E2 = {ωa+1,…, ωb} mit E1∩E2=∅. Dann gilt:
P(E1∩E2) = ∑bi=1 P({ωi)} = ∑ai=1 P({ωi)} + ∑bi=a+1 P({ωi)} = P(E1) + P(E2), also Axiom 3.
Die Umkehrung gilt wegen des Axiomensystems Kolmogorovs.
Die Wahrscheinlichkeitsverteilung der bedingten Wahrscheinlichkeit401
Es ist zu zeigen, dass die Axiome Kolmogorovs gelten:
I: PA(B) = P(B|A) =
P(A∩B)
II: PA(Ω) = P(Ω|A) =
P(A)
≥ 0 für alle E ∈ P(Ω), da P(A ∩ B) ≥ 0 und P(A) > 0.
P(A ∩ Ω)
P(A)
= 1,
III: Es seien B, C ∈ P(Ω) mit B∩C = ∅. Dann gilt PA(B∪C) = P(B∪C |A) =
P((A ∩ B) ∪ (A ∩ C))
=
P(A)
=
P(A ∩ B) + P(A ∩ C)
P(A)
=
P(A ∩ B)
P(A)
+
P(A ∩ C)
P(A)
P(A ∩ (B ∪ C))
P(A)
= PA(B) + PB(C).
398
Büchter; Henn: Elementare Stochastik, S. 520.
Ebd., S. 185.
400
Ebd., S. 522.
401
Ebd., S. 522.
399
142
6.4 Verwendete Abbildungen auf den Arbeitsblättern
Aids-Schlaufe. In: Weltaidstag. URL: http://www.welt-aids-tag.de/fileadmin/user_upload/schleifen/images/WAT_Schleife_ohne-Text_1200x1200px_w.jpg
(Abgerufen: 08.06.2016, 13:00).
Baumdiagramm. Quelle: Eigene Konzeption
Bayes. In: Büchter; Henn: Elementare Stochastik, S. 221.
Bernoulli-Briefmarke. In: Büchter; Henn: Elementare Stochastik, S. 346.
Blaues und grünes Taxi. Quelle: Eigene Konzeption.
Chevalier de Méré. In: Büchter; Henn: Elementare Stochastik, S. 267.
Euro-Münze.
In:
Europa
Infoshop.
URL:
http://www.europa-infoshop.de/Euro-
Info/euro_muenzen_scheine/euro_muenzen_Deutschland/img_2008/1euro.jpg (Abgerufen:
08.06.20-16, 12:44 UTC).
Fermat. In: Büchter; Henn: Elementare Stochastik, S. 265.
Fußball-Toto-Spielschein. In: Büchter; Henn: Elementare Stochastik, S. 231.
Galton-Brett und Bino-Ley. In: Eichler; Vogel: Leitidee Daten und Zufall, S. 223.
Glücksrad. In: Vogt, Thomas: Powerpoint Präsentation (Vorbesprechung 01.02.2016).
Gummibärchen.
In:
Youngstarswiki.
URL:
https://www.youngstarswiki.org/uplo-
ads/tx_tdcwiki/589411_original_R_by_guenther%20gumhold_pixelio.de.jpg (Abgerufen:
08.06.2016, 12:42 UTC).
Kolmogorov. In: Büchter; Henn: Elementare Stochastik, S. 183.
Laplace. In: Büchter; Henn: Elementare Stochastik, S. 167.
Lotto-Spielschein. In: Büchter; Henn: Elementare Stochastik, S. 233.
Modellierungskreislauf. In: Büchter; Henn: Elementare Stochastik, S. 199.
Pascal. In: Büchter; Henn: Elementare Stochastik, S. 265.
Rennquintett-Spielschein. In: Büchter; Henn: Elementare Stochastik, S. 232.
Riemer-Würfel und Normaler Würfel. In: Eichler; Vogel: Leitidee Daten und Zufall, S. 147.
143
Roter und grüner Würfel. In: Static Zonar. URL: http://static.zoonar.de/img/www_repository4/7e/ab/3d/10_4ef272395823c24932f80968a0958e43.jpg
(Abgerufen:
08.06.2016,
12:58 UTC).
Sehnenparadoxon von Bertrand. In: Kütting; Sauer; Padberg: Elementare Stochastik, S. 124.
Spielfeld Siedler von Catan. In: Brettspiel Report. URL: http://www.brettspiele-report.de/images/die_siedler_von_catan/staedte_und_ritter/die_siedler_von_catan_staedte_und_ritter_beispiel_12.jpg (Abgerufen: 08.06.2016, 11:55 UTC).
Stop-Schild. In: Static Woxikon. URL: http://static.woxikon.com/images/verkehrszeichen/halt_vorfahrt.gif (Abgerufen: 08.06.2015, 12:59 UTC).
Von Mises. In: Büchter; Henn: Elementare Stochastik, S. 175.
Würfel. In: Nimrods. URL: http://www.nimrods.de/Knobel1.gif (Abgerufen: 08.06.2016,
12:46 UTC).
Ziegenproblem. In: Procommerz. URL: http://www.procommerz.de/wissen/ziegenproblem/img/drei_tore_3.png (Abgerufen: 08.06.2016, 11:24 UTC).
144
6.5 Lehrplan Mathematik
145
146
147
7. Quellen und Literaturverzeichnis
Althoff, Heinz: Wieviel Kombinatorik benötigt man in einem Grundkurs Stochastik? In:
MU. Der Mathematikunterricht 1 (1984), S. 94 – 99.
Abituraufgaben Hessen. In: Abiturloesung. URL: http://www.abiturloesung.de/al_upload/Hessen/Gymnasium/pdf/2010_GK_Stochastik_Aufgabe_C1.pdf
(Abgerufen: 03.06.2016, 15:10 UTC).
Barth, Friedrich; Haller, Rudolf: Stochastik Leistungskurs. München 1998.
Barth, Friedrich; Haller, Rudolph: Soll ich das Spiel wagen? Sinn und Unsinn des Erwartungswerts am Beispiel des Petersburger Problems. In: Stochastik in der Schule 1 (2010), S.
19-27.
Bartz, Stefan: Denkfallen vermeiden (2)–Am Beispiel des Geschwisterproblems. In:
Stochastik in der Schule 2 (2011), S. 30-33.
Basler, Herbert: Grundbegriffe der Wahrscheinlichkeitsrechnung und statistischen Methodenlehre: mit 34 Aufgaben und Lösungen. Heidelberg 1994 (Physica-Lehrbuch).
Bea, Wolfgang: Stochastisches Denken. Analysen aus kognitionspsychologischer und didaktischer Perspektive. Frankfurt 1995 (Psychologie des Entscheidungsverhaltens und des
Konfliktes, Bd. 6).
Beck-Bornholdt, Hans-Peter; Dubben, Hans-Hermann: Der Schein der Weisen. Irrtümer und
Fehlurteile im täglichen Denken. Reinbek bei Hamburg 2003.
Bender, Peter: Grundvorstellungen und Grundverständnisse für den Stochastikunterricht. In:
Stochastik in der Schule 1 (1997), S. 8-33.
Bentz, Hans-Joachim: Empirische Untersuchungen zum Wahrscheinlichkeitsbegriff. In:
Praxis der Mathematik in der Schule 33 (1991), S. 1-6.
Biehler, Rolf: Computers in Probability Education. In: Kapadia, Ramesh: Chance encounters: probability in education. Dordrecht 1991, S. 169-212.
Biehler, Rolf: Denken in Verteilungen-Vergleichen von Verteilungen. In: MU. Der Mathematikunterricht 3 (2007), S. 3-11.
Biehler, Rolf: Die Gesetze der großen Zahlen als heuristische Hilfsmittel zur Begriffsbildung
in der Stochastik. In: Sproesser, Ute; Wessolowski, Silvia; Wörn, Claudia: Daten, Zufall und
der Rest der Welt. Wiesbaden 2014, S. 13-26.
148
Biehler, Rolf: Statistische Kompetenz von Schülerinnen und Schülern - Konzepte und 97
Ergebnisse empirischer Studien am Beispiel des Vergleichs von statistischen Verteilungen.
In: Borovcnik, Manfred; Engel, Joachim; Wickmann, Dieter (Hg.): Anregungen zum
Stochastikunterricht. Hildesheim 2001, S. 97-114.
Biehler, Rolf; Engel, Joachim: Stochastik. Leitidee Daten und Zufall. In: Bruder, Regina;
Hefendehl-Hebeker, Lisa; Schmidt-Thieme, Barbara; Weigand, Hans-Georg: Handbuch der
Mathematikdidaktik. Berlin, Heidelberg 2015.
Biehler, Rolf; Maxara, Carmen: Integration von stochastischer Simulation in den Stochastikunterricht mit Hilfe von Werkzeugsoftware. In: MU. Der Mathematikunterricht 3 (2007),
S. 45-61.
Birnbaum, Ian: Die Interpretation statistischer Signifikanz. In: Stochastik in der Schule 2
(1982), S. 42-45.
Boor, Boris (Hg.): Lambacher Schweizer. Mathematik für Gymnasien. Stuttgart 2003.
Borovcnik, Mafred; Bentz, Hans-Jürgen; Kapadia, Ramesh: A Probabilistic Perspektiv. In:
Kapadia, Ramesh: Chance encounters: Probability in education. Dordrecht 1991, S. 169212.
Borovcnik, Manfred: Stochastik im Wechselspiel von Intuitionen und Mathematik. Mannheim 1992 (Lehrbücher und Monographien zur Didaktik der Mathematik, Bd. 10).
Borovcnik, Manfred: Ein intuitiver Zugang zur bedingten Wahrscheinlichkeit und zur
Bayes-Formel. In: Stochastik in der Schule 3 (1990), S. 22-35.
Borovcnik, Manfred: Stochastik im Wechselspiel von Intuitionen und Mathematik. Mannheim 1992 (Lehrbücher und Monographien zur Didaktik der Mathematik, Bd. 10).
Borovcnik, Manfred: Zum Anwendungsproblem in der Statistik. In: Mathematica didactica
1 (1984), S. 21-35.
Bosch, Karl: Elementare Einführung in die Wahrscheinlichkeitsrechnung. Wiesbaden 2011.
Brunner, Esther: Ein Prozessmodell des schulischen Beweisens. In: Roth, Jürgen; Ames,
Judith (Hg.): Beiträge zum Mathematikunterricht. Koblenz 2014, S. 269-272.
Büchter, Andreas & Henn, Hans-Wolfgang: Was heißt eigentlich "zufällig"? Das Bertrand'sche "Sehnen-Paradoxon" als Ausgangspunkt für stochastische Begriffsbildung. In:
Mathematica didactica 1 2005, S. 122-141.
149
Büchter, Andreas: (Lebens-)Gefährliche Trugschlüsse. Fehler vermeiden beim Denken in
Wahrscheinlichkeiten. In: Eikenbusch, Gerhard; Leuders, Timo (Hg.): Lehrer-Kursbuch Statistik. Berlin 2004, S. 127-134.
Büchter, Andreas: Daten und Zufall entdecken. Aspekte eines zeitgemäßen Stochastikunterrichts. In: Mathematik lehren. Erfolgreich unterrichten. Konzepte und Materialien 138
(2006), S. 4-11.
Büchter, Andreas; Henn, Hans-Wolfgang: Elementare Stochastik. Eine Einführung in die
Mathematik der Daten und des Zufalls. Berlin 2007 (Mathematik für das Lehramt).
Büchter, Andreas; Henn, Hans-Wolfgang: Stochastische Modellbildung aus unterschiedlichen Perspektiven. Von der Genueser Lotterie über Urnenaufgaben zur Keno Lotterie. In:
Stochastik in der Schule 3 (2004), S. 28-41.
Büchter; Andreas; Hußmann, Stephan; Leuders, Timo; Prediger, Schüleranne: Den Zufall
im Griff? Stochastische Vorstellungen fördern. In: Praxis der Mathematik in der Schule 4
(2005), S. 1-7.
Buth, Manfred: Methodische Anregungen zur Behandlung der bedingten Wahrscheinlichkeit. In : Mathematischer und Naturwissenschaftlicher Unterricht 7 (2003), S. 391-394.
Cosmides, Leda; Tooby, John: Are Humans Good Intuitive Statisticians after all? Rethinking
Some Conclusions from the Literature on Judgment Under Uncertainty. In: Cognition 58
(1996), 1-73.
Dabrock, Heinz: Zur Erarbeitung des empirischen Gesetzes der großen Zahlen im Stochastikunterricht. In: Stochastik im Schulunterricht 3 (1990), S. 36-47.
Dahl, Henrik: Unabhängigkeit Unterrichten. In: Stochastik in der Schule 3 (1998), S. 43-49.
Devlin, Keith: Pascal, Fermat und die Berechnung des Glücks: Eine Reise in die Geschichte
der Mathematik. München 2009.
Diepgen, Raphael: Ein Witz! Kritik und Gegenkritik zur Nowitzki-Aufgabe im NRW Zentralabitur. In: Stochastik in der Schule 2 (2010), S. 23-26.
Diepgen, Raphael: Was Schüler zum Hypothesentesten wissen sollten. In: Stochastik in der
Schule 1 (1985), S. 32-36.
Dinges, Hermann: Zum Wahrscheinlichkeitsbegriff für die Schule. In: Stochastik im Schulunterricht. Beiträge zum 3. Internationalen Symposium für Didaktik der Mathematik vom
29.9. bis 3.10.1980. Wien 1981, S. 49-63.
150
Dreher, Anika: Baumdiagramme und der Rest der Welt. In: Sproesser, Ute; Wessolowski,
Silvia; Wörn, Claudia: Daten, Zufall und der Rest der Welt. Wiesbaden 2014, S. 55-70.
Eichelsbacher, Peter: Mit RUNS den Zufall besser verstehen. In: Stochastik in der Schule
01 (2002), S. 2-8.
Eichler, Andreas: Vorstellungen von Lehrerinnen und Lehrern zum Stochastikunterricht. In:
MU. Der Mathematikunterricht 4/5 (2002), S. 26-44.
Eichler, Andreas: Was ist Wahrscheinlichkeit? Individuelle Unterrichtskonzepte von Lehrerinnen und Lehrern. In: MU. Der Mathematikunterricht 3 (2003), S. 69-82.
Eichler, Andreas; Vogel, Markus: Leitfaden Stochastik. Für Studierende und Ausübende des
Lehramts. Wiesbaden 2011.
Eichler, Andreas; Vogel, Markus: Leitidee Daten und Zufall. Von konkreten Beispielen zur
Didaktik der Stochastik. Wiesbaden 2013.
Engel, Arthur: Der Stochastische Abakus. In: Stochastik in der Schule 2 (2006), S. 28-37.
Engel, Arthur: Stochastik. Stuttgart 1992 (Klett Studienbücher: Mathematik).
Engel, Arthur: Wahrscheinlichkeitsrechnung und Statistik. Bd. 1. Stuttgart 1973.
Engel, Joachim: Entdecken von Wahrscheinlichkeitsverteilungen: wie lassen sich Muster
und Strukturen in empirischen Daten erkennen? In: MU. Der Mathematikunterricht (2) 1999,
S. 4 - 30.
Engel, Joachim; Vogel Markus: Von M&Ms und bevorzugten Farben: ein handlungsorientierter Unterrichtsvorschlag zur Leitidee „Daten & Zufall“ in der Sekundarstufe I. In:
Stochastik in der Schule 2 (2005), S. 11-18.
Fischer, Gerd: Stochastik einmal anders. Parallel geschrieben mit Beispielen und Fakten,
vertieft durch Erläuterungen. Wiesbaden 2005.
Fischer, Gerd; Lehner, Matthias; Puchert, Angela: Einführung in die Stochastik. Die grundlegenden Fakten mit zahlreichen Erläuterungen, Beispielen und Übungsaufgaben. Wiesbaden 2015 (Mathematik für das Lehramt).
Freudenthal, Hans: Mathematik als pädagogische Aufgabe. Bd. 2. Stuttgart 1973.
Freudenthal, Hans: The Empirical Law of Large Numbers. In: Educational Studies in Mathematics 4 (1972), S. 484-490.
Freudenthal, Hans: Wahrscheinlichkeit und Statistik. München 1975.
151
Führer, Lutz: Misstrauensregeln. In: Mathematik lehren. Erfolgreich unterrichten. Konzepte
und Materialien 85 (1997), S. 61-64.
Gallin, Peter: Prädikatives und funktionales Denken in der Wahrscheinlichkeitsrechnung.
In: ZDM-The International Journal on Mathematics Education 3 (2003), S. 110-119.
Gigerenzer, Gerd: Das Einmaleins der Skepsis. Über den richtigen Umgang mit Zahlen und
Risiken. Berlin 2004.
Gigerenzer, Gerd: Die Evolution des statistischen Denkens. In: Stochastik in der Schule 2
(2004), S. 2-13.
Gigerenzer, Gerd: Die Evolution des statistischen Denkens. In: Unterrichtswissenschaft.
Zeitschrift für Lernforschung 1 (2004), S. 4-22.
Gigerenzer, Gerd: Die Repräsentation von Information und ihre Auswirkung auf statistisches Denken. In: Hell, Wolfgang; Fiedler, Klaus; Gigerenzer, Gerd (Hg.): Kognitive Täuschungen. Fehl-Leistungen und Mechanismen des Urteilens, Denkens und Erinnerns. Heidelberg 1993, S. 99-129.
Gigerenzer, Gerd; Krauss, Stefan: Statistisches Denken oder statistische Rituale: Was sollte
man unterrichten? In: Borovcnik, Manfred; Engel, Joachim; Wickmann, Dieter (Hg.): Anregungen zum Stochastikunterricht. Hildesheim 2001, S. 53-62.
Gigerenzer, Gerd; Martignon, Laura: Risikokompetenz in der Schule lernen. In: Lernen und
Lernstörungen 2 (2015), S. 96.
Gigerenzer, Gerd; Todd, Peter: Simple Heuritics makes us smart. New York 1999.
Glickman, Leslie: Warum man historische Notizen in den Stochastik-Unterricht einbauen
sollte. In: Stochastik in der Schule 3 (1989), S. 43-46.
Götz, Stefan; Humenberger, Hans: Das Problem des anderen Kindes. In: MU. Der Mathematikunterricht 1 (2008), S. 50-60.
Griesel, Heinz (Hg.): Elemente der Mathematik. Leistungskurs Stochastik. Braunschweig
2010.
Hacking, Ian: The emergence of probability: a philosophical study of early ideas about probability, induction and statistical inference. Cambridge 1975 (Cambridge paperback library).
Haftendorn, Dörte: Mathematik sehen und verstehen. Schlüssel zur Welt. Heidelberg, Berlin
2016.
152
Hefendehl-Hebeker, Lisa: Didaktik der Stochastik I: Wahrscheinlichkeitsrechnung, Vorlesungsausarbeitung Hefendehl-Hebeker. Duisburg 2003.
Henze, Norbert: Stochastik für Einsteiger. Eine Einführung in die faszinierende Welt des
Zufalls. Wiesbaden 2013.
Hergel, Wilfried: Wahrscheinlich? Zufall? Wahrscheinlicher Zufall. In: Mathematik lehren.
Erfolgreich unterrichten. Konzepte und Materialien 85 (1997), S. 4–8.
Heymann, Hans W.: Allgemeinbildender Mathematikunterricht – was könnte das sein? In:
Mathematik lehren. Erfolgreich unterrichten. Konzepte und Materialien 33 (1989), S. 4–9.
Hußmann, Stephan; Prediger Schüleranne: Je größer die Wurfanzahl, desto sicherer die
Wette – Mit dem Spiel Wettkönig den Zufall auf lange Sicht erkunden. In: Praxis der Mathematik in der Schule 25 (2009), S. 24-30.
Ineichen, Robert: Modellbildung von Zufallsphänomenen im Laufe der Geschichte. In: MU.
Der Mathematikunterricht 6 (1990), S. 41-49.
Ineichen, Robert: Wie könnte man auf der Oberstufe des Gymnasiums in die schließende
Statistik einführen. In: Didaktik der Mathematik 3 (1982), S. 165-182.
Ineichen, Robert: Würfel und Wahrscheinlichkeit. Stochastisches Denken in der Antike.
Heidelberg 1996.
Israel, Stephan: „Was hat Aids mit Mathe zu tun?" Hinführung zum Satz von Bayes mit
offenen Materialien. In: Mathematik lehren. Erfolgreich unterrichten. Konzepte und Materialien 104 (2001), S. 62-66.
Jahnke, Hans-Niels: Beweisen und hypothetisch-deduktives Denken. In: MU. Der Mathematikunterricht 5 (2007), S. 10-21.
Jahnke, Thomas: Drei Türen, zwei Ziegen und eine Frau. Ein didaktisches Lehrstück? In:
Mathematik lehren. Erfolgreich unterrichten. Konzepte und Materialien 85 (1997), S. 47–
51.
Kahneman, Daniel; Tversky, Amos: On the Psychology of Prediction. In: Psychological Review 80 (1973), S. 237-251.
Kahneman, Daniel: Schnelles Denken, Langsames Denken. München 2012.
Kilian, Hans: Fundierung des Begriffs der stochastischen Unabhängigkeit zufälliger Ereignisse. In: Stochastik in der Schule 2 (1986), S. 13-24.
153
Krämer, Walter: Denkste! Trugschlüsse aus der Welt des Zufalls und der Zahlen. Frankfurt
1995.
Krauss, Stefan: Wahrscheinlichkeit und Intuition - Zwei Seiten einer Medaille? In: Borovcnik, Manfred; Engel, Joachim; Wickmann, Dieter (Hg.): Anregungen zum Stochastikunterricht. Hildesheim 2001, S. 139-146.
Krauss, Stefan: Wie man das Verständnis von Wahrscheinlichkeiten verbessern kann: Das
"Häufigkeitskonzept". In: Stochastik in der Schule 1 (2003), S. 2-9.
Krauss, Stefan; Atmaca, Silke: Wie man Schülern Einsicht in schwierige stochastische Probleme vermitteln kann. Eine Fallstudie über das „Drei-Türen-Problem“. In: Unterrichtswissenschaft. Zeitschrift für Lernforschung 32 (2004), S. 38-57.
Krauss, Stefan; Bruckmeister, Georg: Eignet sich die Formel von Bayes für Gerichtsverfahren? In: Sproesser, Ute; Wessolowski, Silvia; Wörn, Claudia: Daten, Zufall und der Rest der
Welt. Wiesbaden 2014, S. 123-132.
Krauss, Stefan; Wassner, Christoph: Wie man das Testen von Hypothesen einführen sollte.
In: Stochastik in der Schule 1 (2001), S. 29-34.
Kurz-Milcke, Elke; Gigerenzer, Gerd; Martignon, Laura: Risiken durchschauen: Grafische
und analoge Werkzeuge. In: Stochastik in der Schule 1 (2011), S. 8-16.
Kütting, Herbert: Didaktik der Stochastik. Mannheim 1994 (Lehrbücher und Monographien
zur Didaktik der Mathematik, Bd. 23).
Kütting, Herbert: Stochastik im Mathematikunterricht-Herausforderung oder Überforderung? In: MU. Der Mathematikunterricht 6 (1990), S. 5-19.
Kütting, Herbert; Sauer, Martin; Padberg, Friedhelm: Elementare Stochastik. Mathematische Grundlagen und didaktische Konzepte. Berlin, Heidelberg 2011 (Mathematik Primarstufe und Sekundarstufe I + II).
Lakomo, Ewa: Lokale Modelle im Stochastik-Unterricht. In: Stochastik in der Schule 3
(1990), S. 8-21.
Laplace, Pierre-Simon de: A philosophical essay on probabilities (F.W Truscott & F.L.
Emory, Transl.). New York 1951 (Orig. Arbeit 1814 veröff.).
Latten, Stephan; Martignon, Laura; Monti, Marco; Multmeiers, Jan: Die Förderung erster
Kompetenzen für den Umgang mit Risiken bereits in der Grundschule: ein Projekt von RIKO
-STAT und dem Harding Center. In: Stochastik in der Schule 1 (2011), S. 17-25.
154
Lehn, Jürgen; Roes, Henrik: Probleme beim Aufstellen in der Stochastik. In: MU. Der Mathematikunterricht 6 (1990) , S. 29-40.
Lergenmüller, Arno (Hg.): Mathematik Neue Wege. Stochastik. Braunschweig 2012.
Lind, Detlef: Zum Wahrscheinlichkeitsbegriff in der Sekundarstufe I. In: Mathematica didactica 15 (1992), S. 34-47.
Malle, Günther; Malle, Sonja: Was soll man sich unter einer Wahrscheinlichkeit vorstellen?
In: Mathematik lehren. Erfolgreich unterrichten. Konzepte und Materialien 118 (2003), S.
52-56.
Mathea, Barbara (Hg.): Lehrplan Mathematik. Grund- und Leistungsfach in der gymnasialen
Oberstufe (Mainzer Studienstufe). Mainz 2014.
Meyer, Jörg: Stochastik wirklich verstehen. In: MU. Der Mathematikunterricht 1 (2016), S.
17-25.
Mittag, Hans-Joachim: Statistik. Eine Einführung mit interaktiven Elementen. Berlin, Heidelberg 2016.
Pfeifer, Dietmar: Unabhängige Ereignisse in diskreten Wahrscheinlichkeitsmodellen. In:
Stochastik in der Schule 2 (1992), S. 3-20.
Pinkernell, Guido: Test positiv – Diagnose negativ 50. Medizinische Testergebnisse richtig
interpretieren. In: Mathematik lehren. Erfolgreich unterrichten. Konzepte und Materialien
138 (2006), S. 50-55.
Prediger, Schüleranne: Do you want me to do it with probability or normal with my normal
thining? Horizontal and vertical views on the formation of stochastic conceptions. In: International Electronic Journal of Mathematics Education 3 (2008), S. 126-154.
Prediger, Schüleranne: „Auch will ich Lernprozesse beobachten, um besser Mathematik zu
verstehen.“ Didaktische Rekonstruktion als mathematikdidaktischer Forschungsansatz zur
Restrukturierung von Mathematik. In: Mathematica didactica 2 (2005), S. 23-47.
Quinn, Robert; Wiest, Lyndia: Ein konstruktivistischer Zugang zu Permutationen und Kombinationen. In: Stochastik in der Schule 2 (1999), S. 15-19.
Randow, Gero von: Das Ziegenproblem. Denken in Wahrscheinlichkeiten. Reinbek bei
Hamburg 2012.
155
Riemer, Wolfang: Stochastische Probleme aus elementarer Sicht. Mannheim 1991 (Lehrbücher und Monographien zur Didaktik der Mathematik, Bd. 18).
Riemer, Wolfgang: Anmerkung zu Buth: Die Behinderung des gesunden Menschenverstandes durch Stochastik. In: Stochastik in der Schule 3 (1991), S. 23.
Riemer, Wolfgang: Mit Bleistiften würfeln. Beurteilende Statistik zwischen Realität und Simulation. In: Praxis der Mathematik 43 (2012), S. 30-36.
Schanz, Rainer: Statistik und Wahrscheinlichkeitsrechnung. Handreichungen zum Grundkurs der MSS. Mainz 1976.
Schmidt, Günther: Schwächen im gegenwärtigen Stochastikunterricht und Ansätze zu ihrer
Behebung. MU. Der Mathematikunterricht 6 (1990), S. 20-28.
Schnell, Schüleranne: Muster und Variabilität erkunden. Konstruktionsprozesse kontextspezifischer Vorstellungen zum Phänomen Zufall (Dortmunder Beiträge zur Entwicklung und
Erforschung des Mathematikunterrichts Bd. 14).
Schnell, Schüleranne; Prediger, Schüleranne: From “everything changes” to “for high numbers, it changes just a bit” – Theoretical notions for a microanalysis of conceptua change
processes in stochastic contexts. In: ZDM-The International Journal on Mathematics Education 44 (2012), S. 825-840.
Schrade, Georg: Schwierigkeiten mit stochastischer Modellbildung-zwei Beispiele aus der
Praxis. In: Journal für Mathematikdidaktik 1 (1980), S. 86-101.
Schupp, Hans: Das Galtonbrett im stochastischen Anfangsunterricht. In: Mathematik lehren.
Erfolgreich unterrichten. Konzepte und Materialien 12 (1985), S. 12–16.
Schupp, Hans: Zum Verhältnis statistischer und wahrscheinlichkeitstheoretischer Komponenten im Stochastik-Unterricht der Sekundarstufe I. In: Journal für Mathematikdidaktik 3
(1982), S. 207-226.
Sedlmeier, Peter: Statistik ohne Formeln. In: Borovcnik, Manfred; Engel, Joachim; Wickmann, Dieter (Hg.): Anregungen zum Stochastikunterricht. Hildesheim 2001, S. 83-97.
Sedlmeier, Peter: Wie kann Intuition in der Statistikausbildung helfen? In: Sproesser, Ute;
Wessolowski, Silvia; Wörn, Claudia: Daten, Zufall und der Rest der Welt. Wiesbaden 2014,
S. 223-235.
Sedlmeier, Peter; Gigerenzer, Gerd: Teaching Bayesian Reasoning in Less Than Two Hours.
In: Journal of Experimental Psychology 3 (2001), S. 380-400.
156
Sekretariat der Ständigen Konferenz der Kultusminister der Länder in der Bundesrepublik
Deutschland: Bildungsstandards im Fach Mathematik für die Allgemeine Hochschulreife
(Beschluss der Kultusministerkonferenz vom 18.10.2012). Berlin 2012.
Sill, Hans-Dieter: Zur Modellierung zufälliger Erscheinungen. In: Stochastik in der Schule
3 (2010), S. 2-13.
Spandaw, Jeroen: Was bedeutet der Begriff „Wahrscheinlichkeit“? In: Rathgeb, Martin; Helmerich, Markus Alexander; Krömer, Ralf; Lengnink, Katja; Nickel, Gregor (Hg.): Mathematik im Prozess. Philosophische, Historische und Didaktische Perspektiven. Wiesbaden
2013, S. 41-56.
Steinbring, Heinz: Mathematische Begriffe in didaktischen Situationen: das Beispiel der
Wahrscheinlichkeit. In: Journal für Mathematik-Didaktik 2 (1985), S. 85-118.
Steinbring, Heinz: Wahrscheinlichkeit als allgemeine Messtheorie Vorschläge für eine didaktische Konzeption des Entwicklungsprozesses der Wahrscheinlichkeit. In: Dörfler, Willibald; Fischer, Hans (Hg.): Stochastik im Schulunterricht. Wien, Stuttgart 1991 (Schriftenreihe Didaktik der Mathematik, Bd. 3), S. 223-230.
Steinbring, Heinz: Zur Entwicklung des Wahrscheinlichkeitsbegriffs. Das Anwendungsproblem in der Wahrscheinlichkeitstheorie aus didaktischer Sicht. Bielefeld 1980 (Materialien und Studien. Institut für Didaktik der Mathematik der Universität Bielefeld, Bd. 18).
Strick, Heinz K.: Vorstellungen von Schülerinnen und Schülern über Zufallsvorgänge. In:
Mathematik lehren. Erfolgreich unterrichten. Konzepte und Materialien 85 (1997), S. 52-54.
Székely, Gábor J.: Paradoxa: klassische und neue Überraschungen aus Wahrscheinlichkeitsrechnung und mathematischer Statistik. Thun 1990.
Tietze, Uwe-Peter; Klika, Manfred; Wolpers, Hans: Didaktik des Mathematikunterrichts in
der Sekundarstufe II. Braunschweig 1982 (Didaktik der Mathematik).
Tschirk, Wolfgang: Statistik: Klassisch oder Bayes. Zwei Wege im Vergleich. Berlin, Heidelberg 2014.
Ullmann, Philipp: Diagramme, die uns etwas angehen. In: MU. Der Mathematikunterricht 4
(2012), S. 53-59.
Vanscó, Ödön; Warmuth, Elke: Schwierigkeiten mit dem Stabilwerden der relativen Häufigkeiten - Das
1
- Gesetz. In: Stochastik in der Schule 2 (1998), S. 22-43.
√n
157
Vascó, Ödön: Parallel Discussion of classical and bayesian ways as an introduction to statistical inference. In: Mathematics Education 3 (2009), S. 291-322.
Walter, Harald: Heuristische Strategien und Fehlvorstellungen in stochastischen Situationen.
In: MU. Der Mathematikunterricht 1 (1983), S. 11-18.
Wassner, Christoph; Biehler, Rolf: Förderung Bayesianischen Denkens-Kognitionspsychologische Grundlagen und didaktische Analysen. Kassel 2007 (Kasseler Schriften zur Didaktik der Stochastik, Bd. 4).
Wassner, Christoph; Biehler, Rolf; Martignon, Laura: Das Konzept der natürlichen Häufigkeiten im Stochastikunterricht. In: MU. Der Mathematikunterricht 3 (2007), S. 33-44.
Wassner, Christoph; Biehler, Rolf; Schweynoch, Stefan: Authentisches Bewerten und Urteilen unter Unsicherheit - Arbeitsmaterialien und didaktische Kommentare für den Themenbereich “Bayessche Regel” für den Stochastikunterricht der Sekundarstufe I. Kassel 2007
(Kasseler Schriften zur Didaktik der Stochastik, Bd. 5).
Wassner, Christoph; Martignon, Laura; Biehler, Rolf: Bayesianisches Denken in der Schule.
In: Unterrichtswissenschaft. Zeitschrift für Lernforschung 1 (2004), S. 58-96.
Weustenfeld, Wolfram: Die Augensumme zweier Würfel voraussagen: Alles nur eine Frage
von Glück oder Pech? In: Stochastik in der Schule 3 (2007), S. 2-15.
Wickmann, Dieter: Bayes-Statistik: Einsicht gewinnen und entscheiden bei Unsicherheit.
Mannheim 1990 (Mathamtische Texte, Bd. 4).
Wickmann, Dieter: Der Theorieneintopf ist zu beseitigen. Ereignis- und Zustandswahrscheinlichkeit-Versuch einer Klärung des Wahrscheinlichkeitsbegriffs zum Zwecke einer
Methodenbereinigung. In: Borovcnik, Manfred; Engel, Joachim; Wickmann, Dieter (Hg.):
Anregungen zum Stochastikunterricht. Hildesheim 2001, S.123-132.
Wickmann, Dieter: Zur Begriffsbildung im Stochastikunterricht. In: Journal für Mathematik-Didaktik 1 (1998), S. 46-80.
Winter, Heinrich: Zur intuitiven Aufklärung probabilistischer Paradoxien. In: Journal für
Mathematik-Didaktik 13 (1992), S. 23-53.
Wirths, Helmut: Die Geburt der Stochastik. In: Stochastik in der Schule 3 (1999), S. 3-30.
Wirths, Helmut: Ein Harmonietest-Die ersten Stunden. In: Stochastik in der Schule 1 (1998),
S. 5-16.
158
Wittmann, Erich C.: Grundfragen des Mathematikunterrichts. Wiesbaden 2009 (Studium
Klassiker).
Wollring, Bernd: Ein Beispiel zur Konzeption von Simulationen bei der Einführung des
Wahrscheinlichkeitsbegriffs. In: Stochastik in der Schule 3 (1992), S. 2-25.
Würfelmöglichkeiten.
In:
Landungsbildungsserver
Baden-Württemberg.
URL:
http://www.schule-bw.de/unterricht/faecher/mathematik/3material/sek1/zufall/grafik1.gif
(Abgerufen: 08.06.2016, 11:32 UTC).
Zimmermann, Marc; Gundlach, Martin: Wie Ziegen zum Hauptgewinn werden können. In:
Sproesser, Ute; Wessolowski, Silvia; Wörn, Claudia: Daten, Zufall und der Rest der Welt.
Wiesbaden 2014, S. 315-325.
159
160