Kapitel 10 Analytische Geometrie, Vektor- und Matrixrechnung

Kapitel 10
Analytische Geometrie, Vektorund Matrixrechnung
10.1
Koordinatensysteme
Eine Gerade, eine Ebene oder den Anschauungsraum beschreibt man durch Koordinatensysteme.
10.1.1
Was sind Koordinatensysteme?
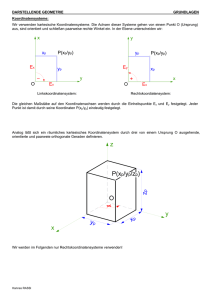
Es gibt affine Koordinatensysteme
(Koordinaten x, y oder x1, x2 in der Ebene,
x, y, z oder x1, x2, x3 im Raum )
(Tafelskizzen!)
kartesische Koordinatensysteme
(Tafelskizzen!)
Polarkoordinatensysteme (in der Ebene)
(Koordinaten r, φ)
(Tafelskizze!)
und viele weitere Koordinatensysteme.
1
10.1.2
Wozu sind Koordinatensysteme gut?
Durch ein affines oder kartesisches Koordinatensystem werden eineindeutig aufeinander abgebildet:
• die Punkte einer Geraden und die Punkte von R
oder
• die Punkte einer Ebene und die Punkte von R2
oder
• die Punkte des Raumes und die Punkte von R3.
Dadurch kann man
(a) geometrische Probleme durch Rechnung lösen
und
(b) rechnerische Probleme geometrisch deuten.
10.1.3
Die Raumzeit der Mechanik
Beschreibt man Punkte im Raum durch kartesische
Koordinaten (x, y, z), und hängt man daran als vierte Koordinate die Zeit t, so erhält man die vierdimensionale Raum-Zeit mit Punkten, die beschrieben werden durch (x, y, z, t).
Damit gelang Minkowski 1908 eine überraschend einfache Beschreibung der speziellen Relativitätstheorie.
2
10.2
Einfache Vektorrechnung
10.2.1
Was ist ein Vektor?
Ein Vektor ~x im Rn, n ∈ N, z.B. n = 2, 3, 4, ist ein
n-Tupel reeller Zahlen (x1,
x2 , . . 
. , xn), manchmal
x1
 x2 
 
 . 

auch geschrieben als Spalte 
 . .
 
 . 
xn
Für n = 2 schreibt man oft x, y statt x1, x2.
Für n = 3 schreibt man oft x, y, z statt x1, x2, x3.
10.2.2
Vektoraddition und Multiplikation mit Skalaren
Vektoraddition und Vektorsubtraktion werden komponentenweise

 
   definiert:
x1 ± y1
y1
x1
 x2   y2   x2 ± y2 

    

 .   .  
.
.
   
~x ± ~y = 

 . ± . =
.

    

 .   .  
.
yn
xn ± yn
xn
(Tafelskizze für n = 2, 3 bei affinem Koordinatensystem!)
Parallelogrammregel
Multiplikation eines Vektors mit einem Ska3
lar (mit einer rellen Zahl) wird komponentenweise
definiert:
  

x1
cx1
 x2   cx2 
  

 .   . 
 

c~x = c 
 .  =  . .
  

 .   . 
xn
cxn
(Tafelskizze bei affinem Koordinatensystem!)
Negatives c kehrt die Richtung
  um!
0
0
 
.

Für den Nullvektor ~o = 
 .  gilt offenbar:
 
.
0
n
~x + ~o = ~o + ~x = ~x ∀~x ∈ R .
~y 6= ~o heißt parallel zu ~x 6= ~o, ~x k ~y :⇔ ~x = c~y
mit c ∈ R.
Vektoren ~a1, ~a2, . . . , ~ak heißen linear abhängig,
wenn für mindestens ein i mit 1 ≤ i ≤ k gilt:
ai =
k
X
cj~aj .
j=1,j6=i
Sonst heißen ~a1, ~a2, . . . , ~ak linear unabhängig.
Das ist genau dann der Fall, wenn gilt:
4
k
X
ck~ak = ~o ⇒ c1 = c2 = . . . = ck = 0.
j=1
10.2.3
Matrizen und Matrixprodukt
Eine Matrix ist ein rechteckiges Schema reeller Zahlen.
Ist


a11 a12 . . . a1n
 a21 a22 . . . a2n 
,
A=
 ...

am1 am2 . . . amn


b11 b12 . . . b1k
 b21 b22 . . . b2k 
,
B=
 ...

bn1 bn2 . . . bnk
so ist AB die Matrix, in deren p-ter Zeile und qter
Spalte das Element
cpq =
n
X
apibiq
i=1
steht.
Schreibweise: Für einen Spaltenvektor ~x schreiben wir auch:
~x = (x1, x2, . . . , xn)T
5
oder
~xT = (x1, x2, . . . , xn).
10.2.4
Basis
{~b1, ~b2, . . . , ~bn} bilden eine Basis des Rn, wenn
gilt: ~b1, ~b2, . . . , ~bn sind linear unabhängig und
∀~x ∈ Rn∃x1, x2, . . . , xn : ~x = x1~b1 + . . . + xn~bn.
Eine spezielle Basis des Rn besteht aus






1
0
0
 0 
 1 
 0 




.
~e1 := 
, ~e2 := 
, . . . , ~en := 



...
...
... 
0
0
1
Offenbar gilt ∀~x ∈ Rn: ~x = x1~e1 + . . . + xn~en.
10.2.5
Skalarprodukt, Länge, Winkel
Das Skalarprodukt zweier Vektoren ~x, ~y ist für
uns
~x · ~y = x1y1 + x2y2 + . . . + xnyn.
(Andere Schreibweisen: ~x~y , < ~x, ~y >, s(~x, ~y ) oder
auch ~xT ~y .
Aber ~x~y T ist etwas Anderes!)
Für ~x = ~y : ~x~x = ~x2.
Offenbar gilt: ~x~y = ~y~x, (c~x)~y = ~x(c~y ) = c(~x~y ).
6
Offenbar gilt: ~e2i = 1, ~ei~ek = 0, falls i 6= k.
Durch Rechnung zeigt man das Distributivgesetz:
~x(~y + ~z) = ~x~y + ~x~z.
Die Länge eines Vektors ~x ist für uns
√
|~x| = ~x · ~x.
Es gilt: |~o| = 0.
|~v | = 1 ⇔ ~v Einheitsvektor
Für Vektoren im Rn gilt die Dreiecksungleichung:
|~x ± ~y | ≤ |~x| + |~y |.
Der Winkel ∠(~x, ~y ) zweier Vektoren ~x 6= ~o 6= ~y ist
definiert durch
~x · ~y
.
|x| · |y|
Damit gilt ~x und ~y sind zueinander orthogonal,
normal oder senkrecht, in Zeichen
cos ∠(~x, ~y ) =
~x ⊥ ~y ⇔ ~x~y = 0.
10.2.6
Vektorprodukt im R3
Für ~x, ~y ∈ R3 ist das Vektorprodukt ~x × ~y von
~x und ~y :
7
~x × ~y = (x2y3 − x3y2, x3y1 − x1y3, x1y2 − x2y1)T .
Offenbar gilt: (c~x) × ~y = ~x × (c~y ) = c(~x × ~y ),
~y × ~x = −~x × ~y , und damit auch:
∀c ∈ R : ~x × (c~x) = ~o.
Man kann zeigen:
~x(~x × ~y ) = 0.
~x × ~y ist also orthogonal zu ~x und zu ~y .
Man kann zeigen, dass gilt:
~x × (~y + ~z) = ~x × ~y + ~x × ~z
und
~x × ~y = ~o ⇔
~x = ~o oder ~y = ~o oder ~x = c~y mit c 6= 0.
Es gilt also:
~x × ~y = ~o, ~x 6= ~o, ~y 6= ~o ⇒ ~x = c~y mit c 6= 0.
Man kann zeigen:
|~x × ~y |2 = |~x|2|~y |2 − |~x~y |2.
Vorsicht! × ist nicht assoziativ. Im allgemeinen
gilt:
~x × (~y × ~z) 6= (~x × ~y ) × ~z.
8
10.2.7
Das Spatprodukt im R3
~x(~y × ~z) =: (~x, ~y , ~z)
heißt das Spatprodukt der Vektoren ~x, ~y , ~z.
Man kann zeigen: (~x, ~y , ~z) = (~y , ~z, ~x) = (~z, ~x, ~y ) =
−(~x, ~z, ~y ) = −(~z, ~y , ~x) = −(~y , ~x, ~z).
Wegen ~x × ~x = ~o gilt: Sind zwei Vektoren in einem
Spatprodukt gleich, so verschwindet das Spatprodukt.
10.3
Anwendung auf die Geometrie im Anschauungsraum
10.3.1
Punkte und Vektoren
Punkte A, B, . . . , X, Y, . . .
Vektoren ~a, ~b, . . . , ~x, ~y . . . .
Vektoren kann man addieren, Punkte nicht!
c~x ist sinnvoll, cX ist sinnlos!
10.3.2
Koordinatenvektoren
Bezüglich eines affinen xyz-Koordinatensystems
mit einem Koordinatenursprung (kurz: Ursprung
O ist jedem Punkt P sein Koordinatenvektor
oder Ortsvektor p~ = (x, y, z)T eineindeutig zugeordnet.
(Tafelskizze!)
9
Der Verbindungsvektor P~Q der Punkte P (~p)
und Q(~q) ist P~Q = ~q − p~.
(Tafelskizze!)
Ist P ein Punkt und ~v ein Vektor, so gibt es genau
einen Punkt Q, so dass gilt: ~v = P~Q.
10.3.3
Abstand von Punkten
Liegt ein kartesisches Koordinatensystem zu Grunde, so gilt: Der Abstand der Punkte P (~p), Q(~q) ist
d(P, Q) = |~q − p~|.
10.3.4
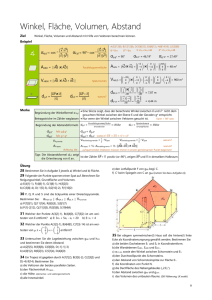
Spatvolumen
Mitteilung: Das Volumen V des Spats mit einer
Ecke P , der aufgespannt wird von den Vektoren
~x, ~y , ~z, ist das Spatprodukt dieser Vektoren:
V (~x, ~y , ~z) = |(~x, ~y , ~z)|,
falls z.B. ein kartesisches Koordinatensystem zu Grunde gelegt wurde.
Mit etwas Geometrie sieht man: Das Volumen V des
Tetraeders mit den Ecken P, Q, R, S ist
1
V (P, Q, R, S) = |(~q − p~, ~r − p~, ~s − p~)|.
6
Sind ~x, ~y linear unabhängig, so gilt: (~x, ~y , ~z) = 0 ⇔
~x, ~y , ~z liegen in der Ebene, die von ~x, ~y aufgespannt
10
wird ⇔ ~z ist parallel zur Ebene, die von ~x, ~y aufgespannt wird.
10.3.5
Winkel von Vektoren
Mitteilung: Was im Rn als Winkeldefinition diente,
~x · ~y
,
cos ∠(~x, ~y ) =
|x| · |y|
liefert im Anschauungsraum tatsächlich den bekannten Winkel der Elementargeometrie,
falls ein kartesisches Koordinatensystem zu
Grunde liegt.
10.3.6
Zum Vektorprodukt
Mitteilung: Liegt ein kartesisches Rechts-Koordinatensystem zugrunde,
bei dem x-, y- und z-Achse liegen wie Daumen, Zeigefinger und Mittelfinger einer rechten Hand,
so gilt: Sind ~v , w
~ linear unabhängige Vektoren, so
ist
~v × w
~ ⊥ ~v , w,
~
(1)
|~v × w|
~ = |~v | · |w|
~ · sin ∠(~v , w),
~
(2)
und in der angegebenen Reihenfolge gilt:
~v , w,
~ ~v × w
~ bilden ein Rechtssystem.
(3)
Durch (1), (2), (3) ist ~v × w
~ eindeutig bestimmt.
11
10.3.7
Geraden
Die Verbindungsgerade P Q zweier Punkte P ,
Q hat die Parameterdarstellung
~x = p~ + t(~q − p~), t ∈ R.
(Tafelskizze!)
Ist ~x = p~ + t~v , t ∈ R, eine Parameterdarstellung
einer Geraden g, so heißt ~v ein Richtungsvektor
von g.
10.3.8
Ebenen
Die Verbindungsebene P QR dreier Punkte P ,
Q, R hat die Parameterdarstellung
~x = p~ + t(~q − p~) + s(~r − p~), t, s ∈ R.
(Tafelskizze!)
Ist
~x = p~ + t~v + sw,
~
t, s ∈ R,
(1)
eine Parameterdarstellung einer Ebene ε, so heißen
~v , w
~ Richtungsvektoren von ε.
Ist ~n senkrecht zu ε, so ist ~n(~q − p~) = ~n(~r − ~n) = 0,
also
ε : ~n~x = ~np~
eine Gleichung der Ebene ε.
(Tafelskizze!)
Eine Gleichung von ε erhält man also aus (1) durch:
(~v × w)
~ · (~x − p~) = 0.
12
Ist umgekehrt ax + by + cz = d die Gleichung einer
Ebene ε, so ist (a, b, c)T ein Normalenvektor von
ε.
Ist |~n| = 1 und ~np~ ≥ 0, so heißt die Gleichung
~n~x − ~np~ = 0
die Hesse-Form der Ebenengleichung.
Mitteilung: Setzt man ~q in die linke Seite der Hesseform von ε ein, so erhält man den vorzeichenbehafteten Abstand des Punktes Q(~q) von der
Ebene ε.
10.3.9
Winkel von Geraden
Der Winkel von Geraden g und h mit Richtungsvektoren ~v und w
~ ist der Winkel der Vektoren ~v und
w.
~
10.3.10
Winkel von Gerade und Ebene
Der Winkel ∠(g, ε) einer Geraden g mit Richtungsvektor ~r zu einer Ebene ε mit Normalenvektor ~n ist
definiert als Winkel von g zur Schnittgeraden von ε
mit derjenigen Ebene ν, die g enthält und parallel
ist zu ~n.
(Tafelskizze!)
Ist ν nicht definiert, also g k ~n, so ist ∠(g, ε) = π2 .
Zur Berechnung: Es gilt:
∠(g, ε) = π2 − ∠(g, ~n),
13
(Tafelskizze!) also
·~n
sin ∠(g, ε) = |~r~r|·|~
n| .
10.3.11
Schnitt Gerade - Ebene
Gerade g: ~x = p~ + t · ~v , t ∈ R;
(1)
Ebene ε: ~n · ~x − d = 0.
Schnittpunkt S(~s): ”~x einsetzen in ε“
0 = ~n ·~x − d = ~n · (~p + t ·~v ) − d = ~n · p~ + t~n ·~v − d ⇒
d − ~n · p~
~n · ~v
einsetzen in (1) liefert S:
t=
~s = p~ +
10.3.12
d − ~n · p~
· ~v .
~n · ~v
Schnitt Ebene - Ebene
ε: ax + by + cz = d
(1)
δ: px + qy + rz = s
(2)
Schnittgerade g?
(1), (2) ist ein Beispiel eines linearen Gleichungssystems mit zwei Gleichungen, drei Unbekannten.
Ist a 6= 0, so kann man x aus (2) eliminieren:
(2) − ap · (1): (q − pba )y + (r − pca )z = s − pd
a,
kurz: q 0y + r0z = s0.
Ist q 0 6= 0, so kann man ausrechnen:
0
0
y = − qr0 z + qs0 =: r00z + s00.
14
x = − ab y − ac z + ad =: b0(r00z + s00) + c0z + d0 =
(b0r00 + c0)z + (b0s00 + d0) =: b00z + d00.
Dabei ist z ∈ R beliebig.
⇒ Parameterdarstellung von g:
 00 
 00 
b
d
t ∈ R.
~x =  s00  + t ·  r00  ,
1
0
Dabei war a 6= 0 6= q 0.
15