log n wurzel

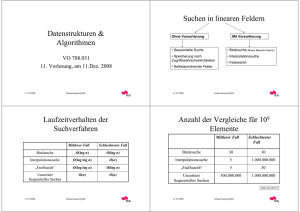
Datenstrukturen &
Algorithmen
VO 708.031
11. Vorlesung, am 11.Dez. 2008
11.12.2008
helmut.hauser@IGI
Suchen in linearen Feldern
Ohne Vorsortierung
Mit Vorsortierung
• Sequentielle Suche
• Binärsuche (Binary Bisection Search)
• Speicherung nach
Zugriffswahrscheinlichkeiten
• Interpolationssuche
• Fastsearch
• Selbstanordnende Felder
11.12.2008
helmut.hauser@IGI
Laufzeitverhalten der
Suchverfahren
Mittlerer Fall
Schlechtester Fall
Binärsuche
O(log n)
O(log n)
Interpolationssuche
O(log log n)
O(n)
„FastSearch“
O(log log n)
O(log n)
Unsortiert
Sequentielles Suchen
O(n)
O(n)
11.12.2008
helmut.hauser@IGI
Anzahl der Vergleiche für 109
Elemente
Mittlerer Fall
Schlechtester
Fall
Binärsuche
30
30
Interpolationssuche
5
1.000.000.000
„FastSearch“
5
30
Unsortiert
Sequentielles Suchen
500.000.000
1.000.000.000
Alles circa Wert !!
11.12.2008
helmut.hauser@IGI
Bäume - Grundlagen
Definition:
Ein Baum ist eine Menge, die durch eine sog.
Nachfolgerrelation strukturiert ist.
Elemente: Knoten
In einem Baum gilt:
1
∃ Knoten w ohne Vater(w) Æ (w=Wurzel)
k
Vater(x)
1
∀ Knoten k≠w ∃ Knotenfolge k0, k1, …, kt
mit k0=k, kt=w und ki=Vater(ki-1) für
i=1, 2, …, t.
(Ast zwischen k und w, Länge t)
11.12.2008
helmut.hauser@IGI
x
Sohn(k)
Anwendungsstrukturen
Chef
Gruppenleiter 1
Mitarbeiter 1
M2
Hierarchische Strukturen
GL 2
GL 3
M3
Inklusionsstrukturen
Buch
Lebewesen
Kap. 1
Kap. 5
Insekten
Tiere
Käfer
Abschn. 1.1
11.12.2008
1.4
helmut.hauser@IGI
Anwendungsstrukturen
– Rekursionsbäume
– Entscheidungsbäume
– Suchbäume
– Haldenbäume
– Codebäume u.v.a.
QUICK(1,n)
QUICK(1,k)
/
Beispiel:
Arithmetische Ausdrücke
Blätter (= Knoten ohne Söhne) enthalten
Zahlen, innere Knoten speichern
Operatoren (+, -, *, /).
*
+
2
11.12.2008
helmut.hauser@IGI
QUICK(k+1,n)
+
3
5
4
3
Binärbäume
Jeder Knoten hat maximal zwei Nachfolger
11.12.2008
helmut.hauser@IGI
Reihenfolge der Knoten
(1) Symmetrische Reihenfolge (SR):
Linker Teilbaum in SR, Wurzel, rechter Teilbaum in SR.
11.12.2008
SR(k)
1: IF k≠nil THEN
2:
SR(LINKS(k))
3:
WRITE k
4:
SR(RECHTS(k))
Leicht rekursiv zu
programmieren.
(Def. übersetzen!)
Aufruf: SR(w)
((2+5)*3)/(4+3)
Infix-Notation
helmut.hauser@IGI
Reihenfolge der Knoten
(2) Hauptreihenfolge (HR):
Wurzel, linker Teilbaum in HR, rechter Teilbaum in HR.
/*+253+43
(3) Nebenreihenfolge (NR):
Linker Teilbaum in NR, rechter Teilbaum in NR, Wurzel.
25+3*43+/
7 21 7 3
11.12.2008
Postfix-Notation
(leichte Auswertung, mit
Stapel)
helmut.hauser@IGI
Sortierte Binärbäume
Sortiert nach SR
15
6
3
2
18
7
17
5
20
13
9
……………….....
11.12.2008
helmut.hauser@IGI
„Fädelung“ der Knoten
Sortierte Binärbäume
Binäre Suche
1: SUCHE(w,k)
2: IF k=nil OR w=WERT(k) THEN
3:
WRITE k
4: ELSE IF w<WERT(k) THEN
5:
SUCHE(w , LINKS(k))
6: ELSE SUCHE(w , RECHTS (k))
O(Höhe)
Weitere Operationen möglich:
Einfügen (Erstellen), Löschen,
Minimum, Maximum, Vorgänger, Nachfolger
11.12.2008
helmut.hauser@IGI
Binärbäume - Zusammenfassung
Binärbäume sind spezielle Bäume, welcher maximal 2 Söhne haben.
Knotenreihenfolgen (Symmetrische, Haupt- und Nebenreihenfolge)
Æ geordneter Binärbaum möglich (Nachfolgerrelation)
Implementierbare Funktionen:
Alle Funktionen:
O(„Baumhöhe“)
11.12.2008
• Minimum
• Maximum
• Vorgänger
• Nachfolger
• Einfügen (Aufbau)
• Löschen
• Suchen
helmut.hauser@IGI
Wörterbuchproblem
Binärbäume - online
Durch Update-Operation
(Löschen, Einfügen)
1
9
Höhe ≠ log(n)
8
Entartet!
3
Höhe = O(n)
Umstrukturieren
O(n)
(fast) ausgeglichen
= gut, da minimale
Höhe = O( log n)
11.12.2008
teuer!
7
4
5
helmut.hauser@IGI
Zur Erhaltung von: Höhe=log(n)
Techniken zur Erhaltung einer logarithmischen Baumhöhe
Höhenbalanciert
Gewichtsbalanciert
h(B)=Höhe des Baums
g(B) = Anzahl der Blätter
Für jeden Knoten k gilt:
Für jeden Knoten k gilt:
|h(Blinks)-h(Brechts)|≤k
1/α ≤ g(Blinks)/g(Brechts)| ≤ α
Bsp: AVL-Bäume (k=1)
BB-Bäume (bounded
balance)
Mehrwegbäume
11.12.2008
helmut.hauser@IGI
Definition:
(2-4)-Bäume
Ein (2-4)-Baum ist ein Baum mit folgenden Eigenschaften:
(1) Alle Äste sind gleich lang.
(2) Die max. Anzahl der Söhne eines Knotens ist gleich 4.
(3) Innere Knoten haben ≥ 2 Söhne.
(4) Die Blätter enthalten v.l.n.r. die Werte aufsteigend sortiert.
(5) Jeder innere Knoten mit t Söhnen (2 ≤ t ≤ 4) speichert t-1
Hilfsinformationen x1, …, xt-1, wobei xi = größter Wert im Teilbaum
des i-ten Sohnes von links.
11.12.2008
helmut.hauser@IGI
(2-4)-Bäume
Höhe=O(log n)
Enthalten nur
Hilfsinformationen.
4,6
1,2
1
2
10,11
5
4
5
6
10
11
24
Daten werden in den Blättern gespeichert.
11.12.2008
helmut.hauser@IGI
(2-4)-Bäume
Wir wollen damit das Wörterbuchproblem lösen:
SUCHEN, EINFÜGEN, ENTFERNEN
Achtung:
Nach den Update-Funktionen (Einfügen, Entfernen)
muss wieder ein korrekter 2-4-Baum vorliegen !
Æ Zeitlicher Mehraufwand, der sich aber rentiert Æ Amortisierte Kosten
siehe später
11.12.2008
helmut.hauser@IGI
(2,4)-Bäume - Suchen
8
2
2
4
4
5
5
11
10
8
10
12
11
12
24
24
Pro Knoten maximal 3 Vergleich Æ O(1)
Æ Höhe garantiert Θ(log n) Æ T(n)=Θ(log n)
11.12.2008
helmut.hauser@IGI
31
(2,4)-Bäume - Einfügen
Definition:
α(k) ist die Ordnung des k-ten Knoten (=Anzahl der Söhne)
Zwei Fälle (nach! dem Einfügen):
1.) Falls α(k) ≤ 4 Æ fertig !!
2.) Falls α(k) > 4 Æ Bedingung verletzt Æ SPALTEN
v
v
k
k
11.12.2008
v’
helmut.hauser@IGI
k’
(2,4)-Bäume - Entfernen
Zwei Fälle (nach dem Entfernen):
1.) Falls α(k) ≥ 2 Æ fertig !!
2.) Falls α(k) < 2 Æ Bedingung verletzt (underflow) Æ
STEHLEN (wenn α(k‘) ≥ 3)
k’
k
oder VERSCHMELZEN (α(k‘) = 2)
STEHLEN
v
k’
11.12.2008
k’
k
v
k
VERSCHMELZEN
helmut.hauser@IGI
k
Analyse der Operationen
Wörterbuchproblem
11.12.2008
Suchen:
Einfügen:
Entfernen:
O(log n)
O(log n)
O(log n)
Speicher:
O(n)
helmut.hauser@IGI
Mischbare Warteschlangen
Definition:
•
•
•
•
EINFÜGEN (S,x)
MAXIMUM (S)
ENTFERNE_MAX (S)
MISCHE (S,S‘)
Halde Æ 3 Operationen in O(log n)
Mischen aber teuer !! Æ O(n)
Mit Baum alle Operation Æ O(log n)
11.12.2008
helmut.hauser@IGI
Mischbare Warteschlangen
9
3
3
-Unsortierter (2,4)-Baum
9
1
9
- innere Knoten speichert
Maximum in seinen Teilbaum
und Zeiger darauf
8
5
Maximum trivial Æ
in Wurzel O(1)
2
6
8
Entferne Maximum Æ Update der
Information O(log n)
8
Einfügen ist
Spezialfall von
Mischen!
5
3
11.12.2008
helmut.hauser@IGI
8
1
5
2
6
8
Mischbare Warteschlangen
Mische (S, S‘): Æ Beides 2-4-Bäume mit der Höhe h und h‘
1.Fall: h = h‘
2.Fall: h > h‘
Neue Wurzel = O(1)
Check α(v) Æ O(log n)!!
v
k
w’
h’
T
11.12.2008
helmut.hauser@IGI
T’
Amortisierte Kosten
2-4-Bäume benötigen zusätzliche Operation, damit sie 2-4-Bäume
bleiben und damit garantiert h=O(log n) besitzen.
Potentielle Laufzeit:
O(m*log(n))
Beobachtung: z.B. nach Spalt-Operation ist der Baum „ausgeglichener“.
Æ Investierte Zeit rentiert sich später Æ Amortisierungsanalyse.
Durchschnittliche Zeit über alle Operation
(in unserem Fall: Einfügen, Löschen) im schlimmsten Fall.
11.12.2008
helmut.hauser@IGI