Trigonometrische Funktionen ( Aufgaben dazu )

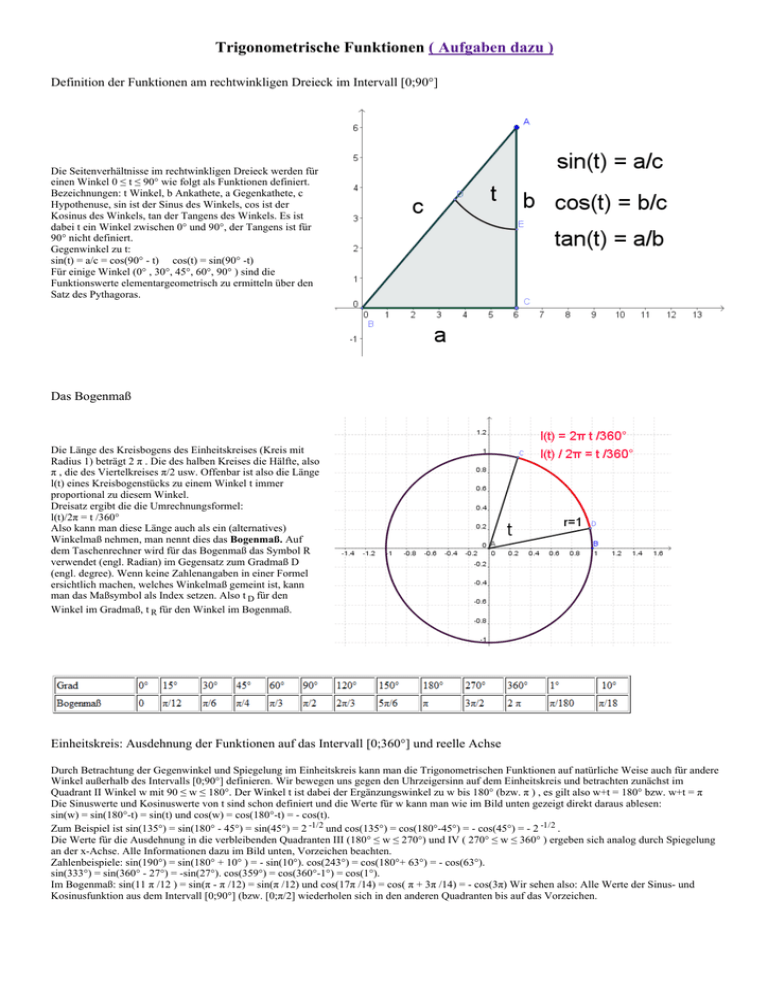
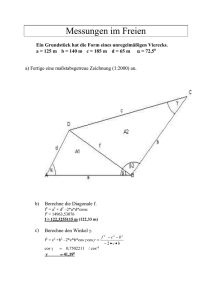
Trigonometrische Funktionen ( Aufgaben dazu )
Definition der Funktionen am rechtwinkligen Dreieck im Intervall [0;90°]
Die Seitenverhältnisse im rechtwinkligen Dreieck werden für
einen Winkel 0 ≤ t ≤ 90° wie folgt als Funktionen definiert. Bezeichnungen: t Winkel, b Ankathete, a Gegenkathete, c
Hypothenuse, sin ist der Sinus des Winkels, cos ist der
Kosinus des Winkels, tan der Tangens des Winkels. Es ist
dabei t ein Winkel zwischen 0° und 90°, der Tangens ist für
90° nicht definiert. Gegenwinkel zu t: sin(t) = a/c = cos(90°  t) cos(t) = sin(90° t) Für einige Winkel (0° , 30°, 45°, 60°, 90° ) sind die
Funktionswerte elementargeometrisch zu ermitteln über den
Satz des Pythagoras.
Das Bogenmaß
Die Länge des Kreisbogens des Einheitskreises (Kreis mit
Radius 1) beträgt 2 π . Die des halben Kreises die Hälfte, also
π , die des Viertelkreises π/2 usw. Offenbar ist also die Länge
l(t) eines Kreisbogenstücks zu einem Winkel t immer
proportional zu diesem Winkel. Dreisatz ergibt die die Umrechnungsformel: l(t)/2π = t /360° Also kann man diese Länge auch als ein (alternatives)
Winkelmaß nehmen, man nennt dies das Bogenmaß. Auf
dem Taschenrechner wird für das Bogenmaß das Symbol R
verwendet (engl. Radian) im Gegensatz zum Gradmaß D
(engl. degree). Wenn keine Zahlenangaben in einer Formel
ersichtlich machen, welches Winkelmaß gemeint ist, kann
man das Maßsymbol als Index setzen. Also t D für den
Winkel im Gradmaß, t R für den Winkel im Bogenmaß.
Einheitskreis: Ausdehnung der Funktionen auf das Intervall [0;360°] und reelle Achse
Durch Betrachtung der Gegenwinkel und Spiegelung im Einheitskreis kann man die Trigonometrischen Funktionen auf natürliche Weise auch für andere
Winkel außerhalb des Intervalls [0;90°] definieren. Wir bewegen uns gegen den Uhrzeigersinn auf dem Einheitskreis und betrachten zunächst im
Quadrant II Winkel w mit 90 ≤ w ≤ 180°. Der Winkel t ist dabei der Ergänzungswinkel zu w bis 180° (bzw. π ) , es gilt also w+t = 180° bzw. w+t = π Die Sinuswerte und Kosinuswerte von t sind schon definiert und die Werte für w kann man wie im Bild unten gezeigt direkt daraus ablesen: sin(w) = sin(180°t) = sin(t) und cos(w) = cos(180°t) =  cos(t). Zum Beispiel ist sin(135°) = sin(180°  45°) = sin(45°) = 2 1/2 und cos(135°) = cos(180°45°) =  cos(45°) =  2 1/2 . Die Werte für die Ausdehnung in die verbleibenden Quadranten III (180° ≤ w ≤ 270°) und IV ( 270° ≤ w ≤ 360° ) ergeben sich analog durch Spiegelung
an der xAchse. Alle Informationen dazu im Bild unten, Vorzeichen beachten. Zahlenbeispiele: sin(190°) = sin(180° + 10° ) =  sin(10°). cos(243°) = cos(180°+ 63°) =  cos(63°). sin(333°) = sin(360°  27°) = sin(27°). cos(359°) = cos(360°1°) = cos(1°). Im Bogenmaß: sin(11 π /12 ) = sin(π  π /12) = sin(π /12) und cos(17π /14) = cos( π + 3π /14) =  cos(3π) Wir sehen also: Alle Werte der Sinus und
Kosinusfunktion aus dem Intervall [0;90°] (bzw. [0;π/2] wiederholen sich in den anderen Quadranten bis auf das Vorzeichen.
Konstruktion des Sinusgraphen aus den Werten im Einheitskres. Mit der DesmosOnlineDemo Für Winkel w > 360° (bzw 2 π ) sowie Winkel w < 0 drehen wir einfach weiter am Rad sprich dem Einheitskreis und sehen so, dass sich alle Werte der
Sinus und der Kosinusfunktion wiederholen. Nach 360° (2 π ) sind wir wieder am Ausgangspunkt. sin(t+ 360° ) = sin(t) cos(t+ 360° ) = cos(t) sin(t+ 2π) = sin(t) cos(t+ 2π) = cos(t) sin(t+ k 360° ) = sin(t) cos(t+ k 360° ) = cos(t) für alle ganzen Zahlen k. sin(t+ k 2π) = sin(t) cos(t+ k 2π) = cos(t) für alle ganzen Zahlen k. Die Sinus und Kosinusfunktion lässt sich damit auf die ganze reelle Achse 2 π periodisch (360°periodisch) ausdehnen! Jeder Wert lässt sich
auf einen Wert für einen Winkel im Intervall [0;90°] bzw. [0;π/2] zurückführen. Es genügt also, diese Werte zu kennen (Tabellen)! Eigenschaften der Trigonometrischen Funktionen Maximaler Definitionsbereich von Sinus und Kosinus wie oben dargestellt ℝ. Am Einheitskreis kann man ablesen: Wertemenge: [1;1]. Die Funktionen sind 2π periodisch: Für alle x ∈ ℝ und alle ganzen Zahlen k gilt: sin(x + 2k π ) = sin(x) und cos(x + 2k π ) = cos(x) Der Kosinus ist ein um π /2 verschobener Sinus: Für alle x ∈ ℝ gilt die Gleichung: cos(x) = sin(x + π /2) = sin(x π /2) Umkehrfunktion arctan() Symmetrie : arctan() und der Hauptwert des tan sind punktsymmetrisch bezgl Nullpunkt, also ungerade Funktionen.
Die allgemeine Sinusfunktion x → f(x) = a sin(bx+c) + d ; x ∈ ℝ |a|>0 heißt Amplitude, |b|>0 Frequenz. Die Änderung dieser Größen spielt zum Beispiel in der Signalübertragung (Rundfunktechnik) eine Rolle: AM und FM. Amplitudenmodulation (AM) Die Wirkung der Parameter a, b, c, d kann hier interaktiv getestet werden : Mit Zeichenumgebung flot verschiedene Param. asin(x) Mit Zeichenumgebung flot/Schieberegler sin(bx) Mit Zeichenumgebung flot/Schieberegler sin(x+c) Mit Zeichenumgebung flot/Schieberegler sin(x) +d Mit Zeichenumgebung flot/Schieberegler a*sin(bx+c) +d Mit Zeichenumgebung flot/Schieberegler Mit Zeichenumgebung rgraph (nicht für IE8!) Interaktiver Graphenplot mit dem Framework flot
2.0
sin(x)
2sin(x)
1.5
sin(2x)
sin(2x+ Pi /3)
1.0
0.5+ sin(2x)
0.5
0.0
0.5
1.0
1.5
2.0
0.0
π/2
π
3π/2
Wähle Graphen der transformierten Sinusfunktionen aus zum Vergleich mit sin(x) , z.B. paarweiser Vergleich. sin(x)
2sin(x)
sin(2x)
sin(2x+ Pi /3)
0.5+ sin(2x)
Erläuterungen:
1. Parameter a: f(x)= asin(x) Wirkung: Streckung/Stauchung des Graphen um |a| in
y. Wenn a<0 dann zugleich Spiegelung an xAchse. Periodenlänge 2 π
2. Parameter b: f(x) = sin(bx) Periodenlänge: 2 π /b Streckung des Graphen um den Faktor 1/|b| in x.
Keine Verschiebung des Graphen auf der xAchse. Gezeichnet wurde: f(x) = sin(x), sowie sin(0.5x) Nullstellen x=0; x= 2 π; x = 4π; ... x=2π... sin(2x)
3. Parameter c: f(x) = sin(x+c) Periodenlänge: 2 π Verschiebung des Graphen um  c auf der xAchse. Erklärung: x+c=0 für x=c. Das Bild zeigt: f(x) = sin(x) h(x) = sin(x π /4 ) (Nullstellen verschoben um π /4 nach rechts!) g(x) = sin(x + π /3 ) (Nullstellen verschoben um π /3 nach links!)
4. Parameter b und c: f(x) = sin(bx+ c ) = sin( b ( x+ c/b) ) Periodenlänge: 2 π /b Streckung des Graphen um 1/|b| in x und dann
Verschiebung um  c/b auf der xAchse. Das Bild zeigt: f(x) = sin(x) also b=c=0 , sowie sin(2x π /3 ) Parameter: b=2, c=1/3 (Verschiebung der Nullstelle x=0 um π /6 = c/b nach
rechts) 5. Parameter d f(x) = d + sin(x ) Verschiebung des Graphen um d auf y Achse. Das Bild zeigt: f(x) = sin(x) also d=0, sowie 0,8 + sin(x) Parameter: d=0,8 Zur allgemeinen Sinusfunktion Symmetrie asin(bx) = asin(bx) (Punktsymmetrie zum Nullpunktungerade Funktion ) acos(bx) = a cos(bx) (Achsensymmetrie bezüglich yAchsegerade Funktion ) Verschiebung der Nullstellen (Bilder oben) und Streckung /Verschiebung des Graphen Vergleiche die Funktion sin(x) mit der Funktion f(x) = sin(bx +c) = sin(b(x+ c/b)). Die Bilder oben zeigen bereits den Zusammenhang an Beispielen. Allgemeine Rechnung zur Nullstellenverschiebung: Nullstellen des Sinus: 0 = sin(0) = sin( π) = sin( 2π)= sin( 3π)=.... Also: 0 = sin( bx +c) für b x + c =0 , für b x + c = π, für b x + c = 2π usw. Lösungen: x 1 = c/b, x 2 = (π c) / b, x 3 = (2π c) / b, usw. Die 1. Nullstelle 0 des Sinus wird also um c/b verschoben. Der Graph wird um den Faktor 1/|b| gestaucht in x Richtung. Der Abstand der Nullstellen beträgt π /b Die Periodenlänge von f beträgt 2π /b (Der Abstand benachbarter Nullstellen beträgt genau die halbe Periodenlänge) Bei der Funktion sin(x) entspricht das Intervall [0; 2π ] gerade dem Intervall [ x 1 ; x 3 ] (für b > 0) bzw. dem Intervall [ x 3 ; x 1 ] (für b < 0 ) bei der
Funktion sin(bx+c). Beispiel: f(x)= sin(2x  π /2 ). b=2 und c =  π /2 x 1 = c/b = π /4 x 2 = (π c) / b = 3π /4 x 3 = (2π c) / b = 5π /4 Periodenlänge: π Im Bild (rot die Intervalle einer Periode. ) : Lösungen von Sinusgleichungen und Umkehrfunktionen : &; Die Gerade y=0,7 schneidet den Graphen der Sinusfunktion zweimal im Intervall I= [0;2π] , ebenso die Gerade y=0,4. Wohingegen die Geraden y=1 und
y=1 den Graphen im Intervall I= [0;2π] jeweils nur einmal berühren. Im Intervall I= [0;2π] (sogar in jedem Intervall der Länge 2π ) hat die Gleichung sin(w) = y (bzw. cos(w)= y ) für jede vorgegebene Zahl y mit 0 < |y| < 1 genau zwei Lösungen w 1 und w 2 . Der Taschenrechner liefert in der Regel nur eine dieser Lösungen. Bei
negativen y in der Regel auch einen negativen Winkel. Der Taschenrechner löst also die Sinusgleichung nur auf im Intervall [π /2 ; π /2 ]. Die zweite Lösung muss man sich über den Einheitskreis oder den Graphen durch Winkelverschiebung verschaffen. Beispiele: 1. sin(w) = 1/2. Taschenrechner/Tabelle: w 1 = sin 1 (1/2) = π /6. Die zweite Lösung im Intervall I ist w 2 = π  π /6 = 5π /6. 2. sin(w) = 1/2. Taschenrechner/Tabelle: w 1 = sin 1 (1/2) = π /6. Die zweite Lösung ist π + π/6 = 5 π / 6. Umkehrfunktion des Sinus Damit ist auch klar, dass die
Umkehrfunktion arcsin(x) , D = [1;1] (auf Taschenrechnern
auch oft sin 1 bezeichnet) jeweils immer nur zu einer
Sinusfunktion eingeschränkt auf eines der Intervalle [π /2 +kπ ; π /2 + kπ ]; (k aus Z) existieren kann. Im Bild eine Darstellung des Hauptwerts
arcsin(). Die angegebenen Werte stimmen allerdings nicht 
es müsste ja arcsin(1) = π /2 sein! Die anderen Werte erhält
man wie oben demonstriert durch Verschiebung um
geeignete Winkel  siehe Einheitskreis oder Sinusgraph. Für den Kosinus erhält man jeweils auf Intervallen [kπ ; π kπ ]; (k ganze Zahl) eine Umkehrfunktion arccos(x)
D=[1;1] . Lösung allgemeiner Sinusgleichungen. Gegeben y mit |y| ≤ 1. Gesucht x mit a sin(bx+c) + d = y. Voraussetzung |a| > 0. und |b| > 0
1. Die Gleichung ist äquivalent zu sin(bx+c) = (yd)/b 2. Substitution w = bx +c 3. Löse sin(w) = (yd)/a wie oben beschrieben. Wenn |(yd)/a| < 1 dann gibt es zwei Lösungen w 1 und w 2 , aber für |(yd)/a| = 1 nur eine Lösung 4. Alle Lösungen auf der reellen Achse bekommt man durch die 2π Periodizität. Eine Lösung der Ausgangsgleichung hat stets die Darstellung w 1 (k) = w 1 + k 2π oder w 2 (k) = w 2 + k 2π mit einer ganzen Zahl k. 5. Auflösen der Substitution: bx+ c = w(k) also x = ( w(k)  c )/ b. Die Lösungsmenge ist also x 1 (k) = (w 1 + k 2π  c) / b und x 2 (k) = (w 2 + k 2π  c) / b Wenn die Lösung auf einem bestimmten Intervall gesucht wird, dann muss man die Zahlen k passend auswählen, dass Lösungen im Intervall liegen. Beipiel 1: Nullstellenbestimmung (y=d ) Bestimme die Lösungsmenge der Gleichung 4sin( 5x + π/4) = 0. 1. Die Gleichung ist offenbar äquivalent zu sin( 5x + π /4) = 0 2. Substitution: w = 5x + π /4 . 3. Die Gleichung sin(w) = 0 hat im Intervall [0, 2π [ die Lösungen w 1 = 0 und w 2 = π (Auf dem abgeschlossenen Intervall [0, 2π ] gäbe es noch die Lösung w=2π , aber die erhalten wir ohnehin aus w 1 über die 2π Periodizität.) 4. Somit sind alle Lösungen auf der reellen Achse gegeben durch w(k) = 0 + 2kπ und w(k) = π + 2kπ mit ganzen Zahlen k. 5. Auflösen der Substitution: x 1 (k) = ( 0 + 2kπ  π /4) / 5 = ( (8k1)π ) / 20 x 2 (k) = ( π + 2kπ + π /4 . ) / 5 = ( (8k+3) π/4 ) / 5 = ( (8k+3) π/20 ) k=0: ( π ) / 20 k=1: (7/20)π und (8+3)π ) / 20 = (11/20)π usw. Beispiel 2. Bestimme die Lösungsmenge der Gleichung 5sin(2x + π /4) = 5. 1. Die Gleichung ist offenbar äquivalent zu sin( 2x + π /4) = 1 2. Substitution: w = 2x + π /4 . 3. Die Gleichung sin(w) = 1 hat im Intervall [0, 2π ] die Lösung w 1 = π /2 4. Somit sind alle Lösungen auf der reellen Achse gegeben durch w(k) = π /2 + 2kπ mit ganzen Zahlen k. 5. Auflösen der Substitution: x(k) = (π /2 + 2kπ  π /4) / 2 = ( π /4 + 2kπ )/2 = π /8 + kπ k=0: x(0)= π /8 ; k=1: x(1) = (9/8) π usw. ... k=1: x(1) = π /8  π k=2: x(2) = π /8  2π = (15/8) π /8 + kπ usw. Beispiel 3. Bestimme die Lösungsmenge der Gleichung 2sin(3x + π /2) +1 = 2 . 1. Die Gleichung ist äquivalent zu sin( 3x + π /2) = 1/2 2. Substitution w = 3x + π /2 . 3. Die Gleichung sin(w) = 1/2 hat im Intervall [0, 2π ] die Lösungen w 1 = π /4 und w 2 = 3π /4. 4. Somit sind alle Lösungen auf der reellen Achse gegeben durch w(k) = π /4 + 2kπ und w(k) = 3π /4 + 2kπ mit ganzen Zahlen k. 5. Auflösen der Substitution: x 1 (k) = (π /4 + 2kπ  π /2) / 3 = ( π /4 + 2kπ ) / 3 =  π /12 + 2kπ/3 x 2 (k) = (3π /4 + 2kπ  π /2) / 3 = ( π /4 + 2kπ ) / 3 = π /12 + 2kπ/3 Wenn wir zum Beispiel alle Lösungen x im Intervall [0; 3π ] suchen, dann müssen wir die Zahlen k passend wählen. 0 ≤ x 1 (k)=  π /12 + 2kπ/3 ≤ 4 π für k=1; k=2; k=3; k=4. 0 ≤ x 2 (k) π /12 + 2kπ/3 ≤ 4 π für k=0; k=1; k=2; k=3; k=4. Im Intervall lägen also die 9 Lösungen x 1 (1) =  π /12 + 2π/3 ; ... x 1 (4) =  π /12 + 8π/3 und x 2 (0)= π /12 + 2kπ/3 ... x 2 (4)= π /12 + 8π/3. Differentialrechnung mit trigonometrischen Funktionen Die Sinus und Kosinusfunktionen bilden ein "geschlossenes System" bezüglich der Differentiation. f(x) = sin(x) f'(x) = cos(x) f''(x) =  sin(x) f'''(x) = cos(x) f''''(x) = f(x) g(x) = cos (x) g'(x) = sin(x) g''(x) =  cos(x) g'''(x) = sin(x) g''''(x) = g(x) Die Sinusfunktion eignet sich damit zur Beschreibung von Vorgängen, bei denen die 2. Ableitung oder die 4. Ableitung des Zustands proportional zum
Zustand sind, z.B. Schwingungen. (siehe Expeditionen/Schwingungen) Die Bestimmung von Extremalstellen führt direkt wieder auf die oben behandelte Nullstellenbestimmung bei trigonometrischen Funktionen. Beispiel: Gesucht sind die Extremalstellen der Funktion f(x) = 2 sin(3x + π /4). Wir bestimmen als Kandidaten dafür zunächst die Nullstellen der Ableitung. Kettenregel beachten. Bestimme also die Lösungsmenge von f'(x) = 6 cos(3x + π /4) = 0. Das Problem ist durch π /2 Verschiebung aber äquivalent zum Problem 6 sin( 3x + π /4 + π /2) = 6 sin( 3x + 3π /4 ) =0. Nun bestimmen wir nach dem Schema von Beispiel 1 die Nullstellen. Die Zahlen k sind dabei immer ganze Zahlen. 3 x(k) + 3π /4 = 0 + 2k π oder 3 x(k) + 3π /4 = π + 2k π Dies liefert die Lösungsmenge x 1 (k) = ( 3π /4 + 2k π ) /3 oder x 2(k) = ( π /4 + 2k π )/3 Einsetzen der Zahlen in die 2. Ableitung f''(x) = 18 sin(3x + π /4) : f''( x 1 (k) ) = 18 sin( ( 3 π /4 + 2k π ) + π /4) = 18 sin(  π /2 + 2k π) = 18 > 0 f''(x 2 (k) ) = 18 sin( ( π /4 + 2k π ) + π /4) = 18 sin( π /2 + 2k π) = 18 < 0 Die Zahlen x 1 (k) sind also die lokalen Minimalstellen von f auf der ganzen reellen Achse, die Zahlen x 2 (k) die lokalen Maximalstellen. Sie sind auch globale, da der Funktionswert an diesen Stellen 2 bzw. +2 beträgt und wegen 2|sin()| ≤ 2 auch
nicht kleiner bzw. größer werden kann.