Bewegte Ladungen im Magnetfeld
Werbung
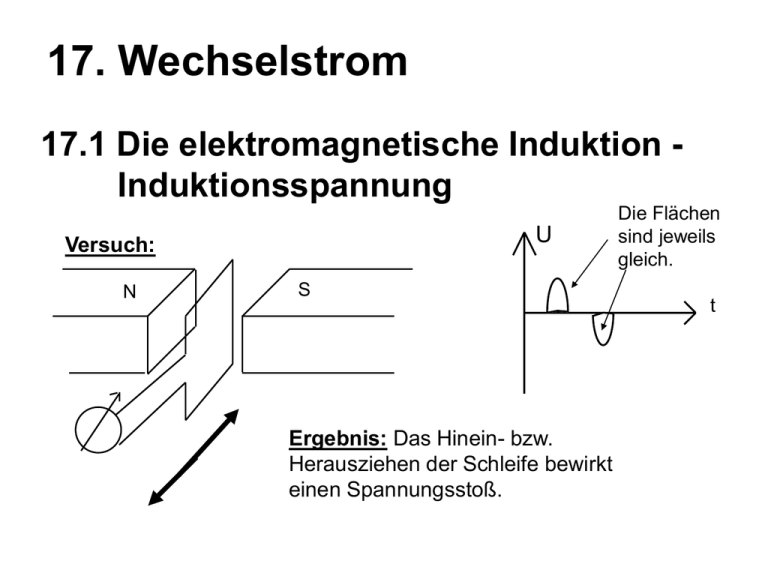
17. Wechselstrom 17.1 Die elektromagnetische Induktion Induktionsspannung U Versuch: N S Ergebnis: Das Hinein- bzw. Herausziehen der Schleife bewirkt einen Spannungsstoß. Die Flächen sind jeweils gleich. t Versuch 2: Wird die Schleifenebene parallel zu den Kraftlinien hineingeschoben, wird keine Spannung induziert. Bei Drehen der Schleife Spannungsstoß. Dieser Vorgang heißt elektromagnetische Induktion, die dabei hervorgerufene Spannung Induktionsspannung. Es fließt ein Induktionsstrom. Die Induktion wurde 1831 durch Michael Faraday entdeckt. Seit 1870 werden nach diesem Prinzip Generatoren gebaut. Generatoren sind Wandler von Energie: Mechan. Energie in elektr. Energie Eine Spannung wird induziert, wenn • sich ein Leiter in einem Magnetfeld bewegt, • sich der magnetische Fluss durch die Schleife ändert. (m = B·A) Entstehung der Induktionsspannung: Auf jeden Ladungsträger wirkt eine Lorentz-Kraft. S + FL = qvB v N - Es kommt zu einer Verschiebung der Elektronen im Leiter, bis es zu einem Gleichgewicht kommt. Es bildet sich nämlich ein elektrisches Feld. Fel = qE elektrische Kraft E ... elektrische Feldstärke q ... el. Ladung Gleichgewichtszustand: FL + Fel = 0 qvB + qE = 0 E = -vB ·l El = -vBl Uind = -vBl Induzierte Spannung an den Leiterenden. Berechne: Hufeisenmagnet: B=0,01T; l=10cm = 0,1m; v = 1m/s. Ergebnis: Uind = - 1.0,01.0,1 = -0,001V = -1 mV Der bewegte Leiter wird durch eine Schleife ergänzt. B Fm I v ds Wir verschieben den Leiter um ds, das bewirkt eine Induktionsspannung, die einen Induktionsstrom zu Folge hat. l Deshalb wirkt auf den Leiter eine Lorentzkraft, die die Bewegung hemmt. Um sie aufrechtzuerhalten müssen wir Arbeit verrichten. Dies ist in Einklang mit dem Energieprinzip. Lenzsche Regel: Der Induktionsstrom ist stets so gerichtet, dass er seiner Ursache entgegenwirkt. Bewegen des Leiters um ds: Dies führt zu einer Änderung des magnetischen Flusses m dm = B.dA = B.l.ds = B l.v.dt = -Uind.dt d U ind dt d dt In einer Leiterschleife induzierte Spannung. ... Änderung des magnetischen Flusses d U ind N dt Induktionsgesetz allgemein N ... Anzahl der Windungen Versuch: V Öffnen des Schalters in I I II Das Induktionsgesetz ist allgemein gültig: dA UindN B dt dB Uind N A dt d Uind N dt Bewegung, bzw. Fläche ändert sich Die magn. Flussdichte ändert sich. Spannungsstoß in II Schließen des Schalters in I Versuche zur Lenzschen Regel: Ergebnis: Beim Einschalten wird der Ring abgestoßen, beim Ausschalten wir der angezogen. Beim Einschalten wirkt das Magnetfeld des Rings schwächend auf das Magnetfeld der Spule, beim Ausschalten verstärkend. (Der Zusammenbruch des Magnetfeldes soll verhindert werden.) Versuchsvariation: Thomsonsche Kanone (Beachte: Verwende dazu Wechselstrom ca. 60-70V) 17.1.1 Anwendungen der Induktion: Erarbeite die Anwendungen aus dem Buch (BW 7) S. 54 Magnettonabnehmer Schreib-Leseköpfe für Magnetspeicher INDUSI (Induktive Zugsicherung) (Folie) FI-Schalter (Siehe Abb. 54.3) FI-Schalter 17.1.2 Wirbelströme Versuch: Bei Bewegung eines massiven leitenden Körpers in einem Magnetfeld treten Wirbelströme auf. Nach der Lenzschen Regel sind sie so gerichtet, dass die darauf wirkende Lorentzkraft die Bewegung hemmt. Anwendung: Wirbelstrombremse in E-Motoren. Zusatzbremse bei LKWs Unangenehme Eigenschaft der Wirbelströme: Starke Erwärmung. Bei Eisenkernen von Elektromagneten würde dies zur Schwächung des Magneten führen. Daher Lamellierung des Eisenkerns. Weiterer Versuch zu Wirbelstrom: Durch Kupferrohr und durch Plastikrohr gleicher Länge wird ein Magnet frei fallen gelassen. Begründe! 17.2 Die Selbstinduktion Um eine Glimmlampe zum Leuchten zu bringen ist eine Zündspannung von ca. 170 V erforderlich. (Zeigen!!!) Versuch: 17.2 Die Selbstinduktion Um eine Glimmlampe zum Leuchten zu bringen ist eine Zündspannung von ca. 170 V erforderlich. (Zeigen!!!) Versuch: Ergebnis: Beim Einschalten leuchtet die Lampe nicht, beim Ausschalten schon. Die Änderung des Spulenstroms bewirkt eine Induktionsspannung. d Uind N dt in allen N Windungen Kraftflussdichte im Innern einer Spule: NI B 0 l B A Wir setzen ins Induktionsgesetz ein: UN d NI (0 A) dt l A LN 0 l 2 N20 A dI l dt L ... Induktivität der Spule dI UL L dt Selbstinduktionsspannung in einer Spule. Sie wird durch die Änderung der Stromstärke in einer Spule hervorgerufen. Die Einheit der Induktivität heißt 1 Henry (1H) Ein Henry tritt auf, wenn eine gleichmäßige Änderung des Stromes um 1 Ampere pro Sekunde eine Spannung von 1 Volt hervorruft. Beim Ausschalten tritt eine besonders hohe Selbstinduktionsspannung auf, da dort die Änderung von I besonders stark ist. Rechenbeispiel: A12 S 67 (BW 3) 1,256 106 6002 0,012 L 1,42 103 H 0,1 3 U L 1,42 10 10 0,0142 V 17.2.1 Die magnetische Energie Im magnetischen Feld kann Energie gespeichert werden. (vgl. Versuch mit Glimmlampe) Die Spule mit der Induktivität L wird mit einer Gleichspannungsquelle U gespeist. U dI UL L dt L Die Selbstinduktionsspannung ist der Klemmenspannung entgegengesetzt. 2. KH. R. U + UL = 0 UL dI dt → U = - UL Die elektrische Arbeit, die zum Aufbau des magnetischen Feldes aus der Spannungsquelle in der Zeit dt abgegeben wird, entspricht dem Produkt aus der elektrischen Leistung mal der Zeit dt. W = P·dt = U·I·dt Die elektrische Arbeit entspricht dem Energiebetrag dE, um den sich die magnetische Feldenergie vergrößert. dE = U·I·dt dEL Wir setzen für U ein: dI I dt dt dEL I dI L I2 Emagn. L I dI 2 Beweis: d L I2 2LI ( ) LI dt 2 2 Vgl. Abb. 68.1 L.I L I Emagn. 2 2 I I Die magnetische Feldenergie entspricht der Fläche unter dem Graphen. 17.3 Der Wechselstromgenerator Mit Kohlebürsten greift man an den Schleifringen die elektrische Spannung ab. B n = B.A.cos = BAcost ... zwischen der Normale auf die Leiterschleife und den magnetischen Feldlinien = 0 cos = 1 Fluss am größten d d Uind N N (BA cos t)NBA sin t dt dt UindU0 sin t Spannung beim Wechselstromgenerator Bei Anschließen eines Verbrauchers fließt ein sinusförmiger Wechselstrom. V B W n U I F Die Kraft, die auf den Leiter wirkt hemmt die Bewegung. Zur Aufrechterhaltung ist Arbeit nötig. Diese Arbeit wird vom Generator in elektr. Energie umgewandelt. Technische Ausführung: Innenpolmaschine (Feldmagnet innen) Die Induktionsspulen sind im Stator (verlustfreierer Abgriff). An Bürsten würden sich starke Funken bilden. 17.4 Der Gleichstromgenerator Anstelle der beiden Schleifringe verwendet man einen Kommutator. Dieser polt nach einer Umdrehung von 180° die Stromrichtung um. 17.4 Der Gleichstromgenerator Der Kommutator polt nach einer Umdrehung von 180° die Stromrichtung um. Damit fließt der Strom immer in dieselbe Richtung. Wir erhalten einen pulsierenden Gleichstrom. U pulsierender Gleichstrom N S U ind U 0 sin t t Verwendet man mehrere gegeneinander versetzte Spulen und statt des Kommutators einen Kollektor, erhält man einen "glätteren" Gleichstrom. Dynamoelektrisches Prinzip von Siemens 1867: Anstelle des Permanentmagneten wird ein Elektromagnet verwendet. Dieser wird vom Generator selbst gespeist. Die Remanenz des Eisenkerns bewirkt bei der ersten Umdrehung eine kleine Induktionsspannung, die einen Induktionsstrom zur Folge hat. Dieser baut das Feld weiter auf, ... bis zur Sättigung. Gleichstromgeneratoren werden verwendet um die Feldspulen der Wechselstromgeneratoren zu speisen, als Lichtmaschine in Fahrzeugen usw. 17.5 Widerstände im Wechselstromkreis Versuch: Ergebnis: Die Glühlampe vor der Induktivität leuchtet später. Grund: Selbstinduktion hat einen Strom, der dem Strom aus der Batterie entgegengesetzt ist. Erst wenn das Magnetfeld aufgebaut ist, leuchtet die Lampe. Variante: Rasches Aus- und Einschalten: Glühlampe hinter L leuchtet überhaupt nicht mehr. Folgerung: Der induktive Widerstand wird bei höherer Frequenz größer. 17.5.1 Ohmscher Widerstand im Wechselstromkreis U ~ I I und U sind konphas. R U0 I U( t ) U 0 sin t U 0 sin t I( t ) I0 sin t R 0 t Leistung im Wechselstromkreis bei rein ohmschem Verbraucher: Diese wird im ohmschen Widerstand wie beim Gleichstrom in Wärme umgewandelt. Leistung im Wechselstromkreis bei rein ohmschem Verbraucher. Diese wird im ohmschen Widerstand wie beim Gleichstrom in Wärme umgewandelt. P(t) = U(t).I(t) = U0.I0.sin2t Die Leistung schwankt periodisch. U, I, P Leistung beim Wechselstrom 4 3 2 1 0 -1 0 -2 -3 1 2 3 4 5 6 Zeit Spannung Stromstärke Leistung 7 Die Momentanleistung ist nicht interessant. Wir errechnen den zeitlichen Mittelwert. Die Fläche unter der Kurve ist die Arbeit während einer Periode. W P T Es gilt: T = 2 T T 0 0 T W P(t) dt U0 I0 sin t dtU0 I0 sin2 t dtU0 I0 2 0 T 2 1 T 1 T sin 2T0 Es gilt nämlich: sin t dt (1 cos 2t)dt 2 4 2 0 02 T 2 T 0 T T 0 0 W P(t) dt U0 I0 sin2 ωt dt T U0 I0 sin 2 ωt dt 0 Fläche unter der Kurve bis T ist die Arbeit in einer Periode. 2π T 1 2 2 sin ( ω t ) dt sin u du 0 ω 0 Bei der Substitution ändern sich auch die Grenzen: t = 0 u = 0 2π T 2π t = T u = ω∙T = T uωt du ωdt 2π 2π 1 1 2 π 2 2 sin u du cosu sinu 0 ( cos u) du ω 0 ω 0 partielle Integration: f sinu F cosu g sinu g cosu 2π 2π 2 π 1 1 2 2 sin u du cos u sin u ( 1 sin u) du 0 ω 0 ω 0 0 2π 2π 2π 1 1 1 2 2 sin u du 1 du sin u du ω 0 ω 0 ω 0 2π 2 1 2π 2 sin u du u0 ω 0 ω 2 ω 2π 2π 0 sin u du ω 2 Wir substituieren wieder zurück: u ωt du ω dt Auch die Grenzen: unten 0; oben T T 2 2π 2 sin ( ω t ) dt ω :2 ω0 ω T 2 sin (ωt) dt 0 π π T ω 2 π 2π 2 ω T T Wir erhalten also als Arbeit in einer Periode T: T T T T W P(t) dt U0 I0 sin t dtU0 I0 sin t dtU0 I0 2 0 0 0 2 2 T U0 I0 U0 I0 U0 I0 W 2 P Ueff Ieff T T 2 2 2 Ueff Ieff Ueff, Ieff sind die Effektivwerte von Spannung und Stromstärke. Ein Gleichstrom mit den Effektivwerten würde dieselbe Leistung erbringen. Bei der Angabe der Spannung einer Wechselstromsteckdose gibt man stets die Effektivwerte an. U Auch mit Messgeräten misst man meist die Effektivwerte. 325 230 t Ein Oszillograph kann die Scheitelwerte messen. Bei induktiven und kapazitiven Widerständen kommt es zu einer Phasenverschiebung. Außerdem sind diese Widerstände frequenzabhängig. Die Leistung bei verschiedenen Widerständen errechnet sich daher folgendermaßen: Wirkleistung: 1 P U0 I0 cos Ueff Ieff cos 2 cos ..... Leistungsfaktor Ueff.Ieff ..... Scheinleistung Die Wirkleistung wird in Watt (W) angegeben, die Scheinleistung in VoltAmpere (VA). In Wechselstromkreisen tritt daher immer ein Blindstrom auf, der zu Energieverlusten (Erwärmung der Leitungen) führt. Diese Blindströme belasten das Stromnetz und sind daher unerwünscht.











