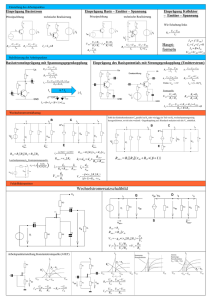
Formelsammlung Bauelemente und Grundschaltungen 1

Formelsammlung Baugruppen
1
1.1
RCL-Schaltungen
Kondensator
Das Ersatzschaltbild eines Kondensators C besteht aus einem Widerstand R p parallel zu C, einem Serienwiderstand Rs und einer Induktivität Ls in Reihe zu Rp
und C.
Allgemeines
C
=
² 0 · ²r ·
XC
=
1
ωC
A
d
(1)
(2)
Verlustwinkel δ des Kondensators (Serieninduktivität Ls = 0)
tanδ
=
Pw
Pb
(3)
tanδ
=
1
+ ω · Rs · C
ω · Rp · C
(4)
Für f ≈ 1 kHz gilt:
tanδ
≈
1
ω · Rp · C
(5)
tanδ
≈
ω · Rs · C
(6)
Pw
Pb
Wirkleistung
Blindleistung
Für f À 1 kHz gilt:
1.2
Induktivität
Die Spule wird durch ein Ersatzschaltbild beschrieben, das aus einer idealen Induktivität L und einem Verlustwiderstand Rv zu ihr in reihe beschrieben wird. Rv
setzt sich folgendermaßen zusammen: Kupferverluste (∼ ω), Wirbelstromverluste
(∼ ω 2 ), Hystereseverluste (∼ ω).
Allgemeines
AL
=
AR
=
Rcu
=
L
XL
Am
lm
ωAL
Q
N 2 ∗ AR
µ·
Am
= N 2 · µ0 · µr ·
= N 2 · AL
lm
= ωL
1
(7)
(8)
(9)
(10)
(11)
Verlustwinkel δ der Induktivität
tanδ
=
Rv
Pw
=
Pb
ω·L
(12)
Spulengüte Q
Q
=
Qmax
=
1
tanδ
AL
ω·
AR
(13)
(14)
Resonanzfrequenz
1
√
2π L · C
fr =
2
(15)
Allgemeines zu Leitern
NL · γ
Ar
ρ = nA · e
S = ρQ · µ · E
S
σ =
= ρQ · µ
E
1
% =
σ
nA
nA
S
ρ
e
NL
γ
Ar
σ
%
3
=
Atomdichte
Stromdichte
Ladungsträgerdichte
Elementarladung e = 1.6 · 10−19 As
Avogadro-Konstante NL = 6 · 1023 Atome
mol
g
Spezifische Dichte [γ] = cm
3
g
Relative Atommasse [Ar ] = mol
Spezifischer Leitwert
Spezifischer Widerstand
Halbleiter
3.1
Allgemeines
Herstellung von pn-Übergängen
1. Legierungsverfahren
2. Diffusionsverfahren
3. Epitaxialverfahren
4. Ionen-Implantationsverfahren
2
(16)
(17)
(18)
(19)
(20)
Grundsätzliche Zusammenhänge
WB
ni = N0 · e− 2KT
n·p
µp,n
ni
n
p
N0
WB
k
T
kT
=
n2i
(21)
(22)
Löcher- bzw. Elektronen-beweglichkeit
Eigenleitungsdichte
Elektronendichte
Löcherdichte
Zustandsdichte, stoff- und schwach temperaturabhängig
Energiebetrag zum Aufbrechen einer Valenzbrücke =¿ Bandabstand
Boltzmann-Konstante = 1.38 · 10−23 Ws/k
absolute Temperatur
mittlere thermische Energie eines Elektrons
Der Bandabstand WB bei Zimmertemperatur beträgt ca. k · T0 = 0.026eV
3.2
Leitfähigkeit reiner Halbleiter
σ
µp,n
ni
3.3
=
e · ni · (µn + µp )
(23)
(24)
Löcher- bzw. Elektronen-beweglichkeit
Eigenleitungsdichte
Leitfähigkeit dotierter Halbleiter
N-Dotiert
Aus der N-Dotierung resultiert, daß nn À pn , nn À ni und nn = ND .
n n · pn
=
pn
=
σn
=
n2i
n2i
nn
(25)
(26)
e · N D · µn + e ·
n2i
· µp
ND
(27)
P-Dotiert
Aus der P-Dotierung resultiert, daß pp À np , pp À ni und pp = NA .
µp,n
ni
nn
pp
σ
ND
NA
pp · n p
=
np
=
σn
=
n2i
(28)
n2i
(29)
pp
e · N A · µp + e ·
n2i
· µn
NA
Löcher- bzw. Elektronen-beweglichkeit
Eigenleitungsdichte
Elektronendichte
Löcherdichte
Spezifischer Leitwert
Donatordichte (Anzahl der Fremdatome pro Volumen)
Akzeptordichte (Anzahl der Fremdatome pro Volumen)
3
(30)
3.4
P-N Übergang
Raumladungsdichten
p-Seite: e · NA
n-Seite: e · ND
Diffusionsspannung
UD
=
UT · ln
µ
¶
NA · N D
n2i
(31)
Flußspannung
UF
=
m · UT · ln
µ
IF
IS
¶
(32)
Diffusionsströme
Idiff,p
Idiff,n
U
UT
A
k
µp,n
Ln,p
NA,D
=
=
A · k · T · µp ·
A · k · T · µn ·
n2i
ND
³
n2i
NA
³
U
e UT − 1
Lp
U
´
(33)
´
(34)
e UT − 1
Ln
externe Spannung über dem p-n-Übergang
Temperaturspannung (25.9mV bei 300K) UT = k·T
e
Querschnitt
Boltzmannkonstante
Elektronen- bzw. Löcherbeweglichkeit
Diffusionslänge der Elektronen bzw. Löcher
Akzeptor- bzw. Donatordichte der p- bzw n-Seite
Majoritäts- und Minoritätsladungsträgerstrom
Imaj
Imin
=
=
A · e · N{A,D} · E · µ{p,n}
(35)
A·e·
(36)
n2i
N{A,D}
· E · µ{n,p}
Diodenstrom (Shockleygleichung)
U
IS
UT
m
ID
=
IF
=
³ U
´
I S · e UT − 1
´
³ U
IS · e m·UT − 1
externe Spannung über dem p-n-Übergang
Sättigungsstrom
Temperaturspannung (25.9mV bei 300K) UT =
siehe Text
4
(37)
(38)
k·T
e
Der Faktor m berücksichtigt, ob Ladungsträger nur außerhalb der Sperrschicht
(m = 1) oder, bei sehr kleinen und sehr großen Flußströmen, auch innerhalb der
Sperrschicht (m = 2) rekombinieren.
Differentieller Widerstand
rD
=
UT
ID
(39)
Bei der idealen Diode würde der diffentielle Widerstand bei steigendem Diodenstrom immer weiter abnehmen. Bei realen Dioden strebt er einem Grenzwert, dem
Bahnwiderstand, zu.
Diffusionskapazität
CD
Tp,N
3.5
Tp + T N
2 · UT
=
(40)
Lebensdauer der Minoritätsladungsträger
auf der p- bzw. n-Seite, bis sie rekombinieren. Typ.: 0.1ns ... 1ms
Verhalten des P-N Übergangs im Sperrbereich
Sperrschichtweite
WS
WS
UR
²
²0
²r
=
s
2·²
· UR ·
e
µ
1
1
+
NA
ND
¶
(41)
Sperrschichtweite
Sperrspannung
² = ² 0 · ²r
Dielektrizitätskonstante: 8.85 pf/m
Si:12; Ge:16
Sperrschichtkapazität
CS
=
CS
=
CS
UR
A
²·A
⇒
WS
r
²·A
³
2 · UR · e² · N1A +
(42)
(43)
1
ND
Sperrschichtkapazität
Sperrspannung
Querschnitt
5
´
4
Zweiweg Gleichrichter
Verlustleistung der Dioden (idealisiert mit Knickkennlinie)
Pvges
Pvges
UF 0
rF
IF
IF eff
2
2 · UF 0 · IF + 2 · rF · IF2 eff
=
(44)
Gesamte Verlustleistung der Dioden
Durchbruchspannung der idealisierten Diode
Bahnwiderstand der Diode
Mittelwert des Diodenstroms
Effektivwert des Diodenstroms
Anzahl der Dioden im Strompfad (hier Grätzschaltung)
Welligkeit
W
5
5.1
π
2 3 · RL · C · 2πf
√
≈
(45)
Transistor
Bipolortransistor
Wenn nicht anders vermerkt, beziehen sich alle Angaben auf den NPN - Bipolartransistor.
Kleinsignalersatzgrößen (Bild: Skript 4-8)
rBE
=
S
=
rCE
=
B
UT
IC0
IC0
UT
UA
IC0
(46)
(47)
(48)
Arbeitspunktberechnung (Bild: Skript 4-25 untenrechts)
IC = B ·
UB · R2 − UBE (R1 + R2 )
RE · (B + 1)(R1 + R2 ) + R1 · R2
(49)
Kenngrößen der Emitterschaltung
Spannungsverstärkung ohne Emitterkondensator:
Vu
≈
RC
RE
(50)
Spannungsverstärkung mit Emitterkondensator (Emitter wechselspannungsmäßig
an Masse):
Vu
≈
−S(rCE ||RC )
6
(51)
Eingangswiderstand:
Ze
=
R1 ||R2 ||rBE
(52)
(53)
rCE ||RC
(54)
Ausgangswiderstand:
Za
=
(55)
Temperaturabhänigkeit des Arbeitspunktes
∆UBE
5.2
≈
−2mV/K · ∆T
(56)
Feldeffekttransistor (FET)
Der FET verhält sich bis zu einer gewissen Drain-Source-Spannung fast wie ein
ohmscher Widerstand, dessen Wert sich mit der Gate-Source-Spannung einstellen
läßt. D. h. mit steigender DS Spannung steigt auch der Strom (ID ) durch den
Transistor. Ab einer gewissen DS Grenzspannung (Abschnürgrenze UGS = UDS )
bleibt der Strom konstant. Oberhalb der Abschnürgrenze läßt sich der Strom des
Transistors mit der GS Spannung einstellen.
UGT ist die Gate-Schwellen-Spannung.
Verlauf der Abschnürgrenze
2
K/2 · UDS
(57)
2
)
K · ((UGS − UGT ) · UDS − 1/2 · UDS
(58)
IDp
=
Ohmscher Bereich
ID
=
Oberhalb der Abschnürgrenze (UDS ≥ UGS − UGT , UGS ≥ UGT )
ID
=
K/2 · (UGS − UGT )2
(59)
Steilheit der Übertragungskennlinie (ID = f (UGS ))
Gilt nur für den Abschnürbereich, also: (UDS ≥ UGS − UGT , UGS ≥ UGT )
S
=
K · (UGS − UGT )
7
(60)