Elektromagnetische Wellen

Elektromagnetische Wellen
Kapitel 16
Elektromagnetische
Wellen
+
+
+
+
+
+
+
+
+
+
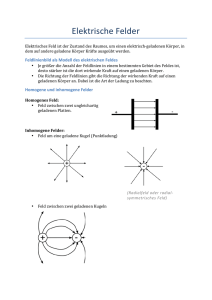
Das radiale elektrische Feld, das von einem unendlich langen,
geraden, positiv geladenen Draht erzeugt wird.
Figur 1.
Wir nehmen nun an, dass die positiven Ladungen zur Zeit t=0 anfangen, sich mit einer Geschwindigkeit VD zu bewegen. Zur Zeit t=t1
hält der Draht wieder an. D.h. der Draht bewegt sich während des
Zeitintervalls zwischen t=0 und t=t1 in Richtung des Drahts.
16.1 Felder eines bewegten geladenen
Drahtes
Wir haben in Kap. 15.5.1 das elektrische Feld berechnet, das von
einem unendlich langen, geladenen Stab erzeugt wird. Das Feld ist
radial und hängt umgekehrt proportional vom Abstand r des Stabes
ab:
r
2l 1
( unendlicher Stab)
E ª
4pe 0 r
Wie wird die räumliche Verteilung des elektrischen Feldes sein?
Die elektrischen Feldlinien müssen den Ladungen folgen. Sie
müssen immer bei den positiven Ladungen beginnen. Aber
das Feld kann sich nicht gleichzeitig und spontan in allen
Punkten des Raumes ändern!
Die Relativitätstheorie sagt voraus, dass die Information über die
Bewegung des Drahtes sich nicht schneller als mit Lichtgeschwindigkeit ausbreiten kann.
wobei l die Linienladungsdichte ist.
Wir betrachten einen positiv geladenen Stab. Das erzeugte elektrische
Feld ist in Abb. 1 gezeigt.
Physik
991
Wir nehmen deshalb an, dass die Änderung des Feldes sich mit einer
Geschwindigkeit v durch den Raum ausbreitet, wobei die
Geschwindigkeit v später bestimmt wird.
992
Physik I&II, WS 02/03-SS03, Prof. A. Rubbia (ETH/Zürich)
Felder eines bewegten geladenen Drahtes
Elektromagnetische Wellen
Es folgt daraus, dass das Verhalten des elektrischen Feldes wie in
Abb. 2 gezeigt ist.
E+ und E– der Drähte werden sich kompensieren und das resultierende elektrostatische Feld verschwindet in jedem Punkt des Raumes.
Die Ausbreitung der Änderung des Feldes verhält sich wie ein Puls,
der sich mit einer Geschwindigkeit v bewegt:
Der positiv geladene Draht bewegt sich nun mit der Geschwindigkeit
VD zwischen den Zeiten t=0 und t=t1. Der negativ geladene Draht
ruht.
1.
2.
3.
In den Punkten mit Abständen grösser als vt entsprechen die elektrischen Feldlinien noch dem Draht, bevor er sich bewegte.
Zwischen den Abständen vt und v(t-t1) ändern sich die Feldlinien.
Die elektrischen Felder der einzelnen Drähte sind in Abb. 3 gezeigt.
Ein Puls, der von der Bewegung der positiven Ladungen erzeugt
wird, wird sich ausbreiten.
Für Abstände kleiner als v(t-t1) entsprechen die Feldlinien der
neuen Position des Drahtes.
+
+
+
+
+
+
t>0 +
+
+
+
vt
VD
t > t1
+
+
+
+
+
+
+
+
+
+
–
–
–
–
–
–
–
–
–
–
v(t–t1)
vt
Der positiv geladene Draht bewegt sich zwischen der Zeit t=0 und
t=t1 in Richtung des Drahts. Ein Puls, der sich mit einer Geschwindigkeit v
ausbreitet, wird erzeugt.
Figur 2.
Die elektrischen Felder zweier geladener, paralleler Drähte. Der
positiv geladene Draht bewegt sich während des Zeitintervalls t=0 und t=t1.
Figur 3.
Wir nehmen nun eine Anordnung an, in der zwei Drähte sich nebeneinander befinden. Einer ist positiv geladen und der andere ist mit
derselben Ladung, aber negativ geladen. Die elektrostatischen Felder
Physik
993
+
+
+
+
+
+
+
+
+
+
994
Physik I&II, WS 02/03-SS03, Prof. A. Rubbia (ETH/Zürich)
Felder eines bewegten geladenen Drahtes
Elektromagnetische Wellen
Das resultierende elektrische Feld ist die Vektorsumme der elektrischen Felder der positiv, respektive negativ geladenen Drähte:
r r
r
E = E+ + E-
Nach den Maxwellschen Gleichungen gilt
r
r r
∂
∂
∂E
= e 0m 0 ( E x , E y , E z ) = e 0m 0 (0, 0, E z )
— ¥ B = e 0m 0
∂t
∂t
∂t
Es verschwindet in jedem Punkt des Raumes ausserhalb des Pulses.
wobei wir die z-Koordinate entlang des Drahtes angenommen haben.
Siehe Abb. 4.
Es folgt,
r r Ê ∂B ∂By ˆ r Ê ∂Bz ∂B ˆ r Ê ∂By ∂B ˆ r
- x ˜ ey + Á
- x ˜ ez
—¥ B = Á z ˜e - Á
∂z ¯
Ë ∂x
∂y ¯
Ë ∂y
∂z ¯ x Ë ∂x
–
+
= e 0m 0
E–
E+
E–
∂
(0, 0, E z )
∂t
v
E
E+
E+
Wir bemerken, dass die x- und y-Komponenten der Rotation des Feldes verschwinden. Wir nehmen an, dass die x- und y-Komponenten
des Feldes unabhängig von der z-Koordinate sind, weil wir den Draht
entlang der z-Koordinate angenommen haben. Das Problem ist deshalb entlang der z-Koordinate symmetrisch:
E
E–
∂Bx ∂By
=
=0
∂z
∂z
Das resultierende Feld. Die elektrischen Felder, die von den
positiven und negativen Ladungen erzeugt werden, kompensieren einander
in jedem Punkt des Raumes ausserhalb des Pulses, der sich mit der
Geschwindigkeit v bewegt.
Figur 4.
fi x und y - Komponente
unabhängig von z - Koordinate
Daraus folgt:
Es folgt daraus, dass
∂Bz ∂Bz
=
=0
∂x
∂y
ein Strom, der während einem Zeitintervall nach oben gerichtet fliesst, ein nach unten gerichtetes elektrisches Feld erzeugt.
Das elektrische Feld verhält sich wie ein “Puls”, der sich mit
einer Geschwindigkeit v radial ausbreitet.
fi z - Komponente
unabhängig von x, y - Koordinaten
Natürlich wissen wir aus der Elektrodynamik, dass ein sich veränderndes elektrisches Feld ein magnetisches Feld erzeugt.
Wie muss sich in diesem Fall das magnetische Feld verhalten?
Physik
995
996
Physik I&II, WS 02/03-SS03, Prof. A. Rubbia (ETH/Zürich)
Felder eines bewegten geladenen Drahtes
Elektromagnetische Wellen
Die z-Komponente des Feldes ist unabhängig von x und y, d.h. vom
Abstand r. Weil wir erwarten, dass sie nach Null geht, wenn r nach
unendlich geht, muss sie überall verschwinden:
B
Bz = 0
Eine Lösung, die diese Bedingungen erfüllt, hat die Feldlinien des
magnetischen Feldes in konzentrischen Kreisen um den Draht:
r
Ê y x ˆ
B( x, y, z, t) = B0 ( x, y, t)Á - , , 0˜
Ë r r ¯
v
v
wobei B0 eine Funktion ist, die bestimmt werden muss.
v
v
Siehe Abb. 5.
Wir haben mit dieser Herleitung das folgende erhalten:
Ein elektromagnetischer Puls, der einen elektrischen und
einen magnetischen Teil enthält, wird erzeugt, wenn ein Strom
während eines kurzen Zeitintervalls durch einen geraden
Leiter fliesst. Der elektromagnetische Puls breitet sich mit
einer Geschwindigkeit v radial aus.
E
Elektromagnetischer Puls, der erzeugt wird, wenn ein Strom
während eines kurzen Zeitintervalls durch den geraden Leiter fliesst. Der
Puls breitet sich mit der Geschwindigkeit v radial aus.
Figur 5.
Die elektrischen und magnetischen Felder zeigen senkrecht
zur Ausbreitungsrichtung des Pulses .
Um die Beziehung zwischen den Feldern zu bestimmen, betrachten
wir ein Linienintegral des magnetischen Feldes für einen Puls.
Es gilt,
r
r r
∂E
— ¥ B = e 0m 0
∂t
Siehe Abb. 6.
Physik
997
E
998
fi
r
r
r
r r
ÚÚ (— ¥ B) ◊ dA = Ú B.dr = e m
0
A
C
Physik I&II, WS 02/03-SS03, Prof. A. Rubbia (ETH/Zürich)
0
r r
d
E ◊ dA
ÚÚ
dt A
Felder eines bewegten geladenen Drahtes
Elektromagnetische Wellen
Wir bemerken, dass
r r
r r
∂
Ú B.dr = Bh = e 0m0 ∂t ÚÚ E .dA =
C
A
B
= e 0m 0
v
wobei v die Ausbreitungsgeschwindigkeit des Pulses ist.
Es folgt, dass die Beträge der Felder nur von der Feldkonstanten und
der Ausbreitungsgeschwindigkeit abhängen:
Integrationskurve
h
∂
dr
( Ehr) = e 0m 0 Eh = e 0m 0 Ehv
∂t
dt
r
r Ê
1 ˆ r Êvˆ r
B = (e 0m 0v ) E = Áe 0
2 v˜ E = Á 2 ˜ E
Ëc ¯
e
Ë
¯
0c
r
Wir bemerken, dass der Betrag des magnetischen Feldes um den Faktor v/c2 kleiner ist, als der Betrag des elektrischen Feldes.
E geht in die
v Blattebene hinein
16.2 Die elektromagnetischen Wellen
Die Maxwellschen Gleichungen sagen die Existenz der elektromagnetischen Wellen voraus. Maxwell hat im Jahr 1865 diese Existenz
vorhergesagt.
Hertz1 hat erst 20 Jahre später einen experimentellen Nachweis der
elektromagnetischen Wellen erbracht.
Integrationskurve für die Bestimmung des magnetischen Feldes.
Das elektrische Feld geht in die Blattebene hinein. Der elektromagnetische
Puls breitet sich mit der Geschwindigkeit v aus.
Figur 6.
Im Allgemeinen werden elektromagnetische Wellen erzeugt,
wenn geladene Teilchen beschleunigt werden.
1. H. Hertz (1857-1894).
Physik
999
1000
Physik I&II, WS 02/03-SS03, Prof. A. Rubbia (ETH/Zürich)
Elektromagnetische Wellen
Die elektromagnetischen Wellen
16.2.1 Die Wellengleichung und die
Ausbreitungsgeschwindigkeit
r
r
Ï r Ê r rˆ Ê r r ˆ r
∂2 E
∂ r r
∂Ê
∂E ˆ
—
¥
=
—
—
◊
E
—
◊
—
E
=
B
=
e
m
e
m
Ô Á {˜ Á {
0 0
˜
∂t 2
∂t
∂t ÁË 0 0 ∂t ˜¯
Ô Ë = 0 ¯ Ë —r 2 ¯
r
Ì
∂2B
∂ r r
Ô r Ê r rˆ Ê r r ˆ
—
—
◊
—
◊
—
=
E
—
¥
e
m
=
e
m
B
B
Á
˜
{
{
0
0
0
0
Á r ˜
Ô Ë
∂t 2
∂t
Ë —2 ¯
=0 ¯
Ó
(
Wir beginnen mit den Maxwellschen Gleichungen im Vakuum (d.h.
die Ladungsdichte r=0 und die Stromdichte j=0)
r
Ïr r
∂B
Ô— ¥ E = Ô
∂t
r
Ì
∂E
Ôr r
—
¥
B
=
e
m
0 0
ÔÓ
∂t
Wir bilden die Rotation der beiden Gleichungen:
r
r ∂B
Ïr r r
∂ r r
= - —¥ B
Ô— ¥ — ¥ E = -— ¥
Ô
∂t
∂t
r
Ì
r ∂E
∂ r r
Ôr r r
ÔÓ— ¥ — ¥ B = e 0m 0— ¥ ∂t = e 0m 0 ∂t — ¥ E
(
(
Diese vektoriellen Gleichungen entsprechen einem System von 6
Gleichungen, eine für jede Komponente der Felder
r
∂ 2x 1 ∂ 2x
∂ 2x ∂ 2x ∂ 2x
— 2x = 2 + 2 + 2 = e 0m 0 2 ∫ 2 2
∂t
∂z
∂y
∂x
v ∂t
)
wobei x(x,y,z,t)=Ex, Ey, Ez, Bx, By, und Bz.
Nun benutzen wir eine mathematische Beziehung für ein beliebiges
Vektorfeld F:
r
r r
r r r
r r r
— ¥ — ¥ F = — —◊ F - —◊— F
(
) (
) (
)
oder die Wellengleichungen der elektromagnetischen Wellen
r
r
r2 r
r2r
∂2B
∂2 E
— B = e 0m 0 2
und
— E = e 0m 0 2
∂t
∂t
)
(
)
Im Kap. 15.1.2 haben wir die magnetische Feldkonstante so definiert:
)
m0 ∫
1
e 0c 2
wobei der Laplace-Operator (eine Skalargrösse) gegeben ist durch
r r r
∂2
∂2
∂2
— ◊ — = —2 = 2 + 2 + 2
∂z
∂y
∂x
Die Ausbreitungsgeschwindigkeit der Wellen, die der Wellengleichung folgt, ist daher gleich
Laplace - Operator
v2 =
Es folgt,
1
= c 2 !!!
e 0m 0
Wir haben bewiesen, dass sich die elektromagnetischen Wellen mit
Lichtgeschwindigkeit ausbreiten.
Physik
1001
1002
Physik I&II, WS 02/03-SS03, Prof. A. Rubbia (ETH/Zürich)
Die elektromagnetischen Wellen
Die Beziehung zwischen den Beträgen der Felder ist die folgende:
r Êvˆ r 1 r
B = Á 2˜ E = E
Ëc ¯
c
oder
r
r
E =cB
für elektromagnetische Wellen
Physik
1003