Selbstinduktion Übersicht

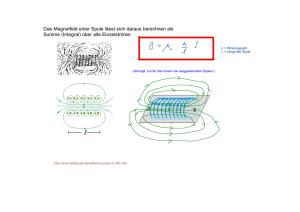
Basiswissen | Skripte
◮ Induktion | Selbstinduktion
Skript
Selbstinduktion
Übersicht
1 Einführung
1
2 Wiederholung
1
2.1 Induktionsgesetz . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.2 Regel von Lenz . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
©
1
1
3 Geradliniger Wurf
1
4 Selbstinduktion
2
5 Induktivität L
3
6 Energie im Magnetfeld
4
Karlsruhe 2014 | SchulLV | Laura Schnepf
Vervielfältigung nur innerhalb einer Lehrer-/Klassen- oder Schullizenz und mit Hinweis auf PhysikLV erlaubt.
www.PhysikLV.net
Basiswissen | Skripte
◮ Induktion | Selbstinduktion
Skript
1 Einführung
Wird ein Stromkreis, in dem eine Spule und eine Glühbirne in
Reihe geschalten sind, geschlossen, so fließt ein Strom.
Beobachtet man die Helligkeit der Glühlampe während des Einschaltvorgangs, fällt auf, dass die Lampe erst verspätet zu
leuchten beginnt und nur langsam ihre maximale Helligkeit erreicht. Auch beim Ausschalten leuchtet die Birne noch eine Zeit
lang, obwohl der Stromfluss schon vorher unterbrochen wurde.
Dieses Phänomen kann man sich mit dem Induktionsgesetz
und der Lenzschen Regel erklären.
2 Wiederholung
2.1 Induktionsgesetz
Du hast bereits gelernt, dass eine Spannung Und induziert wird, wenn sich die vom Magnetfeld durchsetzte Fläche A oder das Magnetfeld B um einen Leiter ändert. Zur Bestimmung
der induzierten Spannung wird das sogenannte Induktionsgesetz verwendet:
Und = −N ·
Δ
Δt
N entspricht dabei der Windungszahl der Induktionsspule, Δt ist die vergangene Zeit und
Δ die Änderung des Magnetischen Flusses.
2.2 Regel von Lenz
Bei der Induktion einer Spannung durch die Änderung des Magnetischen Flusses gilt folgende Regel:
Der Induktionsstrom ist stets so gerichtet,
dass er die Ursache seiner Entstehung zu
hemmen versucht.
Ausführlichere Erklärungen zum Induktionsgesetz und zur Lenzschen Regel findest du im
PhysikLV-Skript „Induktion“.
3 Geradliniger Wurf
Im Skript „Induktion“ haben wir folgenden Versuchsaufbau betrachtet: In einem Leiterstab
oder in einer Spule mit N Windungen wird eine Spannung induziert, indem der Stab bzw.
die Spule in einem Magnetfeld bewegt oder das Magnetfeld verändert wurde.
Das Magnetfeld wurde durch einen Dauermagneten erzeugt.
©
Karlsruhe 2014 | SchulLV | Laura Schnepf
Seite 1/4
Vervielfältigung nur innerhalb einer Lehrer-/Klassen- oder Schullizenz und mit Hinweis auf PhysikLV erlaubt.
www.PhysikLV.net
Basiswissen | Skripte
◮ Induktion | Selbstinduktion
Skript
Nun verwenden wir zur Erzeugung des magnetischen Feldes anstatt des Dauermagneten
eine so genannte Feldspule. Dies ist eine Spule, die – wie der Name bereits sagt – das magnetisches Feld erzeugt, welches für die Induktion einer Spannung nötig ist.
Das magnetische Feld der Spule entsteht folgendermaßen:
Um jeden stromdurchflossenen Leiter verlaufen die
sogenannten magnetischen Feldlinien. Die Rich-
e-
Richtung des
Magnetfelds
+
Elektronenfluss
tung dieser Feldlinien kannst du mit der „LinkenFaust-Regel“ bestimmen. Der Daumen zeigt dabei in die Richtung des Elektronenflusses, also vom
Minus- zum Pluspol! Die gekrümmten restlichen
-
Finger deuten in die Richtung der Feldlinien.
Eine Spule besteht aus vielen einzelnen aufgewickelten
Leitern, um die jeweils Feldlinien verlaufen.
Die Summe der magnetischen Feldlinien um jeden einzelnen dieser Leiter ergibt das magnetische Feld der gesamten Spule.
Feldlinien durch einen Spulenquerschnitt
Quelle: wikimedia.org – Geek3 (CC-BY-SA-3.0).
4 Selbstinduktion
L
R
Nun betrachten wir einen Stromkreis, in dem ein
Widerstand und eine Spule in Reihe geschalten
sind. Es wird die Spannung U0 angelegt.
Wird der Schalter geschlossen, fließt ein Strom
A
S
durch den Schaltkreis.
U0
Schließt man den Stromkreis, kann man am Strommessgerät ablesen, dass die Stromstärke
beim Einschalten erst langsam auf den Endewert m ansteigt.
Auch beim Ausschalten fällt auf, dass der Strom eine gewisse Zeit „nachfließt“.
Dieses Versuchsergebnis kannst du dir so erklären: Im Skript „Induktion“ hast du gelernt,
dass die Spannung Und induziert wird, wenn sich die vom Magnetfeld durchsetzte Fläche
oder das Magnetfeld ändern. Dies passiert auch in der Spule. Bevor der Stromkreis geschlossen wird, fließt kein Strom durch die Spule, also wird sie auch von keinem Magnetfeld
umgeben; durch das Schließen des Stromkreises, fließt ein Strom und es baut sich ein Magnetfeld um die Spule auf.
Da der Magnetische Fluss Δ als Δ = A·ΔB definiert ist, bedeutet eine Magnetfeldänderung
gleichzeitig eine Änderung des Magnetischen Flusses.
©
Karlsruhe 2014 | SchulLV | Laura Schnepf
Seite 2/4
Vervielfältigung nur innerhalb einer Lehrer-/Klassen- oder Schullizenz und mit Hinweis auf PhysikLV erlaubt.
www.PhysikLV.net
Basiswissen | Skripte
◮ Induktion | Selbstinduktion
Skript
Diese Änderung des Magnetischen Flusses Δ bewirkt nach dem Induktionsgesetz
die Induktion der Spannung Und . Der Induktionsstrom ist
Δ
nach der Regel von Lenz so gerichtet, dass er seiner UrsaUnd = −N ·
che, also dem Anstieg der Stromstärke im Schaltkreis, entΔt
gegenwirkt.
Die Induktion einer Spannung in einer Spule durch die Änderung
des eigenen Magnetfeldes nennt man Selbstinduktion, Eigeninduktion bzw. Induktivität L!
5 Induktivität L
Um einen linearen Zusammenhang zwischen der in der Spule induzierten Spannung Und
und der Änderung der Stromstärke  anzugeben, wird eine neue physikalische Größe, die
Induktivität L eingeführt:
L=−
⇒
Und
̇(t)
̇ =
d
dt
= momentane Änderung der Stromstärke
Und = −L · ̇(t)
Durch das Schließen des Stromkreises und die Änderung des Magnetfelds in der Spule wird
also die Spannung Und = −L · ̇(t) induziert.
Die gesamte Spannung im Stromkreis setzt sich zusammen aus der angelegten Spannung
U0 und der induzierten Spannung Und :
Uges = U0 + Und = U0 − L · ̇(t)
U
Stellst du die Beziehung R =  ges nach der Stromstärke um und setzt die zuvor aufgestellte
ges
Beziehung für Uges ein, erhältst du folgende Gleichung für die Stromstärke innerhalb des
Stromkreises:
Uges
Uges
U0 − L · ̇(t)
R=
⇒ ges =
=
ges
R
R
Stellst du diese Beziehung nach der Größe ̇(t) um, erhältst du
̇(t) =
U0 − (t) · R
L
.
Mit dieser Gleichung kannst du nun den Verlauf Kurve der gemessenen Stromstärke nachvollziehen:
̇(t) stellt in der Abbildung die Änderung der
Stromstärke, also die Steigung des Graphen
dar.

 m
Zu Beginn ist die Stromstärke gering, also gilt
(t) · R < U0 .
Je größer die Stromstärke wird, desto mehr
nähert sich die Differenz im Zähler der obigen
Gleichung dem Wert 0. Strebt der Zähler gegen den Wert 0, strebt der ganze Bruch, also
die Änderung der Stromstärke gegen 0.
©
Karlsruhe 2014 | SchulLV | Laura Schnepf
Seite 3/4
Vervielfältigung nur innerhalb einer Lehrer-/Klassen- oder Schullizenz und mit Hinweis auf PhysikLV erlaubt.
t
www.PhysikLV.net
Basiswissen | Skripte
◮ Induktion | Selbstinduktion
Skript
6 Energie im Magnetfeld
Die Energie in einem Magnetfeld wird durch folgende Formel beschrieben:
E=
1
2
L · 2
L ist dabei die Induktivität der Feldspule,  die Stromstärke, die durch die Spule fließt.
Diese Energie wird im Magnetfeld der Spule gespeichert.
Auffällig ist die Analogie zur elektrischen Energie eines Kondensators, an dem die Spannung
U anliegt und die mit der Formel
E=
1
2
C · U2
berechnet wird. Auch die elektrische Energie wird im Feld des Kondensators, allerdings nicht
im magnetischen, sondern im elektrischen Feld, gespeichert.
©
Karlsruhe 2014 | SchulLV | Laura Schnepf
Seite 4/4
Vervielfältigung nur innerhalb einer Lehrer-/Klassen- oder Schullizenz und mit Hinweis auf PhysikLV erlaubt.
www.PhysikLV.net