1. Schulaufgabe aus der Physik Lösung

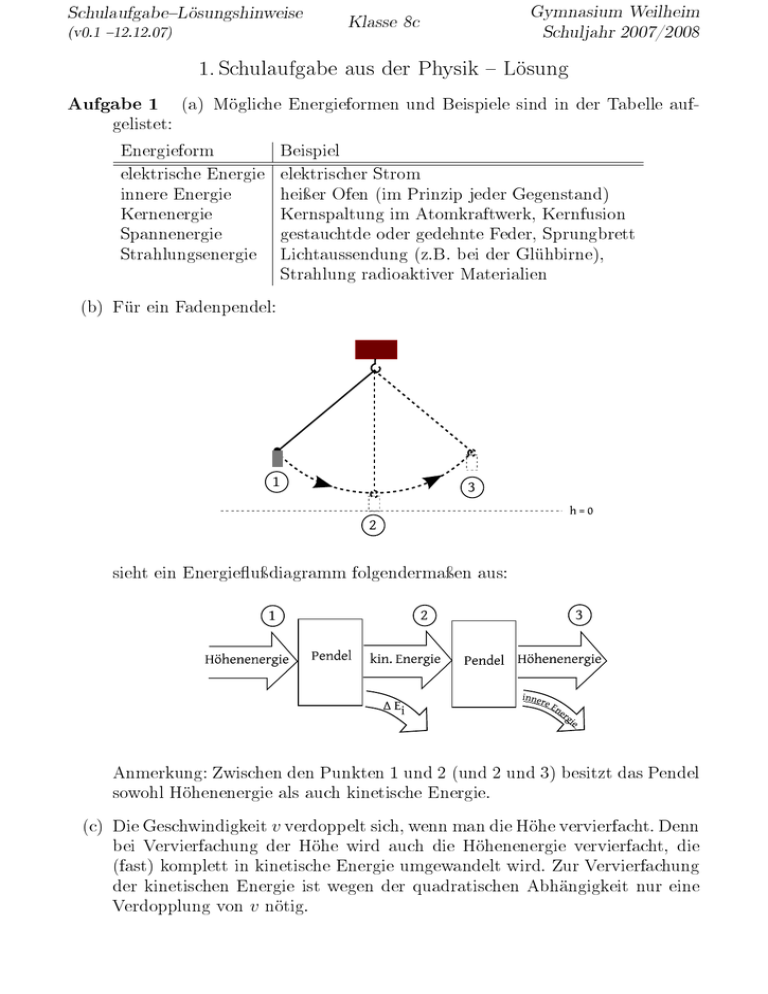
SchulaufgabeLösungshinweise
(v0.1 12.12.07)
Klasse 8c
Gymnasium Weilheim
Schuljahr 2007/2008
1. Schulaufgabe aus der Physik Lösung
Aufgabe 1 (a) Mögliche Energieformen und Beispiele sind in der Tabelle aufgelistet:
Energieform
Beispiel
elektrische Energie elektrischer Strom
innere Energie
heiÿer Ofen (im Prinzip jeder Gegenstand)
Kernenergie
Kernspaltung im Atomkraftwerk, Kernfusion
Spannenergie
gestauchtde oder gedehnte Feder, Sprungbrett
Strahlungsenergie Lichtaussendung (z.B. bei der Glühbirne),
Strahlung radioaktiver Materialien
(b) Für ein Fadenpendel:
sieht ein Energieuÿdiagramm folgendermaÿen aus:
Anmerkung: Zwischen den Punkten 1 und 2 (und 2 und 3) besitzt das Pendel
sowohl Höhenenergie als auch kinetische Energie.
(c) Die Geschwindigkeit v verdoppelt sich, wenn man die Höhe vervierfacht. Denn
bei Vervierfachung der Höhe wird auch die Höhenenergie vervierfacht, die
(fast) komplett in kinetische Energie umgewandelt wird. Zur Vervierfachung
der kinetischen Energie ist wegen der quadratischen Abhängigkeit nur eine
Verdopplung von v nötig.
SchulaufgabeLösungshinweise
(v0.1 12.12.07)
Aufgabe 2
Gymnasium Weilheim
Schuljahr 2007/2008
Klasse 8c
(a) Die kinetische Energie beträgt:
Ekin
1
1
= · m · v 2 = · 75 kg ·
2
2
≈ 14, 2 kJ
70 m
3, 6 s
2
= 14178, 24074 J
(b) Nach dem Energieerhaltungssatz gilt:
E
H,oben
=E
kin, Eintauchen
,
damit folgt:
1
m · g · h = mv 2
2
1
g · h = v2
2
1 v2
h= ·
2 g
2
70
3,6
1
= 19, 2704... m
= ·
2 9, 81 2
≈ 19, 3 m
m
s
m
s
(c) Wieder nach dem Energieerhaltungssatz gilt:
E
H,oben
=E
kin,Eintauchen
und somit auch wieder m · g · h = 12 mv 2 , diesmal muss man nach v auösen:
1
g · h = v2
2
m
m2
v = 2gh = 2 · 9, 81 2 · 15 m = 294, 3 2
s
s
2
und durch Wurzelziehen (Umkehrung zur Quadrierung) erhält man:
v ≈ 17, 2
Aufgabe 3
m
.
s
(a) Nach dem Energieerhaltungssatz gilt:
E
H,höchster Punkt
Und daher:
=E
Spann,maximal
1
m · g · h = D · (∆s)2 ,
2
SchulaufgabeLösungshinweise
(v0.1 12.12.07)
Gymnasium Weilheim
Schuljahr 2007/2008
Klasse 8c
also
1 D · (∆s)2
1 2, 0 · (6, 0 cm)2
1 200 · (0, 06 m)2
h= ·
= ·
= ·
2
m·g
2
60 g · 9, 81 2
2 0, 060 kg · 9, 81
N
N
cm
m
m
N
s
kg
1 200 · 3, 6 · 10−3
= ·
m = 0, 61162... m
2 0, 060 · 9, 81
≈ 0, 61 m.
(b) Die Strecke, um die gestaucht wird, wird verdoppelt. Dadurch vervierfacht
sich die Spannenergie. Diese ist gleich der maximalen kinetischen Energie, also
wird diese auch vervierfacht. Vervierfachung der kinetischen Energie bedeutet
aber eine Verdopplung der Geschwindigkeit.
Man sieht auch direkt aus der Gleichung 12 mv 2 = 21 D(∆s)2 (die man aus dem
Energieerhaltungssatz bekommt), dass v 2 und ∆s2 direkt proportional sind,
also müssen auch v und ∆s direkt proportional sein, und das bedeutet: Eine
Verdopplung von ∆s führt zu einer Verdopplung von v .