1. Schulaufgabe aus der Physik Lösung

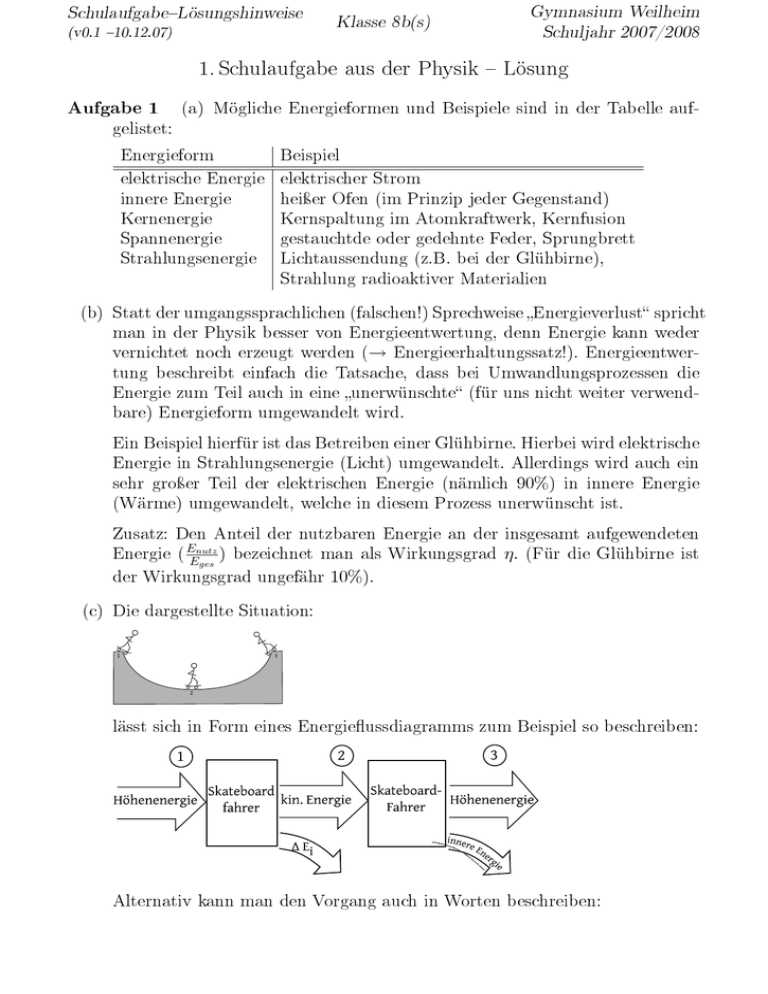
SchulaufgabeLösungshinweise
(v0.1 10.12.07)
Gymnasium Weilheim
Schuljahr 2007/2008
Klasse 8b(s)
1. Schulaufgabe aus der Physik Lösung
Aufgabe 1
(a) Mögliche Energieformen und Beispiele sind in der Tabelle auf-
gelistet:
Energieform
Beispiel
elektrische Energie
elektrischer Strom
innere Energie
heiÿer Ofen (im Prinzip jeder Gegenstand)
Kernenergie
Kernspaltung im Atomkraftwerk, Kernfusion
Spannenergie
gestauchtde oder gedehnte Feder, Sprungbrett
Strahlungsenergie
Lichtaussendung (z.B. bei der Glühbirne),
Strahlung radioaktiver Materialien
(b) Statt der umgangssprachlichen (falschen!) Sprechweise Energieverlust spricht
man in der Physik besser von Energieentwertung, denn Energie kann weder
vernichtet noch erzeugt werden (→ Energieerhaltungssatz!). Energieentwertung beschreibt einfach die Tatsache, dass bei Umwandlungsprozessen die
Energie zum Teil auch in eine unerwünschte (für uns nicht weiter verwendbare) Energieform umgewandelt wird.
Ein Beispiel hierfür ist das Betreiben einer Glühbirne. Hierbei wird elektrische
Energie in Strahlungsenergie (Licht) umgewandelt. Allerdings wird auch ein
sehr groÿer Teil der elektrischen Energie (nämlich 90%) in innere Energie
(Wärme) umgewandelt, welche in diesem Prozess unerwünscht ist.
Zusatz: Den Anteil der nutzbaren Energie an der insgesamt aufgewendeten
Energie (
Enutz
Eges ) bezeichnet man als Wirkungsgrad
η.
(Für die Glühbirne ist
der Wirkungsgrad ungefähr 10%).
(c) Die dargestellte Situation:
lässt sich in Form eines Energieussdiagramms zum Beispiel so beschreiben:
Alternativ kann man den Vorgang auch in Worten beschreiben:
SchulaufgabeLösungshinweise
(v0.1 10.12.07)
Gymnasium Weilheim
Schuljahr 2007/2008
Klasse 8b(s)
Zunächst besitzt der Fahrer im Punkt 1 Höhenenergie. Diese wird beim Herunterfahren in kinetische Energie umgewandelt und in Punkt 2, dem tiefsten
Punkt, besitzt der Fahrer nur noch kinetische Energie. Ein Teil der Höhenenergie wird durch die Reibung in innere Energie umgewandelt.
Beim Hinauahren auf der anderen Seite wird die kinetische Energie wieder
in Höhenenergie umgewandelt, bis im Punkt 3 nur Höhenenergie vorhanden
ist. Auch hier wird ein Teil der (kinetischen) Energie in innere Energie umgewandelt.
Anmerkung: Zwischen den Punkten 1 und 2 (und 2 und 3) besitzt der Fahrer
sowohl Höhenenergie als auch kinetische Energie.
Aufgabe 2
Die Aussage der goldenen Regel der Mechanik lautet: Bei mechani-
schen Vorgängen bleibt das Produkt aus Weg und Kraft (in Wegrichtung) konstant.
Daher gilt: Was man an Kraft spart, muss man an Weg zulegen und umgekehrt.
Für einen Flaschenzug bedeutet das: Durch die Anordnung mit einer (oder mehreren) beweglichen Rolle muss man eine längere Seilstrecke ziehen (für das gezeigte
Bild: die Seilstrecke ist doppelt so lang), daher ist die aufzuwendende Kraft kleiner
(im gezeigten Bild: halb so groÿ aufgrund der doppelten Wegstrecke).
Aufgabe 3
Nach der goldenen Regel der Mechanik gilt:
F G · h = Fs · s
FG die Gewichtskraft des Fasses, h die zu überwindende Höhe (also 50 cm),
Weg, den man zurücklegt, wenn man das Fass rollt (also s = 4 m) und Fs ist
Dabei ist
s
der
die gesuchte Kraft, die man aufwenden muss, um das Fass die Balken hochzurollen.
Die Gewichtskraft
FG
lässt sich berechnen aus der Masse
nämlich
FG = m · g (= 125 kg · 9, 81
N
kg
m und dem Ortsfaktor,
= 1226, 25 N).
SchulaufgabeLösungshinweise
Gymnasium Weilheim
Schuljahr 2007/2008
Klasse 8b(s)
(v0.1 10.12.07)
Also gilt:
m · g · h = s · Fs ,
das heiÿt
1226, 25 N · 0, 5 = 4, 0 m · Fs
und somit
Fs = 1226, 25 N ·
0, 5 m
= 153, 28125 N
4m
≈ 153 N.
Es ist eine Kraft von etwa 153 N notwendig, um das Fass die Balken hinaufzurollen.
Aufgabe 4
Die Höhenenergie
EH
berechnet sich zu
EH = m · g · h,
wobei
m
die Masse des Bergsteigers,
g
der Ortsfaktor und
h
die Höhe über dem
Nullniveau ist. Das Nullniveau ist hier 705 m, die Höhe des Garmischer Bahnhofs.
Also gilt:
EH = 75 kg · 9, 81
N
kg
· (2962 m − 705 m) = 75 kg · 9, 81
N
kg
· 2257 m
= 1660587, 75 Nm
≈ 1661 kJ.
Aufgabe 5
se
m.
(a) Die Höhenenergie ist direkt proportional zu Höhe
und zur Mas-
Eine dreifache Höhe lässt sich also auch durch eine dreifache Masse
ausgleichen um auf den gleichen Betrag der Höhenenergie zu gelangen:
2
EJ = 3 · 1 m · mJens · g = 3 · 9, 81
m
s2
· mJens
2
EJ = 1 m · 3 · mJens · g = 3 · 9, 81
m
s2
· mJens .
(b) Nach dem Energieerhaltungssatz ist die kinetische Energie beim Eintauchen
so groÿ wie die Höhenenergie vor dem Absprung, also
E
kin, Eintauchen
= EH = 735 J.