05.11.2008

Reibungskräfte
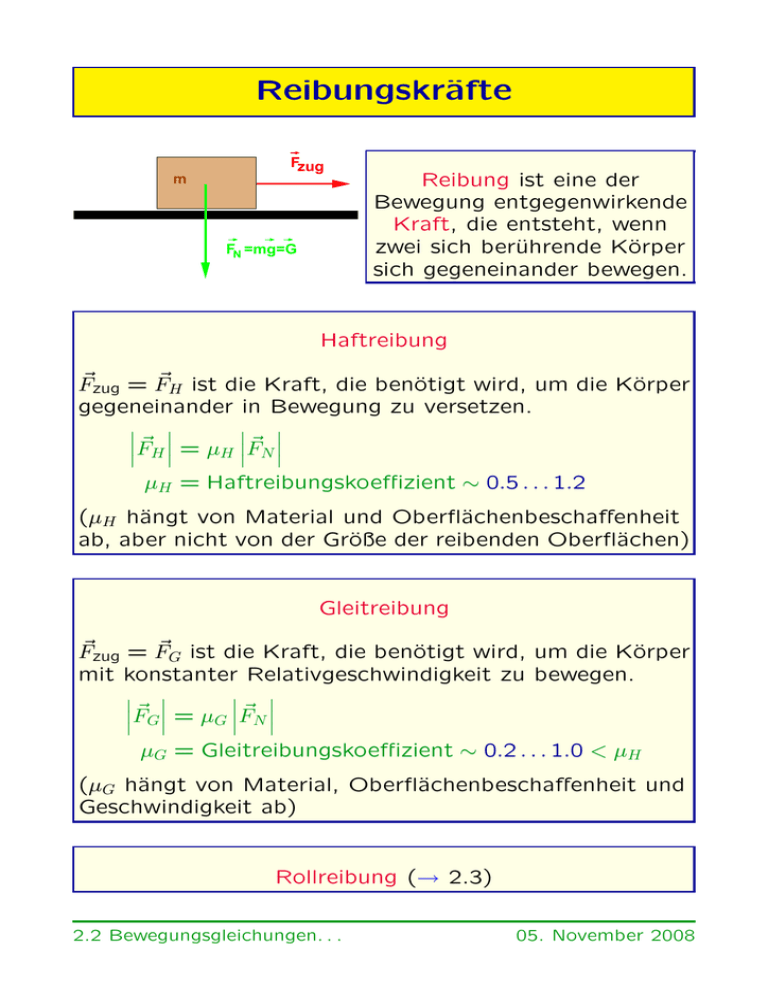
m
Fzug
FN =mg=G
Reibung ist eine der
Bewegung entgegenwirkende
Kraft, die entsteht, wenn
zwei sich berührende Körper
sich gegeneinander bewegen.
Haftreibung
~zug = F
~H ist die Kraft, die benötigt wird, um die Körper
F
gegeneinander in Bewegung zu versetzen.
~ ~ FH = µH F
N
µH = Haftreibungskoeffizient ∼ 0.5 . . . 1.2
(µH hängt von Material und Oberflächenbeschaffenheit
ab, aber nicht von der Größe der reibenden Oberflächen)
Gleitreibung
~zug = F
~G ist die Kraft, die benötigt wird, um die Körper
F
mit konstanter Relativgeschwindigkeit zu bewegen.
~ ~ FG = µG F
N
µG = Gleitreibungskoeffizient ∼ 0.2 . . . 1.0 < µH
(µG hängt von Material, Oberflächenbeschaffenheit und
Geschwindigkeit ab)
Rollreibung (→ 2.3)
2.2 Bewegungsgleichungen. . .
05. November 2008
Kraftfelder
Definition:
Die Kraft, die ein Körper auf einen anderen ausübt,
lässt sich für jeden Punkt im Raum angeben:
~ =F
~ (~
F
r ) = Kraftfeld
(unabhängig davon, ob sich am Punkt ~
r ein Körper
befindet, auf den die Kraft tatsächlich wirkt).
Beispiel: Schwerefeld der Erde
Die Schwerkraft auf einen Körper (Masse m) ist eine
Folge der Gravitationswechselwirkung zwischen
der Erde (Masse ME ) und diesem Körper.
r
mME ~
~ (~
F
r ) = −G
r2 |~
r|
~
r = Ortsvektor von Erdmittelpunkt zu m
~
r/|~
r | = Einheitsvektor in ~
r-Richtung
2
−11 N m
G = Gravitationskonstante = 6.67 · 10
kg2
m
r
Erde, ME
2.2 Bewegungsgleichungen. . .
F
Erdoberfläche:
~ (|~
|F
r | = RE )| = mg
GME
=
m
2
RE
GME
⇒g =
2
RE
⇒ME = 6.0 · 1024 kg
(mit RE = 6.4 · 106 m)
05. November 2008
Das Gravitationsgesetz
Körper mit Masse ziehen sich an:
m1m2 ~
r12
~
F12 = −G
|~
r12|2 |~
r12
m2
F 12
r
Bei ausgedehnten Körpern wirkt die Kraft,
als wäre die Masse jeweils in einem Punkt
(dem sog. Schwerpunkt) vereinigt.
Bei homogenen Kugeln ist
der Schwerpunkt der Mittelpunkt.
12
m1
Messung der Gravitationskonstante:
Gravitationswaage: Gravitations-Anziehung wird durch
Torsionskraft eines Drahtes kompensiert
~G| = 2G
2|F
m1m2
Tφ
=
R2
d
• T = Winkelrichtgröße
• φ = Verdrillung
des Drahtes
Winkeländerung ∆φ
bei Umlegen der
schweren Kugeln:
R2 T ∆φ
G=
4m1 m2 d
2.2 Bewegungsgleichungen. . .
Laser
M
FG
Draht
mit Spiegel
m
m
FG
d
R
M
05. November 2008
Newtonsche Gesetze 1 und 2
Definition:
Impuls = p
~ = m~v
[p] = kg m s−1
Das 1. Newtonsche Gesetz:
Ein Körper, auf den keine Kraft wirkt, verharrt
im Zustand der Ruhe oder der gleichförmigen
Bewegung:
~ =0⇔p
F
~ = const.
Das 2. Newtonsche Gesetz:
Die zeitliche Impulsänderung eines Körpers mit
Masse m wird durch die auf ihn wirkende Kraft
verursacht und ist gegeben durch:
d~
p m=const.
d~v
~
F =
=
m
= m~a
dt
dt
Achtung:
Diese Gesetze gelten nur, wenn das
Bezugssystem unbeschleunigt ist
(d.h. sich mit gleichbleibender
Geschwindigkeit bewegt)
→ Inertialsystem
2.2 Bewegungsgleichungen. . .
05. November 2008
Inertial- und andere Systeme
Scheinkräfte
Betrachte zwei Koordinatensysteme S und S ′:
• S ist Inertialsystem
• S ′ ist beschleunigt
2. Newtonsche Gesetz in S
(m = const.):
¨
′
~ + ~¨
~ = m~
r
F
r¨ = m R
¨
~ − mR
~
⇒ m~r = F
¨′
Beobachter in S ′ erfährt
¨.
~
Scheinkraft −mR
Beispiel: Beobachter in
frei fallendem Fahrstuhl
ist schwerelos
r’
S’
r
R
S
Schwere Masse = träge Masse
• schwere Masse: erzeugt Schwerkraft
• träge Masse: widersetzt sich Beschleunigung
Diese Gleichheit ist nicht selbstverständlich!
Ausgangspunkt für Einsteins allg. Relativitätstheorie:
Beobachter kann Schwerkraft (schwere Masse)
und Beschleunigung (träge Masse) nicht unterscheiden!
2.2 Bewegungsgleichungen. . .
05. November 2008
3. Newtonsches Gestz,
Kraftstoß, Impulserhaltung
Das 3. Newtonsche Gesetz:
Wechselwirken zwei Körper miteinander,
aber nicht mit anderen Körpern, so üben sie
entgegengesetzt gleiche Kräfte aufeinander
aus:
~1 = −F
~2
F
Der Kraftstoß:
Eine über endliche Zeit (von t1 bis t2) einwirkende Kraft
(Kraftstoß) erzeugt eine Impulsänderung:
Zt2
~ (t)dt
F
∆~
p=
(∗)
t1
Impulserhaltung:
Aus (∗) und dem 3. Newtonschen Gesetz folgt für die
Impulsänderung der beiden wechselwirkenden Körper
∆~
p1 = −∆~
p2 ⇒ (~
p1 + p
~2 )|vorher = (~
p1 + p
~2)|nachher
In einem abgeschlossenen System
(keine äußeren Kräfte)
ist die Summe aller Impulse konstant!
2.2 Bewegungsgleichungen. . .
05. November 2008
Die Rakete
Antrieb durch Ausstoß von Treibgas oder Flüssigkeit
wegen Impulserhaltung.
Annahmen: konstante Ausstoßrate dm
=µ
dt
konstante Ausstoßgeschwindigkeit v0
z
p=(m−dm)(v+dv)
p=mv
p=dm(v−vo )
t
t+dt
Impulsänderung in infinitesimalem Zeitintervall dt
p
~ (t) = m~v
p
~ (t + dt) = (m − dm)(~v + d~v ) + dm(~v − ~v0 )
= m~v + m · d~v − dm · ~v0 − |dm{z· d~v}
vernachl.
p
~ (t + dt) − p
~ (t)
d~v
d~
p
!
~ext
=
=m
− µ~v0 = F
dt
dt
dt
=~
0 und ~v (t=0) = ~
0:
⇒
~ext
Für F
µ
µ
d~v
=
~v0 =
~v0
dt
m(t)
m0 − µt
Zt
m0
µ~v0 dt
= [−~v0 ln(m0 − µt)]t0 = ~v0 ln
⇒ ~v (t)=
m0 − µt
m(t)
0
2.2 Bewegungsgleichungen. . .
05. November 2008
Arbeit und Wegintegrale
Arbeit = W =
R
~d
F
[W ] = N m = kg m2 s−2
C
FN
∆s N
Z
~ d~s = lim
F
N
X
|∆~s |→0
N →∞ i=1
C
~i · ∆~si
F
Die ∆~si bilden
einen Polygonzug
entlang dem Weg C.
C
F
1
∆s 1
Beispiele:
Arbeit gegen Schwerefeld beim Heben einer Masse m:
 
 
0
0
~ =  0  = −G
~
d~s =  0  ; F
dz
mg
Zz2
Z
~ d~s = mg dz = mg (z2 − z1)
⇒W = F
| {z }
C
z1
=h
Arbeit gegen Federkraft:
 
 
dx
Dx
~ =  0  = −F
~Rückstell
d~s =  0  ; F
0
0
Zx2
Z
~ d~s = Dx dx = D x2 − x2
⇒W = F
1
2
2
C
2.2 Bewegungsgleichungen. . .
x1
05. November 2008