Entstehung einer Federschwingung - sfz-bw

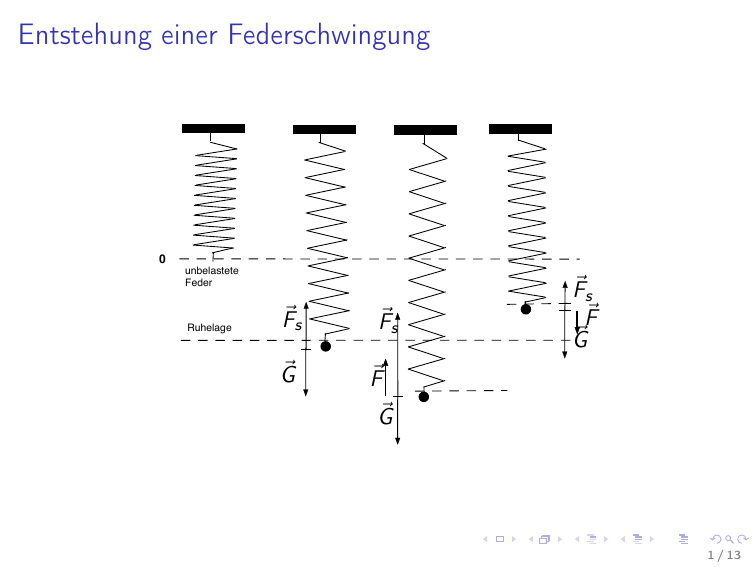
Entstehung einer Federschwingung
!"#$%&'()*+,-./0123456789:;<=>?@ABCDEFGHIJKLMNOPQRSTUVWXYZ[\]^_`abcdefghijklmnopqrstuvwxyz{|}~
0
unbelastete
Feder
Ruhelage
~s
F
~s
F
~
G
~
F
~
G
~s
F
~
F
~
G
1 / 13
Charakteristische Größen
1. Die Schwingungs- oder Periodendauer T ist die Zeit für
einen vollen Hin- und Hergang.
2. Die Frequenz f ist gleich der Anzahl der Schwingungen
je Sekunde
f = nt = T1 .
Einheit [f ] = 1 s −1 = 1 Hz
3. Die momentane Auslenkung oder Elongation s = s(t)
gibt den Weg an, um den sich der schwingende
Massenpunkt aus der Ruhelage entfernt hat.
4. Die Amplitude b
s ist die größte Elongation einer
Schwingung.
2 / 13
Harmonische Schwingung
3 / 13
Gleichförmige Kreisbewegung - harmonische Schwingung
!"#$%&'()*+,-./0123456789:;<=>?@ABCDEFGHIJKLMNOPQRSTUVWXYZ[\]^_`abcdefghijklmnopqrstuvwxyz{|}~
y
s
ω
r
ϕ
s(t)
b
s=r
T
t
Eine mechanische Schwingung, die mit der Projektion einer
gleichförmigen Kreisbewegung übereinstimmt, heißt harmonische
Schwingung.
4 / 13
Geschwindigkeit und Beschleunigung
y
~vt
~r
s,v,a
~vy
~v
~ar ~ay
ωt
~a
ωt
~s
ωt
x
5 / 13
Bewegungsgesetze
Anfangsbedingung t = 0 s, s = 0 m
1. Zeit-Weg-Funktion
s =b
s sin(ω t)
2. Zeit-Geschwindigkeit-Funktion
v = ṡ(t) = ω b
s cos(ω t)
3. Zeit-Beschleunigung-Funktion
s sin(ω t) = −ω 2 s(t)
a = v̇ (t) = s̈(t) = −ω 2 b
6 / 13
Kraftgesetz und Periodendauer
a = −ω 2 s =⇒ F = m a = −m ω 2 s = −D s
q
q
p
D
D
ω
1
2
mω = D ⇒ ω = m ⇒ f = 2π = 2π m
⇒ T = f1 = 2π m
D
Definition
Eine Schwingung ist genau dann harmonisch, wenn sie das lineare
Elongations-Kraftgesetz F = −D s erfüllt.
Die Periodendauer T eines Schwingers der Masse m und der
p
Richtgröße D beträgt T = 2π m
D
7 / 13
Differentialgleichung (DGl) der harmonischen Schwingung
◮
Elongations-Kraftgesetz F = −D s
◮
Newtonsche Grundgleichung:
F = m a =⇒ m a = −D s =⇒ m s̈(t) = −D s(t)
◮
D
DGl zweiter Ordnung: s̈(t) = − m
s(t)
Allgemeine Lösung: s(t) = b
s sin(ω t + ϕ0 ) mit ω =
Anfangsbedingungen: b
s , ϕ0
◮
◮
q
D
m.
s = 0 für t = 0 s ⇒ ϕ0 = 0 ⇒ s(t) = b
s sin(ω t).
π
s =b
s für t = 0 s ⇒ ϕ0 = 2 ⇒
s(t) = b
s sin(ω t + π2 ) = b
s cos(ω t).
8 / 13
Die Energie des harmonischen Oszillators
◮
s 2 sin2 (ω t)
Potentielle Energie: Epot = 12 Ds 2 = 21 Db
◮
◮
Kinetische Energie:
Ekin = 21 mv 2 = 12 mω 2b
s 2 cos2 (ω t) = 12 Db
s 2 cos2 (ω t)
◮
◮
Gleichgewichtslage Epot = 0
Nullage: Ekin maximal; Umkehrpunkt: Ekin = 0
Gesamtenergie: Epot + Ekin = 12 Db
s2
◮
Gesamtenergie proportional zum Quadrat der Amplitude b
s und
zum Quadrat der Frequenz ω = 2πf
9 / 13
Fadenpendel
ϕ
ℓ
◮
Rücktreibende Kraft
Ft = −mg sin(ϕ)
◮
s = ℓϕ ⇒
Kleines ϕ
Ft
s
= − mg
ℓ
sin ϕ
ϕ .
sin ϕ
ϕ ≈1
mg
F
t
◮
s ≈ ℓ
◮
x
~t
ϕ F
~r
F
~
G
s
◮
= D. ⇒
harmonische Schwingung
q
T = 2π gℓ .
10 / 13
Federpendel
0
y0
~s
F
~s
F
~
G
~s
~s
~s
F
~
G
~
F
s<0
0
s>0
~
F
y
~
G
s = y − y0
Rückstellkraft F = −D s.
p
Das Feder-Schwere-Pendel schwingt also harmonisch. T = 2π m
D
11 / 13
Parallel- und Reihenschaltung von Federn
<
=
0
>
1
2
?
3
@
;4
5
6
/7
8
9
:.A
-B
+
,C
*#
D
$
%
)"E
(F
!&
G
'K
JH
L
M
IN
~
O
}P
|m
Q
u
w
v{zyxtR
sln
ko
p
q
rS
T
jU
g
h
V
ià
b
d
ce
W
f_
^]X
\Y
Z
[
s
10
20
D
1
D
1
D
2
s
D
2
D
2
D
1
D
2
D
1
F
F
s
F
Reihenschaltung
s1 + s2 = s ⇒
F
F
1
1
1
F
+
=
⇒
=
+
D1 D2
D
D
D1 D2
Parallelschaltung
F = F1 + F2 ⇒ D · s = D1 · s + D2 · s ⇒ D = D1 + D2
12 / 13
Gedämpfte harmonische Schwingung
!"#$%&'()*+,-./0123456789:;<=>?@ABCDEFGHIJKLMNOPQRSTUVWXYZ[\]^_`abcdefghijklmnopqrstuvwxyz{|}~
13 / 13