8 Mechanische Schwingungen

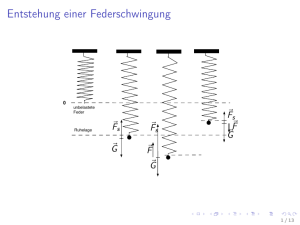
8
Mechanische Schwingungen
Beispiele vorstellen: Federpendel, Fadenpendel, Wassersäule im U-Rohr, Kugel in Rinne,
Maxwell-Rad, Stimmgabel u.s.w
8.1
Grundbegriffe für Schwingungen:
Ruhelage:
ist der Punkt der Bahn, in dem der Körper nach hinreichend langer Zeit bei
schwacher Dämpfung ruhen würde
Umkehrpunkt:
ist ein Punkt der Bahn, in dem die Geschwindigkeit ihre Richtung umkehrt
Periodendauer T:
gibt die Zeit für eine volle Hin- und Herbewegung (Periode) einer
Schwingung an. (bzw.: T = nt mit: t-gesamte Zeit für n Perioden)
[T]=1s
Frequenz f:
gibt die Anzahl der Schwingungen pro Sekunde an (bzw.: f = nt )
[f ] = 1s = 1Hz
es gilt:
f=
1
T
Elongation (momentane Auslenkung) y: gibt den Weg an, um den sich der schwingende
Massenpunkt aus der Ruhelage entfernt hat. Sie ist eine zeitabhängige Größe:
y = y(t)
[ y] = 1m
Amplitude ymax oder ŷ : gibt die größte Elongation an, also die Entfernung zwischen Ruhelage
und Umkehrpunkt. (wichtig: Sie wird immer positiv angegeben.)
Kreisfrequenz ω: ω = 2π ⋅ f (ω bezieht sich auf die zugehörige Kreisbewegung)
Dämpfung:
Eine Schwingung mit konstanter Amplitude heißt ungedämpft. Nimmt die
Amplitude mit der Zeit ab, so heißt die Schwingung gedämpft.
(schwache Dämpfung beim Fadenpendel, starke Dämpfung beim U-Rohr)
1
8.2
Die harmonische Schwingung
Zur Vereinfachung wird zunächst von Reibung abgesehen. Der schwingende Körper wird als
Massenpunkt betrachtet.
Experiment:
Vergleich der Schattenprojektion einer
Kreisbewegung mit dem Schatten eines
Federpendels
Mit dem regulierbaren Motor kann die
Winkelgeschwindigkeit der Scheibe und damit auch des
kleinen Zylinders so eingestellt werden, dass sich die
Schatten des Zylinders und des schwingenden Körpers
synchron bewegen.
⇒
Für beide Schatten gilt die gleiche Zeit-OrtFunktion.
mathematische Beschreibung:
y*
y
t3
t3
t4
t2
ymax
t2 t4
ϕ
t5
y
t1
x*
t1t5
t1
t2
t3
t4
t5
t6
t7
t8
t9
t10
t
t6
t6
t7
t7
Kreisbewegung
Wir erkennen:
-ymax
Schatten
Zeit-Ort-Funktion
y( t ) = y max ⋅ sin(ϕ( t ))
ϕ (t) ist der Phasenwinkel (oder auch die Phase) einer Schwingung zu einem bestimmten
Zeitpunkt t. Er gibt den Winkel im Bogenmaß an, den der Radiusvektor in der zugehörigen
Kreisbewegung mit der positiven x*-Achse einschließt.
Für ϕ (t) gilt allgemein:
⇒ allgemein gilt:
ϕ( t ) = ω ⋅ t + ϕ0 ,
ϕ0 ist dabei der Phasenwinkel zur Zeit t = 0s
y( t ) = y max ⋅ sin(ω ⋅ t + ϕ0 )
Zeit-Ort-Funktion
Die Zeit-Geschwindigkeits-Funktion und die Zeit-Beschleunigungs-Funktion lassen sich nun mit
Hilfe der Differenzialrechnung schnell bestimmen.
2
r
Kurzer Rückblick zur geradlinigen Bewegung mit konstanter Beschleunigung a in x-Richtung:
∆x d
= x ( t ) = x& ( t )
∆t → 0 ∆t
dt
Momentangeschwindigkeit v(t): v( t ) = lim
mit x ( t ) = 12 at 2 + v 0 t + x 0
Momentanbeschleunigung a(t):
⇒
∆v d
= v( t ) = v& ( t )
∆t → 0 ∆t
dt
a ( t ) = lim
mit v( t ) = at + v0
⇒
v( t ) = at + v0
(= &x&( t ))
a ( t ) = a = kons tan t
oder mit Hilfe der Integration von a = kons tan t zu v(t) und von v(t) zu x(t)
Zeit-Geschwindigkeits-Funktion:
v( t ) = y& ( t ) =
⇒
d
bedeutet, dass die
dt
nachfolgende Funktion nach der Zeit t
abgeleitet werden muss)
d
d
y( t ) = ( y max ⋅ sin(ωt + ϕ0 ))
dt
dt
(Hinweis:
v( t ) = y max ⋅ ω ⋅ cos(ωt + ϕ0 )
mit v max = y max ⋅ ω
, denn cos(ωt + ϕ0 ) wird max imal 1
Zeit-Beschleunigungs-Funktion:
a ( t ) = v& ( t ) =
⇒
d
d
v( t ) = ( y max ⋅ ω ⋅ cos(ωt + ϕ0 ))
dt
dt
a ( t ) = − y max ⋅ ω2 ⋅ sin(ωt + ϕ0 )
mit a max = y max ⋅ ω2
Zusammenfassung der Bewegungsgleichungen:
y( t ) = y max ⋅ sin(ωt + ϕ0 )
v( t ) = y max ⋅ ω ⋅ cos(ωt + ϕ0 )
a ( t ) = − y max ⋅ ω2 ⋅ sin(ωt + ϕ0 )
Definition: Eine lineare Schwingung, für die gilt: y( t ) = y max ⋅ sin(ωt + ϕ0 ) ,
bezeichnet man als harmonische Schwingung.
Eine solche Schwingung stimmt mit der Projektion einer Kreisbewegung überein.
Aufgabe:
Drücken Sie a(t) mit Hilfe von y(t) aus.
Weitere Aufgaben zu den Bewegungsgleichungen
3
8.2.1 Das lineare Kraftgesetz
Wir suchen eine Bedingung, mit deren Hilfe sich die harmonische Schwingung theoretisch
r
nachweisen lässt. Dazu betrachten wir die Ursache der Bewegung – die resultierende Kraft F .
r
r
Nach dem Grundgesetz der Mechanik gilt: F( t ) = m ⋅ a ( t )
Betrachten wir eine lineare Schwingung, reicht es, die zugehörige Koordinate zu betrachten.
⇒
F( t ) = m ⋅ a ( t )
mit a ( t ) = − y max ⋅ ω2 ⋅ sin(ωt + ϕ0 )
⇒
F( t ) = − m ⋅ y max ⋅ ω2 ⋅ sin(ωt + ϕ0 )
mit y max ⋅ sin(ωt + ϕ0 ) = y( t )
⇒
F( t ) = − m ⋅ ω2 ⋅ y( t )
⇒
Da m und ω während der harmonischen Schwingung
konstant sind, fasst man diese zusammen:
m ⋅ ω2 = D = kons tan t . D nennt man Richtgröße der
harmonischen Schwingung.
F( t ) = −D ⋅ y( t ) mit D = konstant
Diesen Zusammenhang bezeichnet man als lineares Kraftgesetz. Es besagt, dass bei einer
harmonischen Schwingung die resultierende Kraft direkt proportional zur Elongation aber immer
entgegengerichtet ist.
Man kann auch sagen, dass die resultierende Kraft bei einer harmonischen Schwingung den Körper
immer zur Ruhelage hin beschleunigt. Aus diesem Grund nennt man hier die resultierende Kraft
auch Rückstellkraft oder rücktreibende Kraft.
F( t ) = − D ⋅ y( t ) mit F( t ) = m ⋅ a ( t )
⇒ m ⋅ a ( t ) = − D ⋅ y( t ) mit a ( t ) = &y&( t )
⇒ m ⋅ &y&( t ) = −D ⋅ y( t )
Hinweis auf Differenzialgleichung möglich:
⇒ &y&( t ) +
D
m
⋅ y( t ) = 0
Die letzte Gleichung ist die so genannte Differenzialgleichung der linearen harmonischen
Schwingung. Ihre Lösung erfordert spezielle Verfahren der Analysis und liefert die
Bewegungsgleichungen.
Aus den Überlegungen des linearen Kraftgesetzes zur Richtgröße kann man eine Formel für die
Periodendauer der harmonischen Schwingung schlussfolgern:
m ⋅ ω2 = D ⇒ ω =
⇒
T = 2π ⋅
D
m
mit ω =
2π
T
⇒
2π
=
T
D
m
m
D
4
Zusammenfassung:
Eine harmonische Schwingung lässt sich auf zwei Arten festlegen:
1. eine lineare Schwingung, die mit der Projektion einer Kreisbewegung übereinstimmt. Für eine
solche Schwingung gilt die Bewegungsgleichung y( t ) = y max ⋅ sin(ωt + ϕ0 ) .
(nur praktisch möglich)
2. eine lineare periodische Bewegung, die durch die resultierende Kraftkoordinate F
hervorgerufen wird, für die ein lineares Kraftgesetz der Form F = −D ⋅ y gilt, wobei D konstant
sein muss.
8.2.2 Beispiele harmonischer Schwingungen
a) Schraubenfeder, Gummiseil
Gegeben:
- die Masse der Feder bzw. des Gummis ist vernachlässigbar klein
- Feder/Gummi wird nur im Elastizitätsbereich betrieben (also in dem Bereich, in
dem das Hooksche Gesetz gilt) und nur auf Zug belastet
- D* sei die Federhärte
) Experiment zeigen
) Video schwingender Körper
) Video schwingender Körper mit resultierender Kraft
Serienbild aus Video schwingender Körper mit resultierender Kraft:
Die Schüler erhalten folgende Kopie :
y
y0
unbelastete
Feder
FR
FR
0
Ruhelage
FR
FR
5
Bei verschiedenen Federstellungen der Schwingung ist die resultierende Kraft eingetragen.
Auftrag: Zeichnen Sie in Partnerarbeit an den Körper jeder Federstellung die Teilkräfte ein, die
r
die Rückstellkraft FR hervorrufen.
r
r
r
Lösung: Rückstellkraft FR , Gewichtskraft FG , Federkraft FF
y
y0
unbelastete
Feder
FF
FF
FF
0
FF
FR
Ruhelage
FR
FG
FR
FG
FG
FF
FR
FG
FG
Nachweis der harmonischen Schwingung unter Benutzung der Koordinaten:
r r
r
Hinweis: Es handelt sich um eine lineare Bewegung in y-Richtung. Für die Koordinaten der Kräfte FR , FG und FF
in y-Richtung müsste man nun schreiben FR y , FG y und FFy . Da diese Kräfte aber nur eine y-Komponente
besitzen, wird auf den Index „y“ verzichtet.
r
r
r
Schwingt die Oberkante des Pendelkörpers durch die Ruhelage, dann gilt: FF + FG = 0
Folglich gilt für die Koordinaten: FF + FG = 0 ⇒ D * ⋅y0 + m ⋅ g = 0 . (beachte: g = −9,81 m
)
s²
Allgemein gilt für die Rückstellkraft:
Folglich gilt für die Koordinaten:
r
r r
FR = FF + FG
FR = FF + FG
FR = D * ⋅( y0 − y) + m ⋅ g
FR = D * ⋅y 0 − D * ⋅y + m ⋅ g
mit Gleichgewichtsbedingung D * ⋅y 0 + m ⋅ g = 0
FR = −D * ⋅y
Da D* konstant ist, gilt D = D * ⇒ FR = − D ⋅ y ⇒ Es gilt ein lineares Kraftgesetz, also liegt eine
harmonische Schwingung vor.
6
Nachweis der harmonischen Schwingung unter Benutzung der Beträge:
r
r
r
Schwingt die Oberkante des Pendelkörpers durch die Ruhelage, dann gilt: FF + FG = 0
r
r
r
r
Folglich gilt für die Beträge: | FF |=| FG | ⇒ D * ⋅ | y0 |= m⋅ | g | . (Gleichgewichtsbedingung)
r
r r
FR = FF + FG
Allgemein gilt für die Rückstellkraft:
Folglich sind für die Beträge zwei Fälle zu unterscheiden:
r
r
1. Die Oberkante des Pendelkörpers befindet sich in oder über der Ruhelage ( | FF |≤| FG | ):
r
r
r
| FR |=| FG | − | FF |
r
r
r
r
| FR |= m⋅ | g | −D * ⋅(| y 0 | − | y |)
r
r
r
r
r
r
| FR |= m⋅ | g | −D * ⋅ | y 0 | + D * ⋅ | y |
mit Gleichgewichtsbedingung D * ⋅ | y 0 |= m⋅ | g |
r
r
| FR |= D * ⋅ | y |
r
r
2. Die Oberkante des Pendelkörpers befindet sich unter der Ruhelage ( | FF |>| FG | ):
r
r
r
| FR |=| FF | − | FG |
r
r
r
r
| FR |= D * ⋅(| y 0 | + | y |) − m⋅ | g |
r
r
r
r
r
r
| FR |= D * ⋅ | y 0 | + D * ⋅ | y | − m⋅ | g |
mit Gleichgewichtsbedingung D * ⋅ | y 0 |= m⋅ | g |
r
r
| FR |= D * ⋅ | y |
r
r
In beiden Fällen sind FR und y immer entgegengesetzt orientiert. Demnach gilt für die
Koordinaten: FR = − D * ⋅y .
Da D* konstant ist, gilt D = D * ⇒ FR = − D ⋅ y ⇒ Es gilt ein lineares Kraftgesetz, also liegt eine
harmonische Schwingung vor.
Für die Periodendauer gilt damit: D = D * ⇒ T = 2π ⋅
m
D*
r
| ∆F |
Experimentelle Überprüfung: statische Bestimmung von D* D* = r = ...
| ∆s |
Trechnerisch = 2π ⋅
m
= ...
D*
Texp erimentell = ...
7
Kombination von Schraubenfedern:
a) Zwei Federn mit den Federhärten D1 und D2 werden vertikal hintereinander gehängt.
Welche Federhärte Dges besitzt dieses System?
D1
D2
D1
Dges
y2
y1
D2
50g
50g
FG
FG
yges= y1+ y2
50g
F
G
r
r
r
Die gleiche Kraft FG dehnt die Feder 1 um y1 , die Feder 2 um y 2 und das Federsystem um
r
r
r
r
r
yges . Dabei gilt: FG1 = FG 2 = Fges = FG = konstant
r
r
r
r
| y ges | = y1 + y 2 | : | FG |
r
r
r
r
| yges |
y1
y2
r
r
= r + r
mit | F |= D⋅ | y |
| FG |
| FG | | FG |
⇒
1
1
1
=
+
D ges D1 D 2
D1 = D 2 ⇒ D ges =
Spezialfall:
b) Zwei Federn mit den Federhärten D1 und D2 werden parallel (ineinander) aufgehängt.
Welche Federhärte Dges besitzt dieses System?
D1
D2
D1
y0
y0
F1
D2
Dges
y0
F2
Fges = F2+ F1
r
r
Um die Feder 1 um y0 zu dehnen ist die Kraft F1 notwendig. Bei der Feder 2 benötigt man
r
dazu die Kraft F2 . Beim parallel geschalteten Federsystem erhält man die gleiche Dehnung
r
r r
mit der Kraft Fges = F1 + F2 .
r
r
r
also:
y1 = y 2 = y 0 = konstant
r
r
r
r
| Fges | = | F1 | + | F2 | | : y 0
r
r
r
r
| Fges | | F1 | | F2 |
|F|
= r + r
mit D = r
r
y0
y0
y0
y
⇒ D ges = D1 + D 2
Spezialfall:
D1 = D 2 ⇒ D ges =
8
b) Wagen zwischen zwei gespannten Federn
Gegeben:
- die Massen der Federn sind vernachlässigbar klein
- die Feder wird nur im Elastizitätsbereich betrieben (also in dem Bereich, in dem
das Hooksche Gesetz gilt) und nur auf Zug belastet
- die Federhärte beider Federn sei D*
) Experiment zeigen
) Video
) Video mit resultierender Kraft
Die Schüler erhalten folgende Kopie :
D1=D*
s0
s0
D2=D*
s
0
s
0
FR
s
0
FR
0
s
Bei verschiedenen Elongationen der Schwingung ist die resultierende Kraft eingetragen.
Auftrag: Zeichnen Sie in Partnerarbeit in die unteren drei Bilder jeweils alle auf den Wagen
r
wirkenden Teilkräfte ein, so dass sich die Rückstellkraft FR ergibt.
9
r
r
r
Lösung: Rückstellkraft FR , Gewichtskraft FG , Kraft durch die Unterlage FU , Federkraft nach
r
r
links Fli und Federkraft nach rechts Fre
D1=D*
s0
s0
D2=D*
s
0
FU
Fre
Fli
FG
s
0
FU
Fli
FR
Fre
FG
s
0
FR
Fli
FU
Fre
FG
0
Nachweis der harmonischen Schwingung unter Benutzung der Koordinaten:
s
r
r
Hinweis: Es handelt sich um eine lineare Bewegung in s-Richtung. Für die Koordinaten der Kräfte FR , Fli und
r
Fre in s-Richtung wird folgende Schreibweise gewählt: FR , Fli und Fre . Die Gewichtskraft und die
r
Gegenkraft der Unterlage heben sich immer auf. Sie haben keinen Einfluss auf FR . Es gilt s ≤ s0 .
r
r r
FR = Fli + Fre
Allgemein gilt für die Rückstellkraft:
Folglich gilt für die Koordinaten:
FR = Fli + Fre
FR = −D * ⋅(s 0 + s) + D * ⋅(s 0 − s)
FR = −D * ⋅s 0 − D * ⋅s + D * ⋅s 0 − D * ⋅s
FR = −2 ⋅ D * ⋅s
Da D* konstant ist, gilt D = 2D * ⇒ FR = − D ⋅ s ⇒ Es gilt ein lineares Kraftgesetz, also liegt eine
harmonische Schwingung vor.
10
Nachweis der harmonischen Schwingung unter Benutzung der Beträge:
r
r r
Allgemein gilt für die Rückstellkraft:
FR = Fli + Fre
Folglich sind für die Beträge zwei Fälle zu unterscheiden:
r
r
1. Für die Zeigerstellung gilt s ≥0 ( | Fli |≥| Fre | ):
r
r
r
| FR |=| Fli | − | Fre |
r
r
r
r
r
| FR |= D * ⋅(| s0 | + | s |) − D * ⋅(| s0 | − | s |)
r
r
r
r
r
| FR |= D * ⋅(| s0 | + | s | − | s0 | + | s |)
r
r
r
| FR |= D * ⋅(| s | + | s |)
r
r
| FR |= 2D * ⋅ | s |
r
r
2. Für die Zeigerstellung gilt s < 0 ( | Fre |>| Fli | ):
r
r
r
| FR |=| Fre | − | Fli |
r
r
r
r
r
| FR |= D * ⋅(| s0 | + | s |) − D * ⋅(| s0 | − | s |)
r
r
r
r
r
| FR |= D * ⋅(| s0 | + | s | − | s0 | + | s |)
r
r
| FR |= 2D * ⋅ | s |
r
r
In beiden Fällen sind FR und s immer entgegengesetzt orientiert. Demnach gilt für die
Koordinaten: FR = −2D * ⋅s .
Da D* konstant ist, gilt D = 2D * ⇒ FR = − D ⋅ s ⇒ Es gilt ein lineares Kraftgesetz, also liegt eine
harmonische Schwingung vor.
Für die Periodendauer gilt damit: D = 2D * ⇒ T = 2π ⋅
m
2D *
r
| ∆F |
Experimentelle Überprüfung: statische Bestimmung von D* D* = r = ...
| ∆s |
Trechnerisch = 2π ⋅
m
= ...
2D *
Texp erimentell = ...
11
c) Fadenpendel
Gegeben:
- die Masse des Fadens ist gegenüber der Masse des angehängten Körpers
vernachlässigbar
- der Körper wird als Massenpunkt betrachtet (mathematisches Pendel)
- die Länge vom Aufhängepunkt bis zum Massenpunkt ist l
) Experiment zeigen
) Video Fadenpendel mit kleinem Auslenkwinkel und resultierender Kraft
Die Schüler erhalten folgende Kopie :
1. Körper befindet sich im Umkehrpunkt
l
2. Körper schwingt durch die Ruhelage
α
S
-smax
S
-smax
smax
0
smax
v
FG
3. Körper wird für s < smax vereinfachend
als ruhend angenommen (statischer Fall)
0
4. Der Bewegungszustand des Körpers wird
für s < smax berücksichtigt (dynamischer Fall)
α
α
S
-smax
smax
S
-smax
0
smax
0
v
r
Der Körper wird bei verschiedenen Elongationen betrachtet. FG sei die Gewichtskraft des
r
Pendelkörpers, v die Momentangeschwindigkeit.
Auftrag: Zeichnen Sie in Partnerarbeit in die ersten drei Bilder jeweils alle auf den Pendelkörper
r
wirkenden Teilkräfte ein, so dass sich die Rückstellkraft FR ergibt.
Zum vierten Bild:
) Video mit großem Auslenkwinkel und resultierender Kraft
Gemeinsam wird der Kräfteplan für das vierte Bild erstellt.
12
r
r
r
r
Lösung: Gewichtskraft FG , Fadenkraft FF , Rückstellkraft FR , Zentripetalkraft FZ , resultierende
r
Kraft Fres
1. Körper befindet sich im Umkehrpunkt
l
α
FF
FF
S
-smax
FG
2. Körper schwingt durch die Ruhelage
FR
FZ
-smax
smax
0
S
smax
0
v
FG
3. Körper wird für s < smax vereinfachend
als ruhend angenommen (statischer Fall)
4. Der Bewegungszustand des Körpers wird
für s < smax berücksichtigt (dynamischer Fall)
α
α
FF
smax
-smax
0
FR
FF
S
Fres FZ
-smax
0
FG
S
smax
v
FG
Feststellung: Die resultierende Kraft ist unter Beachtung der Zentripetalkraft nicht tangential zur sAchse. Dieser Effekt ist um so größer, je größer der zu smax gehörende Winkel αmax
gewählt wird. (Vergleich der Videos mit resultierender Kraft für α max = 10° und
α max = 60° ).
⇒ Für kleine Auslenkwinkel kann die s-Komponente der resultierenden Kraft, also die
Rückstellkraft, in guter Näherung aus dem Kräfteplan des statischen Falls ermittelt werden.
Hinweis: Betrachtet man den Fall: αmax = 8,00° = 0,140rad und l = 1,00m
⇒ in der Ruhelage gilt: Der Betrag der Zentripetalkraft ist kleiner als 2% des Betrages der Gewichtskraft.
⇒ für α = 4,00° = 0,070rad gilt:
Der Betrag der Zentripetalkraft ist kleiner als 1,5% des Betrages der Gewichtskraft.
Die Auswirkungen auf die s-Komponente der resultierenden Kraft sind im Verhältnis
zur tangential wirkenden Rückstellkraft noch geringer.
13
Nachweis der harmonischen Schwingung unter Benutzung der Koordinaten:
Aus dem Kräfteplan (1. oder 3.) ergibt sich:
r
r
r
| FR |=| FG | ⋅ sin α = m⋅ | g | ⋅ | sin α |
r
r
Die Rückstellkraft FR und die Elongation s sind entgegengesetzt. Gesteht man dem Winkel α die
r
selbe Orientierung wie s zu, so gilt:
r
FR = − m⋅ | g | ⋅ sin α
mit α =
s
(α im Bogenmaß)
l
r
s
FR = − m⋅ | g | ⋅ sin( )
l
Man erkennt, dass hierbei zunächst noch kein lineares Kraftgesetz gilt. Genau genommen handelt es
sich beim Fadenpendel also nicht um eine harmonische Schwingung.
Für kleine Auslenkwinkel α kann man jedoch auf die Kleinwinkelnäherung zurückgreifen:
s
s
π = 10° ist der Fehler hierbei kleiner als
sin α ≈ α ⇒ sin( ) ≈
Für α = 18
ˆ
l
l
0,51%.
r
r s
m⋅ | g |
⇒ FR = −m⋅ | g | ⋅ = −
⋅s
l
l
r
r
m⋅ | g |
⇒ FR = −D ⋅ s
Da m, | g | und l konstant sind, gilt D =
l
⇒ Es gilt ein lineares Kraftgesetz, also liegt für
kleine Winkel eine (näherungsweise)
harmonische Schwingung vor.
Nachweis der harmonischen Schwingung unter Benutzung der Beträge:
Aus dem Kräfteplanr(1. oder
r 3.) ergibt sich:r
| FR |=| FG | ⋅ | sin α |= m⋅ | g | ⋅ | sin α |
r
r
s
| FR |= m⋅ | g | ⋅ | sin α |
mit α = (α im Bogenmaß)
l
r
r
s
| FR |= m⋅ | g | ⋅ | sin( ) |
l
Man erkennt, dass hierbei zunächst noch kein lineares Kraftgesetz gilt. Genau genommen handelt
es sich beim Fadenpendel also nicht um eine harmonische Schwingung.
Für kleine Auslenkwinkel α kann man jedoch auf die Kleinwinkelnäherung zurückgreifen:
s
s
π = 10° ist der Fehler hierbei kleiner
sin α ≈ α ⇒ sin( ) ≈
Für α = 18
ˆ
l
l
als 0,51%.
r
r
r
r | s | m⋅ | g | r
⇒ | FR |= m⋅ | g | ⋅
|=
⋅| s |
l
l
r
r
r
m⋅ | g |
FR und s sind immer entgegengesetzt orientiert, also gilt für die Koordinaten: FR = −
⋅s .
l
r
r
m⋅ | g |
Da m, | g | und l konstant sind, gilt D =
⇒ FR = −D ⋅ s
l
⇒ Es gilt ein lineares Kraftgesetz, folglich liegt
für kleine Winkel eine (näherungsweise)
harmonische Schwingung vor.
14
r
m⋅ | g |
Für die Periodendauer gilt damit: D =
l
⇒ T = 2π ⋅
m
l
= 2π ⋅ r
D
|g|
l = ...
Experimentelle Überprüfung:
Trechnerisch = 2π ⋅
l
r = ...
|g|
Texp erimentell = ...
d) schwingende Flüssigkeitssäule im U-Rohr
Gegeben:
- U-Rohr mit konstanter Querschnittsfläche A = π ⋅ r 2
- homogene Flüssigkeit der Dichte ρ
- Flüssigkeitssäule der Länge l
- „-ymax“ muss über dem gekrümmten Bereich des U-Rohres liegen
) Experiment zeigen
Nachweis der harmonischen Schwingung unter Benutzung der Koordinaten:
Die rechte Oberkante der schwingenden Flüssigkeitssäule zeigt die jeweilige Elongation y an.
Skizze:
y
r
ymax
mü
0
-ymax
m
r
FR ( t ) = − | g | ⋅m ü ( t )
r
⇒ FR = − | g | ⋅ρ ⋅ π ⋅ r 2 ⋅ 2 y
m – gesamte Masse der Flüssigkeit
mü – Masse der überstehenden Flüssigkeit
Die für die Schwingung verantwortliche
Rückstellkraft ist hierbei die Gewichtskraft der
r
überstehenden Flüssigkeit FGü .
Befindet sich diese im rechten Schenkel, so wirkt
r
FGü entgegen der y-Achse, befindet sich diese im
r
linken Schenkel, so wirkt FGü in Richtung der yAchse.
Die Masse mü wird dadurch zu einer
vorzeichenbehafteten Größe, die sich zeitlich
ändert. Die überstehende Flüssigkeit hat das
Volumen Vü und die Höhe 2y. Beide Größen sind
ebenfalls vorzeichenbehaftet und zeitlich
abhängig.
mit m ü ( t ) = ρ ⋅ Vü ( t ) = ρ ⋅ π ⋅ r 2 ⋅ 2 y( t )
r
r
Da | g | , ρ und r konstant sind, gilt D = 2π⋅ | g | ⋅ρ ⋅ r 2 ⇒ FR = −D ⋅ y
⇒ Es gilt ein lineares Kraftgesetz, also liegt
eine harmonische Schwingung vor.
15
Nachweis der harmonischen Schwingung unter Benutzung der Beträge:
Die rechte Oberkante der schwingenden Flüssigkeitssäule zeigt die jeweilige Elongation y an.
Skizze:
r
m – gesamte Masse der Flüssigkeit
mü – Masse der überstehenden Flüssigkeit
y
ymax
mü
0
-ymax
m
Die für die Schwingung verantwortliche
r
Rückstellkraft ist hierbei die Gewichtskraft FGü
der überstehenden Flüssigkeit.
Befindet sich diese im rechten Schenkel, so wirkt
r
FGü entgegen der y-Achse, befindet sich diese im
r
linken Schenkel, so wirkt FGü in Richtung der yAchse.
Die Masse mü wird dadurch zu einer
vorzeichenbehafteten Größe, die sich zeitlich
ändert. Die überstehende Flüssigkeit hat das
Volumen Vü und die Höhe 2y. Beide Größen sind
ebenfalls vorzeichenbehaftet und zeitlich
abhängig.
r
r
r
| FR ( t ) |=| g | ⋅ | m ü ( t ) |
mit | m ü ( t ) |= ρ⋅ | Vü ( t ) |= ρ ⋅ π ⋅ r 2 ⋅ 2 | y( t ) |
r
r
r
⇒ | FR |=| g | ⋅ρ ⋅ π ⋅ r 2 ⋅ 2 | y |
r
r
r
FR und y sind immer entgegengesetzt orientiert. Es gilt für die Koordinaten: FR = − | g | ⋅ρ ⋅ π ⋅ r 2 ⋅ 2 y .
r
r
Da | g | , ρ und r konstant sind, gilt D = 2π⋅ | g | ⋅ρ ⋅ r 2 ⇒ FR = −D ⋅ y
⇒ Es gilt ein lineares Kraftgesetz, also liegt
eine harmonische Schwingung vor.
r
Bestimmung der Periodendauer: D = 2π⋅ | g | ⋅ρ ⋅ r 2
und T = 2π ⋅
m
D
m ist hierbei die gesamte schwingende Masse: m = ρ ⋅ V = ρ ⋅ π ⋅ r 2 ⋅ l
m
ρ ⋅ π ⋅ r2 ⋅ l
l
⇒ T = 2π ⋅
= 2π ⋅
= 2π ⋅
r
r
2
D
2|g|
2π⋅ | g | ⋅ρ ⋅ r
Experimentelle Überprüfung:
l = ...
Trechnerisch = 2π ⋅
l
r = ...
2|g|
Texp erimentell = ...
16