Solve( 0.00618 x*sin2 (1125s/0,5s 0,13m/0,1m),x) − = π
Werbung
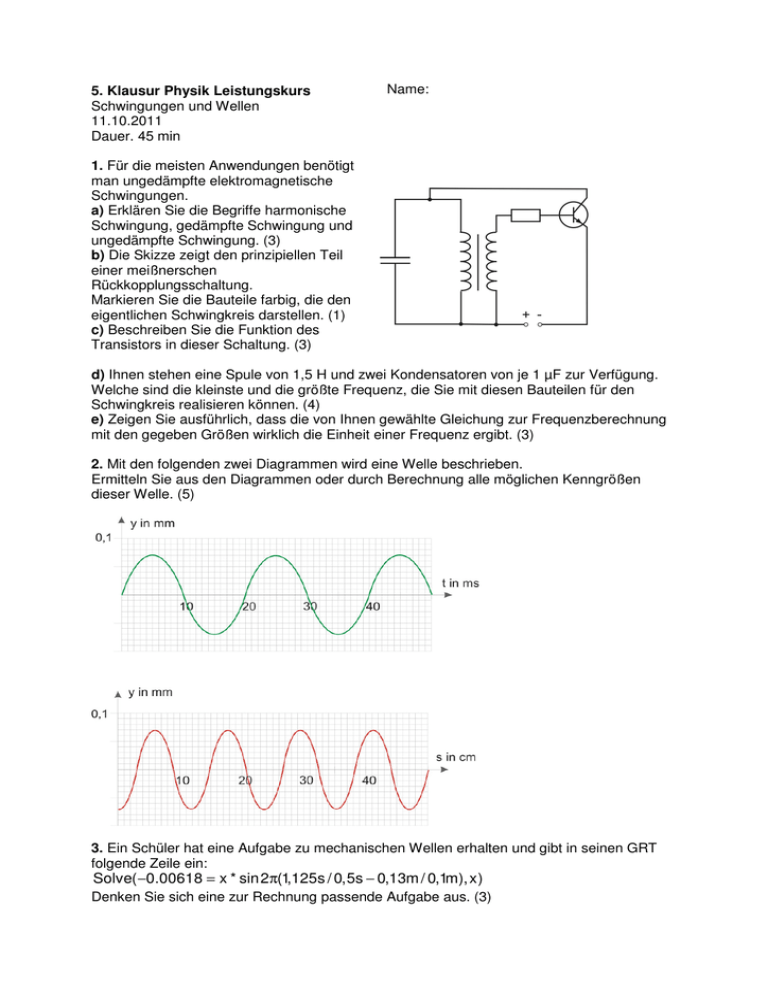
5. Klausur Physik Leistungskurs Schwingungen und Wellen 11.10.2011 Dauer. 45 min Name: 1. Für die meisten Anwendungen benötigt man ungedämpfte elektromagnetische Schwingungen. a) Erklären Sie die Begriffe harmonische Schwingung, gedämpfte Schwingung und ungedämpfte Schwingung. (3) b) Die Skizze zeigt den prinzipiellen Teil einer meißnerschen Rückkopplungsschaltung. Markieren Sie die Bauteile farbig, die den eigentlichen Schwingkreis darstellen. (1) c) Beschreiben Sie die Funktion des Transistors in dieser Schaltung. (3) d) Ihnen stehen eine Spule von 1,5 H und zwei Kondensatoren von je 1 µF zur Verfügung. Welche sind die kleinste und die größte Frequenz, die Sie mit diesen Bauteilen für den Schwingkreis realisieren können. (4) e) Zeigen Sie ausführlich, dass die von Ihnen gewählte Gleichung zur Frequenzberechnung mit den gegeben Größen wirklich die Einheit einer Frequenz ergibt. (3) 2. Mit den folgenden zwei Diagrammen wird eine Welle beschrieben. Ermitteln Sie aus den Diagrammen oder durch Berechnung alle möglichen Kenngrößen dieser Welle. (5) 3. Ein Schüler hat eine Aufgabe zu mechanischen Wellen erhalten und gibt in seinen GRT folgende Zeile ein: Solve( −0.00618 = x * sin2π(1,125s / 0,5s − 0,13m / 0,1m), x) Denken Sie sich eine zur Rechnung passende Aufgabe aus. (3) Lösungen 1. a) harmonische Schwingung: Zur Ruhelage des Schwingers wirkt eine Kraft, die proportional zum Abstand zur Ruhelage ist. gedämpfte Schwingung: Jede freie Schwingung ist gedämpft. Durch Abgabe von Energie wird die Amplitude ständig kleiner. ungedämpfte Schwingung: Durch periodische Energiezufuhr werden die Energieverluste ausgeglichen und die Amplitude bleibt konstant. b) c) Der Transistor wirkt als Schalter. Wenn im Schwingkreis eine Schwingung stattfindet, wird in der rechten Spule periodisch eine Spannung induziert. durch diese Spannung wird der Transistor über die Basis periodisch geöffnet und geschlossen und liefert in den Schwingkreis Energie. Damit werden die Verluste im Schwingkreis ausgeglichen und es läuft eine ungedämpfte Schwingung ab. d) Die Gleichung für die Frequenz im Schwingkreis lautet: f= 1 2 ⋅ π⋅ L ⋅ C Die Induktivität L ist gegeben. Die Kondensatoren können in Reihe oder Parallel geschaltet werden. In Reihe ergeben sie 0,5 µF und Parallel 2 µF. Damit lassen sich die Frequenzen berechnen: f= 1 2 ⋅π⋅ 1,5H ⋅ 0,5 ⋅10 −6 F f1 = 184Hz f2 = 92Hz e) [f ] =1 1 1H ⋅1F 1 [f ] =1 1 1 [f ] =1 1 1 [f ] =1 m2 ⋅ kg ⋅ s s2 ⋅ A ⋅ V 1 [f ] =1 [f ] =1 m2 ⋅ kg A ⋅ s ⋅1 s2 ⋅ A 2 V m ⋅N⋅ s A⋅V 1 m ⋅N⋅ s 1 W 1 W ⋅s⋅s W 1 1 [f ] =1 [f ] =1 1s2 1 = 1Hz s 2. Aus dem ersten Diagramm kann man ablesen: y max = 0,07mm T = 20ms Das zweite Diagramm liefert λ = 12cm Daraus kann die Frequenz und die Ausbreitungsgeschwindigkeit berechnet werden: f= 1 T 1 20ms f = 50Hz f= 3. Die Aufgabe muss folgende Tatsachen enthalten: a) Gesucht ist die Amplitude. b) Die Welle hat die Schwingungsdauer 0,5 s (Frequenz 2 Hz) und die Wellenlänge 0,1 m c) 1,125 s nach dem Start der Welle hat ein Punkt 0,13 m vom Startpunkt entfernt eine Auslenkung von 0,00618 m nach unten.









![366 offener Schwingkreis [tra]](http://s1.studylibde.com/store/data/007200915_1-9ff66afdf8f7b9be4ff1abb305d78750-300x300.png)
