Hertzscher Dipol und elektromagnetische Welle - Hans

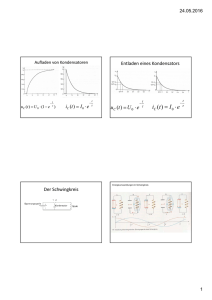
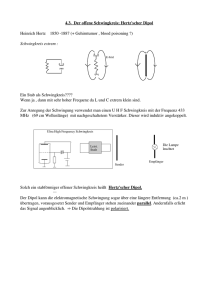
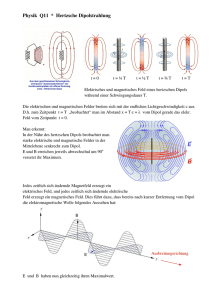
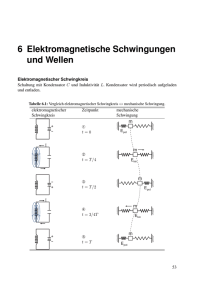
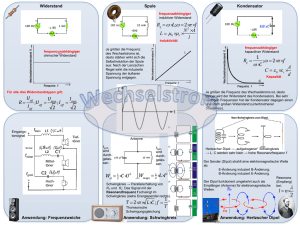
Achtung: Die Punkteverteilung ist nicht optimal.
K12
–
LK Physik
-
4. Klausur
am 14.7.2005
1) Hertzscher Dipol und elektromagnetische Welle
Ein stabförmiger elektrischer Oszillator (Dipol) kann zu Oberschwingungen angeregt
werden.
2
a) Zeichnen sie die Stromstärkeverteilung für die 1. Oberschwingung.
1
b) Was bedeutet es akustisch, wenn die Luftsäule in einer Trompete in der 1. Oberschwingung
schwingt ?
4
c) Ein Dipol wird mit einem Sender der Frequenz 434 MHz in der 2. Oberschwingung
angeregt. Welche Länge hat dieser Dipol ?
4
d) Beschreiben Sie ein Experiment, welches Ihrer Meinung nach am besten geeignet ist, zu
beweisen, dass ein Dipol eine elektromagnetische Welle aussendet. Erläutern Sie
insbesondere die Beweiskraft des von Ihnen angeführten Experiments.
2) Die freie ungedämpfte elektromagnetische Schwingung
4
a) Stellen Sie zunächst die Differentialgleichung für die ungedämpfte Schwingung eines
elektromagnetischen Schwingkreises auf und stellen Sie dann die Differentialgleichung mit
Hilfe der Stromstärke dar.


(d.h. Dgl mit I(t) , I (t ) , I (t ) , ...)
8
b) Wählen Sie zur Lösung dieser Differentialgleichung einen sinnvollen Lösungsansatz für I(t)
und bestimmen Sie damit die Schwingungsformel von Thomson.
3) Ein freier, ungedämpfter elektromagnetischer Schwingkreis
besteht aus einem Kondensator der Kapazität C = 1,0 F
und einer Spule der Induktivität L = 0,040 H.
R sei vernachlässigbar klein.
Der Kondensator wird zu Beginn der Schwingung (t = 0,0 s) mit einer Spannung von 200 V
aufgeladen. Der Schwingkreis wird gestartet. Die Schwingungsdauer sei T.
3
a) Berechnen Sie die Ladung am Kondensator zum Zeitpunkt t = T/6.
5
b) Berechnen Sie einen Zeitpunkt t, zu dem der augenblickliche Spulenstrom genau 50 %
seines maximalen Wertes beträgt.
 weiter 2. Blatt !
2
4) Der radioaktive Zerfall – die zeitliche Abnahme des Ionisationsstroms
Zerfallsvorgänge in der Kernphysik lassen sich mathematisch sehr ähnlich wie
Ausschaltvorgänge bei Spulen oder Entladevorgänge bei Kondensatoren beschreiben.
Mit einer „Ionisationskammer“ wird der zeitliche Verlauf des radioaktiven Zerfalls des
Gases Rn220 untersucht. Die Versuchsdurchführung ergibt folgende Messwerte für die
Stärke des von Rn200 verursachten Ionisationsstroms I in Abhängigkeit von der Zeit t:
t [s]
I [10-11 A]
6
2
3
0
40
10
35,2
20
31,2
30
27,2
40
24
50
21,2
60
18,8
70
16,4
80
14,4
90
12,8
100
11,2
a) Zeigen Sie unter Verwendung dieser Messwerte mittels eines geeigneten graphischen
Verfahrens, dass die Stromstärke exponentiell gemäß der Beziehung
I(t) = I o  e   t abnimmt.
b) Bestimmen Sie mit Hilfe Ihres Graphen die „Zerfallskonstante“  .
c) Wie lange dauert es, bis der Ionisationsstrom auf 10 % des anfänglichen Wertes gesunken
ist ?
5) Der Knoff-hoff-Professor und das BLKA
Nach dem Prinzip der „Induktions-Weidezaun-Schaltung für Kühe“ möchte der Knoff-hoffProfessor als Faschingsscherz eine kleine „Elektrisierschaltung“ bauen. Es stehen ihm zur
Verfügung: Eine 12V-Batterie, eine Spule, deren Induktivität 100 H und deren Widerstand
200 Ohm beträgt , ein elektronischer Schalter (gewöhnliches Schaltersymbol) ,
verschiedene Kabel und ein Schuhkarton. Aus dem Karton führt er zwei „ElektrisierElektroden“ heraus.
3
a) Entwerfen Sie den Schaltplan.
4
b) Skizzieren Sie für den Ein- und den Ausschaltvorgang I(t) und Uind(t)
5
c) Berechnen Sie den Wert der Induktionsspannung unmittelbar nach dem Ausschalten, wenn
der „menschliche Widerstand“ zwischen den beiden Elektrisierkabeln (Berührung
Berührung mit dem linken Arm und dem linken Fuß) 1,4 kOhm beträgt.
6
d) Nun ist die entscheidende Frage, ob diese Schaltung wirklich ungefährlich ist.
Grundlage kriminaltechnischer Untersuchungen des BLKA bei Stromunfällen sind die
„Zeit-Strom-Gefährdungsbereiche“ von Körperreferenzströmen „linke Hand zu linkem
Fuß“ (=ungünstigster Fall). Das in der Anlage beiliegende Diagramm drückt aus, welcher
der vier Gefährdungsbereiche vorliegt, wenn während der Zeit t = ... ms im Körper ein
Strom von I = ... mA fließt. (z.B.: I = 10 mA und t = 10000 ms  Gefährdungsbereich 2)
Weisen Sie (z.B. durch eine geeignete Rechnung) nach, welcher Gefährdungsbereich beim
Ausschaltvorgang vorlag, wenn die Berührung der beiden Elektrisierelektroden tatsächlich
mit der linken Hand und dem linken Fuß erfolgte.
3
Anlage: