6 Elektromagnetische Schwingungen und Wellen

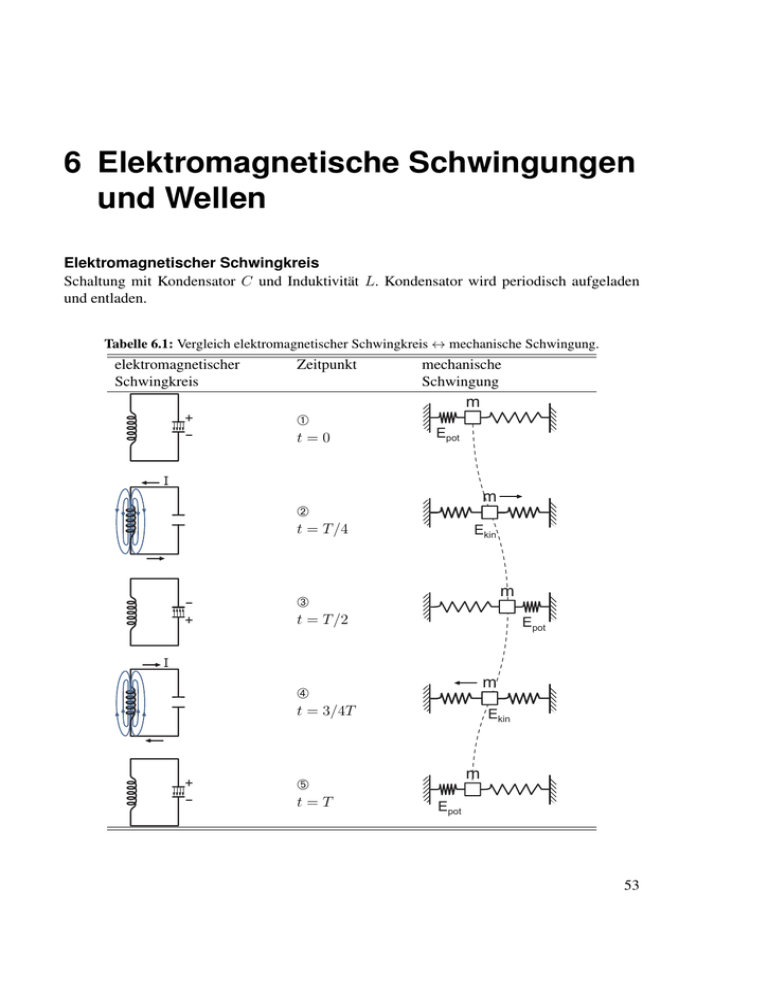
6 Elektromagnetische Schwingungen
und Wellen
Elektromagnetischer Schwingkreis
Schaltung mit Kondensator C und Induktivität L. Kondensator wird periodisch aufgeladen
und entladen.
Tabelle 6.1: Vergleich elektromagnetischer Schwingkreis ↔ mechanische Schwingung.
elektromagnetischer
Schwingkreis
Zeitpunkt
mechanische
Schwingung
m
+
-
À
t=0
Epot
I
m
Á
t = T /4
+
Ekin
m
Â
t = T /2
Epot
I
m
Ã
t = 3/4T
+
-
Ä
t=T
Ekin
m
Epot
53
6 Elektromagnetische Schwingungen und Wellen
Energie im Schwingkreis
a) ungedämpft (R=0):
magnetische Energie in Spule: Wmagn = 21 LI 2
elektrische Energie in Kondensator: Wel = 12 CU 2 =
1 Q2
2 C
Energieerhaltung:
1 2 1 Q2
LI +
= konst.
2
2C
(6.1)
1 2 1 2
mv + Dx = konst.
2
2
(6.2)
d
(Wmagn + Wel ) = IR2
dt
(6.3)
Analogie zur Mechanik (Feder):
b) gedämpft (R6=0):
Zeitliche Abnahme der Energie:
−
Verlustleistung; Energie wird als Wärme entzogen (Joulsche Wärme)
6.1 Freie elektromagnetische Schwingung
L
U
C
R
Abbildung 6.1: LCR-Schwingkreis
dI
dt
Q
UC =
C
UR = RI
UL = L
54
(6.4)
(6.5)
(6.6)
6.1 Freie elektromagnetische Schwingung
Kirchhoffsche Maschenregel:
→ U = UL + UC + UR = 0
dI Q
⇔ L + + RI = 0
dt C
differenzieren
d2 I
1
dI
⇒L 2 +R + I =0
dt
dt C
(6.7)
(6.8)
(6.9)
(6.10)
Analogie zur Mechanik:
m
d2 x
dx
+ b + Dx = 0
2
dt
dt
(6.11)
Lösungsansatz:
I = I0 exp (λt)
dI
= λI0 exp (λt)
dt
d2 I
= λ2 I0 exp (λt)
2
dt
(6.12)
(6.13)
(6.14)
einsetzen:
R
1
λ+
=0
L
LC r
p
R
R2
1
⇒ λ1,2 = −
±
−
=
−α
±
β2
2L
4L2 LC
λ2 +
(6.15)
(6.16)
Verschiedene Schwingfälle je nach Verhältnis von α und β.
a) starke Dämpfung (Kriechfall):
β2 > 0
1
R2
>
⇒
2
4L
LC
(6.17)
(6.18)
55
6 Elektromagnetische Schwingungen und Wellen
b) aperiodischer Grenzfall:
β2 = 0
R2
1
⇒
=
2
4L
LC
(6.19)
(6.20)
c) gedämpfte Schwingung:
β2 < 0
R2
1
⇒
<
2
4L
LC
⇒ I(t) = I0 exp (−λt) cos (ωt + ϕ)
(6.21)
(6.22)
(6.23)
R
mit der Dämpfungskonstante: α =
2L
r
1
R2
und der Frequenz: ω =
− 2
LC 4L
q
ω02 − α2
⇒ω=
mit ω0 =
(6.24)
1
Frequenz der ungedämpften Schwingung α = 0.
LC
I(t)
I0
~e -αt
0
t
-I0
Abbildung 6.2: Amplituden-Zeitdiagramm einer gedämpften Schwingung.
Einfluss der Dämpfung:
→ Abnahme der Amplitude
→ Verschiebung der Resonanzfrequenz
56
(6.25)
6.2 Erzwungene elektromagnetische Schwingung
6.2 Erzwungene elektromagnetische Schwingung
Schwingkreis mit äußerer periodischer Anregung.
L
U0cos ωt
C
R
Abbildung 6.3: LCR-Schwingkreis mit Anregung.
Q
dI
+ RI + = U0 cos (ωt)
dt
C
differenzieren:
d2 I
dI
1
dU
L 2 +R + I =
dt
dt C
dt
L
(6.26)
(6.27)
(6.28)
(6.29)
Der Strom I im Kreis hat eine zeitlich konstante Amplitude I0 =
I = I0 cos (ωt − ϕ)
s
|Z| =
R2
U0
|Z|
mit:
(6.30)
1
+ ωL −
ωC
2
(6.31)
Resonanz für:
ω = ωR = √
⇒ Z(ωR ) = R
1
LC
(6.32)
(6.33)
→ rein reeller Widerstand, ϕ = 0, U und I in Phase.
→ |Z| minimal, I0 maximal.
Anregungstypen:
ω ωR : quasistatische Anregung
ω ≈ ωR : resonante Anregung
ω ωR : hochfrequente Anregung
57
6 Elektromagnetische Schwingungen und Wellen
(a) I0
|Z|
0
0
(b)
_
p
2
wR
w
j
Induktivität
dominiert
0
w
p
-_
2
Kapazität
dominiert
wR
Abbildung 6.4: Frequenzabhängigkeit von (a) Strom I0 und Impedanz Z , sowie (b) der Phase ϕ im
LCR-Reihenschwingkreis.
58
6.3 Offene Schwingkreise, Hertzscher Dipol
6.3 Offene Schwingkreise, Hertzscher Dipol
Im geschlossenen Schwingkreis sind L und C separiert → Übergang zum offenen Schwingkreis.
(a)
C
(b)
L
C
L
(c)
(d)
C+L
C+L
Abbildung 6.5: Entwicklung vom LC-Schwingkreis (a) zum Dipol (d). Aus der Spule wird eine Leiterschlaufe (b) bzw. ein Stab. Der Kondensator wird „aufgebogen“. Die Kapazität wirkt
zwischen den Enden des Stabes (c).
→ keine räumliche Trennung von elektrischem und magnetischem Feld.
E(t)
B(t)
Abbildung 6.6: Elektrisches und magnetisches Feld eines Hertzschen Dipols.
Bei zeitlicher Änderung der Strom- und Ladungsdichte:
→ Änderung der Felder
→ Ausbreitung mit Lichtgeschwindigkeit im Raum
→ Energieverlust durch Abstrahlung elektromagnetischer Wellen
Anregung eines offenen Schwingkreises durch induktive oder kapazitive Kopplung an einen
geschlossenen Kreis. Erhöhung der Resonanzfrequenz durch Verkleinerung von L und C:
1
ωR = √
LC
(6.34)
59
6 Elektromagnetische Schwingungen und Wellen
Strom- und Spannungsverteilung
z
ℓ
I(z,t0)
U(z,t0)
Abbildung 6.7
I(z, t) = I0 (z) sin (ωt)
(6.35)
entspricht einer stehenden Welle mit einer Wellenlänge von λ = 2`.
Niedrigste Resonanzfrequenz:
ω0 =
2π
π
c
c = cPh mit cPh = √
λ
l
µ
(6.36)
cPh : Phasengeschwindigkeit der elektromagnetischen Welle.
Wechselstrom im Stab induziert:
Negativ geladene Elektronen schwingen gegenüber positiv geladenen Atomrümpfen.
→ schwingender, elektrischer Dipol
→ Hertzscher Dipol
-q
+q
Abbildung 6.8: Ladungsbewegung beim Hertzschen Dipol.
d~ = d0 sin (ωt)
p~(t) = q d0 sin (ωt)
⇒ p~(t) = q d~
60
(6.37)
(6.38)
(6.39)
6.4 Elektromagnetische Wellen
Abstrahlcharakteristik:
J
Abbildung 6.9: Abstrahlcharakteristik eines Dipols.
S∝
ω 4 sin2 ϑ
r2
(6.40)
S: Poynting-Vektor gibt die strömende elektromagnetische Feldenergie nach Betrag und Richtung an.
6.4 Elektromagnetische Wellen
Abstrahlung eines Hertzschen Dipols → fortschreitende elektromagnetische Welle mit der
Geschwindigkeit:
Ausbreitungsvektor ~k :
1
0 µ0
2π
ω
|~k| =
=
λ
c
c= √
(6.41)
(6.42)
Wellengleichung
∂ 2E ∂ 2E ∂ 2E
∂ 2E
+
+
=
µ
0
0
∂x2
∂y 2
∂z 2
∂t2
(6.43)
eines zeitlich veränderlichen elektrischen Feldes E(~r, t) im Vakuum
→ periodische, ebene Welle in der Fernzone des Dipols (r λ)
~ =E
~ 0,y sin (kz − ωt)
E
~ =B
~ 0,x sin (kz − ωt)
B
~k ⊥ B
~
~
mit ~k ⊥ E
(6.44)
(6.45)
~ ⊥B
~
E
(6.46)
61