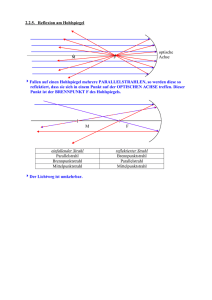
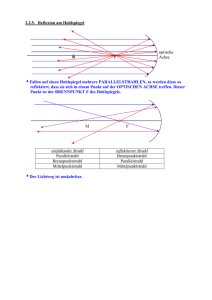
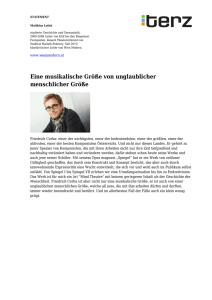
Optische Abbildung durch Reflexion Ebener Spiegel Warum

Optische Abbildung durch Reflexion
Ebener Spiegel
Warum erscheint dem Betrachter dieses Bild so fremd?
Bildkonstruktion am ebenen Spiegel
P1'
P2'
Spiegel
1
Optische Abbildung durch Reflexion
Konkavspiegel-Hohlspiegel
Ableitung der Beziehung zwischen Krümmungsradius und Brennweite
S
Betrachtet werden paraxiale Strahlen, d.h. α ⟨⟨1 .
cos α =
OF =
OF =
OF ≈
R
R
2 ⋅ OF
⋅
1
2 cos α
=
R
2
⋅
1
1 − sin²α
R ⎛⎜
α² ⎞⎟
⋅ ⎜1 +
mit α ⟨⟨1
2 ⎝
2 ⎟⎠
R
2
O- Krümmungsmittelpunkt
F- Brennpunkt
S – Scheitelpunkt
OS- Hauptachse, optische Achse
FS = f Brennweite
Spiegel
2
Ableitung der Abbildungsgleichung für den Hohlspiegel
Voraussetzung: SS’<<OG, OB
1. Betrachtet wird Dreieck GOP:
α + β + ε = 180°
α + β =θ
(1)
ε- Winkel GOP; θ dazugehöriger Außenwinkel
2. Betrachtet wird Dreieck OBP:
θ + α = δ (2)
mit (1) folgt:
2α + β = δ
2α = δ − β
(2’)
(1) multipliziert mit dem Faktor 2 ergibt:
2α + 2 β = 2θ
einsetzen von (2’) δ − β + 2 β = 2θ
δ + β = 2θ
Für kleine Winkel gilt:
Abbildungsgleichung:
Spiegel
β =
1
f
=
1
a
PS
PS
PS r
;δ =
;θ =
; =f
a
a'
r 2
+
1
a'
3
Konkavspiegel - Hohlspiegel
Abbildungsgleichung in Scheitelpunktskoordinaten
Abbildungsmaßstab
β =
y'
a'
=−
Y
a
1
f
=
1
a
+
1
a'
Abbildungsgleichung in Brennpunktskoordinaten f² = xx'
Abbildungsmaßstab
β =
y'
y'
x'
f
=−
=−
; β =
Y
f
Y
x
Bildkonstruktion
1. Parallelstrahl wird zum Brennpunkstrahl
2. Mittelpunktstrahl durch O wird in sich selbst reflektiert
3. Brennpunktstrahl wird zum Parallelstrahl
Spiegel
4
Konvexspiegel – Wölbspiegel
Abbildungsgleichung in Scheitelpunktskoordinaten
Abbildungsmaßstab
β =
y'
a'
=−
Y
a
1
f
=
1
a
+
1
a'
Abbildungsgleichung in Brennpunktskoordinaten f² = xx'
Abbildungsmaßstab
β =
y'
y'
x'
f
=−
=−
; β =
Y
f
Y
x
Bildkonstruktion
1. Parallelstrahl wird zum Brennpunkstrahl
2. Mittelpunktstrahl durch O wird in sich selbst reflektiert
3. Brennpunktstrahl wird zum Parallelstrahl
Spiegel
5