11. Übungsblatt zur Vorlesung „Physik für Pharmazeuten“ 41

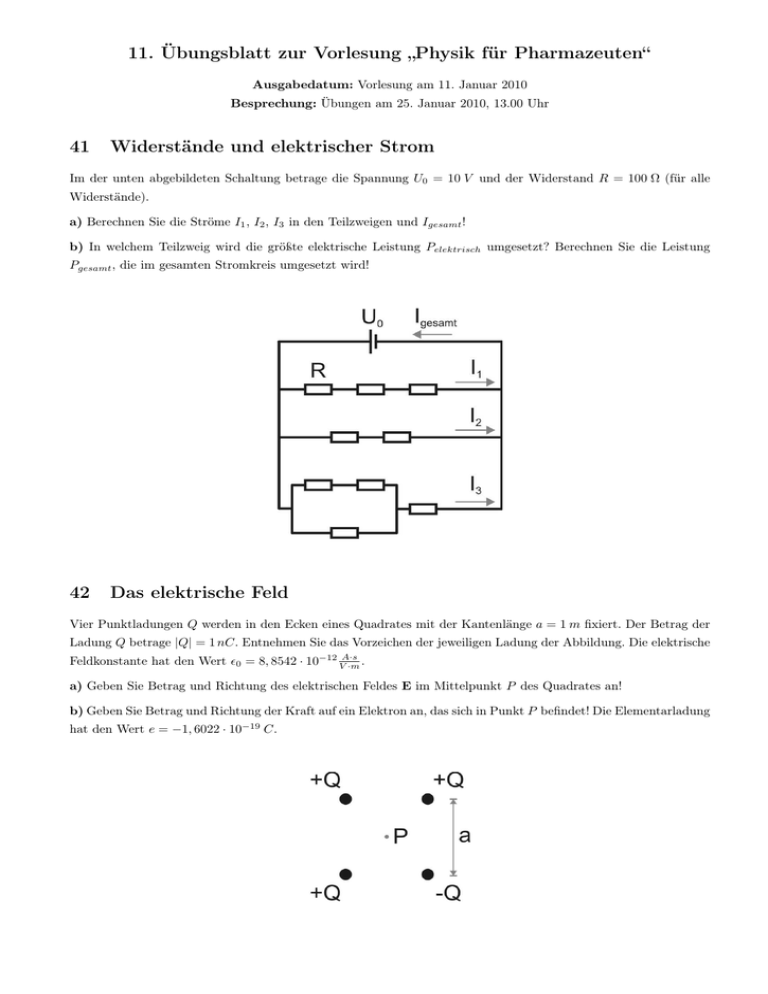
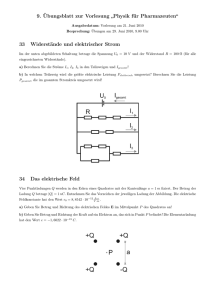
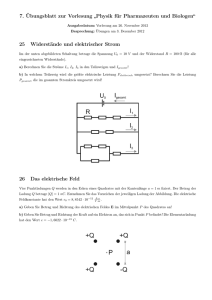
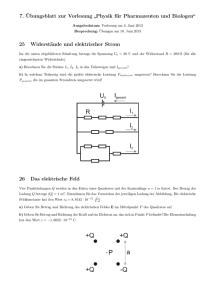
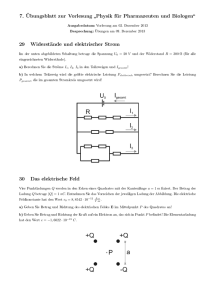
11. Übungsblatt zur Vorlesung „Physik für Pharmazeuten“
Ausgabedatum: Vorlesung am 11. Januar 2010
Besprechung: Übungen am 25. Januar 2010, 13.00 Uhr
41
Widerstände und elektrischer Strom
Im der unten abgebildeten Schaltung betrage die Spannung U0 = 10 V und der Widerstand R = 100 Ω (für alle
Widerstände).
a) Berechnen Sie die Ströme I1 , I2 , I3 in den Teilzweigen und Igesamt !
b) In welchem Teilzweig wird die größte elektrische Leistung Pelektrisch umgesetzt? Berechnen Sie die Leistung
Pgesamt , die im gesamten Stromkreis umgesetzt wird!
42
Das elektrische Feld
Vier Punktladungen Q werden in den Ecken eines Quadrates mit der Kantenlänge a = 1 m fixiert. Der Betrag der
Ladung Q betrage |Q| = 1 nC. Entnehmen Sie das Vorzeichen der jeweiligen Ladung der Abbildung. Die elektrische
Feldkonstante hat den Wert 0 = 8, 8542 · 10−12 VA·s
·m .
a) Geben Sie Betrag und Richtung des elektrischen Feldes E im Mittelpunkt P des Quadrates an!
b) Geben Sie Betrag und Richtung der Kraft auf ein Elektron an, das sich in Punkt P befindet! Die Elementarladung
hat den Wert e = −1, 6022 · 10−19 C.
43
Der Plattenkondensator
In einen Plattenkondensator werde ein Elektron mit der Geschwindigkeit v0 = 593 · 103
m
s
parallel zu den Kon-
densatorplatten eingeschossen. Das Elektron tritt genau in der Mitte zwischen den beiden Kondensatorplatten in
den Kondensator ein. Eine Kondensatorplatte habe eine Fläche von A = 4 · 10−2 m2 , der Plattenabstand betrage
d = 0, 1 m und zwischen den Platten liege eine Spannung von U0 = 1 V an. Die elektrische Feldkonstante hat den
F
−19
= 8, 8542 · 10−12 VA·s
C und die Masse
Wert 0 = 8, 854 · 10−12 m
·m , die Elementarladung beträgt e = −1, 6022 · 10
eine Elektrons beträgt me = 9, 1094 · 10−31 kg.
a) Berechnen Sie die Kapazität C des Kondensators!
b) Berechnen Sie die Ladung Q auf den Kondensatorplatten!
c) Berechnen Sie Betrag und Richtung des elektrischen Feldes E zwischen den Kondensatorplatten!
d) Berechnen Sie den Energieinhalt WC des elektrischen Feldes!
e) Berechnen Sie die Strecke ∆x, die das Elektron in horizontaler Richtung zwischen den Kondensatorplatten zurücklegt, bevor es auf die Kondensatorplatte trifft! Hierfür soll angenommen werden, dass das elektrische Feld im
Inneren des Kondensators homogen ist und außerhalb der Kondensatorplatten E = 0 ist.
44
Elektrostatische Kraft in Atomkernen* [Zusatzaufgabe]
Der Kern eines Eisenatoms hat einen Radius von 4, 0 · 10−15 m und enthält 26 Protonen (Protonenladung +e =
1, 60 · 10−19 C).
a) Wie groß ist die abstoßende elektrostatische Kraft zwischen zwei Protonen des Kerns, die einen Abstand von
4, 0 · 10−15 m haben? [FC = 14, 4 N ]
b) Wie groß ist die Gravitationskraft zwischen den beiden Protonen (Masse eines Protons 1, 67 · 10−27 kg)?
[FG = 1, 16 · 10−35 N ]
*) Klausuraufgabe aus der Nachholklausur zur Vorlesung „Physik für Pharmazeuten“ im Sommersemester 2009