Aufgabe 1: Navier-Stokes-Gleichungen

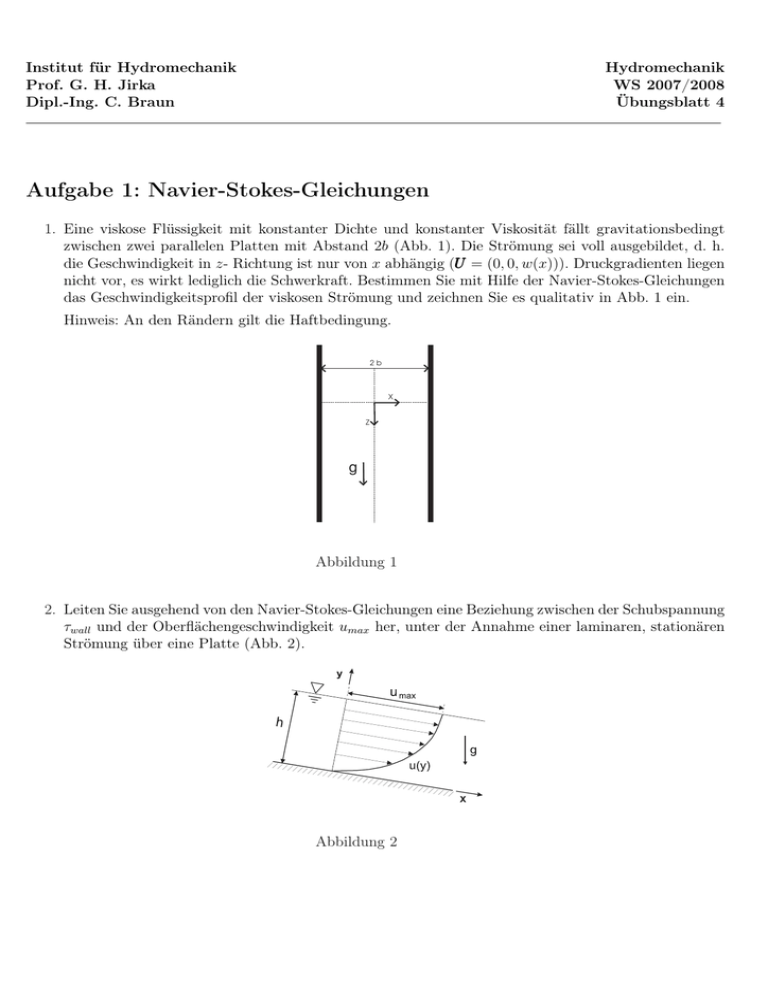
Institut für Hydromechanik
Prof. G. H. Jirka
Dipl.-Ing. C. Braun
Hydromechanik
WS 2007/2008
Übungsblatt 4
Aufgabe 1: Navier-Stokes-Gleichungen
1. Eine viskose Flüssigkeit mit konstanter Dichte und konstanter Viskosität fällt gravitationsbedingt
zwischen zwei parallelen Platten mit Abstand 2b (Abb. 1). Die Strömung sei voll ausgebildet, d. h.
U = (0, 0, w(x))). Druckgradienten liegen
die Geschwindigkeit in z- Richtung ist nur von x abhängig (U
nicht vor, es wirkt lediglich die Schwerkraft. Bestimmen Sie mit Hilfe der Navier-Stokes-Gleichungen
das Geschwindigkeitsprofil der viskosen Strömung und zeichnen Sie es qualitativ in Abb. 1 ein.
Hinweis: An den Rändern gilt die Haftbedingung.
2b
X
Z
g
Abbildung 1
2. Leiten Sie ausgehend von den Navier-Stokes-Gleichungen eine Beziehung zwischen der Schubspannung
τwall und der Oberflächengeschwindigkeit umax her, unter der Annahme einer laminaren, stationären
Strömung über eine Platte (Abb. 2).
Abbildung 2
Aufgabe 2: Impulsungleichförmigkeitsfaktor
Gegeben ist die laminare Strömung zwischen zwei Platten mit der Geschwindigkeitsverteilung (s. Übungsblatt 3, Aufg. 2.1):
Ã
µ
¶
µ
¶2 !
z
H
H
u(z)
U =
; mit u(z) = umax · 1 −
≤z≤
; für −
0
H/2
2
2
1. Bestimmen Sie den Impulsungleichförmigkeitsfaktor β, mit
Z
1
β=
(u(z)/u)2 dA .
A
A
2. Was beschreibt dieser Impulsungleichfömigkeitsfaktor und wofür wird er verwendet?
Aufgabe 3 : Impulsgleichung: Anwendungen
1. Ein horizontal liegender rechteckiger Wasserstrahl mit Querschnittsfläche A trifft mit der Geschwindigkeit V1 tangential auf eine Turbinenschaufel und wird von dieser abgelenkt.
(a) Bestimmen Sie die von dem Strahl auf die ruhende Schaufel ausgeübte Kraft Sr .
(b) Ermittel Sie für den Fall, dass die Schaufel sich mit der Geschwindigkeit V0 in Richtung des
auftreffenden Wasserstrahls bewegt, die vom Strahl auf die Schaufel wirkende Kraft Sb .
(c) Geben Sie für den Fall der bewegten Schaufel unter b) die Absolutgeschwindigkeit des Wassers
im Punkt 2 nach Größe und Richtung an.
Gegeben:
Querschnittsfläche A = 10 cm2 , Umlenkwinkel α = 150 , Wasserdichte ρ = 1000 kg/m3 ,
Strahlgeschwindigkeit V1 = 30 m/s, Schaufelgeschwindigkeit V0 = 20 m/s
Abbildung 3
2. Die Fläche in Abb. 4 teilt den auftreffenden Wasserstrahl so, dass in beide Richtungen dieselbe
Wassermenge abfließt.
Bestimmen Sie für die Zuflussgeschwindigkeit V die beiden Komponenten Fx und Fy der an der Fläche
erforderlichen Haltekraft.
Gegeben:
Volumenfluß im Zufluß: Q = 0, 1 m3 /s,
Wasserdichte: ρ = 1000 kg/m3
Zuflußgeschwindigkeit: V = 15 m/s,
Abbildung 4
3. Durch die in Abb. 5 dargestellte „Doppeldüse“ wird Wasser mit einem Durchfluss von Q = 0, 5 m3 /s
in die Atmosphäre eingeleitet. Wie groß muss die x-Komponente der Kraft sein, die auf die Schraubflansche wirkt, um die Düse in ihrer Position zu halten, wenn die Düse in einer Horizontalebene
liegt?
Hinweis: Die Strömung kann als rotationsfrei angenommen werden.
y
10 cm
12 cm
x
30°
30
cm
Abbildung 5
4. Ein Mann versucht mit Hilfe eines Brettes auf einer Fontaine zu reiten (Abb. 4). Seine Masse (gemeinsam mit dem Brett) beträgt m. Der Durchmesser des Austrittrohres sei d. Der Strahl tritt mit
der Geschwindigkeit v1 aus. Die Reibung soll vernachlässigt werden.
(a) In welcher Höhe h wird die Person gehalten?
(b) Was passiert, wenn bei gleicher Geschwindigkeit v1 der Durchmesser d nur 0, 1 m beträgt?
(c) Wie groß ist in beiden Fällen die Reynoldszahl?
(d) Wie hoch ist der Strahl wenn der Mann auf seinem Brett ausrutscht?
Gegeben:
d = 0, 3 m,
v1 = 10 m/s, m = 80 kg,
ρ = 1000 kg/m3
Abbildung 6
5. In die Druckrohrleitung eines Wasserkraftwerkes ist eine Rohrverzweigung mit Abzweigwinkel
α = 30◦ einzubauen (siehe Abb. 7). Im Querschnitt 1 (d1 = 1, 3 m) herrscht ein Druck von
p1 = 55 kN/m2 und eine Geschwindigkeit von v1 = 3, 8 m/s. Im Querschnitt 3 ( d3 = 0, 5 m),
herrscht ein Druck von p3 = 32 kN/m2 . Dem Verzweigungsstück entspricht eine Gewichtskraft von
G = 22 kN und ein Innenvolumen von V = 9 m3 . Berechnen Sie für z = 2 m
a) den Druck p2 und den Durchfluss Q2 im Querschnitt 2 für d2 = 1, 3 m,
b) den Durchfluss Q3 im Querschnitt 3,
c) die Kraft auf das Auflager.
Hinweis:
Nehmen Sie konstante Geschwindigkeiten in den jeweiligen Querschnitten an, wie auch eine verlustfreie und stationäre Strömung eines inkompressiblen Fluids. Die Gravitation wirkt entgegen der zKoordinate.
z
d1
x
v1 p1
Rohrverzweigung
αα
z
Auflager
v3
p3
v2 p2
d2
d3
Abbildung 7
6. In Abb. 8 ist eine horizontal liegende Düse dargestellt die mit Wassser der Dichte ρ = 998 kg/m3
durchströmt wird. Am Querschnitt 1 (D1 = 80 mm) wird der Überdruck von p1 = 3 bar gemessen.
Am Querschnitt 2 (D2 = 40 mm) verlässt das Wasser die Düse in Form eines horizontalen Freistrahls
mit Kreisquerschnitt, der später von einer mit ϕ = 35◦ geneigten Platte umgelenkt wird. Die Strömungsgeschwindigkeit kann als gleichförmig über den Strahlquerschnitt angenommen werden. Die
Reibung zwischen Strahl und Platte sowie in der Düse kann vernachlässigt werden.
a) Bestimmen Sie den Durchfluss durch die Düse.
b) Zeichnen Sie in Abb. 8 ein Kontrollvolumen zur Bestimmung der horizontalen Haltekraft an der
Schraubverbindung (Querschnitt 1) ein.
c) Bestimmen Sie die Größe und Wirkungsrichtung der horizontalen Haltekraft an der Schraubverbindung (Querschnitt 1).
d) Zeichnen Sie in die Abb. 8 ein Kontrollvolumen zur Bestimmung der Kräfte auf die Umlenkplatte
ein.
e) Bestimmen Sie die Abflüsse in den Querschnitten 3 und 4 nach der Umlenkung des Freistrahles.
f) Bestimmen Sie den Kraftangriffspunkt, die Größe und Wirkungsrichtung der Kraft, mit der die
Umlenkeinrichtung gehalten werden muss.
Q4
Querschnitt 2
Querschnitt 1
Spritzdüse
V2
V1
D1 =60mm
p1=4bar
j
D2 =20mm
Q3
Abbildung 8
7. Von einer Talsperre führt eine Druckrohrleitung über einen Steilhang zum Maschinenhaus, wo sie
zur Versorgung einer Freistrahlturbine mit einer Düse (D2 = 0, 2 m) endet. Das Zuleitungsrohr
(D1 = 0, 8 m) zur Düse ist wenige Meter vor dem Strahlaustritt verankert. Am Querschnitt 1 ist ein
Dehnungsstück eingebaut, sodass weder Kräfte noch Momente aufgenommen werden können (siehe
Abb. 9). Der Durchfluss durch die Rohrleitung sei Q = 2 m3 /s und das Innenvolumen des betrachteten
Kniestückes (von Querschnitt 1 bis zum Austritt) sei V = 15, 3 m3 . Der Abstand zwischen der
Querschnittstelle 1 und der Knickstelle beträgt L = 20 m, der Winkel α beträgt 30° (siehe Abb. 9).
• Wie groß ist die Druckhöhe an der Stelle 1?
• Wie groß ist die resultierende Kraft F auf die Verankerung nach Größe und Richtung (Φ)?
Hinweise:
Alle Verluste können hier vernachlässigt werden.
1
D1
L
α
φ
D2
F
Verankerung
Abbildung 9
6