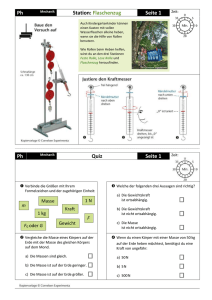
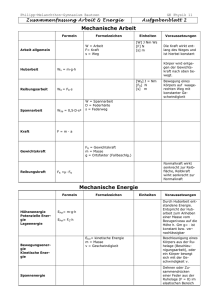
1.1.2.4 Mechanik
Werbung

Freiwillige Feuerwehr Rosenheim Mechanik Hans Meyrl Stadt Rosenheim Sachgebiet III/323 Brand- und Katastrophenschutz, ILS Grundlagen Die Mechanik ist ein Teilgebiet der Physik und befasst sich mit der Bewegung von Körpern und der Einwirkung von Kräften. Die Grundgesetze der Mechanik wurden von Galileo Galilei (1564 – 1642) und Isaac Newton (1663 – 1727) entwickelt. Arten der Mechanik Mechanik der festen Körper Mechanik der Flüssigkeiten Mechanik der Gase Basiseinheiten System internationaler Einheiten = SI-Einheiten Größe Länge Einheitsname Meter Einheitszeichen m Masse Kilogramm kg Zeit Sekunde s el. Stromstärke Ampere A Temperatur Kelvin K Stoffmenge Mol mol Lichtstärke Candela cd Abgeleitete Einheiten Größe Formelzeichen Name Einheitenzeichen Basiseinheit Temperatur C Celsius Dichte ρ Druck P Fallbeschleunigung g Gewichtskraft G Newton N kg x m x s-2 Fläche A Quadratmeter m² m² Volumen V Kubikmeter m³ m³ Pascal °C T –273,15 kg/m³ kg/dm³ Pa kg x m-1 x s-2 m/s² Vorsilben von Zahlen Vielfache von Einheiten Vorsatz Zeichen Faktor Zahl Deka da 101 10 Hekto h 102 100 Kilo k 103 1.000 Mega M 106 1.000.000 Giga G 109 1.000.000.000 Tera T 1012 1.000.000.000.000 Vorsilben von Zahlen Teile von Einheiten Vorsatz Dezi Zenti Milli Mikro Nano Pico Zeichen d c m µ n p Faktor 10-1 10-2 10-3 10-6 10-9 10-12 0,1 = 1/10 = 10-1 Zahl 0,1 0,01 0,001 0,000.001 0,000.000.001 0,000.000.000.001 Maßeinheiten Länge (L) 1m Meter 1 m = 10 dm, 1 dm = 10 cm, 1 cm = 10 mm Fläche (A) =l*b 1 m² Quadratmeter 1 m² = 100 dm², 1 dm² = 100 cm², 1 cm² = 100 mm² 100 m² = 1 Ar (a), 100 a = 1 Hektar (h) 100 h = 1 Quadratkilometer (km²) = 106 m² Volumen (V) = l * b * h = A * h = 1 m³ Kubikmeter 1 m³ = 1000 dm³, 1 dm³ = 1000 cm³ 1 cm ³ = 1000 mm³,1 Liter = 1000 cm³ = 1dm³ Maßeinheiten Masse (m) 1 kg Masse = Volumen * Dichte Kilogramm m=V*ρ In Paris aufbewahrter Platin-Iridium-Zylinder mit einem Durchmesser von 39 mm und einer Höhe von 39 mm = 1 dm³ Wasser bei 4°C 1 Tonne (t)= 1000 kg, 1 Kilogramm (kg)= 1000 g Dichte (ρ = roh) kg/dm³ Masse ρ= t = Volumen kg = m³ g = dm³ cm³ Formeln umstellen 12 12 = 3 x 4 12 3= 4= 4 m m=V x ρ 3 m ρ= V= ρ V (*) m (*) = V (:) ρ (:) V ρ (*) Formeln umstellen 7=4+3 4=7-3 3=7-4 A=B+C B=A-C C=A-B +A +B +C = +A +C -B = Beispiel 1 Ein Ziegelstein von 24 cm Länge, 11,5 cm Breite und 7,1 cm Höhe hat eine Masse von 3,1 kg. Frage: Wie groß ist seine Dichte ρ? m V= l*b*h = 24 cm * 11,5 cm * 7,1 cm = ρ= V = 1960 cm³ = 1,960 dm³ 3,1 kg ρ= kg = 1,5816 1,96 dm³ kg = 1,58 dm3 dm³ Beispiel 2 Welche Grundfläche muss in einem Wohnhaus für die Lagerung von 6.000 kg Koks vorgesehen werden? Die mittlere Schütthöhe soll 1,2 m betragen. ρ = 0,6 kg/dm³ m V= kg * dm³ kg = = ρ = dm³ kg kg/dm³ m*m*m V V=A*h = m² = A= h m Beispiel 2 - Berechnung m V= 6000 kg = ρ 6000 kg * dm³ = 0,6 kg/dm³ = 10.000 dm³ 0,6 kg = 10.000 dm³ = 10 m³ V 10 m³ A= = = 8,333 m² = 8,3 m² h 1,2 m Beispiel 3 Berechnen Sie die Masse eines gleichschenkeligen, Scharfkantigen Winkelstahls mit dem in der Abb. gegebenen Querschnitt, und einer Länge von l = 2,2m, ρ = 7,8 kg/dm³ V = A * l (h) m=V*ρ A = l1*b1 + l2*b2 Beispiel 3 - Berechnung A = dm * dm + dm * dm = dm² A = l1*b1 + l2*b2 A = 0,5 * 0,05 + 0,45 * 0,05 = V=A*l 0,025 + 0,0225 = 0,0475 dm² V = dm² * dm = dm³ V = 0,0475 * 22 = 1,045 dm³ m=V*ρ dm³ * kg m= = kg dm³ m = 1,045 * 7,8 = 8,151 m = 8,15 kg Kräfte Im täglichen Leben spricht man in vielen Wortverbindungen von Kräften: Zugkraft, Druckkraft, mit voller Kraft gegen eine Mauer fahren usw. Obwohl man sich unter Kraft etwas Bestimmtes vorstellt, kann man Kräfte nicht sehen, zu sehen ist nur beispielsweise die Verformung durch Druck, oder die Bewegung eines Gegenstandes durch Zug. Kräfte Jeder Gegenstand und jede Materienmenge unserer Umwelt werden von der Erde angezogen. Die Größe dieser Erdahnzeihungskraft wird im täglichen Leben ebenso wie die Materiemenge als Gewicht bezeichnet. Um sie deutlicher als Kraft zu kennzeichnen, verwendet die Physik die Bezeichnung Gewichtskraft FG. Sie ist im wesentlichen die von der Erde verursachte Kraft, die jeden Körper in Richtung Erdmittelpunkt zu ziehen sucht. Kräfte Gewichtskraft = Masse * Fallbeschleunigung FG = m * g [FG] = N kg * m m = 9,81 N = 9,81 FG = 1 kg * 9,81 s² s² Parallele Kräfte Kräfte im selben Angriffspunkt Fges = F1 + F2 F1 F2 F1 + F2 Fges • Wirken zwei oder mehr parallele Kräfte auf einen Punkt, so können sie sowohl rechnerisch wie auch zeichnerisch zusammengesetzt oder voneinander abgezogen werden. Parallele Kräfte F1 F2 F3 Fges = F1 + F3 – F2 F1 F3 Fges F2 Kräfte in einem bestimmten Winkel Für einen Fall dieser Art wird das Kräfteparallelogramm oder das Krafteck angewendet. Mit beiden lassen sich zwei oder mehrere Kräfte zu einer Ersatzkraft oder Resultierenden zusammenfassen. Zur Ermittlung benötigt man ein Zeichendreieck und ein Lineal. Kräfte in einem bestimmten Winkel • Kräfteparallelogramm F1 FR F2 F1 = 80 kN, F2 = 110 kN → FR = 170 kN Kräfte in einem bestimmten Winkel Zeichnerische Lösung F1 FR F2 Kräfte in einem bestimmten Winkel Mehrere nicht parallele Kräfte F1,2 = Resultierende aus F1 und F2 F1 F1,2 FR F3 F2 FR = Resultierende aus F1,2 und F3 Kräfte in einem bestimmten Winkel Krafteck F2 F1 F3 FR F3 F2 Kräfte in einem bestimmten Winkel Beim Krafteck wird die Konstruktion einfacher und F1 übersichtlicher, wenn man beachtet, dass der gestrichelte Linienzug, der vom Angriffspunkt A über B A und C zum Endpunkt D der Resultierenden führt. F 3 B F2 C F3 FR F2 D Kräfte in einem bestimmten Winkel Schriftliche Berechnung der resultierenden Kraft FR F1 cos ά F2 FR = F1² + F2² + 2 * F1 * F2 * cos ά Heben von Lasten F0,84 F0,84 F1,0 F1,0 F0,5 F0,5 FR = 1 70° FG= 1 FG 120° FG • Merke: Ab einem Spreizwinkel von 120°entspricht di e Last in jedem Seil der tatsächlichen Last. Hebelgesetz Brechstange, Hebbaum, Drehleiter oder Kran sind Geräte aus der Feuerwehrpraxis, die als wichtigstes Prinzip die Grundsätze des Hebelgesetzes beinhalten. Last * Lastarm = Kraft * Kraftarm F1 * l1 = F2 * l2 • Was man an Kraft spart muss man an Weg zurücklegen. Hebelgesetz einseitiger Hebel zweiseitiger Hebel Winkelhebel • Jede Kraft die durch den Drehpunkt geht, versucht den Hebel in Drehung zu versetzen. Hebelgesetz F1 * l1 = F2 * l2 l1 l2 F2 F1 F1 l2 = F2 l1 Berechnung 1 F1 = ? F2 l2 F2 = 500 N, l2 = 50 cm, l1 = 160 cm l1 F2 * l2 F1 * l1 = F2 * l2 F1 = l1 500 N * 50 cm F1 = = 156,25 N 160 cm Berechnung 2 F1 F2 • F1 = 300 N, l2 = 10cm F2 = 1,5 kN l2 F2 = 1500 N l1 = ? F2 * l2 F1 * l1 = F2 * l2 l1 = F1 1500 N * 10 cm l1 = = 300 N 50 cm Berechnung 3 F1 F2 = ? • F1 = 500 N, l1 = 2,5 m l2 = 20 cm l2 l1 F1 * l1 F1 * l1 = F2 * l2 F2 = l2 500 N * 250 cm F2 = = 20 cm 6250 N = 6,250 kN Berechnung 4 A S FG l/2 FA x1 F l/2 x2 l F FG l/2 FA x1 l l/2 x2 • Berechnen Sie die Auflagekraft in in den Punkten A und B. FB Wenn F = 20 kN, l = 5 m FG = 150 N und x2 = 1,25 m ist. B • Um die Auflagekraft in Punkt A zu finden, fasst man das ganze Brett mit der Last F als Hebel mit dem Drehpunkt B auf. B Berechnung 4 F A FG l/2 l/2 x2 x1 l FB * l = FG * l/2 + F *x1 F1 * l1 = F2 * l2 FG * l FB = F * x1 + 2*l FB • Um die Auflagekraft in Punkt B zu finden, fasst man das ganze Brett mit der Last F als Hebel mit dem Drehpunkt A auf. = l FG F * x1 + 2 l Berechnung 4 FG * l FA = + 2*l = l 150 N FA = FG F * x2 + 2 l F * x2 20000 N * 1,25 m + 2 75 N + 5000 N = = 75 N + 4000 N * 1,25 5m 5.075 N Berechnung 4 FG * l FB = F * x1 + 2*l l 150 N FB = = FG F * x1 + 2 l 20000 N * 3,75 m + 2 = 75 N + 4000 N * 3,75 5m 75 N + 15000 N = 15.075 N Schlussfolgerung A S FG l/2 FA x1 F l/2 x2 B FA + FB = F + FG FB l 15.075 N + 5.075 N = 20.000 N + 150 N 20.150 N = 20.150 N ∑FR = ∑FL Die Summe aller rechtsdrehenden Kräfte muss gleich der Summe aller linksdrehenden Kräfte sein. Berechnung 5 Bei einem Kran haben die einzelnen Teile die angegebenen Gewichtskräfte und die angegebenen waagerechten Abstände. Berechnen Sie die Auflagekräfte in den Achsen A und B . FA F4 F3 F2 F1 FB F1 = 60 kN, F2 = 27 kN F3= 8 kN, F4 = 20 kN Berechnung 5 Berechnung der Kräfte in Bezug zur Drehachse „A“ l FA F4 F3 FB l3 l2 F2 F1 l4 FB * l = F1 * l1 + F2 * l2 – F3 *l3 – F4 * l4 F1 * l1 + F2 * l2 – F3 * l3 – F4 * l4 FB = l l1 Berechnung 5 60 kN * 1,6m + 27 kN * 1 m – 8 kN * 0,8 m – 20 kN * 3 m FB = 2m 60 kN * 1,6 + 27 kN * 1 – 8 kN * 0,8 – 20 kN * 3 FB = 2 96 kN + 27 kN – 6,4 kN – 60 kN FB = 123 kN – 66,4 kN = 2 = 28,3 kN = 2 Berechnung 5 Berechnung der Kräfte in Bezug zur Drehachse „B“ l FA FB F4 F3 l3 F2 F1 l4 FA * l = F1 * l1 + F2 * l2 + F3 *l3 + F4 * l4 F1 * l1 + F2 * l2 + F3 * l3 + F4 * l4 FA = l l2 l1 Berechnung 5 60 kN * 0,4 m + 27 kN * 1 m + 8 kN * 2,8 m + 20 kN * 5 m FA = 2m 60 kN * 0,4 + 27 kN * 1 + 8 kN *2,8 + 20 kN * 5 FA = 2 24 kN + 27 kN + 22,4 kN + 100 kN FA = 173,4 kN = 2 = 86,7 kN = 2 Feste Rolle • Eine feste Rolle kann man als einen gleicharmigen Hebel auffassen, so dass die Kräfte in beiden Seiten gleich sind. Feste Rolle d F1 * F1 F2 d = F2 * 2 2 F1 = F2 SZug = SHub • Ein feste Rolle verwendet man zum umlenken von Kräften und bezeichnet sie als Umlenkrolle. Lose Rolle • Befestigt man eine Rolle an der Last, das eine Ende des Seils an einem Festpunkt, das andere an der Seilwinde, so spricht man von einer losen Rolle. • Das Seil vom Festpunk bis zur Rolle bewegt sich nicht. Lose Rolle l1 = d F1 * l1 = F2 * l2 d F1 F1 * d = F2 * A 2 F2 l2 = d/2 F2 * d F1 = F2 F1 = 2*d 2 Flaschenzug • Der einfachste Flaschenzug ist der Faktorenflaschenzug. Er besteht aus einer oder mehreren festen und losen Rollen. Dabei werden die festen und die losen Rollen je für sich auf einer Achse in einem gabelförmigen Lager, einer so genannten „Flasche“, befestigt. Flaschenzug • Bei gewöhnlicher Bauart sind es gleichviel feste und lose Rollen (in der Abb. je zwei), und die Zahl der verbindenden Seilstücke zwischen den beiden Flaschen ist ebenso groß wie die Gesamtzahl der Rollen. Die Gewichtskraft der Last FHub verteilt sich gleichmäßig auf alle vier Seilstücke. Flaschenzug • Deshalb ist die zum Gleichgewicht notwendige Kraft FZug am Ende des freien Seilendes bei n Trag-seilen nur der n-te Teil von der Gewichtskraft der Last. Gewichtskraft der Last Zugkraft = Anzahl der Tragseile Flaschenzug F2(Hub) F1(Zug) = n • Bei vier Rollen ist aber der Kraftweg viermal größer als der Lastweg. Was an Kraft gewonnen wird, geht an Weg verloren. Kraftweg = Lastweg * Anzahl der Tragseile s1(Zug) = s2(Hub) * n Berechnung 1 Ein Faktorenflaschenzug mit vier Tragseilen dient zum hochheben einer Last von der Gewichtskraft 24 kN. a) Wie groß ist die erforderliche Zugkraft bei Vernachlässigung der Reibungsverluste? b) Welcher Zugweg muss zurückgelegt werden, wenn die Last 1,8 m hoch gehoben werden soll? a) = F1(Zug) = b) 24 kN F2(Hub) n s1(Zug) = s2(Hub) * n = 6 kN 4 s1 = 1,8 m * 4 = 7,2 m Berechnung 2 1 2 Z 16 = max. 16 kN a) Welche Kräfte wirken in den einzelnen Seilabschnitten? b) Welche Masse m kann mit einem Mehrzweckzug Z 16 in der dargestellten Anordnung gezogen werden? c) Welche Kräfte muss der Festpunkt 1 und 2 aufnehmen? Berechnung 2 1 Z 16 = max 16 kN 2 a) Seil 1 = 16 kN, Seil 2 = 16 kN, Seil 3 = 16 kN b) F2(Hub) F1(Zug) = F2(Hub) = F1(Zug) * n = 16 kN * 3 = 48 kN n c) F2(Fp 1) = F1(Zug) * n = 16 kN * 2 = 32 kN F2(Fp 2) = F1(Zug) * n = 16 kN * 1 = 16 kN Berechnung 3 F3 • Die Seilwinde des RW 2 hat eine Zugkraft von F1 = 60 kN F2 F1 a) Welche maximale Masse kann das Fahrzeug F2 haben, damit es, in der oben dargestellten Situation, geborgen werden kann? b) Welche Kraft wirkt am Baum (Festpunkt F3)? Berechnung 3 a) F = F * n = 60 kN * 2 = 120 kN 2 1 F F=m*g m= g 120000 kg * m *s² m= 9,81 m * s² F2 m = 12.234,4 kg b) F3 = F1 * n = 60 kN * 3 = 180 kN F3 F1 F1 = 60 kN Druck Als Druck bezeichnet man das Ergebnis einer Teilung einer Kraft und einer Fläche, auf die diese Kraft senkrecht zur Fläche wirkt. Es gilt folgender Zusammenhang: F Druck = Kraft : Fläche p= A Druck Die Einheit für den Druck ist das Pascal (Pa) und das Bar (bar). 1 Pa ist gleich dem auf eine Fläche gleichmäßig wirkende Druck, bei dem senkrecht auf die Fläche 1 m² die Kraft 1 N ausgeübt wird. Druck kg * m N =1 1 Pa = 1 m² kg = 1 m * m * s² m * s² 1 bar = 1 * 105 Pa = 100.000 Pa 1 Pa = 1 * 10-5 bar = 0,00001 bar Berechnung 1 Ein Balken von 3,2 m Länge, 10 cm Breite und 14 cm Höhe (ρ = 0,75 kg/dm³) liegt an beiden Enden 8 cm auf seinen Unterstützungsmauern auf. m Berechnen Sie die Flächenpressung. ρ V m=V*ρ= l*b*h*ρ 32 dm * 1 dm * 1,4 dm * 0,75 kg m= dm³ FG = m * g = = 33,6 kg 33,6 kg * 9,81 m = 329,616 N s² Berechnung 1 A=l*b*2= F p= 0,1 m * 0,08 m * 2 = 0,016 m² 329,616 N = A = 20601 Pa 0,016 m² p = 20601 Pa *10-5 = 0,206 bar Hydrostatischer Druck • Wird in einem geschlossenen System auf eine Flüssigkeit Druck ausgeübt, pflanzt sich dieser aufgrund der Verschiebbarkeit der Flüssigkeiten nach allen Seiten gleichmäßig fort. Der aufgebrachte Druck innerhalb des Systems ist dann überall gleich. F • Dies ist die Grundlage für das Prinzip einer hydraulischen Presse. Hydrostatischer Druck F1 F2 F1 = F2 • Weist das Ende eines geschlossenen Systems die gleiche Größe der Fläche auf, so herrscht auch hier die gleiche Kraft. Hydrostatischer Druck Wird am Ende eines geschlossenen Systems die Druck beaufschlagte Fläche vergrößert, ergibt sich daraus auch eine Vergrößerung der Kraft. Hydrostatischer Druck F2 F1 A1 A2 Das heißt, bei einer hydraulischen Presse wird mit einer kleinen Kraft F1 die auf einen kleinen Kolben mit der Druckfläche A1 wirkt, eine große Kraft F2 an einem Kolben mit der großen Druckfläche A2 erzeugt. Hydrostatischer Druck F2 F1 A1 A2 • Das Übersetzungsverhältnis der Kräfte F1 zu F2 ist gleich dem Verhältnis der Flächen A1 zu A2, da der Druck überall gleich ist. Durch den Hubweg des kleinen Kolbens wird eine bestimmte Menge Flüssigkeit verschoben, die wiederum den großen Kolben um ein entsprechend kleineren Hubweg anhebt. Hydrostatischer Druck F2 A2 F1 Das Übersetzungsverhältnis der Hubwege S1 zu S2 ist gleich dem Verhältnis der Flächen A2 zu A1. A1 F1 p= F2 F1 s1 = p= A1 F2 A2 A1 A2 = A2 s2 A1 Berechnung 1 Mit einem Hydraulikheber, der einen Kraftkolben von A1 = 3 cm²hat, soll ein Kraftfahrzeug mit der Masse m = 1,5 t um s2 = 20 cm angehoben werden. Die Fläche des Hubkolbens A2 = 300 cm². Berechnen Sie die notwendige Kraft am Kraftkolben F1 den Weg s1 am Kraftkolben und den Druck der Flüssigkeit. a) F2 = m * g = 1500 kg * 9,81 m/s² = F1 F2 = A1 F2 * A1 F1 = A2 A2 14715 N 14715 N * 3 cm² = 147,15 N = 300 cm² Berechnung 1 b) s1 A2 = s2 A2 * s2 s1 = A1 300 cm² * 20 cm = = A1 3 cm² s1 = 2000 cm c) p= = 490500 Pa = 490500 = A1 N 147,15 N F1 0,0003 m² 1 Pa = 1 * 10-5 bar m² 490500 * 0,00001 = 4,905 bar Berechnung 1 1 Pa = 1 * 10-5 bar 490500 Pa = 490500 * 10-5 = 490500 * 0,00001 = 4,905 bar Noch Fragen ?