Loesung 3. Probe

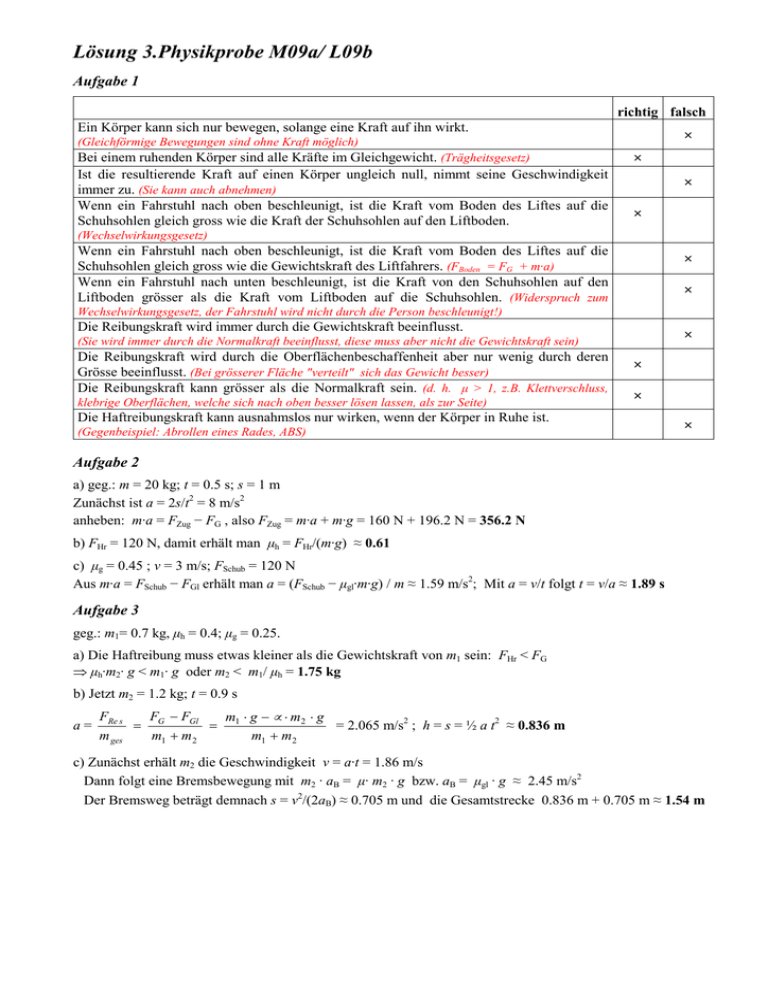
Lösung 3.Physikprobe M09a/ L09b
Aufgabe 1
richtig falsch
Ein Körper kann sich nur bewegen, solange eine Kraft auf ihn wirkt.
×
(Gleichförmige Bewegungen sind ohne Kraft möglich)
Bei einem ruhenden Körper sind alle Kräfte im Gleichgewicht. (Trägheitsgesetz)
Ist die resultierende Kraft auf einen Körper ungleich null, nimmt seine Geschwindigkeit
immer zu. (Sie kann auch abnehmen)
Wenn ein Fahrstuhl nach oben beschleunigt, ist die Kraft vom Boden des Liftes auf die
Schuhsohlen gleich gross wie die Kraft der Schuhsohlen auf den Liftboden.
×
×
×
(Wechselwirkungsgesetz)
Wenn ein Fahrstuhl nach oben beschleunigt, ist die Kraft vom Boden des Liftes auf die
Schuhsohlen gleich gross wie die Gewichtskraft des Liftfahrers. (FBoden = FG + m·a)
Wenn ein Fahrstuhl nach unten beschleunigt, ist die Kraft von den Schuhsohlen auf den
Liftboden grösser als die Kraft vom Liftboden auf die Schuhsohlen. (Widerspruch zum
×
×
Wechselwirkungsgesetz, der Fahrstuhl wird nicht durch die Person beschleunigt!)
Die Reibungskraft wird immer durch die Gewichtskraft beeinflusst.
×
(Sie wird immer durch die Normalkraft beeinflusst, diese muss aber nicht die Gewichtskraft sein)
Die Reibungskraft wird durch die Oberflächenbeschaffenheit aber nur wenig durch deren
Grösse beeinflusst. (Bei grösserer Fläche "verteilt" sich das Gewicht besser)
Die Reibungskraft kann grösser als die Normalkraft sein. (d. h. µ > 1, z.B. Klettverschluss,
klebrige Oberflächen, welche sich nach oben besser lösen lassen, als zur Seite)
×
×
Die Haftreibungskraft kann ausnahmslos nur wirken, wenn der Körper in Ruhe ist.
(Gegenbeispiel: Abrollen eines Rades, ABS)
×
Aufgabe 2
a) geg.: m = 20 kg; t = 0.5 s; s = 1 m
Zunächst ist a = 2s/t2 = 8 m/s2
anheben: m·a = FZug − FG , also FZug = m·a + m·g = 160 N + 196.2 N = 356.2 N
b) FHr = 120 N, damit erhält man µh = FHr/(m·g) ≈ 0.61
c) µg = 0.45 ; v = 3 m/s; FSchub = 120 N
Aus m·a = FSchub − FGl erhält man a = (FSchub − µgl·m·g) / m ≈ 1.59 m/s2; Mit a = v/t folgt t = v/a ≈ 1.89 s
Aufgabe 3
geg.: m1= 0.7 kg, µh = 0.4; µg = 0.25.
a) Die Haftreibung muss etwas kleiner als die Gewichtskraft von m1 sein: FHr < FG
⇒ µh·m2· g < m1· g oder m2 < m1/ µh = 1.75 kg
b) Jetzt m2 = 1.2 kg; t = 0.9 s
a=
FRe s
F − FGl
m ⋅ g − µ ⋅ m2 ⋅ g
= G
= 1
= 2.065 m/s2 ; h = s = ½ a t2 ≈ 0.836 m
m ges
m1 + m 2
m1 + m 2
c) Zunächst erhält m2 die Geschwindigkeit v = a·t = 1.86 m/s
Dann folgt eine Bremsbewegung mit m2 · aB = µ· m2 · g bzw. aB = µgl · g ≈ 2.45 m/s2
Der Bremsweg beträgt demnach s = v2/(2aB) ≈ 0.705 m und die Gesamtstrecke 0.836 m + 0.705 m ≈ 1.54 m